弃渣场物理力学参数选择与多维度稳定性分析研究
2022-11-15温家华
王 昱,闵 丽,温家华,凌 超,方 舒
(1.国网新源控股有限公司抽水蓄能技术经济研究院,北京市 100761;2.长江勘测规划设计研究有限责任公司,湖北省武汉市 430010)
0 引言
弃渣场是水电工程固体废弃物的堆置场所,是水土流失的重点区域,也是工程安全重点关注的对象。随着生态文明建设的推进,对保护环境、控制水土流失提出了更高的要求。弃渣场既不同于堆石坝,也有别于天然边坡,对其构成材料的特殊性和复杂性往往认识不足,导致现有的计算方法和基于工程类比确定的参数可能存在较大离散性和不确定性[1]。
针对以上情况,本文通过资料收集、文献分析,开展影响弃渣体稳定的要因分析,确定不同边界条件下弃渣体的稳定状况;依据边坡变形失稳机理总结,针对不同的计算方法,提出弃渣物理力学参数选择方法。
1 典型弃渣场概况
通过对多个水电站弃渣场进行实地考察,最终确定安徽某抽水蓄能电站下水库2号弃渣场作为研究对象。主要原因是该弃渣场已临近堆渣尾声,渣场场地开阔,利于开展地质勘察工;该弃渣场局部坡面正在进行修整作业,可以作为研究分析的典型案例。
根据典型弃渣场设计专题报告及现场实际施工情况,堆渣量约为323万m3,占设计堆渣量的71.9%, 实际堆渣占地面积约为15.64hm2。典型弃渣场为特大型弃渣场,拦挡防护设施级别为3级,弃渣场防洪设计标准采用50年一遇洪水[2]。弃渣场工程防护措施包括拦挡工程、截排水工程、沉沙工程和土地整治工程。典型弃渣场全貌如图1所示。

图1 典型弃渣场全貌Figure 1 Overview of typical spoil ground
2 弃渣物理力学参数选择
为获取弃渣土体物理力学性质,分别进行了现现场试验和取样进行室内颗粒分析及模拟三轴试验、击实试验,用以获取弃渣体相应的物理力学指标,获得E-μ(B)等相关参数。现场取样5组,其中弃渣体大样4组,钻孔岩芯样1组。试验内容包括颗粒分析试验、击实试验、大型三轴试验、自然休止角试验,获得了4种渣料的级配、最大干密度、抗剪强度指标、E-μ(B)变形参数以及自然休止角等指标。4种渣料(y1~y4)和1种钻孔料(zk2)共计5种料级配曲线如图2所示。

图2 弃渣级配曲线图Figure 2 Grading curve of waste slag
2.1 刚体极限平衡法参数选取
刚体极限平衡法相关岩土物理力学参数可根据现场和室内试验成果及电站前期勘察成果,类比已收集到的类似工程确定,其中弃渣物理力学参数依据参数反演与堆渣现状坡面对比获得[3]。弃渣体为散粒物,渣体内未见连续软弱界面,厚度较小,滑动面近圆弧形,即渣体内产生圆弧滑动,截取滑坡动面最深处纵向滑面作为计算剖面。影响渣体稳定的主要因素为暴雨,本次计算采用暴雨两种工况,计算时不考虑动水压力,渣体采用饱和容重。
根据现场试验及原位测试成果,结合相关规范与经验选取,各岩性参数取值见表1,计算结果见表2。

表1 渣体各岩性计算参数取值表Table 1 Table of calculation parameters for each lithology of slag body

表2 渣体抗剪强度指标反演计算结果表Table 2 Back calculation results of slag shear strength index

续表
当稳定系数为0.9<F<1时,渣体抗剪强度取值见表3。

表3 渣体抗剪强度指标反演计算取值表Table 3 Table of the inversion calculation values of shear strength index of slag body
对于反演结果显示当黏聚力取0时,天然内摩擦角需要达到32°~36°才能满足自稳条件,这与现实最危险堆渣状况基本相符。然而该参数未考虑深层土体的固结沉降作用,仅为表层松渣,从钻孔取样结果分析,较深层土体存在明显固结作用。故在计算中内摩擦角选择比反演结果略小,考虑部分固结后的黏聚力作用,综合得到弃渣场岩土体物理力学参数建议值见表4。
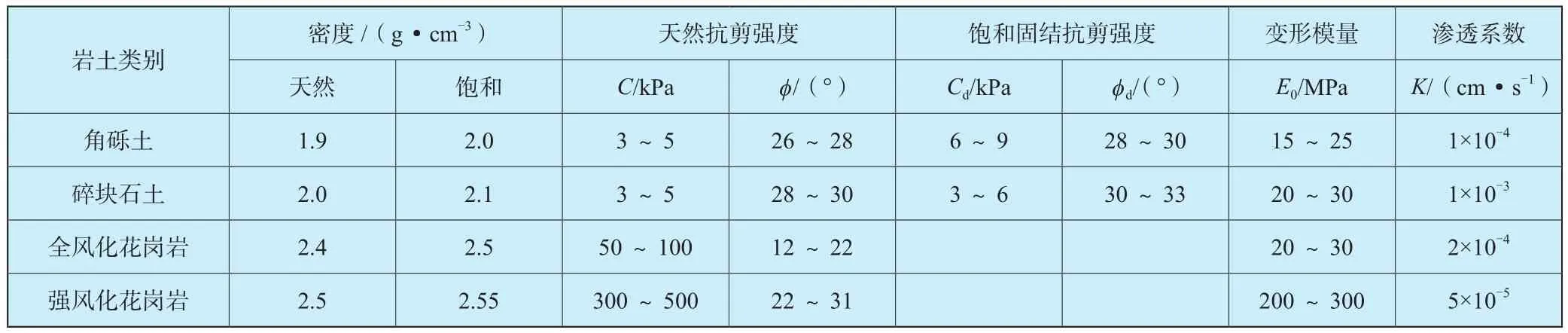
表4 弃渣场岩、土体物理力学参数建议值表Table 4 Recommended values of physical and mechanical parameters of rock and soil in waste dump
2.2 弹塑性有限元法参数选取
弹塑性有限元法相关岩土物理力学参数根据现场和室内试验成果及电站前期勘察成果,类比已收集到的类似工程确定,见表5。

表5 弃渣场岩、土体物理力学参数建议值表Table 5 Recommended values of physical and mechanical parameters of rock and soil in waste dump
3 弃渣场多维度稳定性分析
3.1 潜在破坏模式判别
典型弃渣场距离下垫面最大垂直堆渣厚度为33m,最大坡面长度为70m,单级最大坡高为31m,平均坡面坡度为1:2,下伏地基碎石土层厚约为5m,全风化层厚度局部最大为12m,平均厚度为4m;下伏基面平均坡度为15%。典型渣场堆渣厚度大,单级最大坡高大于最大允许坡高(30m),平均坡面坡度较陡,存在局部陡于1:2过渡段坡面。因此,在假设渣体为均匀介质的情况下,典型渣场坡面滑动模式主要为沿渣体内部的圆弧滑动。
下伏地基碎石土层厚度较大,分布广,但由于堆渣厚度远大于下伏地基碎石土层厚度,在堆渣过程中经历了压实固结过程,渣底坡度也较缓,因此,在正常工况下,渣体整体不会沿同地基交界面产生滑动。但在持续降雨或排水失效的条件下,由于地下水位升高,弃渣与地基交界面因淋溶效应的存在[4],产生局部强度软化,可能引起局部渣体沿底面折线产生滑动[5]。
综上所述,定量计算时需复核堆渣渣体的局部边坡稳定性和特殊条件下的整体稳定性。
3.2 弃渣体三维稳定计算分析
3.2.1 计算方法
采在松散岩土体分析中,邓肯—张E-B双曲线模型能较好地模拟土体的变形性状。该模型的参数测定有比较成熟的经验,而且测试简单,在工程计算中得到广泛应用。弃渣场静力计算材料参数见表5。
弃渣地基岩体按线弹性材料考虑,粉沙质泥岩弹性模量E=3GPa,泊松比为0.3,密度为2.32g/cm3;砂岩弹性模量E=5GPa,泊松比为0.25,密度为2.32g/cm3。
3.2.2 计算模型
选取典型弃渣场典型剖面作为计算模拟的断面,选取的典型断面同二维计算模型相一致。模型左侧为拦渣堤,共分三级主要台阶,拦渣堤、渣体材料、覆盖层和地基均采用八节点六面体等参单元,有限元计算模型见图3。模拟弃渣过程为每5m进行一次堆填,并假设堆填过程是自渣脚往渣顶进行。
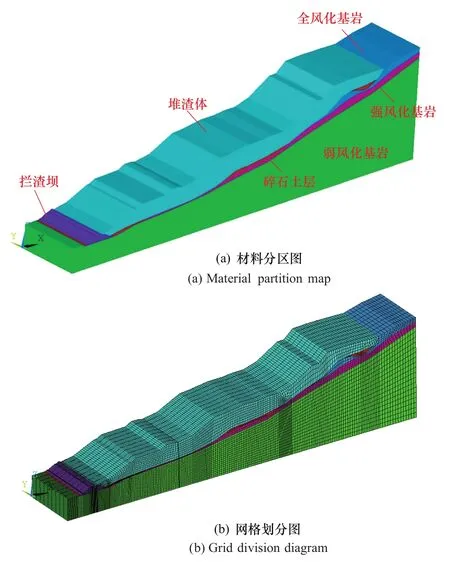
图3 典型弃渣场有限元模型Figure 3 Finite element of typical spoil ground
3.2.3 结论与分析
3.2.3.1 本构模型分析
如图4所示为计算结果,可见:

图4 典型渣场坡顶、坡底泊松比—应力水平计算图Figure 4 Poisson’s ratio stress level calculation diagram of slope top and bottom of typical slag dump
(1)对于坡体上层堆渣,实测泊松比随应力水平大致呈线性关系,初始泊松比小,且泊松比与围压关联不大,表明大变形过程主要以轴向压缩为主,侧向应变效应较弱,符合松散碎石土的变形特征,因此E-B模型能够更好地描述其泊松比—应力水平的关系。
(2)对于坡体深层堆渣,虽实测泊松比曲线随应力水平也大致呈直线型,但与围压具有联动性。同一应力水平,围压越大,泊松比越小;围压越大,初始泊松比也越小,在此情况下E-μ模型更实用。
(3)针对底部较为平缓且排水通畅的弃渣场,其沉降变形规律受深层堆渣影响较小,主要表现为浅层边坡滑动破坏,因此选择E-B模型更加合理。
3.2.3.2 变形与沉降
变形计算结果表明:正常工况下完建期渣体最大沉降为35cm,占最大堆渣厚度的1.06%,整体堆渣断面形状的设计是合理的。连续降雨工况最大沉降为86cm,占最大堆渣高度的1.15%;第三级边坡产生渣体最大水平位移为45cm,该台阶边坡同第四级边坡共同构成了该渣场轴线方向危险剖面。
3.3 弃渣体二维极限平衡法计算分析
3.3.1 计算方法
本节对典型弃渣场的典型断面采用极限平衡法中的毕肖普法进行计算复核[2]。
3.3.2 计算条件
计算荷载包括弃渣体自重、静水压力和地震力。
计算工况:正常工况为弃渣场正常运行工况,荷载组合为弃渣体自重;非正常工况I为弃渣场运行过程中遭遇降雨工况,荷载组合为弃渣体自重+静水压力。计算参数[6]见表4。
3.3.3 计算模型
计算模型如图6所示。堆渣左下角为拦渣坝,自下而上分别为一级台阶至坡顶四级台阶,堆渣坡度逐渐变陡,堆渣坡比分别为1:2.5、1:2.0、1:1.6、1:1.14,坡面堆高分别为17m、20.5m、23.5m和14.5m。
3.3.4 结果与分析
弃渣场典型剖面二维稳定计算分析分为整体稳定分析和边坡稳定分析。整体稳定分析通过指定划弧法确定渣场滑动底面,划弧为折线形,其反映了渣场场地浅层地表对渣场稳定性产生的影响;边坡稳定分析通过指定圆弧圆心和半径自动搜索最危险滑面,滑面形式为圆弧形,其反映渣体堆渣坡度、弃渣参数以及渣底局部软弱夹层对弃渣边坡稳定的影响。

图5 渣场堆渣现状计算模型(典型剖面)Figure 5 Calculation model of slag status in slag yard (typical section)
首先计算渣场进行渣场整体稳定性复核,如图6、图7所示,该典型渣场的整体稳定性良好,由于地势平坦,渣体底部软弱夹层厚度不大,整体稳定计算结果值远大于标准值。

图6 渣场整体稳定计算成果(正常工况)Figure 6 Calculation results of overall stability of slag yard (under normal conditions)

图7 渣场整体稳定计算成果(降雨工况)Figure 7 Calculation results of overall stability of slag yard (rainfall condition)
如图8、图9所示,典型渣场计算划弧出现于渣体内,说明边坡稳定控制因素为渣体自身而非地基;划弧位于三级台阶上方坡面,主要由于该位置坡面坡度较陡以及堆渣高度较高。
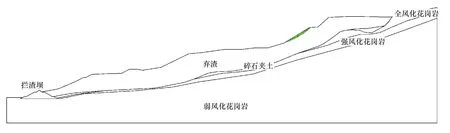
图8 渣场边坡稳定计算成果(正常工况)Figure 8 Calculation results of slope stability of slag yard (normal working condition)

图9 渣场边坡稳定计算成果(降雨工况)Figure 9 Calculation results of slope stability of slag yard (rainfall condition)
如表6所示,渣场整体稳定性均满足规范要求,但最上级边坡稳定系数小于规范允许值,因此最上级边坡后续进行了削坡整形和施加坡面防护工程措施。
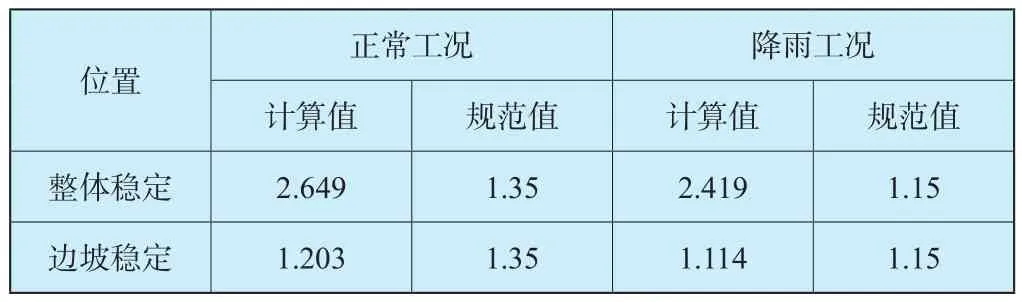
表6 典型渣场整体稳定和边坡稳定复核表Table 6 Review table for overall stability and slope stability of typical slag yard
3.4 弃渣体三维、二维稳定计算结果对比分析
选择堆渣坡比1:2.1和1:2.0的坡面对比三维计算和二维计算结果,三维稳定系数由应力水平倒数计算获得。

表7 三维和二维坡面稳定计算结果对比表Table 7 Comparison of 3D and 2D slope stability calculation results
计算结果表明,两种计算方法取得的安全系数均能满足规范要求,但采用毕肖普法比用有限元法估算的安全系数略低,说明二维刚体极限平衡法相对三维弹塑性有限元法更保守,但是三维弹塑性有限元法在真实地形条件的安全系数标准可能受多因素影响,相应标准可能更高。
5 结论
本文通过选取典型弃渣场,依据地质勘探成果和边坡变形失稳机理定性分析,针对不同的计算方法,提出弃渣物理力学参数选择方法,并对弃渣体三维、二维稳定计算结果进行了对比分析,获得以下认识:
(1)提出了一种适用于电站大型弃渣场的复杂工况多维度稳定性评价方法,提出针对抽水蓄能电站常见的大型弃渣场,常规稳定性计算分析难以满足渣体稳定性复核要求的结论,建议将有限元法同极限平衡法相结合,进行弃渣场在复杂工况下多维度稳定分析。
(2)针对弃渣场堆渣形式的特殊性和不确定性,以参数敏感性分析为基础,提出了渣体试验参数的反演和修正方法。
(3)研究提出邓肯—张E-B模型对人工堆填体多级堆渣过程模拟较E-µ模型更加合理。将三维弹塑性理论分析结果同二维刚体极限平衡(简化毕肖普法)相对比,结果表明,采用毕肖普法计算结果比有限元计算的稳定系数略低,表面二维刚体极限平衡法更偏保守。
