山区桥梁地震易损性及平均损失率分析

孙 路，李廷辉

（1.湖州职业技术学院，浙江湖州 313000；2.中国地震局工程力学研究所中国地震局地震工程与工程振动重点实验室，黑龙江哈尔滨 150080；3.湖州市绿色建筑技术重点实验室，浙江湖州 313000；4.地震灾害防治应急管理部重点实验室，黑龙江哈尔滨 150080）

引言

相对于一般的公路交通系统来讲，山区交通系统有着明显的不同，其组成大多是由桥梁与隧道构成的。我国有2/3的陆地面积为山区，由于山区地形崎岖，交通不宜普及的原因造成了经济相对落后，而随着经济发展的需要国家对山区交通系统进行了重点开发，例如西成高铁，其全长643 km，桥隧占比93%，四川汶马高速其桥隧比高达86%，而对于川藏铁路来讲，其桥隧比更是高达95.8%。我国又是一个地震多发国家，陆地面积占全世界面积的1/15，但陆地地震却占了世界的1/3。相对于平原地震，山区地震有着复杂的地形，发生地震时复杂的地形对抢险救灾极为不利，作为生命线工程，此时交通系统的破坏程度直接影响了救援的效率，因此有必要对山区桥梁的地震的抗震性能进行研究，而易损性模型不失为一种有效的手段。易损性模型建立可分为经验易损性模型与理论易损性模型。2008年的汶川8.0级地震，其受灾区有大量桥梁发生破坏，我国动员了大量地震相关人员赴实地考察，收集了宝贵的桥梁震害资料，这为建立我国山区桥梁地震易损性模型提供了基础。

经验易损性模型最早于20世纪70年代应用于结构的评估，对工程结构建立经验易损性模型主要依赖震后的结构破坏情况统计，而该过程也被称为“破坏-运动关系”，而这种关系可以通过破坏概率矩阵或易损性函数来表示。Whitman等［1］提出了一种用于组织和描述地震对建筑物造成破坏的统计数据的格式，也就是破坏概率矩阵，损伤程度由成本损失与建筑重置成本的比率来确定。美国技术应用委员会（ATC）［2-3］在编制的ATC-13规范中对破坏概率矩阵首次进行了应用。

1998年，Basoz等［4］将观察到的1989年Loma Prieta地震和1994年Northridge地震造成的桥梁损坏与地面运动、桥梁结构特征、修复成本和时间联系起来，提出了损伤状态定义；将桥梁按其结构特征分组，并进行相关研究，以获得地面运动-损伤关系和地面运动-修复成本比关系；采用Logistic回归分析得到经验易损性曲线。2000年，Shinozuka等［5］利用1995年兵库县南部地震的桥梁损伤数据建立了经验易损性曲线，利用最大似然法估计的参数，用双参数对数正态分布函数建立了易损性模型。2012年，陈立波等［6］利用汶川地震中的桥梁破坏数据，采用修正后的汶川地震衰减模型得到了桥址处的PGA，假设易损性模型符合对数正态分布，利用极大似然估计得到了全体桥梁的经验地震易损性曲线。2013年，杨帆等［7］采用层次分析的方法计算了铁路桥梁的震害指数，确定了地震破坏等级及损失比。2016年，孙路等［8］应用概率统计与定性的方法给出了桥梁震害评定指标。2017年，柳春光等［9］考虑氯离子侵蚀的影响，基于蒙塔卡罗抽样计算了一座近海桥梁的易损性。

文中依托汶川8.0级地震中收集的桥梁震害数据，按照桥梁种类分为梁桥与拱桥，采用汶川地震动衰减模型得到桥址处PGA，假设桥梁地震易损性符合双参数对数正态分布，利用极大似然估计得到每种桥梁的易损性参数，并根据《地震现场工作第4部分：灾害直接损失评估》［10］给出的损失比建立了每种类型桥梁的平均损失率模型，依据文中建立的桥梁易损性模型及平均损失率模型可以在将来发生类似地震时快速地进行地震损失评估。

1 桥梁震害统计

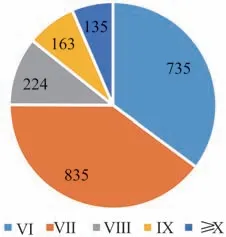
图1 调查桥梁各烈度区数量分布Fig.1 The quantity distribution of each intensity region of the investigated bridges

图2 拱桥数量分布Fig.2 Quantity distribution of arch bridges

图3 梁桥数量分布Fig.3 Quantity distribution of girder bridges

通过对四川、甘肃、陕西地震灾区的震害统计，总共得到了2 092座桥梁震害样本，各烈度下的桥梁数量如图1所示。灾区桥梁主要分为2种类型：一类为梁桥；另一类为拱桥，其他桥型较少。根据陈乐生［11］编写的《汶川地震公路震害调查》中所给出的桥梁震害等级评价体系，桥梁震害可以分为轻微破坏、中度破坏、严重破坏与毁坏。对于VI烈度区，桥梁多为轻微破坏或无破坏，共计735座。各烈度下梁桥与拱桥的数量分别如图2～图3所示。

对于VI～XI烈度区内的1 357桥梁，其各破坏等级对应的破坏数量如图4所示。对应各破坏等级的拱桥与梁桥数量分别如图5～图6所示。在汶川地震中，梁桥的震害主要表现为支座位移、主梁移位、落梁、主梁开裂、垮塌及桥墩损伤，拱桥的震害主要表现为主拱损伤、横向连接系损伤和拱上建筑震害等。

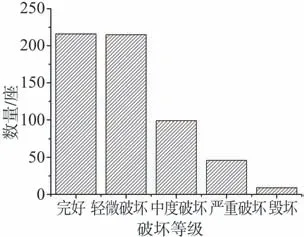
图5 VI～XI烈度区拱桥数量Fig.5 Number of arch bridges in VI～XI

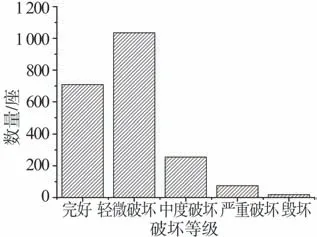
图4 VI～XI烈度区内各破坏等级桥梁数量Fig.4 Number of bridges in each failure grade in the intensity region of VI～XI

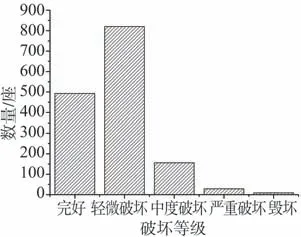
图6 VI～XI烈度区梁桥数量Fig.6 Number of girder bridges in VI～XI

2 地震动参数确定

地震动参数的选取与确定对于结构易损性模型的建立有很重要的影响，在以往的易损性研究中，许多学者倾向选择谱加速度［12-14］（Sa）作为计算结构地震易损性的地震动参数（IM），而对于桥梁工程来讲存在着无法大量获得样本基频的这一事实，因此文中选择地震峰值加速度（PGA）作为地震动参数。

邱卓［15］对汶川地震动强度指标特征进行了分析，采用统计回归的方式获得了汶川地震的地震动PGA衰减模型，回归公式如式（1）所示。

式中：c1与c2为回归系数，见表1；R为断层距（km），代表桥梁距断层破裂面的最短距离；h为震源深度影响系数，计算时可取25。经过计算发现，按照N-S方向计算得到的PGA值要相对大一些，文中选择N-S方向PGA作为桥梁桥址处的地震动强度指标。

表1 PGA衰减关系回归系数Table 1 Regression coefficient of PGA attenuation relationship

文中通过百度坐标拾取系统［16］采集桥梁桥址处的经纬度，结合程翔［17］给出的方法计算出每座桥梁距离断层破裂面的距离，再根据式（1）给出的地震动衰减模型就可求出每个桥梁桥址的PGA值。

3 桥梁易损性模型的建立

建立易损性模型的关键在于合理的选择易损性函数，要能够较好的体现地震动强度（IM）与结构破坏之间的关系。在以往的研究中，学者们选择了很多种数学模型进行易损性回归分析，如逻辑回归函数、威布尔分布函数、对数正态分布函数等。

文中选用双参数对数正态分布作为易损性函数，这一易损性函数表达式最早出现于20世纪70年代，最初是美国用来进行核电站地震风险概率评估的基本假定，后来被许多学者广泛的用在土木与地震工程领域。双参数对数正态分布函数有着数学计算简便的优点，可以将结构的实际强度与设计强度通过一个总体的安全影响因子联系起来。总体安全因子是由一系列的子安全影响因子的乘积得来，而这些子安全影响因子又都包含了不确定性。假设子安全影响因子服从对数正态分布，那么作为乘积的总体安全影响因子也同样服从对数正态分布，对应的易损性函数表达式如式（2）所示，

式中：F（a）代表结构某一损伤等级下的易损性函数；a代表PGA；Ф［］代表标准正态分布函数；c与ζ分别代表中位值与对数标准差。

为了能够求出c与ζ，文中采用独立估计的极大似然估计方法［18-19］，似然函数可以写为式（3）的形式。

式中：F［］代表结构某一损伤等级下的易损性函数，文中表现形式如式（2）所示；N代表桥梁的总数；ai代表第i座桥梁的PGA；xi代表伯努利随机事件Xi的取值，当PGA=ai时结构达到了某一损伤等级，xi取1，反之取0。依据第2节所给出的方法得到桥梁桥址处的PGA便可以建立起“名称-破坏状态-桥梁桥址处PGA”样本。

图7与图8为基于调查数据回归得到的拱桥与梁桥易损性曲线，表2为未补充数据情况下易损性函数参数估计值。从图中可以看出，在轻微破坏情况下，当PGA小于0.1 g时，曲线上升很快，这与实际情况不符，其原因为调查人员在进行实地调查时一般只关注已发生破坏的桥梁，因此忽略了大多数的完好桥梁，使回归分析中完好的桥梁数据过少，造成了在较低的PGA值，桥梁发生轻微破坏的超越概率很高。为了避免这种情况发生，应在回归分析时补充部分完好桥梁的数据（只有完好的桥梁调查人员才会忽略）。根据每一烈度每平方公里分布的桥梁数量可知，VIII以上为65 km2/座，VII度为109 km2/座，而VI度仅为420 km2/座，这也从侧面证明了部分完好桥梁在相关人员调查时确实被忽略了。可以将VIII度以上烈度区每平方公里分布的桥梁数量作为标准，分别对VII度及VI度区进行补充，补充的桥梁均为完好桥梁。

图7 拱桥地震易损性曲线（未补充数据）Fig.7 Seismic fragility curve of arch bridge（no supplementary data）

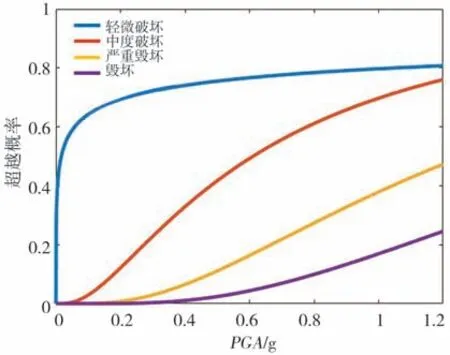
图8 梁桥地震易损性曲线（未补充数据）Fig.8 Seismic fragility curve of girder bridge（no supplementary data）

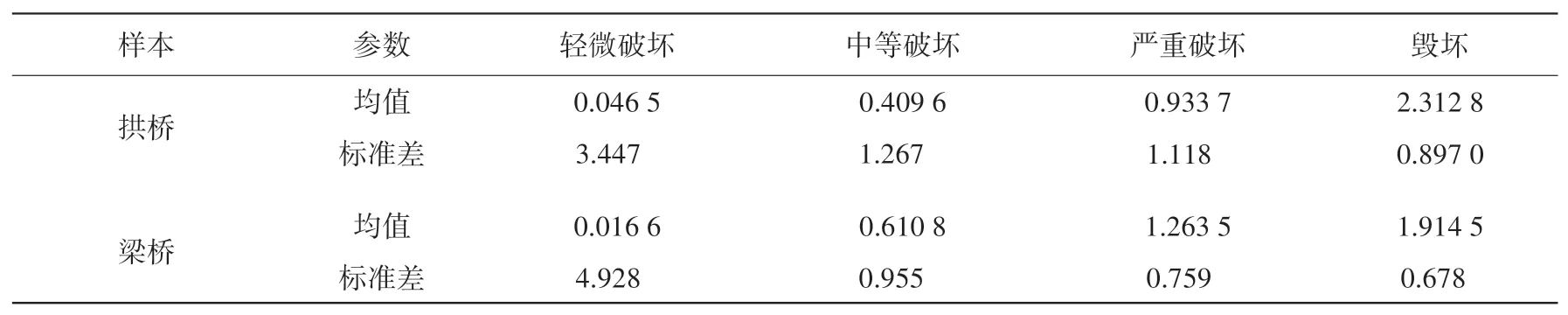
表2 易损性函数的参数估计值（未补充数据）Table 2 Estimated parameter of fragility function（no supplementary data）

图9与图10为补充数据回归得到的拱桥与梁桥易损性曲线，表3为补充数据情况下易损性函数参数估计值。从图中可以看出，经过补充数据所得到的桥梁易损性曲线在PGA较低时其超越概率明显降低，因此通过补充数据可以明显改善易损性曲线模型，使其更符合实际情况。观察表4中所列出的不同类型桥梁的地震破坏超越概率，可以发现梁桥在地震作用下发生毁坏的概率更高。

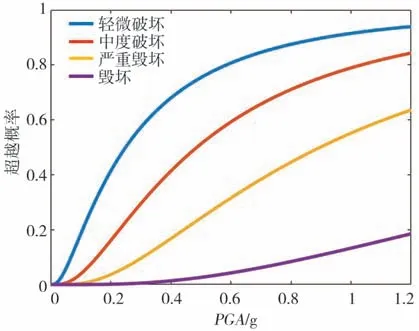
图9 拱桥地震易损性曲线（补充数据）Fig.9 Seismic fragility curve of arch bridge（supplementary data）

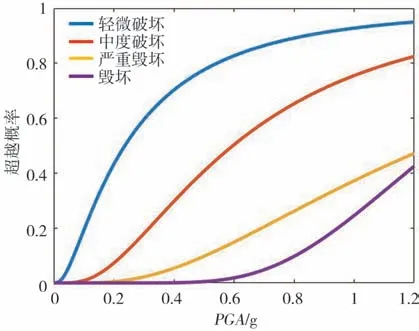
图10 梁桥地震易损性曲线（补充数据）Fig.10 Seismic fragility curve of girder bridge（supplementary data）

表3 易损性函数的参数估计值（补充数据）Table 3 Estimated parameter of fragility function（supplementary data）

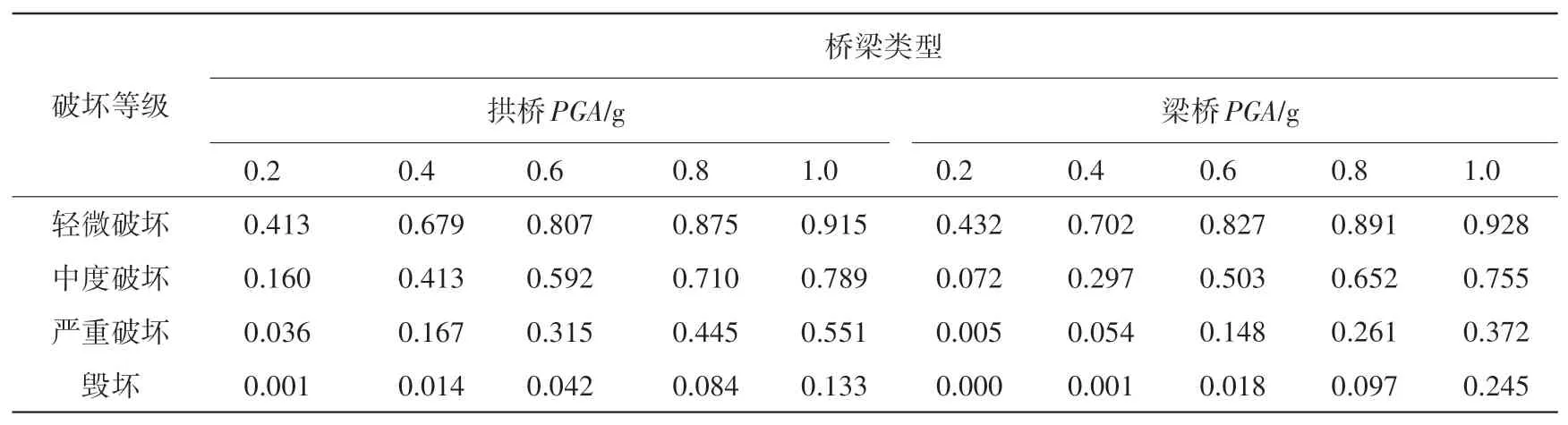
表4 不同类型桥梁的地震破坏超越概率（补充数据）Table 4 Exceedance probability of earthquake damage in different bridge types（supplementary data）

4 基于震害数据的桥梁地震平均损失率模型

概率损失模型表达形式为结构的损失比与概率易损性曲线的乘积，如式（4）所示，损失比是指结构发生不同程度的破坏时，用来修复或重建的费用与原造价的比值，

式中：RM代表平均损失率；Pi代表第i等级的破坏概率；Ri代表第i等级的结构损失比；i取1～5，分别代表结构完好、轻微破坏、中等破坏、严重破坏以及毁坏。

目前，常用的损失比确定方法有：（1）资料统计法；（2）专家咨询法；（3）界限状态估计法；（4）估计震损程度法。文中选用中华人民共和国国家标准《地震现场工作第4部分：灾害直接损失评估》（GB/T18208.4-2011）［10］给出的公路系统工程结构的地震损失比，如表5所示。

表5 公路系统工程结构破坏损失比Table 5 Damage loss ratio of highway system engineering structure %

采用补充数据回归得到的桥梁易损性模型，根据式（4）及表5可得到山区桥梁地震平均损失率模型。通过图11可以发现，随着PGA的增加，拱桥及梁桥的平均损失率逐渐增长，拱桥呈现出先快后慢的趋势，梁桥呈现出先慢后快的趋势。

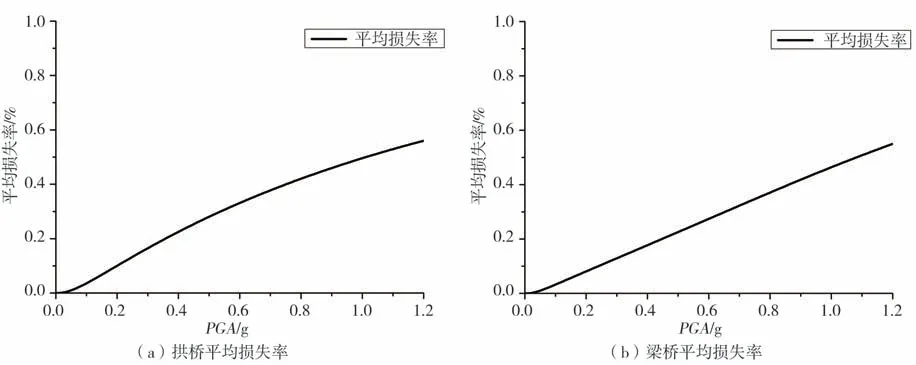
图11 桥梁平均损失率Fig.11 Average loss rate of bridge

在地震发生后可以根据此模型快速地估算出山区桥梁的损失，再结合隧道、公路等结构的震害损失，就可以得到震害地区交通系统总的震害损失。

5 结论

（1）文中根据汶川地震桥梁震害资料，通过回归的方式得到了山区拱桥与梁桥的地震易损性模型。发现当采用调查数据回归得到的易损性曲线，其轻微破坏条件下的超越概率在小于0.1 g时就已经超过了60%，这与实际情况不符，因此按照烈度区面积大小对完好桥梁数据进行补充，得到的桥梁易损性曲线得到了明显改善。

（2）通过对比梁桥与拱桥的地震破坏超越概率，可以发现梁桥在地震作用下发生毁坏的概率更高。

（3）采用补充数据回归得到的桥梁易损性模型，结合桥梁结构发生某一种破坏状态时的损失比，建立了桥梁结构的平均损失率模型，随着PGA的增加，拱桥及梁桥的平均损失率逐渐增长，由于拱桥轻微破坏、中度破坏、严重破坏下的地震易损性的增长逐渐放缓形成了拱桥平均损失率呈现出先快后慢的趋势，而梁桥在毁坏情况下的地震易损性增长速度较快造成了梁桥呈现出先慢后快的趋势，依据本文建立的桥梁地震易损性模型及平均损失率模型可以在将来发生地震时快速地进行地震损失评估。