氢键型水凝胶自修复行为的Monte Carlo模拟

高慧玲，曹珍珍，顾芳，王海军，2，3

（1.河北大学化学与环境科学学院,2.河北省化学生物学重点实验室,3.教育部药物化学与分子诊断重点实验室,保定 071002）

近年来，自修复水凝胶因其超强的自主修复能力和良好的生物相容性而备受关注［1～3］.目前，一些自修复水凝胶已经被用于药物释放［4，5］、伤口敷料［6～9］以及软组织工程等生物材料领域［10～12］，并在3D打印［13，14］及软机器人［15］等实际应用中表现出可观前景.在此类材料中，动态键型自修复水凝胶因能够通过可逆交联实现自修复而成为热点之一［16～25］，其中的动态键主要包括氢键［21～23］、二硫键［24］及酰腙键［25］等键型.研究表明，水凝胶中的多重氢键作用可具有接近类共价键的强度，因而可以提高其力学性能［26］.由此可见，在自修复凝胶中引入多重氢键不仅可以提高其自修复性能，也可使其力学性能得到显著的改善［26～29］.

本文首先根据氢键型凝胶的特征构建了凝胶断面的格气（Lattice gas）模型［30］，进而通过Monte Carlo模拟验证了其自修复行为在本质上属于一级热力学相变，并由比热的峰值确定了凝胶自修复的临界联结分数.在此基础上，研究了氢键强度、合作效应以及平均断面间距等对凝胶自修复行为的影响，旨在揭示它们对氢键型凝胶自修复行为的调控机制.

1 氢键型自修复凝胶的Monte Carlo模拟算法

在氢键型自修复凝胶材料中，构筑单元之间的氢键作用维系着凝胶的稳定性，并表现出动态平衡特征.当将凝胶沿着某一横截面断开后，可将凝胶断面抽象为数目为N的二维格子.显然，2个断面上的联结基团（质子受体和给体）呈现出互补性，因而可以选取其一予以讨论.若以ni，α表示第i个格子中第α个基团的联结状态（ni，α=0和1分别表示断开和联结），则描述氢键型凝胶自修复过程的能量函数可表示为

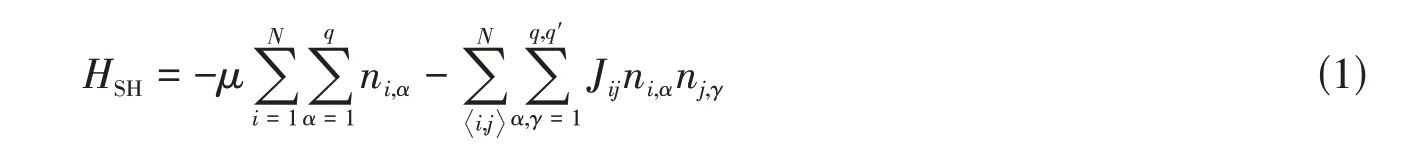
式中：μ表示每个联结单元的联结能（氢键键能）；符号i，j表示对最近邻格子指标求和；Jij为最近邻交联单元之间的相互作用能；而q和q′表示每个格子中质子给体和受体的数目.对于某一格点而言，当其形成氢键后，其最近邻格点上对应单元之间的距离将随之减小，从而在一定程度上增加了近邻格点形成氢键的概率.由此可见，参数Jij本质上表示了格点间合作效应的强弱.式（1）中的能量函数在本质上属于格气模型，既描述了凝胶上下断面之间对应格子形成氢键时的能量变化，又描述了同一断面上不同格子间的协同作用.

假设断面上的每个格子中或含有a个质子受体或含有d个质子给体，当它们接近到一定距离时即可形成氢键，以此实现自修复.进一步引入断面间距的特征尺度b（超过b时凝胶不能实现自修复），则断面对应单元间的联结分数（f）将依赖于平均断面间距lb（l为平均断面间距参数，0≤l≤1）.根据统计力学原理，可以得到描述氢键形成的质量作用定律如下［31，32］：

式中：β=1/（kBT），kB为玻尔兹曼常数，T为体系的绝对温度；λ表示某个格子上下断面间的氢键数；参数ω则与氢键形成过程中的熵变相关［33］.通过计算λ与a或d的比值可以得到格子的联结分数f.显然，某一格点因联结所致的能量变化与氢键强度（βμ）和近邻格点的状态直接相关.值得说明的是，氢键强度参数的影响实际上也喻示着在氢键键能一定时温度的作用.为了简洁起见，本文选择平面四方格子进行研究，并将相互作用能Jij统一取值为J，即Jij=J.

由式（2）可以看出，参数μ，J，l以及温度T等共同调控着氢键型凝胶的自修复行为.本文利用正则系综下的Monte Carlo方法［34］进行模拟，旨在阐明相关因素对氢键型凝胶自修复行为的调控机制，模拟步骤如下：（1）设定初始断面间距，使格点上的交联单元均处于断开状态，进行初始化；（2）尝试改变一个单元的状态，并计算所产生的能量变化ΔE和联结分数f；（3）调取随机数r并判断该单元是否接受改变，由此调整相关物理量；（4）重复步骤（2），直至遍历所有格子，完成一个Monte Carlo步；（5）进行多个循环模拟，直至体系平衡，检查所得联结分数是否达到临界联结分数（fc），由此判定体系是否实现自修复.

2 氢键型凝胶自修复行为的相变本质及影响因素

众所周知，凝胶断面之间的充分接触是实现自修复的必要条件.在合适的断面间距下，联结单元间的氢键强度越大，凝胶的自修复效果越好.同样，联结单元之间的空间关联性（合作效应）也会对凝胶的自修复造成影响.因此，通过Monte Carlo方法对氢键型凝胶的自修复行为进行研究可以揭示相关因素对自修复行为的具体影响.在本文的模拟中，将a和d均固定为2，而参数ω的值则取作100.

2.1 氢键型凝胶自修复行为的比热变化及相变本质

当凝胶断面上对应格点之间形成氢键时，其联结过程通常用比热的变化加以描述.鉴于此，本文将对自修复过程中的比热（CSH）进行模拟，并以此确定临界联结分数.首先在不同的氢键强度（βμ）以及不同的合作效应（μ/J）时进行模拟，图1给出了CSH和f在不同μ/J下随着βμ的变化情况.

图1表明，在氢键型凝胶自修复的过程中，不同合作效应下的比热变化曲线均存在明显的峰值.实际上，由于式（1）中的能量函数与Ising模型等价［30］，因而在统计力学中基于Ising模型所得出的相关结论同样有效.这意味着此类凝胶的自修复行为在本质上属于一阶热力学相变，而模拟结果也确认了这一结论.结果同时表明，只有当联结分数高于比热峰值所对应的临界值（fc）时，凝胶材料才能实现自修复，从而使其达到稳定状态.由图1可以看出，虽然比热变化曲线峰值不同，但峰值处的氢键强度所对应的fc几乎保持不变.因此，本文选取fc=0.68为凝胶能否实现自修复的判据.

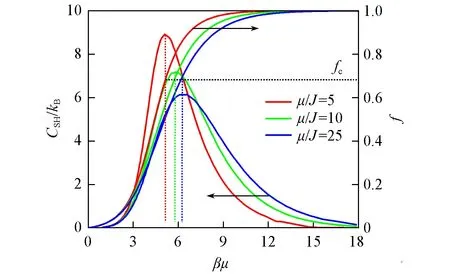
Fig.1 Specific heat(CSH)and association fraction(f)against βμ under different μ/J

2.2 氢键强度对凝胶自修复行为的影响

在氢键型凝胶的自修复过程中，上下断面的对应单元间形成氢键后将导致能量降低，且氢键强度越大，能量的降低也越多.因此，氢键强度的大小将直接影响凝胶的稳定性.为了阐明βμ对f的具体影响，分别在l=0.5时及μ/J=8时改变相关参数进行模拟，结果如图2所示.图2（A）为当设定初始断面间距参数l时，不同合作效应下f随βμ的变化趋势；图2（B）为当μ/J固定时，f在不同参数l下随βμ的变化趋势.

Fig.2 Plots of f against βμ under various conditions（A）l=0.5 at different μ/J；（B）μ/J=8 at different l.

由图2可以看出，联结分数均随着氢键强度的增大而增加.显然，当氢键强度相同时，合作效应越大（对应μ/J的数值越小），联结分数越高.由图2（B）可知，当μ/J固定时，l越小，则体系到达同一联结分数所需的氢键强度也越小.表明凝胶断面接触越紧密，凝胶的自修复效率越高.值得指出的是，当βμ很小时，即使合作效应很大或平均断面间距很小，仍然无法达到临界联结值fc，即凝胶不能实现自修复.由此可见，氢键强度是凝胶自修复过程的关键因素，而选择联结能较大的交联单元将有助于氢键型凝胶实现自修复.

2.3 合作效应对凝胶自修复行为的影响

在凝胶断面上，某一单元与其相邻单元的协同作用表现为合作效应.为了考察合作效应对氢键型凝胶自修复行为的影响，分别在βμ=5.0和l=0.5时进行模拟，相应的f随着μ/J的变化的趋势如图3所示.

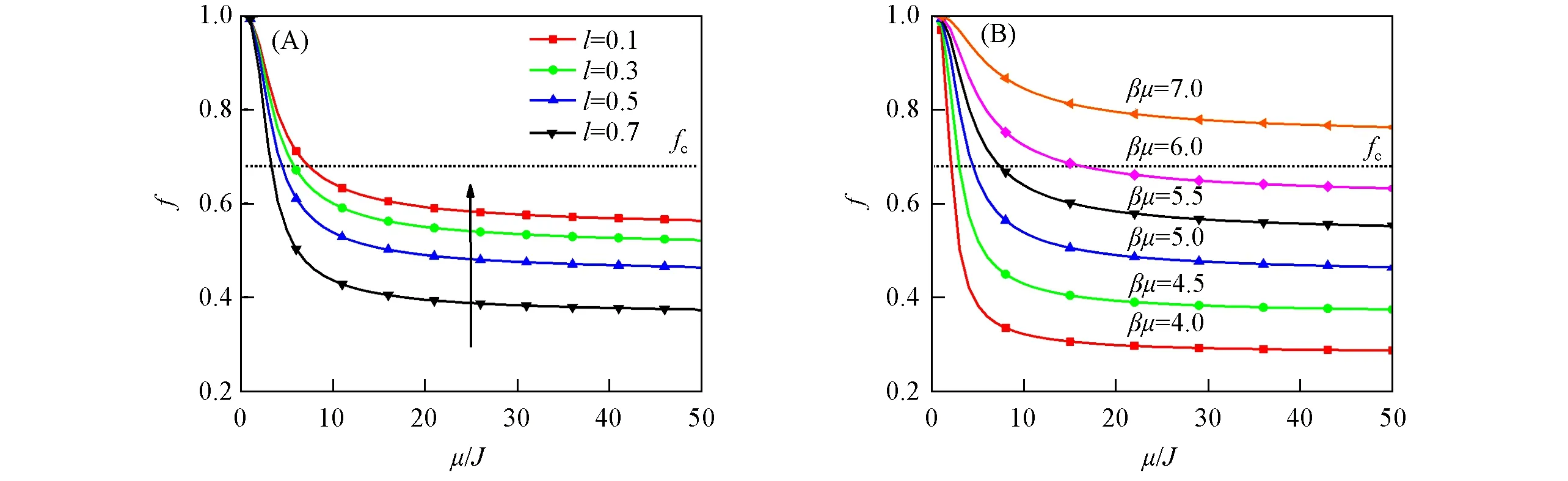
Fig.3 Plots of f against μ/J under various conditions（A）βμ=5.0 at different l；（B）l=0.5 at different βμ.

由图3（A）可知，联结分数随着合作效应的逐渐增强（对应μ/J的数值减小）而逐渐增加.在μ/J相同的条件下，平均断面间距l越小，联结分数越高.而当合作效应较弱时，f甚至无法到达临界联结分数fc，从而表明凝胶实现自修复需要一定程度的协同作用.在图3（B）中，合作效应随着μ/J的不断增加而不断减弱.进一步对比不同氢键强度下的曲线可知，氢键强度越小，联结分数降低得越快.当μ/J一定时，氢键强度越小，体系到达临界联结分数所需的合作效应越大.同时，当μ/J的数值较大时，联结分数的变化曲线逐渐趋于平稳，表明较弱的合作效应对凝胶的自修复过程影响甚微.

2.4 断面间距对凝胶自修复行为的影响

在凝胶的自修复过程中，断面间距的逐步减小代表着凝胶材料自修复的动态过程，这与实际情况相对应.如前所述，当断面间距超过特征尺度b时，凝胶材料将无法实现自修复.因此，平均断面间距参数l也是凝胶自修复的影响因素之一.为分析l对凝胶自修复行为的影响，图4（A）给出了在βμ=5.0及不同μ/J下f随l的变化趋势，图4（B）则给出了在μ/J=8及不同βμ下f随l的变化趋势.

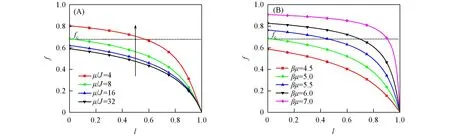
Fig.4 Plots of f against l under various conditions（A）βμ=5.0 at different μ/J；（B）μ/J=8 at different βμ.

由图4可以看出，联结分数随着平均断面间距的增大而逐渐降低.若l较小时f仍然低于fc，表明材料不能达到凝胶的稳定状态.图4（A）结果表明，当l相同时，合作效应越显著，则联结分数也越大；而当合作效应较弱时，凝胶体系的联结分数甚至无法达到临界联结分数.由图4（B）可知，氢键强度越大，体系到达同一联结分数所需的断面间距越小；当氢键强度过低时，体系同样无法到达fc.由此可见，只要合作效应和氢键强度适当，即使在断面间距较大时，联结分数依旧可以达到和超过fc，从而有助于凝胶实现自修复.

3 氢键型凝胶自修复过程的动态特征

在以上模拟平均断面间距对凝胶自修复行为的影响时，均设定了一个初始断面间距参数l，并通过不断减小其初值来表征凝胶的自修复过程.事实上，当某一格点形成氢键时，其近邻格点上对应单元之间的距离亦将相应减小.这意味着形成氢键的格点会导致相邻格点的断面间距有所减小，从而促进氢键的形成.因此，研究氢键型凝胶自修复行为的动态特征、揭示自修复时间的影响因素等可为相应的功能材料的设计和开发提供理论线索.

假设当某一个格点形成氢键时，其近邻未成键格点对应单元间减小的距离为cb.因此，若同时记录联结分数到达临界联结分数时的时间（Monte Carlo Step，MCS），即可阐明相关因素对自修复时间的影响.图5（A）给出了当c=0.001且μ/J=8时，在不同初始断面间距下，自修复时间随氢键强度的变化情况；图5（B）则给出了在c=0.001且l=0.99时，不同合作效应下自修复时间随氢键强度的变化.

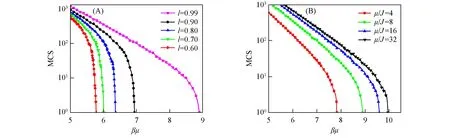
Fig.5 Plots of MCS against βμ under various conditions（A）μ/J=8 at different l；（B）l=0.99 at different μ/J.

图5结果表明，氢键强度越大，凝胶体系的联结分数到达临界联结分数所需的时间越短，即氢键强度越大，凝胶实现自修复就越迅速.由图5（A）可以看出，自修复时间在不同初始断面间距下也有所不同.当氢键强度一定时，自修复时间随着l的减小逐渐减小，这意味着合适的初始断面间距可以加快凝胶的自修复过程.图5（B）结果表明，在同一氢键强度下，合作效应越大（对应的μ/J数值越小），自修复时间越短.当合作效应和氢键强度足够大时，自修复时间也非常短.因此，在自修复凝胶体系中，凝胶网络应当尽可能致密以提高单元间的合作效应，从而有效缩短凝胶材料自修复的时间.需要指出的是，凝胶断面的形貌起伏和弹性等也可影响其自修复行为［35～38］，这有待进一步深入研究.

4 结论

通过Monte Carlo模拟方法研究了氢键型凝胶材料的自修复行为.首先基于格气模型和Ising模型的等价性，指出氢键型凝胶的自修复行为属于热力学一阶相变，以此获得凝胶自修复的临界联结分数作为其实现自修复的判据.在此基础上，考察了氢键强度、合作效应和断面间距对自修复行为的具体影响.结果表明，氢键强度是影响凝胶自修复的关键性因素.同时，初始断面间距和联结单元间的合作效应对凝胶自修复有着明显影响.模拟结果可为设计合成具有一定结构和功能的氢键型自修复凝胶材料提供理论参考.