不等直径并排塔器风致振动特性分析

郭 凯，程雨轩，蒋建旭，樊显涛，张红升

(1.燕山大学 河北省水体重金属深度修复与资源利用重点实验室，河北秦皇岛 066004；2.燕山大学 环境与化学工程学院，河北秦皇岛 066004；3.天津大学 化工学院，天津 300000)

0 引言

塔器是化工和石油生产中的重要设备，其投资占整个工艺设备总投资的25%～45%[1]。随着石化行业精细化和高效化发展，单座塔器已经无法满足生产的需求，因此出现了不等直径并排塔器这种新型组合的化工设备，这些塔器呈现直径不同、并列密排的特点，且各塔之间相互独立。塔设备作为一种露天直立设备，不可避免地承受风载荷，极易发生风致振动，造成塔器破坏失效，因此在设计中必须考虑风致振动的问题。但由于此类设备周围的流场涉及剪切层、间隙涡和尾流之间的复杂耦合作用，国内塔器设计标准已不适用于这种特殊结构塔器的设计，导致并排塔器的风致振动设计无据可依。因此对此类塔器的风致振动特性进行研究十分必要，可以为并排塔器的设计提供一定的理论基础。

塔器风致振动问题，本质上是圆柱绕流的气动力学问题，当流体流经圆柱表面时，会在其两侧交替产生漩涡脱落，引起其在横流向发生周期性振动。单座塔器的风致振动主要是由卡曼涡街引起的单圆柱涡激振动，目前国内许多学者[2-5]对单塔的风致振动响应进行了研究，已经形成了较为完整的理论体系和设计准则。对于并排塔器所构成的多圆柱绕流问题也一直受到国内外学者的广泛关注。滕丽娟[6]对雷诺数Re=200的多圆柱绕流的流场特性和气动力系数进行了系统研究，表明间距比对流场特性有很大的影响。SUMNER[7]对双圆柱绕流的流场特性和尾流特征进行了详细地总结。谭蔚等[8]对三座并排塔器的流场特性进行了数值研究，表明在小间距比的塔器之间存在强耦合区。及宁春等[9]对雷诺数Re=100条件下串列双圆柱的流致振动进行了研究，结果表明，间距比的变化改变了双圆柱的振动响应和尾流脱落特性。ASSI等[10]在水洞中对串列双圆柱流致振动响应进行了试验研究，结果表明上游圆柱产生的旋涡可以促进下游圆柱的振动，使其振幅变大；同时，将这种振动现象命名为尾流驰振。樊显涛等[11]对串联、并排和交错布置的并排塔器流致振动的振动特性和尾流影响区进行了试验研究，结果表明间距比和攻角对并排塔器的振动响应都有明显的影响。

综上所述，虽然已有一些学者对多圆柱流致振动和并排塔器风致振动问题进行了研究，但是不等直径并排塔器风致振动的研究还比较匮乏。美国ASME-STS—2016SteelStacks和谭蔚等[12]研究结果都表明，对于并排塔器，当塔器的间距比较大时，无需考虑塔器之间耦合作用，可视为单座塔器设计计算；当间距比较小时，塔器之间的耦合作用将会变得非常复杂，塔器振动响应也会变得复杂。又由于塔器通常处于亚临界雷诺数的工作环境，且在风载荷作用下的横风向振动最为剧烈，振幅可达到顺风向的8～10倍[11]，更易发生破坏。本文通过大涡模拟，在直径比d/D=0.4～1.0范围内，对亚临界雷诺数和小间距比(L/D=1.5)条件下的不等直径并排塔器的风致振动响应进行数值研究，旨在为不等直径并排塔器的设计计算和振动分析提供理论依据和参考。

1 数值方法和计算模型

1.1 控制方程

本文采用基于滤波N-S方程和刚体方程的流固耦合算法来研究圆柱体的振动响应。由于雷诺数处于亚临界区，可能导致流动不稳定，存在旋涡脱落的情况，流场以大尺度涡为主导，又伴随大量小尺度涡结构，为了能更好地模拟流场中的湍流旋涡，捕捉到更完善的流场脉动信息，故采用大涡模型(LES)作为流体模型来求解滤波N-S方程。流体运动控制方程[13]为:

(1)

(2)

(3)

式中,δij为克罗内克函数；vsgs为解决Smagorinsky亚格子尺度模型的粘度表达式，见式(4)[14-15]。

(4)

式中,Δ为有限元的网格尺寸;Cs为Smagorinsky常数，本文取0.18;S为应变率。

对于实体模型，圆柱体被视为刚体，模型简化为单自由度质量-弹簧-阻尼系统，如图1所示。其运动由受迫阻尼振动方程控制：

图1 简化圆柱体运动模型示意

(5)

式中,y″,y′,y分别为圆柱体横流向振动的加速度、速度、位移，圆柱均从静止开始振动；Ur为折合速度,Ur=U∞/(fnD)；fn为圆柱体的固有频率；m*为质量比，m*=4m/ρπD2l；m为圆柱体质量；l为圆柱体长度；ζ为阻尼比；f为式(1)计算出的流体力。

1.2 计算模型

为减少壁面和尾流区域对圆柱振动的影响，流场计算区域取为20D(30D+L)的矩形区域[14]，上游圆柱中心距离入口边界为10D，下游圆柱中心距离出口边界为20D，圆柱中心距离上下边界各为10D，如图2所示。流场计算域采用以六面体为主的非结构网格进行网格划分，其中圆柱附近及尾流区域进行网格加密处理，图3(a)示出全局网格。为获取圆柱表面的旋涡脱落信息，设置10层膨胀边界层网格，LES模型需要对边界层网格进行严格的控制以确保y+≤1，故边界层第一层网格高度设置为0.005D，如图3(b)所示。

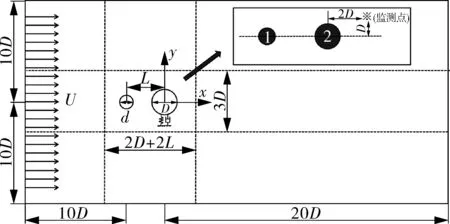
图2 流场计算区域示意

图3 计算网格示意

本文采用Ansys CFX求解器进行求解，湍流模型选择LES模型，瞬态方案选择二阶反向欧拉方案，对流项求解格式为中心差分格式。入口边界设定为均匀流速，出口边界设定为压力出口，上下壁面和圆柱体壁面设定为无滑移边界条件。实际钢制塔器属于小质量阻尼体系，NB/T 47041—2014《塔式容器》推荐塔器的质量阻尼比小于10，本文选取的圆柱体动力学参数如表1所示，尽管与实际塔器的参数不是完全相同，但都属于小质量阻尼体系，雷诺数处在亚临界区，则圆柱的振动特性基本相似，研究结果具有普适性。为了消除因网格质量对计算结果可能带来的影响，并在合理时间内使计算收敛并得到满足精度要求的数值解，本文以直径比d/D为0.8、折合速度为10条件下，采用3种疏密不同网格计算比较下游圆柱横流向振幅值y，网格无关性验证结果见表2，网格尺寸设置为0.0375D足以得到合理的结果。

表1 串联圆柱体参数

表2 网格无关性验证(d/D=0.8,Ur=10)

为了验证上述模拟方法、模型、网格和边界条件的准确性，本文开展了与文献中单圆柱涡激振动[16]和串列双圆柱流致振动[17]试验数据对比，如图4所示。图4(a)示出不同折合速度下单圆柱涡激振动横流向振幅，可以看出，模拟结果与试验结果较为吻合，可以较好模拟单圆柱典型的涡激振动响应。此外，图4(b)对比了两个串联圆柱的振动响应，可以发现，本文的模拟结果与试验数据依旧一致。通过与试验数据对比，证实了本文数值模拟的准确性。

(a) 单圆柱横流向振幅

2 结果与讨论

2.1 振幅响应

由于一定条件下圆柱振动具有不规律性，为了合理衡量圆柱振动大小，直观了解圆柱振动响应，将振动无量纲振幅比定义为:

A/D=Yrms/D

(6)

式中,D为下游圆柱直径，m；Yrms为下游圆柱横向振动位移的均方根值，m。

图5示出在不同直径比时，下游圆柱振幅响应A/D随折合速度Ur的变化曲线。可以看出，单圆柱振幅响应只有一个峰，圆柱只呈现涡激振动响应，而双圆柱振动响应曲线均出现了两个峰值，分别对应着涡激振动与尾流驰振两种响应。这与KHAN[18]等的结果相一致，但是与GUSTAVO等[10]的小雷诺数下的试验结果存在较大不同，这表明雷诺数对串列圆柱的流致振动有较大的影响。

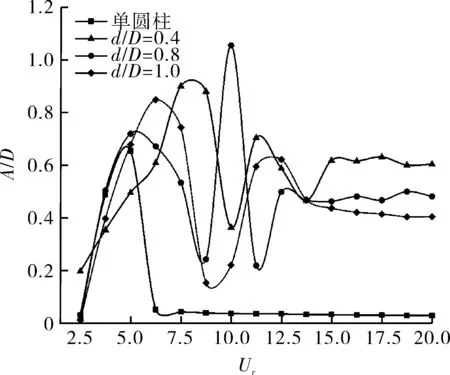
图5 不同直径比时，A/D随Ur的变化曲线

对于不等直径双圆柱，下游圆柱的最大振幅比单圆柱和等直径双圆柱的情况都要大，当d/D=0.8时，最大振幅比单圆柱要大近40%，且随着d/D增大，最大振幅响应对应的折合速度也越大。在Ur>7.5的高折合速度范围内，与单圆柱振动响应相比，双圆柱的振幅会依旧维持较大的值。由此可见，相较于单座塔器，并排塔器振动会变得十分剧烈，特别是不等直径并排塔器在实际工况中会比较危险。

为进一步分析圆柱的振动机理，图6示出在d/D=0.8,Ur=2.5，10工况下，圆柱在一个振动周期内指定时刻的压力云图、瞬时涡量和流线图。可以看出，当Ur=2.5时，上游圆柱形成的涡结构不能在圆柱间隙中释放，而是重新附着在下游的圆柱上并在其顶部和底部脱落，在尾流中产生一个2S模式涡街[19]，同时，在圆柱间隙之间形成两个对称的再循环区，并下游圆柱处形成一个几乎对称的低压区。这种尾流脱落模式和压力的平衡分布导致圆柱的轻微振动。当Ur=10时，从上游圆柱体脱落的涡结构在间隙区域释放，然后冲击下游的圆柱，使低压区和涡冲击点沿下游圆柱周期性偏移，导致圆柱剧烈振动。此时，尾流发展为P+S 模式，可以观察到一个旋涡对和一个单旋涡在下游尾流的相反两侧脱落。

(a)指定时刻

2.2 频域响应

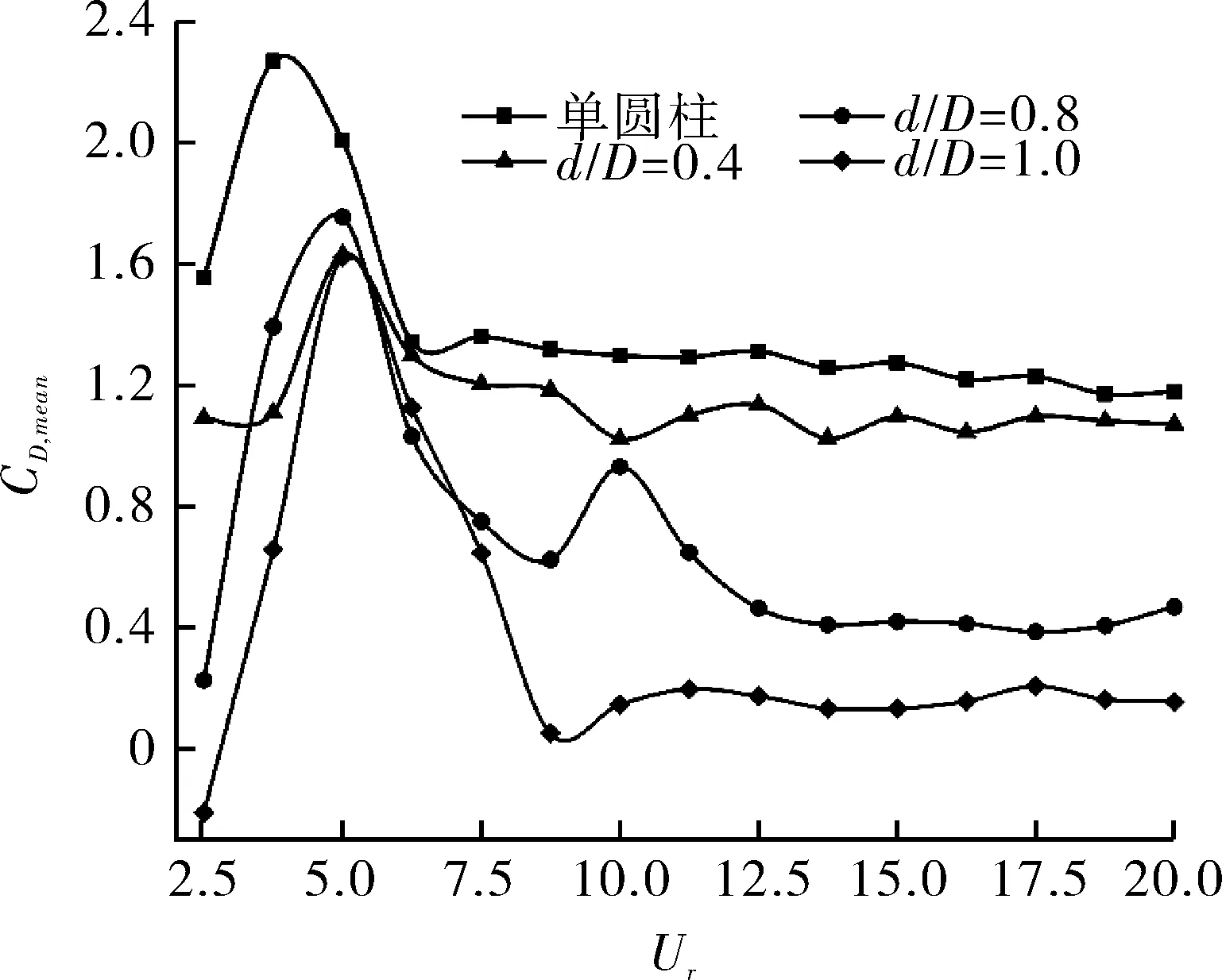
对于圆柱结构的流致振动问题，当圆柱的振动频率与固有频率接近时(即f/fn趋近于1.0，文中以0.9≤f/fn≤1.1为界)，一般认为圆柱响应发生了振动锁定现象，通常圆柱振动频率f取振动功率谱中的主频。图7示出不同直径比时，下游圆柱振动频率比f/fn随折合速度Ur的变化关系。可以看出，单圆柱只存在一个锁定区为3.75

图7 不同直径比下，振动频率比f/fn随折合速度Ur的变化

图8示出不等直径比时，部分折合速度(Ur=3.75，5，7.5，10，17.5)的下游圆柱振动位移PSD曲线的变化情况。可以看出不同情况下的圆柱振动频率主频及次频的数量、位置以及所对应的能量大小，可进一步理解圆柱振动响应的变化规律。在振动位移PSD图中，振动频率的阶数越高，圆柱振动响应就会越复杂，主频所对应的能量越高，圆柱的振幅就越大。由图8可知，在小折合速度(Ur=3.75，5)内双圆柱振动PSD曲线中仅有一个主频且都在固有频率附近，对应的能量较大，也没有出现复杂的次频，随着Ur的增大，主频及所对应的能量值随折合速度变化变得更加复杂，在主频的周围和大约3倍主频处出现多个次频，使得圆柱的振动响应呈现为多种模式共同作用的情况。与图5的振幅响应相一致，在锁定区内主频接近固有频率，此时圆柱振动较剧烈。另外，在大折合速度(Ur=17.5)时，双圆柱振动PSD曲线出现更加复杂的多频现象，会影响能量在流体与圆柱之间的传递，从而改变圆柱的动力响应。

图8 不同直径比下，下游圆柱振动位移PSD变化情况

2.3 受力特性

2.3.1 升力特性

升力系数是一个无量纲数，其表达式为:

(7)

式中,CL为圆柱升力系数;FL为圆柱所受的升力，N;ρ为空气密度，kg/m3;U∞为自由来流速度，m/s;l为圆柱长度，m。

在不同直径比下，圆柱升力系数均方根值CL,rms随折合速度Ur的变化曲线如图9所示。对于单圆柱，在低折合速度下CL,rms随Ur的增大而减小，在Ur=4.25附近达到极小值0.18，之后在锁定区内，CL,rms随Ur的增大而缓慢增大，在锁定区的上限Ur=6.25处达到峰值0.9。而在高折合速度(Ur≥7)下，CL,rms几乎不再随Ur的增大而发生变化。对于双圆柱的情况，当d/D=0.4时，CL,rms随Ur的变化趋势与单圆柱类似，在低折合速度下CL,rms随Ur的增大而减小，在Ur=5附近达到极小值0.21，然后CL,rms随Ur迅速增大，之后随Ur的增大缓慢降低，并趋于稳定。对于d/D=0.8和1.0的情况，随着Ur的增大，CL,rms均呈现不稳定的多峰趋势。在低折合速度下，CL,rms随Ur的增大而增大，在Ur=4.25附近到达第1峰值，这一变化趋势与d/D=0.4情况完全不同。随后CL,rms开始减小、然后再增大，在Ur=7.5到达第2峰值。当进入高折合流速后，CL,rms开始趋于稳点不再随Ur的增大而变化。在较高折合速度内，下游圆柱的CL,rms都小于单圆柱的情况，并且较大的直径比对应较小的升力系数。

图9 不同直径比下，CL,rms随Ur的变化曲线

2.3.2 阻力特性

与升力系数相似，阻力系数也是一个无量纲数，其表达式为:

(8)

式中,CD为圆柱阻力系数;FD为圆柱所受阻力，N。

图10示出在不同直径比下，圆柱平均阻力系数CD,mean随折合速度Ur的变化曲线。总体上，单圆柱CD,mean在各折合速度下均要大于双圆柱的结果。对于不等直径双圆柱的情况，圆柱阻力系数平均值CD,mean随折合速度的变化趋势与图5中的振幅曲线基本一致，均出现多个峰值，且取得峰值对应的折合速度也相当接近。在较大折合速度(Ur>10)下，随着直径比的增大，由于上游圆柱的屏蔽作用增强，下游圆柱CD,mean减小。

图10 不同直径比下，CD,mean随Ur的变化曲线

3 结论

(1)不同于单座塔器，并排塔器不仅会出现涡激振动响应，还会出现驰振响应，且下游塔器的振幅明显大于单座塔器(A/D=0.61)，最大振幅比单圆柱的情况增大近40%～45%。对于不等直径比并排塔器，随着折合速度的增大，下游塔器的振幅响应呈现多峰状态。随着直径比的增大，上游塔器的遮蔽作用增强，下游塔器的振幅比变化较大，对锁定区的峰值与宽度都有一定影响。

(2)与振幅响应相一致，单座塔器只存在一个锁定区，而并排塔器呈现涡激振动和尾流驰振两种响应，其锁定区范围较单圆柱大；并且不等直径并排塔器锁定区范围和开始锁定的折合速度在不同的直径比时，也呈现不同的状态。

(3)对于并排塔器，不同直径比下升力系数的均方根值呈现出不同的变化趋势，且较大的直径比对应较小的升力系数；不同直径比的塔器阻力系数平均值随折合速度的变化趋势接近于塔器的振幅曲线，并且单座塔器的阻尼系数均大于并排塔器。