大型弓形截面螺旋管中流体流动与传热性能研究
2022-11-15李维聪李慧芳吴志伟钱才富
李维聪,李慧芳,尹 霞,吴志伟,钱才富
(1.北京化工大学 机电工程学院,北京 100029;2.河南金心智能科技有限公司,河南新乡 453011)
0 引言
夹套容器广泛应用于石油、化工、医药以及食品加工等领域,通过夹套内的介质来加热或冷却容器内的物料是工业生产中普遍采用的操作方法。作为夹套容器的一种,半管式夹套因具有节省材料、传热效率高、承载能力强以及使用经济等优点,在工业生产中的应用越来越广泛[1-5]。
半管式夹套按其截面形状不同,分为半圆管和弓形管,国内外学者对其流动与传热进行了研究,其中多数研究集中在半圆管夹套上。DHOTRE等[6-7]对半圆管夹套内流体传热进行了试验并给出了传热关联式。李雅侠等[8]通过数值模拟研究了螺旋半圆管夹套的湍流流动与传热,给出了流场与温度场分布,发现增大曲率可增强夹套换热。JAYAKUMAR等[9-10]研究了螺距、螺旋半径以及管径对螺旋盘管流动和传热的影响,并给出了努塞尔数关联式。张静等[11]考察了螺距和搭接结构对半管夹套强化传热的影响。李雅侠等[12]对比了截面圆心角为120°的弓形截面夹套与半圆形截面夹套在相同换热面积下的流动与换热特性,考察了雷诺数与无量纲曲率的影响。WANG等[13]通过PEC和JF评价因子分析了一定雷诺数时的5种不同圆心角弓形截面夹套的综合性能。
目前工程上螺旋半管夹套的制造主要是采用金属板带做原料,金属板带在前后直排的数组成型辊轮中通过,随着辊轮的回转,在将带料向前送进的同时,顺次进行横向弯曲成半圆型,最后进行纵向弯曲成环状[14],如图1所示。这种方法的优点较多:(1)节约材料;(2)可满足长尺寸半圆管的要求;(3)可在容器上直接绕制;(4)比利用管材煨制成型的成本低。所以,从制造的角度看,夹套截面不必非是圆形或半圆形,而且弓形截面夹套相对更容易制造。

图1 螺旋半管夹套的制造现场
本文针对螺旋直径为1 000~4 500 mm的大型弓形截面螺旋管中流体流动与传热性能进行研究,考察在相同流量下,弓形截面形状或圆心角对努塞尔数Nu、摩擦阻力系数f及综合性能评价因子PEC的影响,提出计算弓形截面螺旋管Nu和f的关联式,为弓形截面螺旋管夹套的工程应用提供理论基础。
1 数值模拟模型及验证
1.1 几何模型
本文建立了3圈不同截面圆心角的螺旋弓形半管夹套有限元模型,研究其流动和传热特性。螺旋夹套及其截面形状几何模型如图2所示。为对比传热性能,对于所有不同截面,夹套内筒体侧传热面积相同,因此,不同的截面圆心角对应的夹套截面直径也会不同。本文设定筒体传热面宽度均为80 mm,但应该指出的是,本文在下一节得到的Nu,f与流动状态相关,与筒体传热面宽度没有关系。

图2 螺旋管几何模型示意
1.2 设计参数与边界条件
以常温常压下的液态水为介质,具体的物性参数列于表1,并假定在本研究中保持不变,在温度没有显著变化时,此假设是可以接受的。

表1 水的物性参数
应用CFD Fluent分析软件,选用RNGk-ε湍流模型[15-16],压力和速度耦合采用SIMPLEC算法,除压力项外,其余变量均采用二级迎风格式处理,采用速度入口和压力出口,入口温度设置为20 ℃。壁面边界条件为外侧弯曲壁面无滑移、绝热,内侧直壁面无滑移、恒壁温(80 ℃)。收敛准则为能量残差收敛标准取10-6,其余参数为10-5。
对不同圆心角的弓形截面螺旋管,考察5种体积流量下的流动与传热情况。体积流量qv分别取0.000 65,0.000 80,0.000 95,0.001 10,0.001 25 m3/s,对应的入口速度条件如表2所示。在所研究的体积流量与换热面积下,雷诺数均在10 000~30 000之间,处于湍流状态。设置夹套的目的是对筒体(如反应釜或发酵罐)的介质进行加热或冷却,而在换热量给定的情况下,工程上需计算的是夹套内的流体流量,当然前提是使夹套内流体流动处于湍流状态,以保证传热效率。另外,工程上往往还根据筒体介质温度的变化来调节夹套内的流体流量。所以本文考察弓形截面形状对传热影响是基于流量不变,而不是流速(或雷诺数Re)不变。
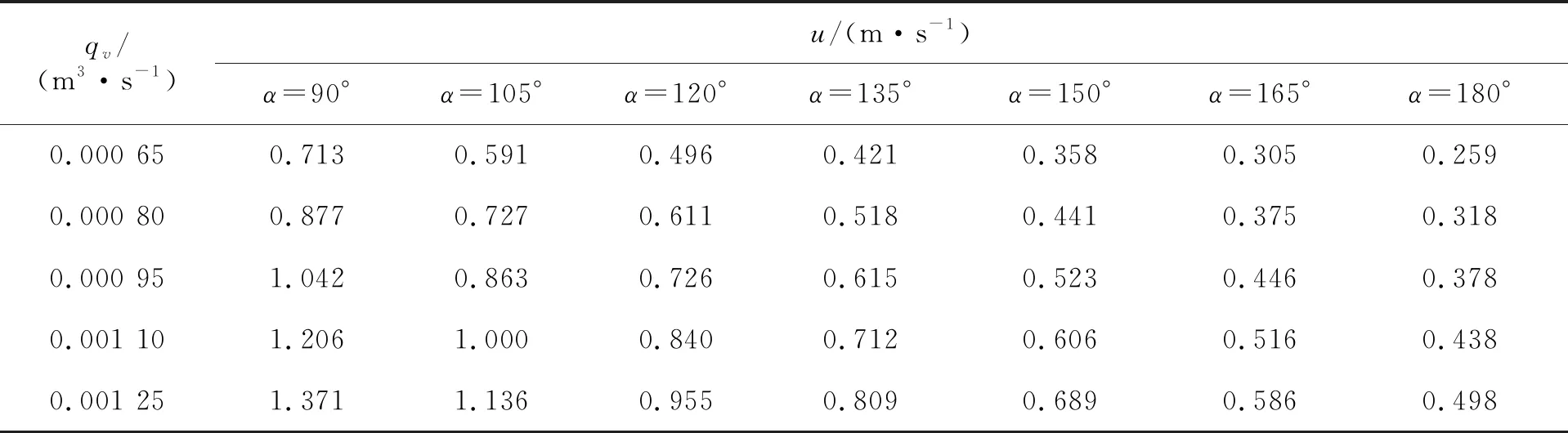
表2 入口条件
1.3 网格划分及模拟验证
网格采用Poly-Hexcore网格进行划分,可以有效减少网格数量,提高求解速度,网格模型如图3所示。网格最小正交质量均大于0.3,质量较好。以Nu和f作为指标进行网格无关性验证,结果列于表3,认为网格数为3 038 612时,可满足网格无关性要求。

图3 螺旋管网格模型示意
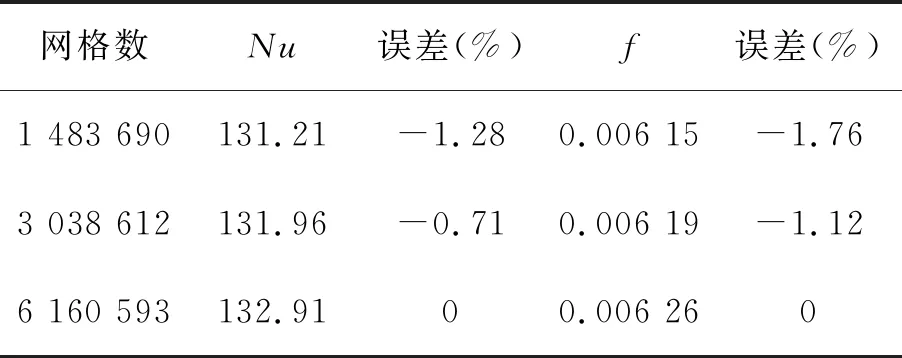
表3 网格无关性验证
在流体流动和传热领域,常用雷诺数Re、努塞尔数Nu、摩擦阻力系数f以及综合性能评价因子PEC反映流动和传热特性,这些参数定义[12,17]如下:
(1)
式中,de为管子当量直径,m,de=4A/p;A为流通截面积,m2;p为润湿周边,m。
(2)
式中,h为换热系数,W/(m2·K);λ为流体导热系数,W/(m·K)。
(3)
式中,ΔP为进出口压差,Pa;ρ为流体密度,kg/m3;L为管子长度,m;u为流体流速,m/s。
(4)
式中,Nu0为α为180°时管内流体努塞尔数;f0为α=180°时管内流体摩擦阻力系数。
为验证数值模拟的准确性,采用上述计算模型,以水为介质,分别计算了3圈圆形截面螺旋管(管径80 mm,螺旋直径2 000 mm)内流体平均努塞尔数Nu和摩擦阻力系数f,计算结果与文献[18-19]给出的关联式进行比较,如下式:
Nu=0.023Re0.85Pr0.4δ0.1
(5)
f=0.076Re-0.25+0.00725(Dc/d)-0.5
(6)
适用范围:Re≥15 000,5≤Dc/d≤2 000。
式中,δ为曲率比,δ=d/Dc;d为管子内直径,m;Dc为螺旋直径,m,Dc=2Rc。
比较结果如图4所示。可以看出,数值模拟与关联式计算结果吻合较好,Nu和f的相对偏差绝对值为3.39%~7.09%和2.18%~6.85%,表明本文计算模型与计算方法是可靠的。

图4 数值模拟结果与经验公式结果对比
螺旋管夹套圈数一般都不止3圈,但本文比较不同截面螺旋管内流体流动与传热性能,3圈是可以反映问题的本质和得出需要的结果;另外,在模拟时进出口都留出一定长度的直管,作用是消除进出口段对数值模拟时管内流动和传热效果的影响,即考虑了进出口效应;还有,研究发现螺距大小对结果影响很小,所以在研究截面圆心角对夹套流动与传热性能的影响时,螺距是固定的,均为240 mm。
2 弓形截面螺旋管流体流动与传热性能模拟
2.1 截面圆心角对流动与传热性能的影响
不同体积流量qv下,Nu与弓形截面圆心角α的关系曲线如图5所示。在图中的5种流量下,不同截面形状螺旋管中流动均在湍流范围,这是工程上螺旋管夹套设计的基本要求。从图中可以看出,不同圆心角的弓形截面螺旋管中Nu随着体积流量的增大而增大,这是因为流量越大,管内流体流速越高;在相同流量下,当α在90°~120°内变化时,Nu几乎不变,当α由120°向180°逐渐增加时,Nu逐渐减小,所以和半圆管相比,弓形管具有传热强化作用。这是因为较小的α对应横截面较小,流速较大。

图5 不同体积流量下Nu随α变化的关系曲线
图6,7示出压力降ΔP/L和摩擦系数f随α的变化曲线,可以看出,单位长度压力降随着α的增加呈递减趋势,f随α的增大而增大。这是因为对于相同的管截面,流量越大,流动损失越大;而对于同样的流量,管子截面越小,流速越大,压力降也就越大。

图6 不同体积流量下ΔP/L随α变化的关系曲线
图8示出了PEC随α的变化曲线。以α为180°的管子为基础,可以看出,当α小于180°时的PEC均大于1,说明弓形截面管子的综合换热性能好于半圆形截面。且随着α的增大,PEC呈单调递减趋势,说明α越小,管子综合性能越好。当α在90°~180°范围内,α=90°时夹套的综合传热效果最好。

图7 不同体积流量下f随α变化的关系曲线

图8 不同体积流量下PEC随α变化的关系曲线
对于给定的板带,其厚度是一定的,因此弓形管耗材可由管子长度与润湿周边的圆弧长度的乘积(即曲边面积)来反映。图9示出了5种体积流量下,α在90°~180°范围内传递相同热量所消耗的材料大小(以曲边面积表示)。可以明显看出,流量越大,弓形管耗材越少。这是因为α角度一定时,流量越大,流速越大,Nu越大。而对于给定的换热量,流量越大,意味着进出口温差越小,加上Nu提高,因此,所需要的管子长度越短,所消耗的材料也就越小。由图9还可看出,截面圆心角越小,弓形管耗材越少。因为相同的体积流量下,α越小,弓形管传热性能越好,所以较小的换热面积即可传递相同的热量。在本研究范围内,α=90°的弓形管子耗材最少,比半圆形截面管减少约71.6%。

图9 弓形管耗材随α变化的关系曲线
2.2 弓形截面螺旋管流体流动与传热准数Nu与f关联式拟合
鉴于关联式(5)(6)适用于计算圆形截面螺旋管流体流动与传热准数Nu和f,本节针对横截面为弓形的螺旋管,考虑参数α对Nu和f的影响,提出弓形截面螺旋管流体流动与传热准数Nu,f关联式。
基于关联式(5)建立的弓形截面螺旋管Nu关联式形式如下:
(7)
基于关联式(6)建立的弓形截面螺旋管f关联式形式如下:
(8)
式中,C,M,N,a,b,c为待求系数。
对表4中的不同结构参数组合的弓形螺旋管进行数值模拟,得到10 000≤Re≤30 000范围内的Nu和f,应用IBM SPSS Statistics软件非线性回归进行拟合,得到系数C,M,N,a,b,c。

表4 弓形截面螺旋管结构参数
修正后的关联式为式(9)和式(10),其适用范围为:10 000≤Re≤30 000,90°≤α≤180°,40 mm≤d≤106 mm,1 000 mm≤Dc≤4 500 mm。
(9)
(10)
对修正后的关联式进行数值验证,结果见表5。可以看出,在适用范围内,修正后的关联式与模拟值吻合很好,误差均在4%以内,可用于计算弓形截面螺旋管的Nu和f。

表5 关联式的验证
3 结语
(1)在相同的体积流量下,圆心角α小于180°的弓形截面管Nu均大于半圆形截面管,说明弓形截面有利于提高管内流体的换热性能。但与此同时,管内流动损失也会增加。
(2)相比于截面圆心角α为180°的半圆管,弓形截面螺旋管的综合性能评价因子PEC均大于1,说明弓形截面管子具有更好的综合换热性能,且α越小,管子综合换热性能越好。α为90°时,PEC可达α为180°时的1.18倍。适当减小弓形截面螺旋管截面圆心角,可以提高螺旋管综合换热性能。
(3)换热量和体积流量一定时,采用α越小的弓形截面螺旋管,越能节省材料。与α为180°的半圆管相比,采用α为90°的弓形截面螺旋管,材料消耗可减少约71.6%,显著降低了制造成本。
(4)考虑管截面圆心角对Nu和f的影响,拟合得到了计算弓形截面螺旋管Nu和f的关联式,数值验算表明相对误差在4%以内,为弓形截面螺旋管夹套的工程应用奠定了工艺设计基础。
(5)本文的研究表明,常用的半圆管夹套并不是最佳选择,圆心角小于180°的弓形截面管传热效率更高,综合性能更佳,也更节省材料。另外,相比于半圆管夹套,弓形截面管夹套更容易制造。因此,结合本文提出的弓形截面螺旋管Nu和f关联式,弓形截面螺旋管夹套应有较大的应用前景。
