最大化独立有效分类信息率的属性选择

柳 叶，代建华+，陈姣龙

1.湖南师范大学 智能计算与语言信息处理湖南省重点实验室，长沙410081

2.湖南师范大学 信息科学与工程学院，长沙410081

随着科学技术的迅猛发展，人们面对的数据集往往是复杂且庞大的。在高维数据中存在着大量的冗余属性，这给数据分析、机器学习带来诸多干扰信息，从而导致学习效率低、分类效果差和计算量大等不利影响。因此，属性约简具有重要的应用价值。

粗糙集理论是波兰学者Pawlak提出的一种研究信息系统的不确定性和不完备性的有力工具[1]。该理论已经被广泛地应用于不确定性度量、规则提取和属性约简等方面[2]。在粗糙集理论模型中，现有的属性选择方法大致可以分为三类：（1）基于上、下近似算子的属性选择方法[3-7]；（2）基于差别矩阵的属性选择方法[8-9]；（3）基于熵理论的属性选择方法[10-21]。

在熵理论中，互信息作为一种度量数据相关性的有力工具，被广泛地应用于属性选择之中。目前基于互信息的属性选择方法可大致地分为两种策略：一是最大化待选属性所能提供的分类信息；二是最小化待选属性所带来的冗余信息。然而，最大化待选属性所提供的分类信息并不意味着冗余信息就一定少，反之亦然。实际上，在现有的属性选择方法中，不难发现与决策密切相关的属性之间存在着冗余的情况并不少见。同样地，在最小化冗余信息的同时，可能一些方法更倾向于选择与决策相关性较低的低冗余属性。现有的方法很难有效地衡量属性所提供的分类信息和冗余信息，而且很少有方法考虑到新增待选属性对已选属性所保留的分类信息的影响。

因此，本文首先通过互信息定义了有效分类信息率，并提出了基于有效分类信息率的属性选择策略（attribute selection based on effective classification information ratio，ASECIR）。其次考虑到新增待选属性对已选属性所保留的分类信息的影响，进一步构造了独立有效分类信息率的概念，并提出了基于独立有效分类信息率的属性选择策略（attribute selection based on independent-and-effective classification information ratio，ASIECIR）。最后通过实验验证了本文工作的有效性。

本文的主要贡献如下：

（1）提出了基于有效分类信息率和基于独立有效分类信息率的两种属性选择方法；

（2）提出了有效分类信息率的概念，有效分类信息率能有效地评估待选属性所能提供的分类信息，一定程度上也对自身与类之间的冗余信息进行了评估；

（3）提出了独立有效分类信息率的概念，有机地将待选属性所提供的新增有效分类信息和已选属性保留的有效分类信息与冗余信息相结合，对待选属性的重要性评价更加合理。

1 相关工作

定义1（决策信息表DIS）[22]给定一个四元组＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维的样本集合；C={c1,c2,…,cm}为m维的条件属性集合，D表示决策属性；表示属性的值的集合，Vb是一个给定的属性b的值域；f是一个映射函数，U×C∪D→V满足：∀b∈C∪D,xi∈U，有f(xi,b)=Vb。称该四元组为一个决策信息系统，简称DIS（decision information system）。

互信息是熵理论中十分重要的信息度量结构，可以有效地描述两个变量之间的关联。互信息可以定义如下形式：

其中，H(P)和H(P|Q)分别表示相关变量的信息熵和条件熵。当公式中的变量P、Q分别表示决策属性和条件属性时，I(P;Q)则表示条件属性Q包含决策属性P的分类信息质量，即共享的有效分类信息量。另外，当P、Q都表示两个任意的条件属性时，I(P;Q)则表示条件属性P、Q所共有的信息量，即冗余信息量。

基于互信息的特点，学者们将互信息广泛地应用于属性选择中，用来评价属性之间的相关性程度。文献[10]提出了基于联合互信息的属性选择方法（joint mutual information，JMI）：

文献[11]提出了一种基于对称相关性的双输入对称相关属性选择方法（double input symmetrical relevance，DISR）。文献[12]利用联合互信息提出了规范化最大联合互信息属性选择（normalized joint mutual information maximization，NJMIM）：

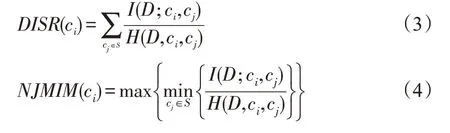
为了提高待选属性在自身信息量中的比重，文献[13]利用互信息提出了一种信息增益率的启发式属性选择算法（GainRatio）：

文献[14]设计了一种基于互信息的属性贪心选择算法（mutual information feature selection，MIFS）。文献[15]通过加权的方式评估待选属性与决策标签之间的互信息，提出了改进的属性选择方法（mutual information feature selector under uniform information distribution，MIFSU）。文献[16]提出了最小冗余最大相关属性选择方法（maximum relevancy minimum redundancy，mRMR）。文献[18]引入平均归一化互信息作为属性间冗余信息的度量方法，提出了一种归一化互信息属性选择方法（normalized mutual information feature selection，NMIFS）：

上述MIFS、MIFSU、mRMR 和NMIFS 的共同特点是，都考虑到了待选属性与已选属性之间的冗余信息，但忽视了对待选属性和已选属性与决策标签之间的类相关信息的考察，即多元互信息。

I(D;ci;cj)=I(D;ci)+I(D;cj)-I(D;ci,cj) （10）

公式描述了两个属性与决策类之间的关联，当某个属性cj被选中时，此时I(D;ci;cj)可以表示为已选属性cj关于决策属性提供的有利于分类的信息。而对待选属性ci而言，I(D;ci;cj)则表示待选属性ci所提供的联合分类信息对决策D来说是冗余的信息量，也称之为类相关冗余信息。

文献[17]利用多元互信息引入类相关冗余的概念，并构造了一种条件信息属性选择算法（conditional informative feature extraction，CIFE）。文献[19]提出了一种最大相关和最大独立的属性选择方法（maxrelevance and max-independence，MRI）：

现有的方法对于属性的相关性和冗余性分析存在着一定的局限性。MIFS、mRMR、MIFSU、NMIFS只关注属性间的冗余，而忽视了待选属性和已选属性与决策类之间的类相关信息。另外，CIFE、GainRatio和NJMIM 在评价待选属性的重要性时，忽视了已选属性对决策类的贡献度。换句话说，只着重考虑待选属性所提供的新增分类信息，而忽视了增加待选属性后对已选属性所保留的有效分类信息的影响。

从上述分析来看，该如何分析待选属性所提供的分类信息和冗余信息，以及新增待选属性对已选属性所保留的分类信息的影响是基于互信息的属性选择方法重点关注的问题。

2 基于互信息的独立有效分类信息率

本章将引入有效分类信息率和独立有效分类信息率的概念。

定义2（有效分类信息率）给定一决策信息系统DIS=＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维样本集合；C={c1,c2,…,cm}为m维条件属性集合，D表示决策属性。已知S为已选属性集(S≠∅)，且S⊆C。假设ci∈C-S为待选属性，则待选属性ci关于决策D所提供的有效分类信息率（effective classification information ratio，ECIR）可定义如下：

ECIR主要关注的核心问题是待选属性能提供多少新增的分类信息。待选属性ci新增的分类信息(I(D;S∪{ci})-I(D;S))在它与决策类D所共有的互信息中的占比越大，说明该属性所提供的新增有效分类信息越多，且与已选属性所共有的类相关信息相对较低。ECIR从理论上有效地将待选属性提供的分类信息和类相关冗余信息统一，有利于寻找较高分类信息和较低类相关冗余的属性。

为了便于理解，通过一个图来进一步说明上述定义，如图1所示。图1描述的是候选属性和已选属性关于决策类之间的关系的Venn 图，其中黑色阴影部分表示待选属性提供的新增有效分类信息，红点部分表示待选属性和已选属性的类相关冗余信息。假设ck、ck+1表示两个待选属性，S代表已选属性子集。属性ck的黑色阴影部分面积表示待选属性ck关于决策类所提供的新增有效分类信息(I(D;S∪{ck})-I(D;S))，红色阴影部分表示ck和属性子集B关于决策类的类相关冗余信息(即多元互信息，I(D;S;ck))。另外，属性ck+1与决策类间不存在类相关冗余信息，即有I(D;S;ck+1)=0 且I(D;S∪{ck+1})-I(D;S)=I(D;ck+1)。

图1 Venn图（待选特征和已选特征关于决策类的联系）Fig.1 Venn diagram(relationship between candidate and selected attributes about decision-class)

假设I(D;S∪{ck})-I(D;S)=I(D;ck+1)，即在图1中属性ck、ck+1的黑色阴影部分的面积是相等的。换句话说，属性ck、ck+1可提供的有效分类信息量是等同的。在这种情况下，现有的属性选择机制很难做出合理的判断。例如MIFS、MIFSU、mRMR和NMIFS在过度强调属性间的冗余信息时，权重的取值会影响到评价指标倾向于选择哪个属性。当权重越大时，评价指标更倾向于选择属性ck+1，反之，则倾向于选择属性ck。再比如属性选择指标CIFE，当已选择的属性只有一个时，CIFE评估属性ck、ck+1的重要性是等同的，此时CIFE会根据序号优先级，直接选择ck。

然而，定义的ECIR 却能缓解这种现象的发生。根据定义2，可分别计算出待选属性ck、ck+1的有效分类信息率：ECIR(ck+1;S;D)＞ECIR(ck;S;D)，说明待选属性ck+1提供的有效分类信息率大于待选属性ck。

考虑到ECIR 只关注待选属性所提供的有效分类信息，而忽视了加入待选属性后对已选属性所保留的分类信息的影响，因此，本文进一步提出了独立有效分类信息率的概念。

定义3（独立有效分类信息率）给定一决策信息系统DIS=＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维的样本集合；C={c1,c2,…,cm}为m维的条件属性集合，D表示决策属性。已知S为已选属性集(S≠∅)，且S⊆C。假设ci∈C-S为待选属性，则独立有效分类信息率（independent-and-effective classification information ratio，IECIR）可定义如下：

IECIR 有效地将待选属性所提供的分类信息和冗余信息以及新增待选属性对已选属性所保留的分类信息之间的关联进行了统一。IECIR 有助于增强属性的有效分类信息和冗余信息的取舍。通过最大化待选属性和已选属性的有效分类信息率，在一定程度上也降低了属性的冗余性，进一步提高了属性子集的整体识别能力。

3 属性选择方法

在前文，本文分析了现有方法所存在的问题，即无法权衡待选属性所提供的分类信息和冗余信息，以及新增待选属性时对已选属性所保留的分类信息的影响。针对这些问题，本文提出了有效分类信息率ECIR和独立有效分类信息率IECIR的概念。本章依据上述定义的ECIR 和IECIR，提出了两种属性选择方法。

3.1 基于有效分类信息率的属性选择方法

定义4（特征重要性评估函数1）给定一决策信息系统DIS=＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维的样本集合；C={c1,c2,…,cm}为m维的条件属性集合，D表示决策属性。假设已知S为已选属性子集，ci为待选属性且ci∈C-S。在基于有效分类信息率的属性选择方法下，待选属性ci的重要性的计算如下所示：

本文通过式（15）来计算候选属性的重要性，Sig1(ci;S;D)值越大说明该候选属性越重要。

根据定义4，本文设计了一个启发式属性选择算法，具体的实现步骤在算法1中给出。

算法1基于有效分类信息率的属性选择算法

输入：一个决策信息系统DIS=＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维的样本集合，C={c1,c2,…,cm}为m维的条件属性集合，D表示决策属性。

输出：S为已选属性子集。

首先，计算等价类的时间复杂度为O(|U|2|C|)。因此，计算互信息等熵度量的时间复杂度为O(|U|2|C|+|U|2)。进而，属性选择算法的时间复杂度为O(|S||C|(|U|2|C|+|U|2))。

3.2 基于独立有效分类信息率的属性选择方法

考虑到ASECIR 只关注待选属性所提供的新增的有效分类信息，而忽视了加入待选属性后对已选属性所保留的分类信息的影响，本文进一步提出基于独立有效分类信息率的属性选择方法。

定义5（特征重要性评估函数2）给定一个决策信息系统DIS=＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维的样本集合；C={c1,c2,…,cm}为m维的条件属性集合，D表示决策属性。假设已知S为已选属性子集，ci为待选属性且ci∈C-S。在基于独立有效分类信息率的属性选择方法下，待选属性ci的重要性定义如下所示：

若S=∅，Sig2(ci;S;D)=I(D;ci)/H(D)。

通过式（16）来计算候选属性的重要性，Sig2(ci;S;D)值越大说明该候选属性越重要。

根据定义5，本文设计了一个启发式属性选择算法，具体的实现步骤在算法2中给出。

算法2基于独立有效分类信息率的属性选择算法

输入：一个决策信息系统DIS=＜U,C∪D,V,f＞，其中U={x1,x2,…,xn}为n维的样本集合，C={c1,c2,…,cm}为m维的条件属性集合，D表示决策属性。

输出：S为已选属性子集。

首先，计算等价类的时间复杂度为O(|U|2|C|)。因此，计算互信息等熵度量的时间复杂度为O(|U|2|C|+|U|2) 。进而，属性选择算法的时间复杂度为O(|S||C|(|U|2|C|+|U|2))。与属性选择算法GainRatio的时间复杂度较为相近，但总体要低于mRMR、MIFS、CIFE、MRI 等具有代表性的属性选择算法的时间复杂度，其原因在于mRMR、MIFS 等方法的属性重要性计算中需要重复计算已选属性的互信息。

4 实验与结果

本章将通过与现有的方法进行对比实验，进一步说明本文提出的两种属性选择方法（ASECIR 和ASIECIR）的合理性。

4.1 实验准备

为了综合地对比ASECIR和ASIECIR的有效性，本文选取8种具有代表性的基于互信息的属性特征选择算法进行实验比较，包括DISR[11]、NJMIM[12]、GainRatio[13]、MIFS[14]、mRMR[16]、NMIFS[18]、CIFE[17]、MRI[19]。用 于本文的实验基准数据均来自UCI数据库，数据集的详细信息展示在表1 中。考虑到部分实验数据是实值型数据，因此采用离散化技术对实值数据进行离散化处理。

表1 基准数据的描述Table 1 Description of benchmark dataset

为了公平地判断所选属性子集的分类精度，本文使用了KNN分类器(K=3)、C4.5分类器以及SVM分类器对所选的属性子集进行10次10折交叉验证，并取10次结果的平均值作为算法分类精度的评估值。

本文所有的实验都是在相同的软硬件环境下进行的。软硬件环境：Windows 7系统、Intel®CoreTMi5-5200U CPU@2.20 GHz处理器、8.00 GB内存、MATLAB2019a、WEKA 3.8。

4.2 实验和结果

表2～表4 分别展示了在KNN(K=3)、C4.5 以及SVM 分类器下分类精度的实验结果，每一行中的最优分类精度值用粗体以及下划线突出显示，最后两行代表每个算法在所有基准数据下的平均分类精度（Avg.Acc）和平均序值（Avg.Rank）。

在表2 中，ASIECIR 和ASECIR 在所有方法中取得了最好和次优的平均分类精度，分别达到了83.36%和82.66%，且ASIECIR 的平均序值低于其他方法。在表3 中，ASIECIR 和ASECIR 在所有数据集上获得了最好和次优的次数最多，且两种方法的平均分类精度值（82.13%、81.78%）高于其他方法，ASIECIR 的平均序值也优于其他方法。此外，在所有对比方法中，除MRI 之外的其他对比方法的平均分类精度均低于80.00%。在表4 中，ASIECIR 和ASECIR 在所有方法中取得了最好和次优的平均分类精度，分别达到了81.38%和81.01%，且ASIECIR的平均序值低于其他方法。此外，在所有对比方法中，MRI 和DISR 方法的总体表现优于其他6 种对比方法。

表2 在KNN分类器上不同方法的分类精度Table 2 Classification accuracy with different methods by KNN classifier

表3 在C4.5分类器上不同方法的分类精度Table 3 Classification accuracy with different methods by C4.5 classifier

表4 在SVM分类器上不同方法的分类精度Table 4 Classification accuracy with different methods by SVM classifier

从上述结果总结如下：（1）ASECIR 和ASIECIR的平均分类精度高于其他对比算法，且ASECIR低于ASIECIR。此外，在对比方法中，MRI 的总体性能虽然低于本文所提出的两种属性选择算法，但优于其他对比方法。由此可以发现，本文设计的独立分类信息率能够有效地提高特征选择的性能；（2）ASIECIR的平均序值低于其他方法，且ASECIR和ASIECIR在所有方法中是获得最优结果最多的两种方法，其中ASIECIR 的表现更好。总体取得了较为理想的分类性能。

综合上述分析，可以发现在对特征的相关性和冗余性的分析研究上，本文所设计的有效分类信息率和独立有效分类信息率对待选属性的重要性评估总体上表现得更为出色，也从实验上进行验证所提出的理论模型的合理性。

为了进一步分析所提出的属性选择方法与其他方法之间分类性能效果上的差异性，本文利用在三种分类器上得到的分类结果进行Bonferroni-Dunn后续检验测试。Bonferroni-Dunn 测试方法是通过比较对比方法与一个核心方法的平均序值差值和临界差值的大小来分析对比方法与核心方法之间的关联。在该实验中，以ASIECIR为核心方法和对比的8种方法进行Bonferroni-Dunn后续检验。临界差值（critical difference，CD）的计算如下公式所示：

其中，K表示实验方法的个数（K=9），N为实验数据集的个数（N=13）。pα表示在显著性水平为α下的临界值。在本文中，首先令显著性水平α=0.05，通过文献[23]可知pα=2.724，故CDα=2.926。若某个方法的平均序值与ASIECIR的平均序值的差值越大，则说明ASIECIR 的效果显著优于该方法的程度越大。特别地，若该方法的平均序值与ASIECIR 的差值超过CD值，则说明ASIECIR的性能效果显著优于该方法。

Bonferroni-Dunn 检验的相关实验结果展示于图2中，其中图（a）～（c）分别表示在KNN、C4.5以及SVM分类器上的Bonferroni-Dunn检验结果。从图2（a）中可以发现ASIECIR 方法的性能显著优于CIFE。除CIFE以外的其他对比方法虽然都与ASIECIR在一个CD 值范围内，但距离最近的对比方法NJMIM 和MRI 仍与ASIECIR 存在着较大的差异，差值至少超过1.5。由此进一步说明ASIECIR 的性能优于其他对比方法的程度很大。在图2（b）中，ASIECIR 的性能优于对比方法MIFS、CIFE 和NMIFS。同时，距离最近的对比方法GainRatio 与ASIECIR 方法的平均序值的差值至少超过1.5。在图2（c）中，ASIECIR 方法在SVM 分类器上的性能显著优于对比方法NJMIM和MIFS。其中，距离ASIECIR方法最近的对比方法NMIFS和MRI方法的平均序值仍与ASIECIR方法有着较为明显的差距。

图2 Bonferroni-Dunn检验Fig.2 Bonferroni-Dunn test

综合上述结果分析可以发现，本文所提出的ASIECIR 与现有的一些属性选择方法之间存在着一定的性能差异，且ASIECIR 表现总体更优。由此说明，本文所设计的独立分类有效信息率的属性重要性评估函数在一定程度上具备很好的区分属性相关性和冗余性的能力，可以作为一种可行的属性重要性评估策略用于属性选择的研究中。

5 结束语

本文提出了基于有效分类信息率的属性选择方法，可以有效地选择能提供大量有效分类信息同时携带较少冗余信息的待选属性。考虑到新增的待选属性对已选属性所保留的分类信息的影响，进一步提出了基于独立有效分类信息率的属性选择方法。实验结果表明，所提出的属性选择方法在选择重要属性的机制、分类精度上都明显地优于许多现有的属性选择方法。在未来的工作中，将进一步深入探讨更复杂情况下（例如，动态的决策信息系统和存在决策部分缺失的数据）的属性相关性和冗余性的关联，并设计出有效的属性选择方法。