基于距离优势关系的高维多目标进化算法

顾清华，徐青松，李学现

1.西安建筑科技大学 管理学院，西安710001

2.西安建筑科技大学 资源工程学院，西安710001

3.西安市智慧工业感知计算与决策重点实验室，西安710001

在实际生活中，如无人机任务规划、雷达的波形设计等问题往往是高维多目标优化问题[1]。多目标优化进化算法是解决这些问题的重要手段，但是现有的多目标优化算法在处理高维多目标问题上会面临维数诅咒难题。传统的Pareto 支配关系很难有效区分非支配层级，导致种群的大多数个体都处于非支配层级。为了解决这一问题，许多学者从增大选择压力出发提出了新的方法来克服这一问题，根据增大选择压力方式的不同，这些方法大致分为三类：

第一种策略是发展新的优势关系，主要思想是增加两个候选解在多目标优化问题上的可比性。Sato等提出了控制解的支配区域[2]的方法，使用三角函数通过设定参数来改变目标函数的适应度值，进而使解的优势区域发生改变。虽然控制优势区域能增强算法的选择压力，但是参数难以确定，不恰当的参数设定会降低算法的多样性。定义模糊优势关系，在L-支配[3]中通过比较优劣解的个数以及目标函数的范数来比较个体间的优势关系。在(1-k)-支配[4]中通过预设的参数k比较劣解集及相等解的个数来确定个体的优势关系。在模糊支配[5]通过高斯公式转换两个个体的表现值，表现值相乘得出的值相比较来定义优势关系。这种方式的好处在于能有效化解目标维度的增加带来的Pareto优势互相抵消，但是这种方式并不能有效保证算法的收敛性。

第二种策略是将原有的Pareto 优势与特定的选择方式结合。通过Pareto 优势来进行初次比较淘汰劣解后再进行二次选择。例如KnEA[6]在二元锦标赛中结合支配关系引入拐点准则和加权距离，利用非支配解拐点的偏向来提高算法的收敛性。在VaEA[7]中通过最大角优先原则与消除差解原则选择收敛性与分布性更好的解参与进化，但是这使得算法不能很好解决规则Pareto前沿面问题。

第三种策略是将传统的Pareto 优势与基于分解的思想相结合，既保留了Pareto 支配的支配层级，又结合了基于分解的适应度值和独立子空间等特性。在MOEADD[8]中保留基于分解的子空间特征，通过引入Pareto支配关系增强更新过程中算法的收敛性，并且设计种群局部密度维护算法多样性。在RPDNSGA-Ⅱ[9]中提出了一种基于分解的支配关系，并且引入参考点。结合Pareto 支配并按照参考点关联候选解的数量，以及计算候选解到理想点的距离来判断解的优劣。

虽然上述三种策略能一定程度上增强算法的性能，但是这些方法大多需要预先设定合适的参数，而且较难维持算法在高维多目标问题上的多样性，使得大多数的非支配解集聚集在前沿面上的一小部分区域。基于存在的问题，为了增强算法在高维目标空间中的多样性，本文提出一种新的支配关系。首先，在非支配排序阶段不仅考虑了收敛性，同时进行了多样性的维护，而且所提出的距离优势关系不需要预先定义参数。其次，结合所提出的距离优势关系对VaEA 算法进行了改进，不仅提升了VaEA 算法在高维多目标问题上的性能，而且提升了VaEA算法解决规则Pareto前沿面问题的能力。最后，通过一系列测试问题验证所提出支配关系的适用性。

1 相关背景

1.1 高维多目标优化问题

高维多目标优化问题是指目标维度超过4 的多目标优化问题，不失一般性，以最小化为例，高维多目标的一般表现形式如下：

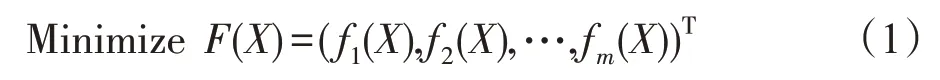
其中，m≥4，Ω是决策空间，x=(x1,x2…,xn)∈Ω是决策变量。

1.2 VaEA算法

VaEA算法是由Xiang等于2017年提出的一种基于向量角的多目标进化算法，VaEA算法的基本框架与大多数基于支配关系的算法类似，图1给出了VaEA算法的流程图。首先，在决策空间中随机初始化生成N个个体的种群。然后，根据每个个体的适应值选择更优的个体进入交配池。在接下来的操作中，通过应用交叉和变异操作来生成一组子代解Q，并合并父代与子代种群。最后，使用Pareto支配关系对合并后的种群进行非支配排序，按照非支配层级由低到高加入外部档案，并采用环境选择操作使外部档案的种群规模为N。VaEA算法的核心是设计了最大角优先原则与消除差解原则，其中最大角优先原则是指，优先选择临界层中与外部档案中个体关联角度最大的个体加入外部档案，这是为了增强种群的多样性。另一方面，消除差解原则是为了维护种群的收敛性，将一些收敛性太差的个体剔除，选择与这些差解多样性相似，但是收敛性更好的个体加入外部档案，直到外部档案的种群规模为N。

图1 VaEA算法流程图Fig.1 Flow chart of VaEA algorithm

2 提出算法

2.1 整体框架

本文提出的VaEA-DDR 算法整体框架与VaEA算法一致，区别在于VaEA-DDR算法使用距离优势关系对种群进行非支配排序。算法1给出了具体流程。

算法1VaEA-DDR算法流程

输入：种群P，种群规模N，最大迭代次数Gmax。输出：最终种群P。

2.2 距离优势关系

距离优势关系结合小生境技术[10]，不仅考虑到解的收敛性，同样使解的多样性得到了增强。具体来说，如果解X1距离支配解X2，即X1≺DDRX2，则满足下列条件：

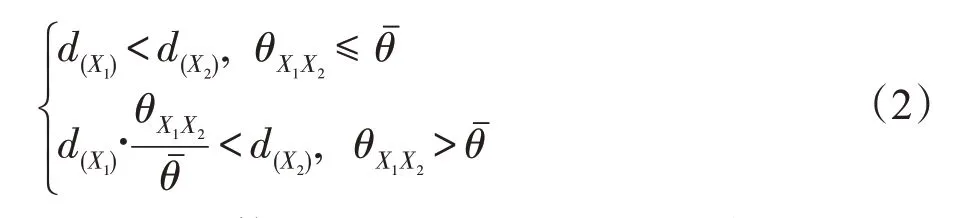
其中，d(X)是个体到理想点的欧氏距离，将这一距离作为适应度值来选择更优的解。表示两个候选解的目标值之间的夹角，即：

算法2距离优势关系

输入：种群P，种群规模N。

图2 说明了距离优势关系在双目标空间的优势区域。从图中可以看出，解X1的优势区域由两部分组成，在设定的小生境内根据候选解到理想点的距离可以得出区域1，根据式（2）中的第二个公式可以得出另一个优势区域2。解X1与解X2在同一小生境内，比较两个解到理想点的距离可以得出解X1≺DDR解X2。解X1与解Y不在同一小生境内，θX1Y＞，但是根据式（2）中第二个公式可以得出解X1≺DDR解Y。从这里可以看出，某些目标函数值较差的候选解可能会被认为是非支配解，但是在这里并没有试图定义一种新的方式解决这个问题。一方面，这些较差的解还在预设的范围内，而且这些较差的非支配解数量较少，不会影响算法的收敛性；另一方面，如果将这些消除，这些差解将会极大增加距离优势关系的计算复杂度。

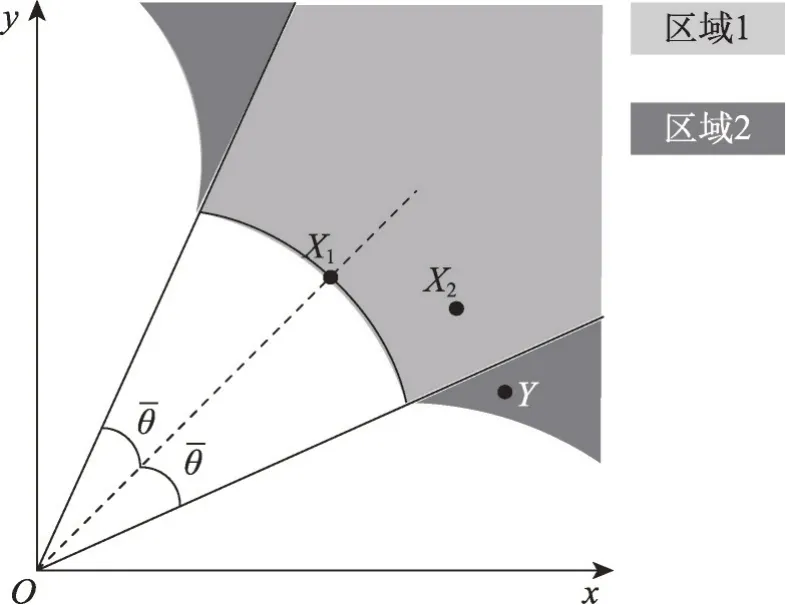
图2 双目标空间中距离优势关系支配区域Fig.2 Dominated area of distance dominancerelationship in dual-objective space

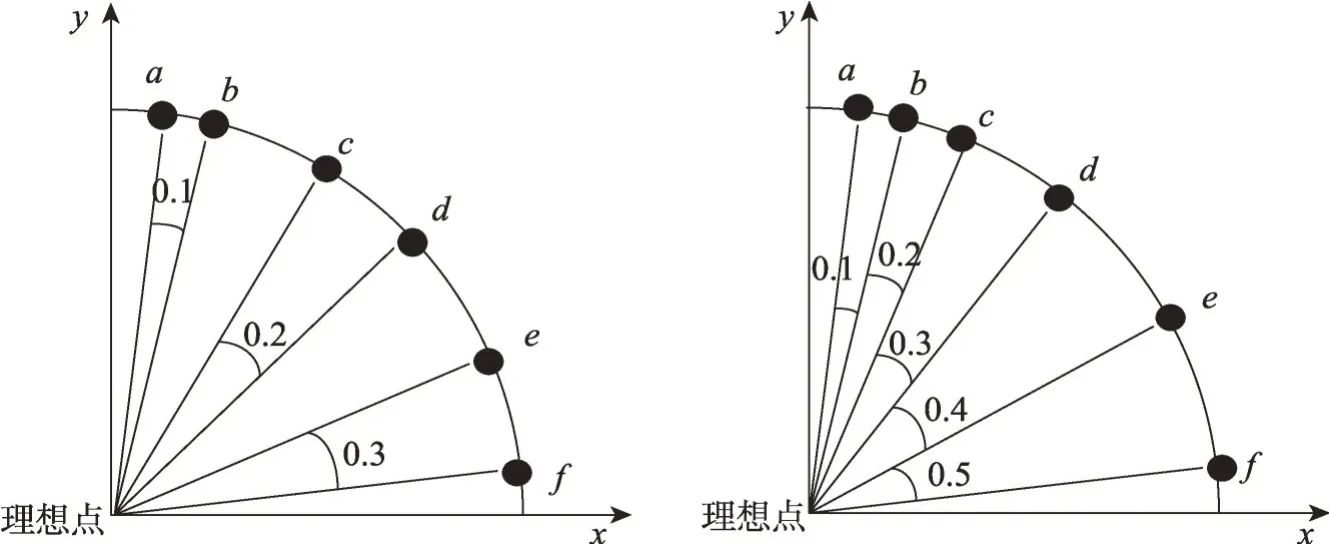
图3 双目标空间中不同种群分布示意图Fig.3 Schematic diagram of distribution of different populations in dual-objective space

3 仿真实验与结果分析

3.1 测试问题与对比算法

为了验证VaEA-DDR算法性能，选取了DTLZ系列测试集进行实验研究。表1 给出了测试问题及其特征。根据目前几个主要的研究方向，选用近年最具有代表性的算法作为对比算法，包括NSGA-Ⅲ[11]、MOEADD[8]、MOMBI-Ⅱ[12]、RPD-NSGA-Ⅱ[9]、NSGA-Ⅱ-SDR[10]、VaEA[7]。

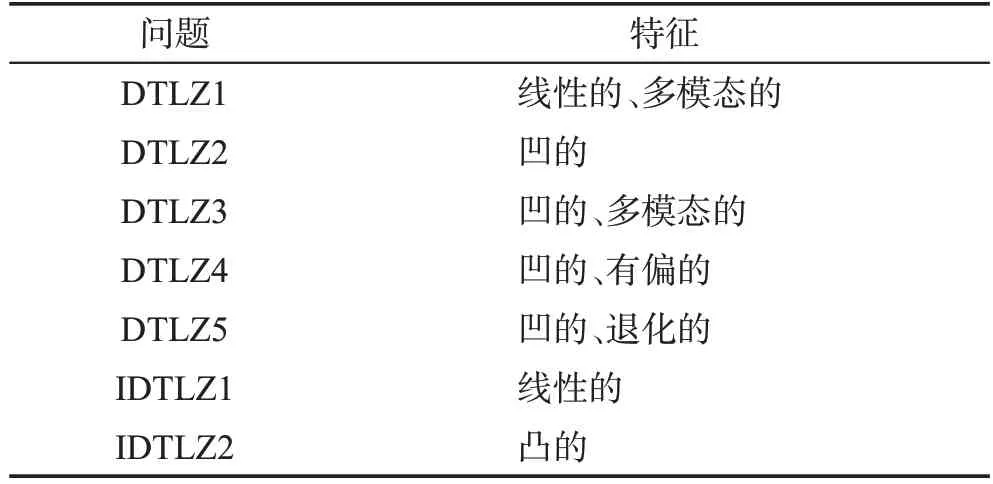
表1 测试问题及其特征Table 1 Test problems and their characteristics

3.2 性能评价指标

文中采用的性能评价指标主要有：反转世代距离（inverted generational distance，IGD）[13]，该指标是对收敛性和多样性的综合性评价指标；广义分布（Spread/Δ）[14]，该指标主要评估算法多样性；世代距离（generational distance，GD）[15]，该指标主要评估算法收敛性。

设P为近似集，P*为沿真实帕累托前沿均匀分布的非支配点集，|P*|是P*中解的个数，|P|是P中解的个数，dist(z*,P)是z*与P中最近邻域之间的欧几里德距离。则三个性能评价指标计算公式分别如下：

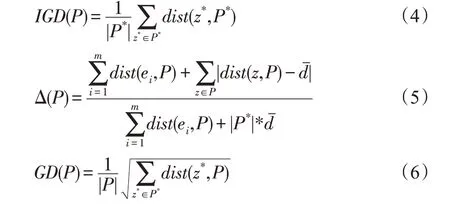
3.3 参数设置

实验过程中涉及的多目标算法存在一些参数需要设定，具体如下：

（1）种群规模：表2 概述了不同数量目标的种群规模N和权重向量的数量。

表2 权重向量的数量和种群规模Table 2 Number of weight vectors and population size

（2）邻域规模：邻域T的大小设置为0.1N。

（3）PBI中的惩罚因子：θ=5.0。

飞机在恐怖的黑暗中又坚持飞行了近两个钟头。一直没有声音的广播突然传出机长的紧急通知：“飞机遇到特大气流，大家忍耐一下，正在联系准备迫降。”不知又过了多久，广播中再次传来了机长的通知，内容大致是：飞机准备迫降在阿拉斯加阿留申群岛的薛米亚美国空军基地。但是这个岛太小，机场不具备降落大型民用客机的条件，跑道不够长，没有足够的照明设施。加上眼下气候恶劣，有大风暴，能见度很低。我们飞机自身的受损情况不明，起落架不知道能不能打开。所以能否安全降落仍是未知数。请大家做好自救准备！

（4）运行次数及终止条件：每个算法在每个测试实例上独立运行30次，算法的终止条件是5、8、10、15目标上算法运行迭代次数分别为200、300、300、500次。

3.4 实验结果分析与讨论

本节给出了VaEA-DDR算法与NSGA-Ⅲ、MOEADD、MOMBI-Ⅱ、RPD-NSGA-Ⅱ、NSGA-Ⅱ-SDR以及VaEA算法对比的实验结果。实验结果为在PlatEMO平台[16]独立运行30 次结果的平均值与标准差。在PlatEMO 中，采用显著性水平为0.05 的Wilcoxon 秩和检验对结果进行分析，“+”“-”“=”分别表示对比算法的结果比提出算法的结果好、差以及在统计学上相似。

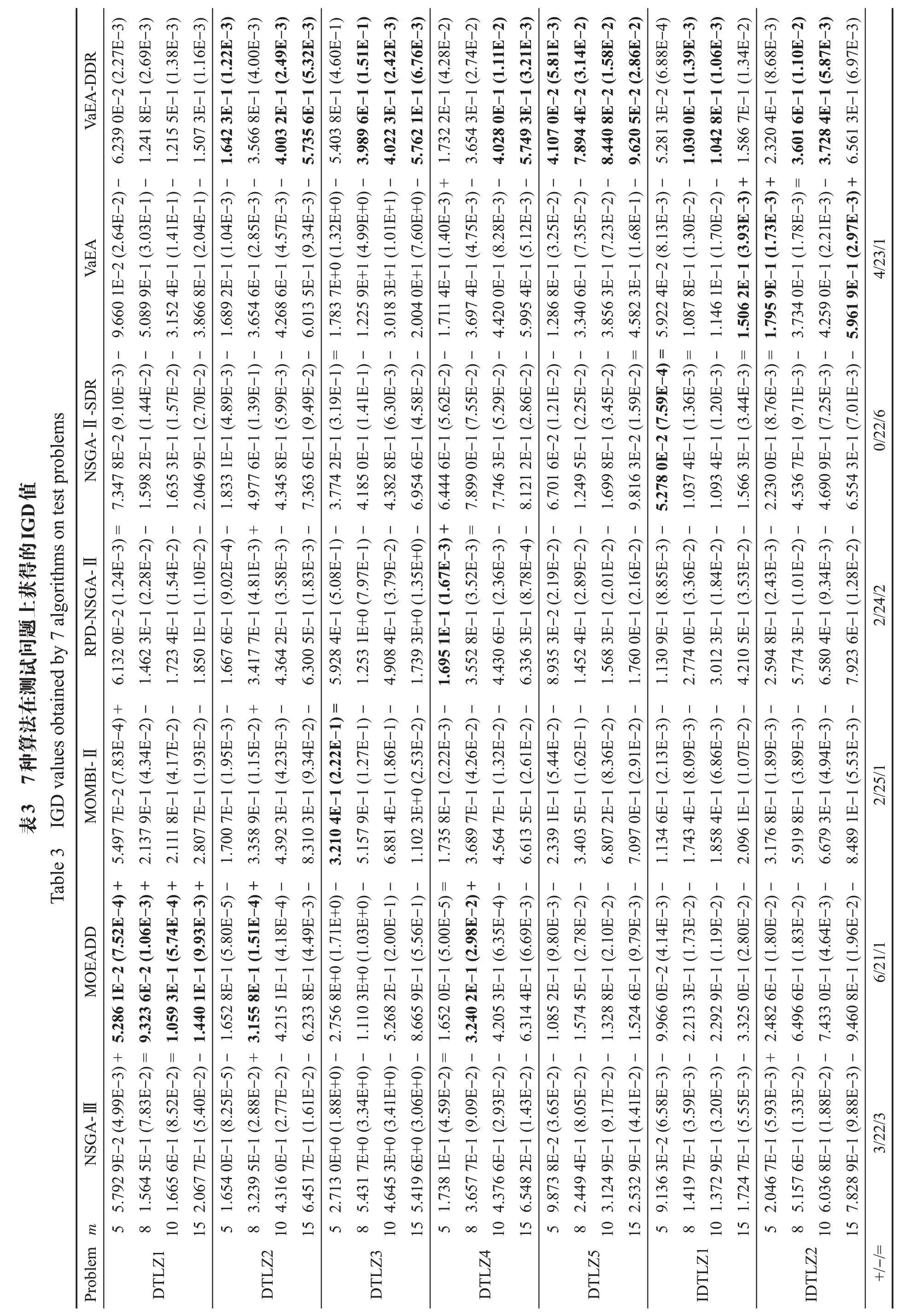
表3 给出了7 种算法在5、8、10、15 目标DTLZ 与IDTLZ测试问题上获得的IGD 平均值与标准差。从表中可以知道，VaEA-DDR算法所取得的最佳IGD值的个数为16 个。比NSGA-Ⅲ、MOEADD、MOMBI-Ⅱ、RPD-NSGA-Ⅱ、NSGA-Ⅱ-SDR以及VaEA取得更佳IGD值的个数分别为22、21、25、24、22、23。

VaEA-DDR 算法在DTLZ1 与IDTLZ1问题上表现不佳，在DTLZ1 测试问题上，MOEADD 算法为表现最佳的算法。在IDTLZ2 问题上，VaEA-DDR 与NSGA-Ⅱ-SDR 算法的IGD 值十分接近。这是因为DTLZ1 与IDTLZ1 都是具有线性Pareto 最优面的测试问题，但是在本文中定义的支配关系通过基于到理想点的距离来选择适应度更好的解，这种支配关系较难判断线性平面上解的收敛程度。这可能会造成在解决具有线性平面的多目标问题时，文中提出的算法较难具有很强的竞争力。

DTLZ2～5 是凹优化问题，从实验结果可以知道VaEA算法表现最佳。为了更直观了解IGD值的变化，图4 给出了7 种算法在15 目标上DTLZ2、DTLZ4、DTLZ5 以及IDTLZ2 的IGD 值变化曲线。从图4（a）中可以看出VaEA-DDR算法最快降至最小值并稳定在最小值，相比VaEA 算法在早期IGD 值收敛更快。MOMBI-Ⅱ算法IGD 值表现最差，NSGA-Ⅱ-SDR 算法的IGD 值出现了明显的波动，虽然在早期算法具有很好的收敛性，但是随着迭代次数的增加IGD 值会迅速增加，这说明NSGA-Ⅱ-SDR算法在迭代过程的早期能很迅速接近最优解，但是可能会出现远离最优解集的情况。从图4（b）中仍可以看出VaEA-DDR算法相对VaEA算法在前期IGD值下降更迅速。

DTLZ5 问题最后会收敛为一条退化曲线，在该问题上改进的VaEA-DDR算法表现出绝对优势。对比VaEA 算法与VaEA-DDR 算法的实验结果可以看出，VaEA算法的性能仅相比MOMBI-Ⅱ算法有优势，这说明本文提出的距离优势关系对VaEA 算法的性能有较大提升。从图4（c）可以看出大部分算法的IGD值出现了明显的波动，其中MOMBI-Ⅱ算法的IGD值一直处于上升趋势，这说明算法形成的解正在远离Pareto前沿面。NSGA-Ⅲ、RPD-NSGA-Ⅱ、NSGA-Ⅱ-SDR 以及VaEA 算法出现了不同程度的波动，但是VaEA-DDR 算法IGD 值一直处于下降趋势，这说明VaEA-DDR能较好处理退化问题。

IDTLZ2 问题是一个凸优化问题，从实验结果看VaEA-DDR 算法仅在8 目标与10 目标问题上具有最佳的IGD值。从图4（d）可以看出在15目标上VaEADDR 算法IGD 值下降与NSGA-Ⅱ-SDR 算法基本一致，最终仅比VaEA算法略差。这说明在凸优化问题上，文中提出的距离优势关系对算法性能的提升较小。

图4 7种算法在15目标上获得的IGD值变化曲线Fig.4 IGD value change curves of 7 algorithms on 15 objectives

为了检验提出的距离优势关系是否能增强VaEA算法多样性，表4给出了7种算法在5、8、10、15目标DTLZ 和IDTLZ 测试问题上获得的Spread 平均值与标准差。从表4 中可以知道VaEA-DDR 算法具有最佳Spread 值的个数为16，相比6 种对比算法具有更优Spread 值的个数分别为24、24、27、28、21、10。由此可知距离优势关系显著增强了VaEA 算法多样性。

为了检验距离优势关系能否有效保证算法的收敛性，表5 对VaEA 与VaEA-DDR 算法的GD 值进行对比。从表中可以看出，改进后的VaEA-DDR 算法在DTLZ1、DTLZ4 与IDTLZ1 问题上表现出绝对优势，VaEA 算法仅在15 目标DTLZ2，5 目标与8 目标DTLZ3 和DTLZ5 以及IDTLZ2 测试问题上比VaEADDR 具有更好的GD 值。这说明距离优势关系并没有削弱算法的收敛性，在DTLZ1 问题上可以明显看出，距离优势关系有效增强了算法的收敛性。

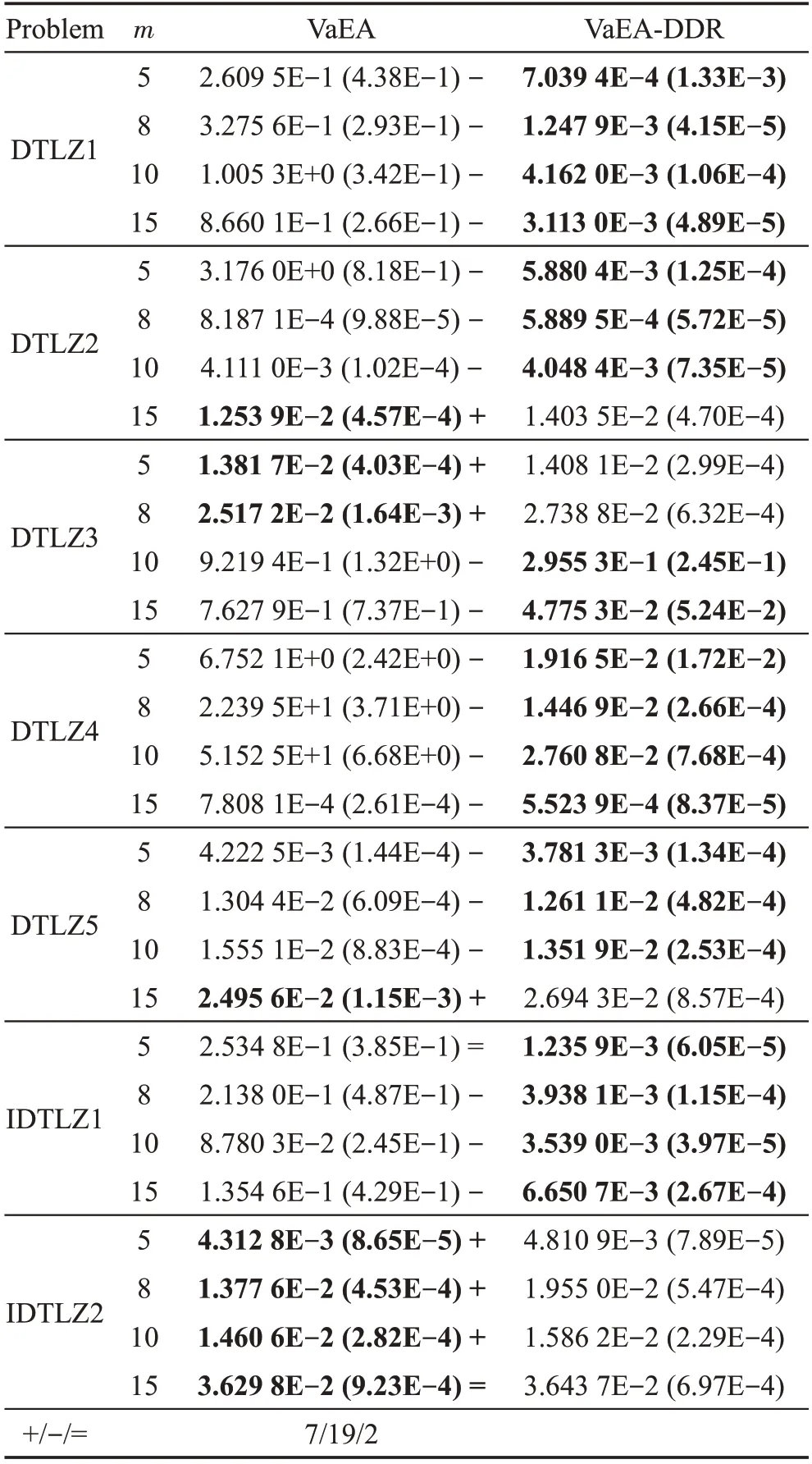
表5 VaEA与VaEA-DDR算法GD值对比Table 5 Comparison of GD values between VaEA and VaEA-DDR algorithms

综上所述，本文提出的距离优势关系极大提升了VaEA算法求解高维多目标问题上算法的多样性，在增强算法多样性的同时有效维护了算法的收敛性。

3.5 汽车碰撞测试实验的实际应用

为了验证改进后的算法在实际应用上的求解性能，在经典的高维多目标汽车碰撞的实际问题[17]上对算法性能进行测试。汽车碰撞问题为9 目标测试问题，决策变量的个数为11个，包括汽车相关构件的厚度、材料性质等。最大的迭代次数为800 次，种群大小设置为11d-1，d为决策变量数量。在实际问题上运行20 次得到的IGD 与HV 平均值用来评估实验结果。注意，计算IGD值时，所有算法得到的非支配集作为参考集；计算HV 时，所有算法得到的非支配集的最差目标函数加上一个小阈值作为参考点。表6 给出了7 种算法在实际问题上获得的IGD 和HV值。从实验结果看，改进后的算法获得了最佳的IGD和HV值，相比原算法有一定的提升。这说明在实际问题上，使用距离优势关系改进后的算法仍能具备良好的求解性能。

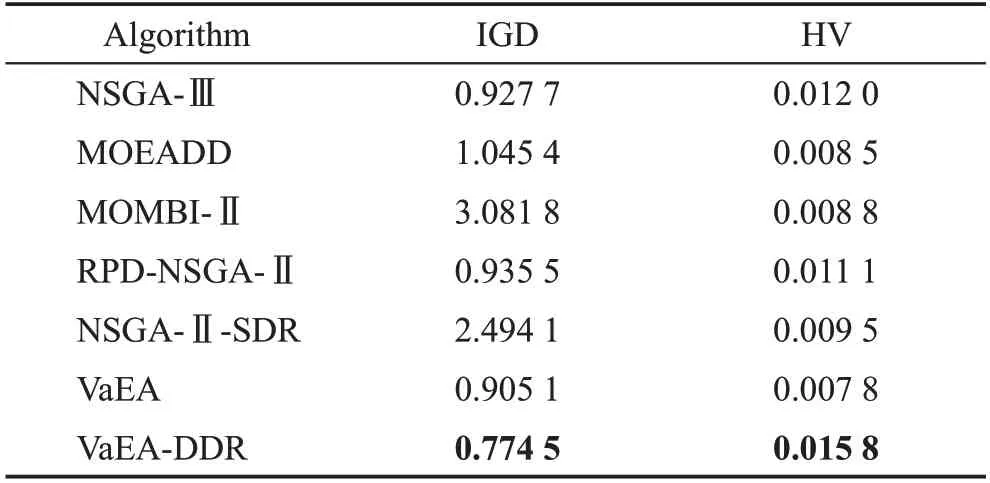
表6 7种算法在汽车碰撞实验获得的IGD与HV值Table 6 IGD and HV values obtained by 7 algorithms in car crash experiment

3.6 距离优势关系适用性验证

为了验证所提出的距离优势关系的适用性，本节给出了结合距离优势关系改进的NSGA-Ⅲ算法的实验对比。表7 给出了NSGA-Ⅲ与NSGA-Ⅲ-DDR算法在PlatEMO 平台独立运行30 次后得到的IGD值、Spread值以及GD值。

从表7 中可以知道，改进后的NSGA-Ⅲ-DDR 算法具有最优的IGD值、Spread值以及GD值最佳的个数为23、26、15。尤其是从Spread 值上可以看出，改进后的NSGA-Ⅲ-DDR 算法基本上都具有最佳值，NSGA-Ⅲ算法仅在5目标的DTLZ1问题与15目标的DTLZ5 问题上具有更优的Spread 值，这再次验证了距离优势关系能显著提升算法的多样性。同时，从GD 值上可以看出，两种算法均具有一半的最优值，这说明了距离优势关系能有效保证算法的收敛性。综合上述分析，说明了距离优势关系对NSGA-Ⅲ算法的性能同样有提升，具有较强的适用性。

4 结束语

为了增强算法在高维目标空间的多样性，本文提出了一种距离优势关系。首先，通过计算候选解到理想点的距离作为适应度值选择更优解，能保证求解过程中算法的收敛性。其次，通过构建的小生境选择技术，保证了在同一小生境内只保留一个最优解，能在非支配排序阶段有效加强算法的多样性。基于所提出的优势关系对VaEA算法进行改进，在DTLZ 与IDTLZ 测试问题上进行对比实验。从实验结果可以知道，改进的VaEA-DDR 算法取得最佳IGD 值与Spread 值的个数分别为16、16，并且在多样性方面具有显著性优势。同时在NSGA-Ⅲ算法上验证了所提出距离优势关系的适用性，实验结果表明本文提出的距离优势关系具有良好的适用性。在汽车碰撞实验中，改进后的算法能取得最优的表现，这说明使用距离优势关系改进的算法能应用于实际问题求解。

虽然从实验结果来看距离优势关系对算法的性能有较大提升，但是目前算法不能非常有效区分依据距离优势关系划分的非支配层级。在后续的研究过程中可以进一步完善研究算法的选解过程，提升距离优势关系的适应性。