基于特征加强的异构网络潜在摘要模型

徐正祥，王 英，汪洪吉，王 鑫+

1.吉林大学 计算机科学与技术学院，长春130012

2.符号计算与知识工程教育部重点实验室，长春130012

3.吉林大学 人工智能学院，长春130012

图摘要是图挖掘领域中处理大规模图数据的一项非常重要的技术，其目的是产生原始图的一种紧凑表示，用于压缩和简化数据以实现高效计算、高效查询等。例如，将原图的多个节点映射到一个超节点，将原有的边映射到一个超边上，输出一个超图摘要，以实现对原图的压缩，同时可以通过错误边界调整摘要大小，进而实现在摘要图中的高效查询。

然而，现实世界中大多数网络都含有多种类型的节点和边，也就是广义上的异构信息网络[1]，例如，在Movie 数据集中有导演、电影、演员等不同类型的节点，这些节点间的关系包括执导、参演等。因此，异构信息网络的复杂性在于其节点和边类型的多样性，以及由此产生的复杂结构和丰富语义，如何在异构网络中获取图的摘要是当前的重要挑战。

传统的摘要方法[2]通常将节点映射到超节点从而导出超图，并不能导出节点表示。为了将节点表示与网络摘要融合起来，本文提出了基于特征加强的异构网络潜在摘要模型FELS。不同于传统的摘要方法，FELS 模型的目标是在潜在空间中获取节点的低维表示，使得它独立于图的大小，即图节点和边的数量。FELS 模型不仅能够获取潜在的图摘要，还能够获取节点的表示。主要贡献如下：

（1）利用多种关系算子捕获节点间不同结构信息，通过迭代的方式增强对节点邻域结构的学习。同时，提出桶映射概念，将不同图属性映射到不同桶，解决了特征偏斜问题。

（2）FELS 模型的输出大小独立于网络数据的大小（节点数量），仅与数据的复杂度有关，并且可以控制摘要大小，以及动态推导出节点表示，以达到高精度和高压缩的选择。

（3）FELS模型通过减少对重复特征的处理，降低了模型复杂度，减少了计算内存，有助于实现对更大数据集的处理。

（4）通过将FELS 模型应用到异构网络数据集上，在链路预测任务上，与最先进的方法相比，FELS精度提升了近4个百分点，在空间占比上，FELS具有更明显的优势。

1 相关工作

1.1 网络表示

网络表示方法在广义上可分为三类：（1）基于矩阵分解方法[3]。De Ridder等人[4]假设每个节点在潜在空间内都是其邻节点的结合，将约束最优化问题简化成特征值问题，截取较大特征值对应的特征量作为输出；Belkin等人[5]保证当权重矩阵的权值较高，所对应的两个节点在嵌入空间的距离较近，将较小的正则化的拉普拉斯矩阵特征值所对应的特征向量作为输出；Ahmed 等人[6]分解了图的邻接矩阵，最小化了损失函数；Cao等人[7]通过考虑全局结构信息，提出了一种学习加权图节点向量表示的新模型；Ou等人[8]通过最小化相似度矩阵与顶点嵌入矩阵的距离，并使用奇异值分解（singular value decomposition，SVD）获取节点表示。（2）基于随机游走方法。Perozzi等人[9]利用截断的随机序列表示节点的近邻，然后将得到的序列结合当作自然语言处理中的一个句子作为词向量的输入，进而得到节点表示；Tang 等人[10]为了缓解一阶近邻的稀疏性，考虑了更多的近邻丰富节点的表示，例如，二阶近邻主要考察两个节点的共同邻居，共同邻居数越多，两个节点的二阶相似度越高；Grover等人[11]通过最大限度地增加随机游走（DeepWalk）中后续节点发生的概率，产生了更优质的节点嵌入。（3）基于深度学习方法。Kipf等人[12]提出通过在图上定义卷积运算符解决图的稀疏问题，该方法迭代地聚集节点的邻居，并和之前迭代中获得的嵌入共同来获得新的嵌入；Wang等人[13]提出使用深度自动编码器保存网络的第一阶和第二阶相似性，通过共同优化这两个距离实现这一目标，该方法使用高度非线性的函数获得节点表示；Guo等人[14]将三头注意力与时序卷积网络结合，探索出一种基于时间卷积网络的特征学习方法，以获得节点表示；Ribeiro等人[15]忽略节点和边缘属性以及它们在网络中的位置来评估节点之间的结构相似性，然后建立层次结构来度量节点在不同尺度上的结构相似性，为节点生成随机上下文。

1.2 图摘要

图摘要用于解决大规模网络数据存储和计算方面的问题，当前图摘要工作主要分为三类：（1）基于分组和聚合的方法，通过应用现有的聚类算法将节点[16]或边[17]分组为超节点或超边的集合。Zhu等人[18]根据节点的标签和结构相似性将节点聚合成超节点来处理每个实体。（2）基于简化与稀疏的方法，Li 等人[19]提出了一种四步无监督算法，该算法使用边过滤来进行异构社交网络的自我中心信息抽象。（3）基于压缩的方法，Shah等人[20]通过最小化存储输入图所需的存储空间获取摘要。Jin等人[21]利用一组关系运算符和关系函数（运算符的组合）分别捕获网络结构和高阶子图结构，通过奇异值分解获得潜在摘要表示。另外，在文本摘要领域，周才东等人[22]通过局部注意力机制与卷积神经网络结合的方式提取文本的高层次特征，将其作为编码器输入，通过基于全局注意力机制的解码器生成摘要；田珂珂等人[23]结合基于自注意力机制的Transformer 模型，提出一种基于编码器共享和门控网络的文本摘要方法。

网络摘要和网络表示是互补的学习任务，具有不同的目标和输出，潜在网络摘要的目标是将两者结合，如图1所示，学习独立于图大小的摘要表示，并获取节点表示。本文通过应用更丰富的特征和关系算子捕获高阶子图信息，加强了对图结构信息的提取。此外，针对异构网络，例如有向图、权重图、标签图等，提出了不同的解决策略，生成独立于输入图大小（节点和边）的潜在摘要，并且能够获取节点表示。

2 问题描述与相关定义

问题描述潜在网络摘要：给定包含|V|=N个节点和|E|=M条边的任意图，潜在网络摘要的目标是将图G映射到大小为K×C的低维摘要表示S中，其中K,C≪M,N，且与图的大小无关。输出的潜在网络摘要能够重构节点表示，同时获得的节点表示能够为下游任务如链接预测提供服务。

定义1异构网络通常被定义为图G=(V,E)，其中V是所有节点的集合，E是所有边的集合。在图上存在一个节点类型映射函数θ和边类型映射函数ξ，对于每一个节点v∈V都有θ(v)∈O，O是所有节点类型的集合，同时，对于每一条边e∈E都有ξ(e)∈R，R是所有边类型的集合。如果在信息网络中，每个节点都有特定的节点类型，或者每条边都有特定的边类型，即|O|＞1或|R|＞1，那么这个网络为异构网络。

定义2（t类型邻居Nt）给定图G=(V,E)中任意一个节点i，节点i的t类型的邻居节点集合，即从i出发沿边e∈E一跳距离内的类型为t的节点集合。特别地，Ni表示节点i的所有邻居节点集合。

定义3（关系算子φ）关系算子φ(x,R)∈Φ为对特征向量x进行运算并返回单个值的基本函数，x与一组相关元素R相关联。例如，x为N×1的向量，R是节点i的邻居节点集合Ni，φ表示和算子，φ(x,R)将返回从节点i可到达的邻居的计数（节点i的未加权出度）。

定义4（关系函数fφ）关系函数是一系列关系算子φ的组合，即fφ=(φ1∘φ2∘…∘φh)，表示将不同关系算子应用到与R相关联的特征向量x进行运算返回的向量。fφ为h阶关系函数。

3 FELS模型

图摘要主要用于解决大规模网络数据存储和计算方面的问题，本文图摘要工作基于特征加强的异构网络潜在摘要模型FELS，如图2，主要包括三部分：首先，基于关系算子对选取的基本图特征进行特征加强，提取结构信息；其次，为了处理特征加强过程中可能导致的偏斜问题，针对不同属性的异构网络进行分类，根据不同的节点类型或边类型以及其他属性分别进行上下文提取，以获得优质的节点特征；最后，针对上下文特征矩阵使用奇异值分解获取潜在摘要，同时获得节点表示。

图2 特征加强的异构网络潜在摘要模型Fig.2 Feature-enhanced latent summarization model of heterogeneous network

3.1 基本特征选取与特征加强

异构网络包含上万甚至百万个节点，原图（节点集和边集）的邻接矩阵并不适合直接作为输入。本节通过基于节点属性从输入图中为每个节点生成一组基本图特征，作为原图的输入，然后应用特定关系算子组成的关系函数聚合节点高阶子图邻域间的结构特征，迭代生成一组包含自身节点和高阶子图结构特征的矩阵。

3.1.1 基础特征

基础特征根据不同的节点属性定义获得，本文将这种属性定义为B，属性可以指节点的邻接矩阵的行/列，或者与节点相关的其他导出向量，例如有向图，可以同时考虑节点的入/出/总出入度/加权度等。基础特征矩阵F(0)由多个向量fb构成，fb∈Fb由特征函数Ff获得，可以指选择的属性，然后将特征函数Ff应用到每一个节点，可以得到fb：

式中，b∈B，fb是N×1 的特征向量。例如，如果b表示出度的特征，那么fb＜b,N＞则表示图G中所有N个节点的出度特征向量，fb＜b,Ni＞表示Ni节点的出度。通过不同的节点属性信息B（出度、入度等），则可以得到N×|B|的基础特征矩阵F(0)：

式中，b1,2,…,|B|∈B。例如，节点间的边有向且带有权重，基础特征矩阵可取：

式中，bi、bo、bio分别表示入/出/总度，biw、bow、bw分别表示入/出/总边权重的特征。

基础特征矩阵F(0)聚集了原图N个节点的度特征以及所连边的权重特征，但是基础特征仅包含节点自身结构特征，计算过程类似于线性累加，不能学习邻域节点以及高阶邻域间的结构特征，因此加强对基础特征提取，进而获取邻域结构特征。

3.1.2 基于关系函数的特征加强

基础特征矩阵F(0)聚集了原图N个节点的度特征以及所连边的权重特征，但是基础特征仅包含节点自身结构特征，计算过程类似于线性累加，不能学习邻域节点以及高阶邻域间的结构特征，因此进一步对基础特征加强，进而获取邻域结构特征。

为了自动导出复杂的非线性节点特征，选择应用不同的关系算子加强对基础特征F(0)的邻域结构学习。本文迭代地将关系算子φ∈Φ应用于基础特征F(0)，聚合生成基本节点属性间的线性和非线性结构特征矩阵F(l)，关系算子φ包含均值、方差、和、最大值、最小值、L1距离、L2距离。将关系算子按特定顺序组合成关系函数(φ1,φ2,…,φ|Φ|)，运用在节点的邻域网络上，捕获节点l跳邻域的高阶结构特征。例如，fo表示由节点方向的出度组成的特征向量，sum 关系算子捕获节点i的一阶邻域Ni的出度和；max 关系算子捕获节点i的一阶邻域Ni中的最大出度数，对所有节点应用max 算子形成新的特征向量max(fo,N)，其中每个值记录相应节点邻域内的最大出度数。

如图3 所示，以节点3 为例，左侧展示了节点的一阶邻域（蓝色虚线）与二阶邻域（粉色虚线）；右侧描述了节点通过关系算子max 传递邻域间最大度数的方式以及以迭代方式传递最大节点度的过程。迭代过程中每次max 只考虑一阶邻域间最大度数，将max 关系算子应用到上一层获得的max(fb,N)上可以聚集更远邻域间的结构特征。

图3 max关系算子Fig.3 max relational operator

定义关系算子的迭代层数为l∈{1,2,…,L}，可以发现迭代学习获得结构特征是呈指数增长的。迭代过程如下：

式中，φ为一种关系算子；F(l)为迭代聚合第l层的结构特征矩阵；∘为对F(l-1)进行关系算子φ操作；F(0)为基础特征矩阵。

本文使用了定义的所有关系算子，即对特征矩阵的每一列特征向量都使用了|Φ|个不同关系算子的聚合操作，应用关系算子的特定顺序记录了关系函数是如何生成的，然后将这组关系函数与模型层数存放在中。与F(0)记录了结构特征矩阵F(l)的生成过程。

对于l层结构特征矩阵F(l)，|F(l)|=|B|×|Φ|(l)，|F(l)|表示特征列数大小，|Φ|表示定义的关系算子个数，可以发现F(l)特征列数是随着|Φ|大小呈指数增长的。本文的实验设置关系算子个数|Φ|=7，特征迭代次数L=2，有向图设置基本特征个数|B|=3，有向权重图设置基本特征个数|B|=6。

3.2 基础特征

3.2.1 上下文提取

使用关系函数(φ1,φ2,…,φ|Φ|)递归地提取结构特征，获得多层结构特征矩阵F(l)。如果直接作为节点表示导出，并不能达到很好的预期效果，这是由于无差别结构保留导致的特征偏斜。本小节通过考虑不同图属性隐藏的丰富的上下文信息，处理无差别结构提取造成的特征偏斜问题，最终生成异构网络的上下文矩阵。

图4 特征抽取Fig.4 Feature extraction

为了防止特征矩阵F(l)被映射过长导致过度膨胀，选择将节点特征向量f映射到大小的桶中，称为桶映射，t为设置的缩放比例，桶映射方式为：的第一列值等于的邻居节点数，f(i)表示节点i对应特征向量的值。使用这种映射方式有两个好处：（1）将特征向量f缩短到一个可管理的维度之内；（2）使获得的上下文表示对小的噪声更具鲁棒性，特别是对于高度较大的数据，使得小范围的值被映射到桶中的一个值中。

上下文特征提取的形式化过程如下：对于节点i,其第l层特征F(L)(i)是|F(l)|=|B|×|Φ|(l)维行向量，形式如下：

对于第l层结构特征矩阵F(L)：

式中，N为图G的节点数。

考虑结构统一性，以无向无属性图为例，将F(L)看作行向量：

ci形式如下：

式中，c1i为节点1 对应i列值。ci为第i列特征向量f，对应图3中的度特征，通过桶映射的方法，第一个节点c1i被映射到dk1 向量上，大小为1×logtD，对每个节点进行桶映射，ci被映射成N×logtD大小的矩阵，对每列特征向量f=c进行桶映射，结构特征矩阵f(L)=C被桶映射为上下文矩阵P，维度大小为N×(logtD×Z)。

3.2.2 针对其他属性图的策略

针对其他属性的网络图G，节点和边往往具有多种类型，处理多类型节点和边的思想是单独考虑每一个类型，将节点和边按照不同的类型进行分区处理，即将节点邻居按不同的类型分配到不同的桶中。针对不同属性图的处理如下：

3.3 异构网络潜在摘要

对异构网络学习得到的上下文矩阵一般较大，并且上下文矩阵可能存在重复结构，利用奇异值分解对上下文矩阵进行特征选择以获得潜在摘要与节点表示。

给定节点特征与图属性学习到的上下文矩阵C，通过矩阵的奇异值分解获得潜在摘要的表示，分解为C=Y·SC，其中SC为摘要表示，Y为节点表示。

具体的摘要过程如下：

式中，U为左特征向量矩阵；Σ为特征值矩阵；V为右特征向量矩阵，·表示矩阵乘法。

节点表示Y如下：

摘要表示SC如下：

通过摘要表示获得节点表示的过程：

其中摘要表示SC、关系函数(φ1,φ2,…,φ|Φ|)和基础特征矩阵F(0)组成了原潜在摘要S={F(0),(φ1,φ2,…,φ|Φ|),SC}，S保留了原图的结构信息，能够动态导出保持节点相似性的节点表示Y，潜在摘要S主体部分摘要表示SC与原图大小无关，实现了对大规模异构网络数据的压缩。

算法1 中提供了FELS 模型训练过程的伪码，具体如下。

算法1FELS

输入：属性图G，关系算子集Φ，节点嵌入维度K，上下文桶个数b。

输出：潜在摘要表示S。

4 实验与结果

4.1 实验设置

4.1.1 数据集

本文使用6个真实世界的异构网络数据集Hhar3、Hhar10、Reut3、Reut10、Movie、American，数据集地址http://networkrepository.com。其中Hhar3 和Hhar10属于不同边集规模的同一类数据集，Reut3 和Reut10属于不同边集规模的同一类数据集。数据集中包括标签图、权重图、有向图，详细数据统计如表1所示。

表1 数据集Table 1 Dataset

4.1.2 对比方法

使用FELS模型获得的节点表示进行链路预测，对比的基线方法中，基于矩阵分解方法有GF[6]、HOPE[8]、LP[5]、LLE[4]；基于随机游走方法有Dwalk[9]、S2vec[15]、N2vec[11]；基于深度学习方法有SDNE[13]；其他方法LINE[10]；MLS[21]与本文的FELS属于潜在摘要方法。

为了保证实验的公平性，本文中的所有方法均使用128 维度大小的embedding 进行链接预测实验，并且进行了5次实验取平均值作为结果展示。

4.2 链路预测

为了测试不同方法在链路预测任务上的性能，对于每个数据集，随机隐藏10%的网络边，使用剩余90%的边作为训练数据学习节点表示，对可能存在的边进行预测。与基线方法相比，FELS 模型的实验结果在各个数据集上均取得了最佳效果，AUC 与ACC比现有最好方法MLS 平均提高4 个百分点，具体实验结果如表2所示。

表2 潜在摘要生成节点嵌入与基线方法生成嵌入应用于链接预测任务的结果对比Table 2 Comparison of results of latent summarization generation node embedding and baseline method generation embedding applied to link prediction tasks 单位：%

4.3 变体实验

FELS 具有控制摘要与表示的能力，可以在精度和存储方面进行选择，即摘要体积越大，保留的图信息越多，表示原图能力就越强。本节设置了以下变体实验：

FELS-128：本文默认模型，节点表示维度为128，算子迭代层数为3。

FELS-64：将节点表示维度设置为64。

FELS-256：将节点表示维度设置为256。

FELS-C：将关系算子迭代过程中获得的特征进行拼接，节点表示维度设置为128。

FELS-L：关系算子迭代层数为2。

MLS：现有最好基线模型。

变体实验1 如图5 所示，在不同的数据集上，FELS-256模型的AUC分数都是最高的，同时图中节点表示维度越大，链路预测的AUC 分数越高，证明FELS模型可以通过设置维度大小在精度和存储空间上进行选择。

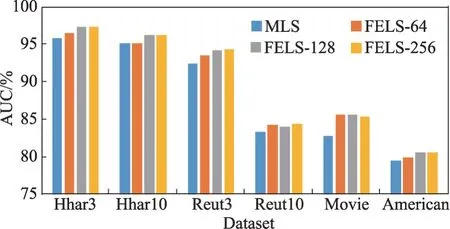
图5 变体实验1Fig.5 Variation experiment 1

变体实验2 如图6 所示，与本文默认模型FELS-128相比，在不同的数据集上，FELS-C模型的数据结果相差不大，说明在关系算子迭代过程中，较前层特征信息包含在后层较大特征表示中；而FELS-L模型的实验效果较差，说明在关系算子迭代过程中，较前层特征包含信息较少，后层特征信息更丰富。

图6 变体实验2Fig.6 Variation experiment 2

4.4 摘要存储

存储空间是度量摘要的一个关键指标，为了说明FELS方法在存储空间方面的优越性，选择大规模异构网络数据集进行实验，数据集包括Yahoo、Digg、Dbpedia、Bibsonomy，数据集地址http://networkrepository.com。详细数据与实验结果如表3所示。

表3 存储空间对比Table 3 Comparison of storage space

从实验结果可以看出，相较于节点表示存储，FELS方法获得的摘要表示仅占用其2%～10%的存储空间，同时节点表示EMB 随着图的大小（节点集）的增大而增大，摘要表示FELS 大小与图的大小无关，只与图的复杂度（边类型、图类型）有关。

4.5 迭代层数L

本节对不同迭代层数的FELS模型进行了比较，从实验结果表4可以看出，不同数据集对层数的训练要求不同。例如，针对边集数据较大的Movie 和Reut10 数据集，数据层数越大，AUC 分数越低；针对类型较多的Hhar 数据集，学习效果随迭代层数增大而增大，增长速率降低。综上，不同的数据集对迭代层数的受影响程度不同，不同的迭代层数表示对数据不同的学习程度，层数越深表示对数据学习得越充分，但是当层数达到一定深度的时候，可能会出现学习过于充分的问题。

表4 FELS-L链路预测对比Table 4 Comparison of link prediction of FELS-L

5 结束语

基于不同特征以及特征加强的方式，本文提出了基于特征加强的异质网络潜在摘要模型FELS，利用融合节点特征和图属性获得大规模异构网络数据的摘要表示，即首先通过输入图的边集，考虑原图中不同的节点特征信息作为基础特征，应用多种关系算子捕获高阶子图结构信息；然后，根据不同的图属性通过一种特殊映射方式学习上下文的潜在子空间结构信息；最后，由矩阵分解并进行特征选择从而获得潜在摘要表示。潜在摘要独立于输入图的大小，仅取决于网络的复杂性与异构性，并且能够捕获网络中关键的结构信息。与以往的方法相比，本文提出的FELS模型生成的节点表示在链路预测任务中，实验效果中AUC分数与现有最好模型MLS相比，在不同大小的数据集上均有4 个百分点的提升；同时，FELS 模型更简洁高效，潜在摘要仅占用原有节点嵌入的2%～10%的存储空间。在未来，将研究如何利用全局结构信息促进对图结构的提取，以获取更优质的摘要与节点表示。