可公开验证无对运算的无证书聚合签密方案

陈 虹，周 沫+，侯宇婷，赵菊芳，肖成龙，郭鹏飞

1.辽宁工程技术大学 软件学院，辽宁 葫芦岛125105

2.汕头大学 计算机系，广东 汕头515063

签密是在同一个操作步骤内实现公钥加密和数字签名两种功能，并保证消息的机密性和认证性。与签名和加密先后在两个步骤内完成的方式相比，签密的运算代价和通信开销大幅度降低，且安全系数和效率更高。1997年，Zheng[1]提出了签密的思想，并给出了具体的方案设计，满足消息的机密性和不可否认性。2002 年，Baek 等[2]提出了安全模型，用于验证签密方案是否满足自适应选择密文攻击下的语义安全性和自适应选择消息攻击下的不可伪造性。同年，Malone-Lee[3]将签密技术应用到基于身份的密码体制中设计了一个签密方案，但该方案的语义安全性后来被证明是不满足的。2005年，Chen等[4]也提出了一个基于身份密码体制的签密方案，并在双线性Diffie-Hellman假设下证明了其安全性。将签密技术与实际应用环境相联系，研究人员提出了不同种类的签密方案[5-10]。当签密用户较多，签密数量较大，接收者需要同时验证多个密文时，普通的签密方案不能达到理想的运算效率。聚合签密能够将多个签密消息合并为一个，减少密文验证的时间，非常适用于车载自组织网络、智能电网等计算资源和带宽受限的环境。2009年，Selvi等[11]结合聚合签名的思想设计了一个基于身份密码体制的聚合签密方案，提高了密文的批验证效率。2020年，Abouelkheir等[12]也提出了一个基于身份的聚合签密方案，并在椭圆曲线离散对数问题的假设下证明了安全性。但在上述方案中，用户私钥由私钥生成中心（private key generator，PKG）设置，存在着安全隐患，在实际应用中显露弊端。

2003 年，Al-Riyami 等[13]提出了更为安全的无证书密码体制，取消了公钥证书，解决了证书管理的过程复杂、代价高等问题，同时也克服了密钥托管问题，用户私钥不再由PKG统一设置，而是由密钥生成中心（key generation center，KGC）和用户合作生成。2011 年，Lu 等[14]提出了一个无证书聚合签密（certificateless aggregate signcryption，CLASC）方案，将聚合的思想应用到无证书签密中，凸显其优势。就此CLASC 成为研究热点，如何在保证方案安全性与可行性的同时，减小运算代价成为设计难题。之后，国内外学者提出了大量的CLASC方案，如Eslami等[15]、张玉磊等[16]和刘建华等[17]提出的CLASC方案。上述方案在签密及验证阶段需要进行大量的双线性对运算和指数运算，这两种运算与点乘运算相比，代价极高。苏靖枫等[18]和李晨等[19]提出的CLASC 方案，虽没有使用效率较低的双线性对运算，但在解签密阶段需要4n次点乘运算，以及胡荣磊等[20]提出的物联网环境下的CLASC 方案，在解签密阶段需要5n+1次点乘运算，运算效率仍有待提升。将聚合签密的优点应用于异构网络中，牛淑芬等[21]和刘祥震等[22]提出了异构聚合签密方案，实现了异构密码环境中的“多对一”传输，但在签密验证阶段使用了双线性对运算，效率较低。

传统公钥密码体制下的签密需要证书机构（certificate authority，CA）颁发公钥证书，证书管理的成本较高，不适合大规模应用；基于身份的签密将用户的公钥与身份解绑，消除了公钥证书，但存在密钥托管问题，PKG 持有所有用户的私钥；无证书签密既无CA 也无密钥托管问题，更安全更高效，现阶段对签密的研究主要基于无证书的密码体制。签密的传输模式也从最开始“一对一”的传输逐渐发展为“多对一”的聚合传输，聚合签密可聚合传输且能批量验证，大大降低了通信开销。大多数的聚合签密方案都使用了双线性对运算，安全性得到了保证但运算速度较慢。基于椭圆曲线离散对数的聚合签密方案虽不含双线性对，效率较高，但安全程度略有降低。

为了提高无证书聚合签密的运算效率，本文基于Qu 等[23]提出的安全性强且效率较高的签名方案，构造了一个新的可公开验证无对运算的CLASC 方案。主要工作可分为以下三方面。

（1）构造了一个可公开验证无对运算的CLASC方案，该方案基于无证书密码体制，避免了使用代价较高的CA，且无密钥托管问题。未使用双线性对运算和指数运算，仅使用点乘运算。

（2）对本文方案进行了完整的安全性证明，结果表明，该方案在随机预言模型下满足安全性，并具有公开验证性。

（3）从理论分析方面对本文方案进行了评估，将该方案与六个相关的聚合签密方案进行了比较，结果表明，该方案在解签密阶段只需要3n次点乘运算，运算效率较高。并对该方案进行了仿真实验，实验结果表明，聚合签密极大地提高了密文的验证效率。

1 预备知识

1.1 困难性问题

（1）计算性Diffie-Hellman（computational Diffie-Hellman，CDH）问题：已知G是椭圆曲线上的加法循环群，G的阶为大素数q，生成元为P，CDH问题是指给定元组(P,aP,bP)，其中a,b∈未知，求解abP的值。

（2）离散对数（discrete logarithm，DL）问题：已知G是椭圆曲线上的加法循环群，G的阶为大素数q，生成元为P，DL 问题是指给定元组(P,aP)，其中a∈未知，求解a的值。

1.2 无证书聚合签密方案定义

CLASC 方案的参与方有三个，分别为KGC、签密者IDi(1 ≤i≤n)和接收者IDB。具体算法如下：

（1）系统参数生成：输入安全参数k，KGC 输出系统主密钥x和参数params，保密x，公开params。

（5）聚合签密：输入n个签密密文σi，聚合签密者计算并输出聚合签密密文σ。

1.3 无证书聚合签密方案的安全模型

CLASC 方案的安全模型存在两类敌手[13]：一类模拟恶意的用户，可以将用户原有的公钥进行替换，但不能得知系统主密钥；另一类模拟恶意的KGC，可以得知系统主密钥，但不能进行替换用户公钥的操作。因此，CLASC 方案的安全性需考虑在两类敌手攻击下的保密性和不可伪造性。以敌手A1为例，敌手与挑战者C之间的交互如图1、图2所示。

图1 适应性选择密文攻击的示意图（敌手A1）Fig.1 Schematic diagram of adaptive chosen ciphertext attack(adversary A1)

图2 适应性选择消息攻击的示意图（敌手A1）Fig.2 Schematic diagram of adaptive selection message attack(adversary A1)

定义1（敌手A1攻击下的保密性）如果不存在任何多项式数量级的敌手A1能够在下面的游戏中以不可忽略的优势获胜，那么称该方案具有适应性选择密文攻击下不可区分的安全属性（indistinguishability under adaptive chosen ciphertext attack，IND-CCA2）。

系统参数生成：输入安全参数k，挑战者C运行系统参数生成算法，生成系统参数params和系统主密钥，并将params发送给敌手A1。

第一阶段问询：敌手A1可适应性地进行以下多项式数量级的问询：

（1）部分私钥问询：A1输入用户身份IDi进行问询，C返回IDi的部分私钥。

（2）公钥问询：A1输入用户身份IDi进行问询，C返回IDi的公钥。

（3）秘密值问询：A1输入用户身份IDi进行问询，C返回IDi的秘密值。

（4）公钥替换问询：A1输入用户身份IDi和新公钥进行问询，C将IDi现有公钥进行替换并记录。

（5）签密问询：A1输入消息mi、签密者身份IDi和接收者身份IDB进行问询，C返回密文σi。

（6）聚合签密问询：A1输入消息mi、签密者身份IDi和接收者身份IDB进行问询，C返回聚合密文σ。

（7）解签密问询：A1输入签密σi和接收者身份IDB进行问询，C返回消息mi。

挑战：经过足够的问询后，A1选择两个长度相等的明文mi(i∈{0,1})和用户身份IDi、IDB。C判断IDB是否为挑战对象，若不是则拒绝；否则，C随机选择一个比特b，对明文消息mb进行签密得到密文σ*，返回给A1。

第二阶段问询：与第一阶段问询类似，不同之处在于不能进行IDB的部分私钥问询和σ*的解签密问询。

猜测阶段：A1给出一个猜测值b′，若b′=b，则敌手A1取得游戏胜利。

定义2（敌手A2攻击下的保密性）如果不存在任何多项式数量级的敌手A2能够在下面的游戏中以不可忽略的优势获胜，那么称该方案具有适应性选择密文攻击下不可区分的安全属性（IND-CCA2）。

系统参数生成：输入安全参数k，挑战者C运行系统参数生成算法，将生成的系统参数params和主密钥都发送给敌手A2。

第一阶段问询与定义1类似，不同之处在于不能进行公钥替换问询和部分私钥问询。

第二阶段问询与定义1类似，不同之处在于不能进行IDB的秘密值问询。

挑战阶段和猜测阶段与定义1相同。最终，敌手A2取得游戏胜利。

定义3（敌手A1攻击下的不可伪造性）如果不存在任何多项式数量级的敌手A1能在下面的游戏中以不可忽略的优势获胜，那么称该方案具有适应性选择消息攻击下不可伪造的安全属性（existential unforgeability under adaptive chosen messages attack，EUF-CMA）。

系统参数生成和问询阶段与定义1相同。

定义4（敌手A2攻击下的不可伪造性）如果不存在任何多项式数量级的敌手A2能够在下面的游戏中以不可忽略的优势获胜，那么称该方案具有适应性选择消息攻击下不可伪造的安全属性(EUF-CMA)。

系统参数生成和问询阶段与定义2 相同。伪造阶段与定义3相同。最终，敌手A2取得游戏胜利。

2 本文无证书聚合签密方案

本文构造的CLASC 方案包括系统参数生成、部分密钥设置、用户密钥设置、签密、聚合签密、解签密和聚合解签密七个部分。以签密过程为例，本文CLASC方案如图3所示。

图3 本文CLASC方案Fig.3 CLASC scheme of this paper

方案具体如下：

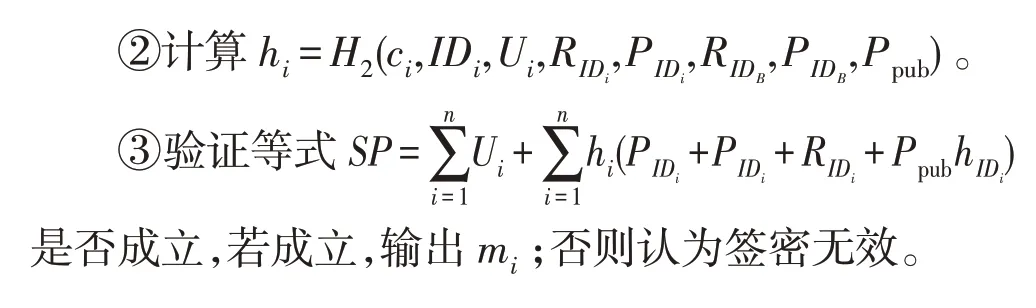
3 本文方案安全性分析

3.1 正确性

（1）密钥的正确性

用户IDi通过以下等式验证部分密钥是否有效：

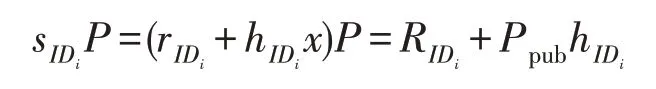
（2）消息的正确性

接收者IDB通过以下等式验证消息mi的正确性：

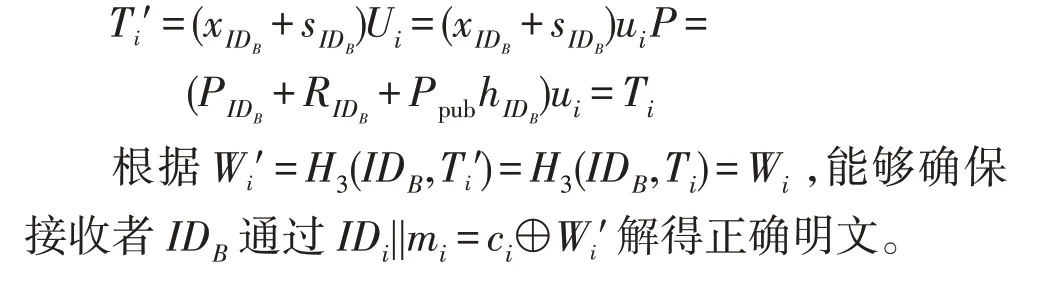
（3）签名的正确性

接收者IDB通过以下等式验证签名的正确性：

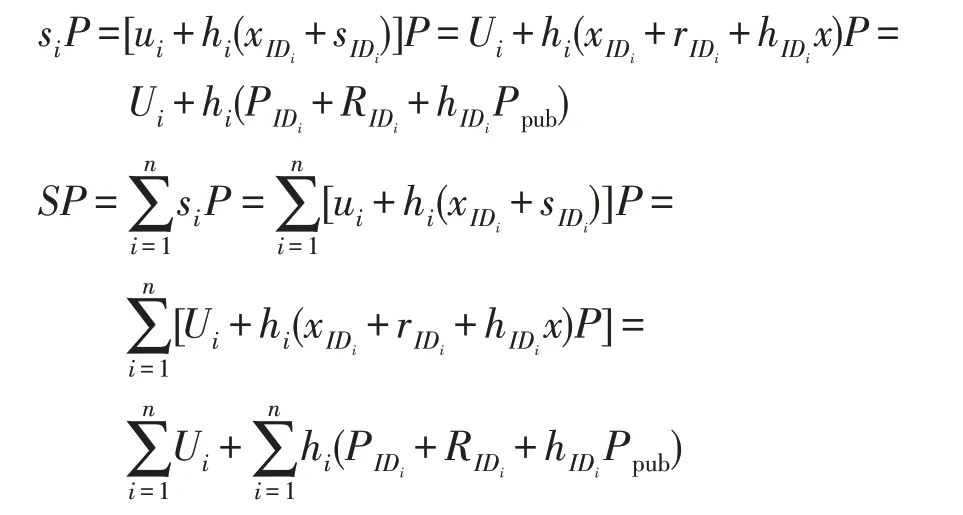
若等式成立，则发送者身份验证成功，消息mi能够被接收。

3.2 公开验证性

3.3 机密性

若存在敌手A1、A2具有不可忽略的获胜优势的情况，则A1、A2具有帮助挑战者C破解困难问题的能力。

引理1（敌手A1攻击下的保密性）在随机预言模型中且CDH 问题难解的情况下，根据定义1 知敌手A1攻击成功的优势是可忽略的。如果在概率多项式时间内，A1能够以不可忽略的优势ε（最多经过qi（i=1,2,3）次Hi问询、qpsk次部分私钥问询、qs次签密问询、qun次解签密问询等）赢得游戏IND-CLSCCCA2，那么就存在挑战者C在概率多项式时间内以概率的优势解决CDH困难问题。

证明如果A1能够以不可忽略的优势赢得游戏IND-CLSC-CCA2，则C能够在A1的帮助下成功解决CDH 问题。其中，C在游戏中的角色为挑战者，A1为C的子程序。即已知{P,aP,bP}，求abP的值。

（1）系统参数生成：C运行系统参数生成算法，设置Ppub=aP，将参数params发送给敌手A1。

（2）问询阶段：A1进行以下问询，并将问询的值记录在各列表中，所有列表初始化为空。

A1收到σ*后继续问询，与问询阶段类似，不同之处在于不能进行IDB的部分私钥问询和σ*的解签密问询。经足够的问询后，A1输出对b的猜测b′，若b′=b，则C输出作为CDH问题的解，其中，

若A1进行过IDB的部分私钥问询，进行过H2问询，进行过的H3问询，则游戏失败。A1未进行过部分私钥问询的概率至少为1/q1，未进行过H2问询的概率至少为1/q2，未进行过的H3问询的概率至少为1/q3，且挑战者C未拒绝有效签密的概率至少为，则C成功解决CDH问题的概率为因为A1赢得游戏的优势是可忽略的，所以C成功解决CDH 困难问题的前提条件不存在。根据定义1所述，本文方案具有保密性。证毕。

引理2（敌手A2攻击下的保密性）在随机预言模型中且CDH 问题难解的情况下，根据定义2 知敌手A2攻击成功的优势是可忽略的。如果在概率多项式时间内，A2能够以不可忽略的优势ε（最多经过qi（i=1,2,3）次Hi问询、qpsk次秘密值问询、qs次签密问询、qun次解签密问询等）赢得游戏IND-CLSCCCA2，那么就存在挑战者C在概率多项式时间内以概率的优势解决CDH困难问题。

证明如果A2能够以不可忽略的优势赢得游戏IND-CLSC-CCA2，则C能够在A2的帮助下成功解决CDH 问题。其中，C在游戏中的角色为挑战者，A1为C的子程序。即已知{P,aP,bP}，求abP的值。

（1）系统参数生成：C运行系统参数生成算法，设置Ppub=xP，将参数params和x发送给敌手A2。

（2）问询阶段：A2进行以下问询，并将问询的值记录在各列表中，所有列表初始化为空。

3.4 不可伪造性

引理3（敌手A1攻击下的不可伪造性）在随机预言模型中且DL 问题难解的情况下，根据定义3 知敌手A1攻击成功的优势是可忽略的。如果在概率多项式时间内，A1能够以不可忽略的优势ε（最多经过qi（i=1,2,3）次Hi问询、qpsk次部分私钥问询、qs次签密问询、qun次解签密问询等）赢得游戏EUF-CMA，那么就存在挑战者C在概率多项式时间内以概率的优势解决DL困难问题。

证明如果A1能够以不可忽略的优势赢得游戏EUF-CMA，则C能够在A1的帮助下成功解决DL 问题。其中，C在游戏中的角色为挑战者，A1为C的子程序。即已知{P,aP}，求a的值。

初始化阶段与问询阶段同引理1。

引理4（敌手A2攻击下的不可伪造性）在随机预言模型中且DL 问题难解的情况下，根据定义4 知敌手A2攻击成功的优势是可忽略的。如果在概率多项式时间内，A2能够以不可忽略的优势ε（最多经过qi（i=1,2,3）次Hi问询、qpsk次秘密值问询、qs次签密问询、qun次解签密问询等）赢得游戏EUF-CMA，那么就存在挑战者C在概率多项式时间内以概率的优势解决DL困难问题。

证明如果A2能够以不可忽略的优势赢得游戏EUF-CMA，则C能够在A2的帮助下成功解决DL 问题。其中，C在游戏中的角色为挑战者，A2为C的子程序。即已知{P,aP}，求a的值。

初始化阶段与问询阶段同引理2。

因此，C成功解决了DL 问题。A2未进行过秘密值问询的概率至少为，A2伪造的签密为一个有效的聚合签密且z1=0，zi=1(2 ≤i≤n)的概率至少为εδ(1-δ)n-1，则C成功解决DL 问题的概率为因为A2赢得游戏的优势是可忽略的，所以C成功解决DL困难问题的前提条件不存在。根据定义4 所述，本文方案具有不可伪造性。证毕。

4 本文方案性能效率分析

4.1 理论分析

将本文方案与聚合签密方案文献[12，18-21，24]的运算效率和安全性进行比较，假设参与签密的用户共有n个，e 表示指数运算，s 表示群G上的点乘运算，p 表示双线性对运算。相比较以上三种运算，哈希运算、异或运算和加法运算的耗时对整体效率的影响可以忽略不计。方案分析结果如表1所示。

从表1可以看出，当消息个数为1个时，文献[21，24]的运算总量分别为e+4p+2s 和e+3p+5s，都使用了指数运算、双线性对运算和点乘运算。根据Cao等[25]的实验表明，一次双线性对运算所需要的计算代价约为一次点乘运算的20 倍，一次指数运算所需要的计算代价约为一次点乘运算的3 倍。就计算代价而言，本文方案的计算代价远远小于以上两种方案。文献[12，18-20]和本文方案一样只使用了点乘运算，其中文献[19-20]在各个阶段的运算量都比本文方案大，而文献[12，18]虽然在签密阶段的运算量和本文方案相同，但在解签密阶段的运算量分别比本文方案多出一次和两次点乘运算，运算代价仍比本文方案高。

表1 签密方案运算效率与安全性比较Table 1 Comparison of efficiency and security of signcryption schemes

当消息个数为n个时，本文方案的计算代价依旧远远小于使用了复杂运算的文献[21，24]。文献[12，19]的运算总量分别比本文方案多出2n-1 和2n+2次点乘运算，无论是签密阶段还是解签密阶段，本文方案的运算效率都更高。文献[18，20]虽然在签密阶段的运算量和本文方案相同，但在解签密阶段的运算量分别比本文方案多出n和2n+1 次点乘运算，运算代价仍比本文方案高。文献[21]在聚合签密验证阶段，需要使用Rsj的值，即根据接收者的私钥计算，任意第三方无法计算该值；文献[24]在聚合签密验证阶段，需要使用ri的值，即根据接收者的私钥计算，任意第三方也无法计算该值；文献[12]在签密的验证阶段虽然不需使用用户的私钥，但需使用明文消息，如果进行公开验证会泄露明文消息，因此上述方案均不满足公开验证性。综上，本文方案具有明显优势。

4.2 仿真实验分析

实验环境：Intel Core i5-5200U@2.20 GHz CPU，4 GB RAM，Windows 10操作系统，python 3.6.8。

实验结果分析：用户身份IDi唯一，明文消息|m|长度随机，消息个数n分别取1、5、10、20、50、100、200，实验结果包括n个消息的签密时间和解签密时间，如图4、图5所示。

图4 签密效率Fig.4 Signcryption efficiency

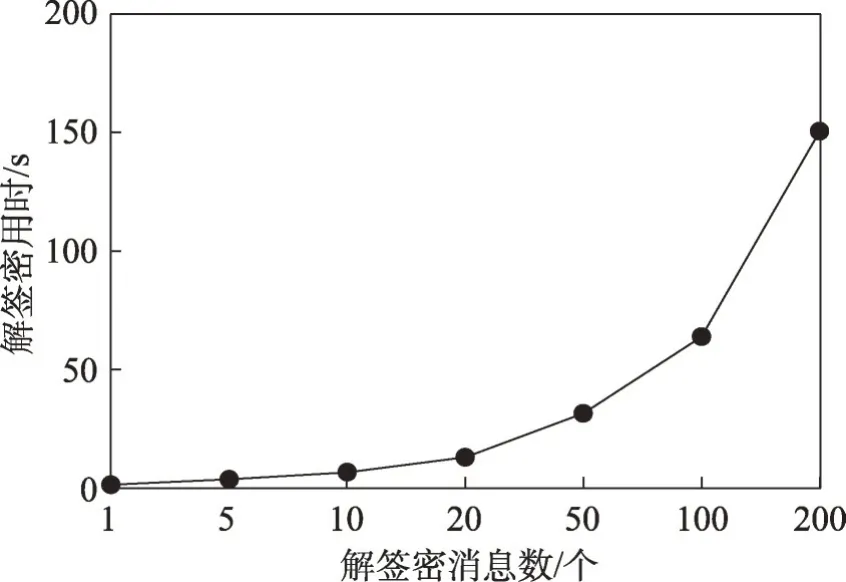
图5 解签密效率Fig.5 Efficiency of de-signcryption

解签密用时分别为1.390s、3.655 s、6.655 s、12.999 s、31.533 s、63.823 s、150.559 s，实验结果表明聚合密文解签密的时间约为n个密文分别解签密时间的1/2，极大提高了密文的验证效率。

5 案例设计

本文方案可以应用在智能交通系统中，车载自组织网络（vehicular ad hoc network，VANET）是智能交通系统的基础。VANET是一种将网络节点建立在汽车和道路基础设施上的分布式、动态变化的无线自组织通信网络。VANET 结构包括服务中心、车载单元（on board unit，OBU）和路边单元（road side unit，RSU）三部分。服务中心为信任机构，拥有最高的管理权限，负责OBU和RSU的登记管理。OBU安装在每辆车上，RSU安装在道路两侧或十字路口，OBU与OBU、OBU与RSU之间通过无线信道进行通信，构成一个无线自组织通信网络。VANET结构如图6所示。

图6 VANET结构Fig.6 VANET structure

由于VANET 节点多、规模大，且无线网络本身的脆弱性和开放性，VANET 很容易受到攻击，如窃听、篡改、跟踪和用户隐私泄露等，信息安全问题严重阻碍其发展。签密技术能够较好满足VANET 中信息传输的保密性、认证性等安全需求。

智能化交通系统中，1个RSU通常需要管辖上百辆车辆，要求RSU在短时间内验证大量签密消息，对RSU 的硬件和成本挑战过高，需要一种快速高效的验证技术用于大批量密文验证。本文提出的CLASC方案是能够进行压缩和批处理的聚合签密方案，可应用于OBU 与RSU 之间通信。方案中的n个签密者为VANET 中的n个OBU，接收者为RSU，n个OBU 产生n个签密消息并进行聚合，将聚合签密消息发送给RSU，由RSU进行验证并解签密，能够有效降低计算与通信开销，确保消息传递的安全性及有效防止伪造消息。

6 结束语

本文基于Qu 等[23]提出的签名方案，构造了一个可公开验证无对运算的CLASC 方案，与运算时间约为点乘20倍的双线性对运算相比，效率更高。同时，在随机预言模型下，该方案被证明满足安全性，并能够验证发送者的身份是否合法。对比其他6个方案，该方案性能更佳，可以很好地应用于计算资源和带宽受限但安全性需求较高的环境中。聚合签密提高了用户较多情况下的签密和解签密的效率，但如何在满足安全性的前提下，构造更为高效的聚合签密方案仍是日后研究的重点。