波弗特-楚科奇海夏秋季海浪极值波高特征分析❋

王艺智，李静凯，曾文华，管长龙

(1.中国海洋大学海洋与大气学院，山东 青岛 266100；2.中国海洋大学物理海洋教育部重点实验室，山东 青岛 266100；3.国防科技大学气象海洋学院，湖南 长沙 410015)

受全球气候变化的影响，在过去几十年里，北极海冰的覆盖面积与平均厚度均呈现出不断减小的趋势，其中在夏季表现的尤为显著[1]。1979—2019年北极9月份的海冰平均面积已减少50%[2]。在海冰覆盖面积减小的同时，冰层的厚度也在不断变薄，1987—2007年北极海冰平均厚度从3.7 m减少到2.6 m[3]，一些海区(如：北冰洋中部和东部)的多年冰逐渐变为了一年冰[4]。北极海冰减少最直接的影响之一便是开阔水域的增加，这就为海浪的成长提供了更长的风区，因此更加有利于海浪的成长。Wang等[5]通过对1970—2013年波弗特海、白令海和楚科奇海的海浪再分析数据的研究发现，7—9月海浪的平均有效波高每年增加3%～8%，平均周期每年增加3%～4%。目前，有效波高超过1 m已成为波弗特-楚科奇海秋季开阔水域典型的海浪特征[6]。对于70°N以北的一些海域，如巴伦支海、楚科奇海部分区域夏季极值波高的平均值也已可达3～4 m[7]。2015年“R/V Sikuliaq”号巡航期间，Thomson等[8]使用波浪浮标观测到波弗特海域一次大浪过程的有效波高高达到5 m。可以说，前所未有的北极海浪已经成为当前北极环境变化的显著特征之一。亦有相关预测表明，整个北冰洋到2050年后，夏季将不再结冰[9]。倘若这成为现实，也就意味着在未来一段时间内，由北极海冰覆盖范围继续减少所引起的海浪平均波高的增加将会更加显著[10]。

北极海域海冰的不断融化无疑为北极航道的通航提供了更加便利的自然条件[11]。2011年以来，已有二百多艘船只使用北极航线[12]开展了相应的经济活动。虽然开阔水域的增加为北极航道的通航提供了便捷，但与此同时逐年增强的海浪也对船只通航的安全性提出了挑战。在北冰洋诸多边缘海中，楚科奇海位于楚科奇半岛和阿拉斯加之间，波弗特海位于阿拉斯加北部和加拿大西北部沿岸以北至班克斯岛之间，北极群岛以西。对于中国而言，波弗特-楚科奇海是北极航道的必经之路，因此了解该海域的海浪变化特点，尤其是极值波高特征，对于保障中国船只的安全通航等海上活动是十分必要的。但受制于多种原因，以往的研究中对此却关注不够。

极值波高的特征研究以及典型重现期波高的推算，通常都要以该区域长时间的波高数据为依据。而针对波弗特-楚科奇海如此大范围的海域，考虑到现场观测数据时间上不连续，空间覆盖范围十分稀疏的特点，仅凭现场观测数据显然是远远不够的[10]。卫星高度计数据可以较好地弥补以上问题，但是受制于卫星轨道的制约，高度计采样依然存在着一定的稀疏性(欠采样)，导致很难保证捕捉到极端海况，并且也无法获得波向等其他有效信息。因此，为全面了解并分析波弗特-楚科奇海域海浪的极值波高特征，本文基于第三代海浪模式的多年数值追算结果开展了相应的分析研究。第三代海浪模式可以有效地量化海浪能量随波动频率及方向的变化，发展到今天，已具有稳定性好、计算精度高等特点[13]，因此是一种分析北极波候的有效手段[9，14]。

一年之中，北极海冰在夏季覆盖面积较小，通常在9月份达到极小值，从而对应的开阔水域面积最大，海浪更容易充分成长。初秋时分，新冰还未大量升成，但是海表面风速却有明显增强，海浪过程同样十分显著[6]。因此，本文选择针对波弗特-楚科奇海夏秋季每年9—10月的海浪进行21年(1996—2016年)的数值追算，利用数值模拟的数据分析了该海域的极值波高特征并开展了相关推算，旨在进一步认识波弗特-楚科奇海的海浪特征。

1 数据方法

本文采用了荷兰代尔夫特理工大学(Delft University of Technology)研制开发的第三代海浪数值模式SWAN(Simulating Waves Nearshore)[15]，该模式基于欧拉近似的波作用量平衡方程，采用线性随机表面重力波理论，可通过输入地形、流场、风场等数据来获取近岸、湖泊以及河口等海域的波浪参数[16]。其中，波作用量N是空间(x,y)、时间(t)、频率(σ)和传播方向(θ)的函数，本研究计算中所采用的控制方程由下两式给出：

(1)

Stot=(1-αice)(Sin+Sds,w)+Snl3+Snl4+Sds,b+Sds,br+αiceSice。

(2)

(1)式中：Stot为源/汇项，表示海浪产生、耗散或重新分配波浪能量的各物理过程，由(2)式给出。(2)式中：Sin为风输入项[17]；Snl3和Snl4分别表示三波相互作用[18]和四波相互作用[19]引起的波能非线性转移；Sds,w和Sds,b分别表示白冠耗散项[20]和底摩擦项[21]；Sds,br为深度诱导的破碎项[22]；Sice和αice分别为海冰耗散项和海冰密集度。

尽管同为第三代海浪模式，但相对于WAM[23]和WAVEWATCH Ⅲ[24]而言，SWAN是专门为浅水海浪模拟开发的数值模式，在源函数项的处理和数值计算上均有相应的考虑，已在近海海浪数值计算中得到了广泛的应用。同时，SWAN在41.31版本中加入了海冰源项，使用IC4M2参数化方案[25]来表示海冰对海浪能量的耗散，因此具备了计算海冰覆盖海域海浪的能力。同时，海冰强迫场的加入对于无冰区域的有效风区的长度也会产生影响，使得这些区域的海浪参数的计算更为符合实际[26]。针对波弗特-楚科奇海的环境特点，本文认为SWAN海浪模式适用于该海域的海浪数值模拟。一方面，波弗特-楚科奇海的岸线较长，近海海域(水深多不足500 m)面积较大，与SWAN模式的模拟优势比较契合。另一方面，波弗特-楚科奇海的海冰对海浪的影响可以在数值模拟中得以体现，例如在海冰边缘区(MIZ)，模拟结果相对于以往忽略海冰效应的海浪数据更为可靠。

1.1 SWAN参数配置

表1 SWAN设置中的源项方案使用情况Table 1 The source terms used in the SWAN model

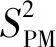
Sice/E=-2cgki，

(3)

ki(f)=c2f2+c4f4。

(4)

(3)式中：E为海浪能谱；cg为群速度；ki为波动振幅的衰减率，由(4)式确定。参考Rogers等[28],(4)式中与频率相关的多项式系数c2设为1.16×10-4s2/m；c4设为1.18×10-2s4/m。间接影响则是对风输入项Sin与白冠耗散项Sds,w的比例化，体现在(2)式中(1-αice)(Sin+Sds,w)两项，即Sin和Sds,w两项按无冰开阔水域的比例(1-αice)变化。模式中其他相关参数均采用默认设置。

1.2 水深地形网格

本文中SWAN模式所使用的网格为三角网格，相比传统矩形网格，其优势在于可以更好地贴合岸线，以提高近岸海浪要素计算的精度。本文所使用的三角网格覆盖范围为：140°E—80°W，65°N—85°N(示于图1左上子图中，网格范围大于图1中所示范围，以确保来自其他海域的涌浪对波弗特-楚科奇海海浪的影响得以体现)，网格平均水平空间分辨率约为8 km。水深数据(见图1)来源于etopo1全球地形数据，通过线性插值插值到各网格点上。

1.3 强迫场数据

本文数值模拟中所采用的风场数据为欧洲中期预报中心的海表面10 m风速的再分析数据ERA-interim(https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/)，空间分辨率为0.125(°)×0.125(°)，时间分辨率为6 h。数值模拟中所采用的冰场数据来源于德国汉堡大学的ASI-SSMI海冰密集度数据(https://icdc.cen.uni-hamburg.de/en/seaiceconcentration-asi-ssmi.html)，由SSM/I(Special Sensor Microwave / Imager)和SSM/IS(Special Sensor Microwave / Imager Sounder)传感器，通过ASI算法得到，空间分辨率为12.5 km×12.5 km，时间分辨率为24 h，使用球面投影网格储存，纬度覆盖范围由南北纬45°到两极。本文在使用该数据时，对其进行了相应的插值处理，通过线性插值插值到模式网格中。这两组强迫场数据在以往极地海浪的研究中也有着较为广泛的应用和较好的模拟效果[10,29]。

1.4 现场观测数据

为了确保数值模拟结果的准确性，本文选用来自现场的海浪观测数据对模拟的有效波高进行了验证。所使用的现场观测数据包括：2012年声学波浪剖面流速仪(AWAC,Acoustic Wave and Current)传感器数据[8]和2016年布放的两个WII(Waves In Ice buoys)漂流浮标数据[12]。AWAC传感器的位置为75°N、150°W，锚定在水下50 m处，锚定点水深3 000 m，如图1中黄点所示，观测时段为2012年8月13日—10月29日，时间分辨率为1 h，存在少量缺测值。两个WII浮标为漂流浮标，移动范围约在70°N—75°N，200°E—210°E之间，轨迹分别如图1中红色和绿色实线所示，观测时段为2016年9月10日—11月2日，时间分辨率为1 h，存在少量缺测值。

2 SWAN模拟结果与观测数据的对比

本文将2016年9、10月份两个WII浮标以及2012年9、10月份AWAC传感器记录的有效波高和SWAN模拟的有效波高绘制时间序列对比图(见图2)。为了充分体现当前模式的模拟能力及潜在的问题，图2中同样给出了ERA-Interim再分析有效波高的数据进行了对比。总体来看，SWAN模拟的有效波高变化与两个WII浮标的观测记录吻合良好，有效波高超过2 m的海浪过程SWAN模式基本能较好地还原，尤其是9月19日WII1和WII2浮标分别记录到的4.86和4.63 m极值波高，SWAN模式的重现结果比较令人满意。然而，有效波高的峰值在10月下旬被整体低估了，10月22日WII1和WII2浮标分别记录到的4.02和4.71 m极值波高，SWAN模式未能较好的重现，误差在1 m以上，初步分析，造成该误差的原因之一可能是由强迫风场的低分辨率造成的，它不能捕捉小范围内风场的剧烈的变化[30]。相比之下，ERA-Interim再分析有效波高数据与两个WII浮标记录的有效波高数据对比结果整体更好。从图2(a)与(b)中可看出，在10月7—17日期间，ERA-Interim再分析有效波高的回报结果明显好于SWAN模式的回报结果。但是，ERA-Interim再分析数据对于大波波高的回报结果也是存在着一定的偏差。

将SWAN模式结果与AWAC观测数据进行对比，结果显示，SWAN模式整体高估了2012年9、10月75°N、150°W区域的波高。虽然SWAN模式较为准确地回报了9月18日和10月15日左右的极值波高，但对于9月8日、10月10—23日左右的极值波高，SWAN模式并未能准确回报，高估了1 m以上。相比而言，ERA-Interim再分析数据更好的回报了AWAC传感器记录的有效波高，但却高估了10月10日的极值波高近1 m。

为了更好地量化分析模式误差，本文进一步计算了平均偏差、平均绝对误差、均方根误差和相关系数，结果示于表2。从整体的误差分析结果来看，SWAN模拟的有效波高数据准确性低于ERA-Interim再分析有效波高数据。然而，对于本文更侧重的大波的波高而言，结合图2的讨论，尚无法确定SWAN模式的结果与ERA-Interim再分析数据二者之中谁与实测数据的偏差更小，所以本文进一步对不同波高分段的两种数据的准确性作进一步的量化。

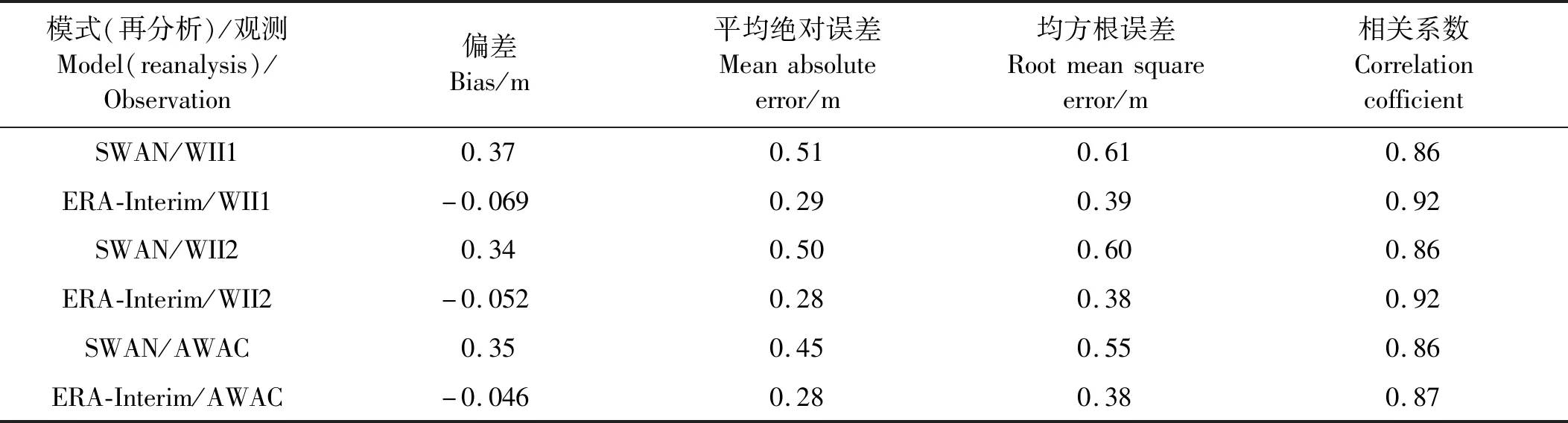
表2 SWAN模拟和ERA-Interim再分析有效波高与实测有效波高的误差统计Table 2 The statistics of errors between measured,modeled(SWAN) and ERA-Interim reanalysis significant wave height

将WII浮标与AWAC传感器记录的所有波高数据按区间分段，分别计算每个区间内SWAN模式数据和ERA-Interim再分析数据与观测数据之间的偏差、相对误差与均方根误差，并绘制直方图示于图3。在有效波高小于2 m的区间内，ERA-Interim再分析数据的偏差、相对误差与均方根误差均明显小于SWAN模式数据的对应值；在有效波高大于2 m小于3 m的区间内，SWAN模式数据的偏差与相对误差略小于ERA-Interim数据，但均方根误差略大；在有效波高大于3 m的区间内，SWAN模式数据的偏差与相对误差要明显小于ERA-Interim数据，而二者的均方根误差并无明显差别。可见，ERA-Interim再分析数据对于有效波高小于2 m的海浪过程的回报准确较高；而SWAN模式数据对于有效波高大于3 m的海浪过程回报结果更好；对于有效波高在2～3 m之间的海浪，二者回报结果的差距不大；但我们注意到，对于有效波高大于2 m的海浪，ERA-Interim再分析数据的偏差为负，说明其普遍低估了有效波高2 m以上海浪的有效波高。综上，由于本文侧重于极值波高与重现期波高分布规律的研究，故使用SWAN模拟的有效波高数据作为研究数据样本期待能得到更加准确的结果。

通过与WII和AWAC实测数据的对比，整体来看，ERA-Interim再分析数据的精度是高于SWAN模式结果的。考虑到观测位置均位于深海大洋内部，SWAN模式相对于基于WAM模式的再分析数据并无优势，加之ERA-Interim再分析数据还同化了大量的卫星高度计、浮标等观测数据，该结果亦是可以预见的。不过，本文的研究侧重于波弗特-楚科奇海极值波高的特征分析，而针对大浪波高的模拟，当前SWAN的模拟精度与ERA-Interim再分析数据相当，甚至略高。此外，SWAN模式相较于ERA-Interim能提供更加丰富的数据(如：ERA-Interim再分析波向数据在高纬度存在大量的缺失)，且在近岸预期有更高的精度，故本文将继续采用基于SWAN模式的多年追算结果进一步分析波弗特-楚科奇海的极值波高特征。

3 各级浪高频率分布

利用SWAN数值追算得到21年(1987—2007年)9、10月的有效波高数据(时间间隔为6 h)，本文分别统计了在此期间整个波弗特-楚科奇海有效波高大于1，2和3 m的各级浪高出现的次数，进而得到各级浪高出现频率(见图4)。从该统计平均结果的意义来看，该频率空间分布图代表了每年9—10月份期间波弗特-楚科奇海各位置处发生有效波高大于各级浪高值的概率。

从图4可以看出，在1996—2016年夏秋季期间，大浪出现频率较高的区域位于楚科奇海以及波弗特海中南部海域，并从中心向四周递减。中部海域有效波高大于1 m的频率超过80%；大于2 m的频率在30%～40%；而大于3 m的频率在10%～15%。在波弗特-楚科奇海近岸海域，有效波高大于1 m的频率在50%～60%；大于2 m的频率在15%～30%；而大于3 m的频率在5%～8%。相比之下，尽管直观上感觉波弗特-楚科奇海北部海域的风区更长，大浪出现频率应该更高。然而，由于北部海域9、10月份还是存在大量的海冰，导致开阔水域面积不足，故该区域大浪出现的频率较低。

4 极值有效波高多年变化

为了了解波弗特-楚科奇海极值波高的多年变化和分布规律，本文将21年(1987—2007年)该区域9、10月份极值波高分别作区域平均和时间平均得到年极值波高的时间序列图(见5(a))和空间分布图(见5(b))。此处讨论的极值波高指的是SWAN输出的波弗特-楚科奇海各位置处每年9、10月份期间的最大有效波高，区域平均是指每年整个区域极值波高的平均，时间平均是各位置处21个年极值波高的平均。由图5(a)可见，1996—2016年波弗特-楚科奇海9、10月份极值波高呈明显上升趋势，极值波高的区域平均值从1996年的1.3 m上升至2016年的3.9 m，年均增长约0.09 m。空间分布上，极值波高的高值中心位于楚科奇海，数值上在4～5 m。考虑到极值波高的增加很可能与极值风速的变化存在显著的因果关系，故图5(a)同样给出了该海域区域平均极值风速的年变化时间序列图。然而，极值风速的波动趋势虽然与极值波高的波动趋势相近，但在数值上并没有显著增加。这说明极值波高的变化并不只受极值风速的影响，不能只由极值风速的变化来解释。结合近些年北极海冰减小的整体变化趋势，本文推测波弗特-楚科奇海极值波高的变化极有可能与海冰的变化也存在密切的联系。

为进一步验证该推测，本文分别将该区域各位置处9、10月份年极值有效波高(即最大值)与平均海冰密集度(即两个月的平均值)做线性回归，得到其年变化率，绘制空间分布图(见图6)。与图5(b)比较可见，尽管楚科奇海中南部海域的年极值波高值最大，但1996—2016年的增长率几乎为零，一些区域甚至为负，波弗特海南部海域的年极值波高增长率同样不高。相较之下，年极值波高较快增长的区域主要集中在波弗特-楚科奇海的北部海域，在1996—2016年间以0.1～0.2 m/a的速度增长，这也是造成图5(a)中区域平均的年极值有效波高增长的主要因素。在此前，Liu等[31]于2016年的研究表明，与图5(b)中对应的波弗特-楚科奇海北部海域，8、9月份的平均有效波高自1996—2015年的增长率为0.01～0.03 m/a。由此可见，整体上波弗特海年极值波高的年变化率明显大于平均波高的年变化率。

结合图6(b)中海冰密集度的变化可以发现，极值波高增长率最大的区域对应的海冰密集度衰减率也是最大的。在波弗特海中部和北部海域，其海冰密集度年衰减率在2%～5%。因此，1996—2016年9、10月份波弗特海中部和北部极值波高的显著增长，必然与海冰密集度的减小存在密切的关系。一方面，海冰的减少使当地的风浪有更大的风区得以成长；另一方面，海冰的减少也使得其对从外传来的涌浪衰减减弱。两个因素均有利于比以往更大的极值波高出现。而对于偏南部的海域来讲，距离海冰边缘区相对较远，海冰对极值波高的影响则有限，该区域的海浪已有足够的风区得以充分成长，乃至发展成为涌浪[1，8]。

5 极端海况下风—浪夹角

为了进一步理解波弗特-楚科奇海域极值波高的特点，本文将SWAN输出的21年(1987—2007年)9、10月份的谱峰波向与ERA-Interim再分析数据的10 m风向计算夹角，并进一步做时间平均，来体现波候尺度下谱峰波向与风向的关系(此处假设在风浪主导状态下，二者夹角不大)，所得到的结果如图7所示。从图中可以看出，夹角较小的区域位于波弗特海中部和北部以及楚科奇海东南部海湾，数值在75°～90°；夹角较大的区域位于楚科奇海东部沿岸及中部部分区域，数值在120°～130°。谱峰波向与风向的夹角较大也就意味了该海区存在显著的涌浪特征，该结论与Stopa等[1]基于波龄的分析结果基本一致。进一步来看，这也表明该海域极值波高的出现通常是风浪与涌浪叠加的结果，且根据对追算结果的整理发现，不同时刻谱峰波向存在显著的变化特征。

6 典型重现期计算

重现期波高常用的推算方法包括：Pearson Ⅲ型分布、Gumbel分布和Weibull分布等。其中Pearson Ⅲ型曲线的应用广泛，是中国水文气象计算中常用的频率曲线[32]。故在本文中，我们选择使用Pearson Ⅲ型曲线来计算波弗特-楚科奇海的重现期波高，其概率密度函数为：

(5)

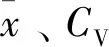
(6)

(7)

(8)

在水文计算中，若要求指出定频率P所对应的随机变量值xp，需要对密度曲线进行积分，即：

(9)

直接由(9)式计算P值十分麻烦，在实际应用中则是通过变量转换，得到关系式：

(10)

式中Φp为离均系数，通过查询得到。变差系数CV则由下式

(11)

得到。式中ki为实测值。CV皮尔逊Ⅲ型曲线的模比系数Kp值表，Kp表中不同的CS/CV值对应的离均系数Φp值不同，故视情况确定最优CS/CV值，对计算结果的准确性十分重要。

为确定最优的CS/CV值，本文分别选取楚科奇海中部和北部以及波弗特海中部的3个点，地理位置分别为190°E、69°N，190°E、73°N，210°E、75°N，绘制Pearson Ⅲ型曲线。取不同的CS/CV值，比较拟合结果，最终确定参数方案。

如图8所示，当CS=2CV时，各位置处Pearson Ⅲ型曲线对极值波高拟合的均方根误差最小，故本文选用CS=2CV方案，进一步计算该区域所有网格点的典型重现期有效波高[33]。

使用1996—2016年9、10月份的年极值有效波高数据，基于Pearson Ⅲ型曲线推算得到波弗特-楚科奇海重现期分别为20和50年的有效波高(见图9)。通过与图5对比，可以看出典型重现期的有效波高空间分布与极值波高(见图5(b))的空间分布具有一定相似性，且高值中心的面积更大，并向北扩张。楚科奇海和波弗特海的典型重现期有效波高水平相当，重现期为20年的有效波高在6.4 m左右(见图9(a))；重现期为50年的有效波高可达7.3 m(见图9(b))，同时高值区域面积相比图9(a)也有所增加，76°N以南的海域重现期为50年的有效波高基本介于6.0～7.0 m之间。波弗特-楚科奇海近岸海域重现期分别为20和50年的有效波高值差距不大，介于3.0～4.5 m之间。

由于风速对海浪的成长起着决定性的作用，因此为了对极值有效波高的变化规律有更加充分的认识，本文同样计算了典型重现期风速并考察了风速的多年变化。为保持一致性，适线法CS=2CV同样被采用于各重现期风速的推算。

本文对1996年—2016年波弗特-楚科奇海9、10月份的海表面风速进行了同样的处理，分别得到典型重现期为20和50年的风速分布。如图10所示，重现期风速的分布与重现期波高的分布图9有较好的一致性，重现期波高的高值区域对应的重现期风速也较大。楚科奇海-波弗特海重现期为20年的风速值在20 m/s以上，最大值在25 m/s左右(见图10(a))。相比之下，重现期为50年的风速分布高值区域在面积上更广，且向北扩张；在数值上，楚科奇海-波弗特海重现期为50年的风速值在25 m/s以上，最大值在27 m/s左右(见图10(b))。然而图9中，76°N 以北海域重现期为20和50年的有效波高则明显较小，尤其是140°W以东、76°N以北的区域，其多年一遇的极值波高甚至可小于1 m。该现象难以通过不同重现期极值风速的空间分布来解释，因为通过图10可以发现，该区域的各重现期风速值与其他区域的差别并不显著，在重现期为20和50年的两种情况下均可以达到20 m/s左右。因此，本文初步推测该区域重现期波高水平不显著的原因，是该区域每年9—10月份仍存在大量海冰，抑制了海浪的生成和传播。

为了验证该推测，图11给出了1996—2016年波弗特-楚科奇海9、10月份平均海冰密集度的空间分布。很显然，波弗特海东北部海域存在较多的海冰，这无疑会抑制海浪的生成和传播，因而造成夏秋季不同重现期波高均较小，因此该结果也说明除了海表面风速之外，波弗特-楚科奇海不同重现期极值波高的变化同样也会受到海冰变化的影响，且纬度越高的海域受海冰影响越显著，倘若忽略海冰的影响，推算得到的多年一遇极值波高将会显著偏大。

7 结论

为进一步了解波弗特-楚科奇海的波候特征，本文利海浪模式SWAN对1996—2016年波弗特-楚科奇海夏秋季(9、10月份)海浪进行了数值追算，基于对计算结果的统计分析和Pearson Ⅲ型曲线的极值推算，量化了该海域极值海浪的时空分布与变化特征，并讨论分析了海表面风以及海冰对该海域极值波侯的影响。主要的研究结论如下：

(1) 波弗特-楚科奇海大部分海域有效波高大于1 m、大于2 m和大于3 m的频率分别在70%、30%和10%左右，其中大浪出现频率最高区域为楚科奇海中部海域。大浪发生概率自波弗特-楚科奇海中南部海域向四周海域逐步减小。

(2) 波弗特-楚科奇海的平均年极值波高的高值中心位于楚科奇海中南部海域，通常超过5 m，但是年变化率很小，几乎为零。相较之下，波弗特-楚科奇海北部海域的年极值波高年增长率较大，每年约为0.1～0.2 m。

(3) 波弗特-楚科奇海中部大部分海域重现期为20年的有效波高在6.4 m左右；重现期为50年的有效波高在7.3 m左右，且该有效波高是涌浪与局地风浪共同叠加的结果。波弗特-楚科奇海近岸多年一遇的有效波高约为3.0～4.5 m。

(4) 波弗特-楚科奇海的极值波候会受到海表面风与海冰变化的共同影响。对于偏北部海域而言，由近年来海冰减少所引起的开阔水域增加，导致极值波高呈显著上升趋势。相比之下，中南部大部分海域9、10月份几乎无冰，故极值波候主要受风速影响并与风速的变化基本一致，同时由于开阔水域面积较大，该海域的极值波高与各重现期波高在数值上都处于较高水平。

在以往波弗特-楚科奇海针对平均有效波高的研究基础之上，本文进一步量化和讨论了该海域极值波高的时空分布与变化特征，对于进一步理解该海域强海况下的海浪特点有十分积极的意义。另外，本文所采用的模式配置同样还具备服务于该海域数值预报应用的潜在价值。不过，本研究也依然存在着一定的局限，除了模式本身、强迫场的分辨率对于结果的影响之外，本文在近岸浅海的模拟结果依然缺乏可靠的检验，这些都可能会给结果带来一定的不确定性，需要在未来的研究中进一步完善。