基于三维外形扫描的间隙阶差自动评定方法

解文序，朱运东，林雪竹

（长春理工大学 光电工程学院，长春 130022）

在传统的制造业中，设备零部件组装时，如果零件尺寸误差较大会导致安装部件之间存在较大的缝隙，影响部件的外观、密封、风噪等［1］。为提升产品的质量，必须对装配的间隙、阶差特征做到精确、稳定、有效的测量［2］。传统的人工测量方法主要有塞尺、面差尺测量等方法，存在效率低、精度差、结果易受主观因素影响等缺点［3］。近年来，数字化测量技术发展迅速［4］，因系统非接触性、精度高及柔韧性好等优点，广泛应用于间隙阶差的检测。

目前，国外在间隙阶差测量领域发展十分成熟，在激光线三角测量方向表现最为突出。KOSMOPOULOS等人［5］提出了一种立体摄像机的测量系统，利用CCD相机接受反射光以获取间隙阶差信息。TRAN等人［6］开发了一种基于视觉的非接触间隙和阶差测量系统，通过多线结构光发射器和高分辨率相机，采用自适应激光条纹，能够处理表面复杂、反射性差的目标。相关测量设备有美国Orgin Technologies公司的Laser Gauge系列和英国的Gap Gun产品等。

国内对间隙阶差视觉检测技术的研究也多有进展。严成等人［7］采用了一种基于三维激光扫描的检测方法，提炼出了计算蒙皮对缝间隙阶差的数学模型，验证了计算精度，但此方法仅靠欧氏距离求解，对点云预处理过程要求严格，可靠性较差。张波等人［8］提出了一种基于支持向量机的（Support Vector Machine，SVM）三维对缝点云间隙阶差提取方法，验证了算法的精度和稳定性，对曲率过大的点云适应性较差。在间隙阶差测量应用方面，国内工业上主要引进国外成熟产品进行应用，自主研发设备少有投入工程应用中。

而在工程实践中，面对复杂多样的间隙阶差类型，工人需根据经验判断模型类别并选取测量方法，这增加了人为操作带来的不确定性。因此，为了实现间隙阶差类型的自动识别与检测，实现对缝测量的数字化过程，首先，利用工业线结构光扫描系统对部件进行外形扫描，得到对缝点云，再对点云数据预处理，获取待测部件点云模型；其次，基于三角形顶点法矢估计理论，通过对采样点一阶邻域三角形法矢加权平均求得采样点法矢，并对其进行高斯映射聚类，划分间隙阶差类型；最后，提出不同类型的模式点识别方法，通过计算法向夹角阈值，得到待求特征点，建立间隙阶差求解模型。通过实验验证对缝间隙阶差求解的精度及可靠性。整体流程如图1所示。

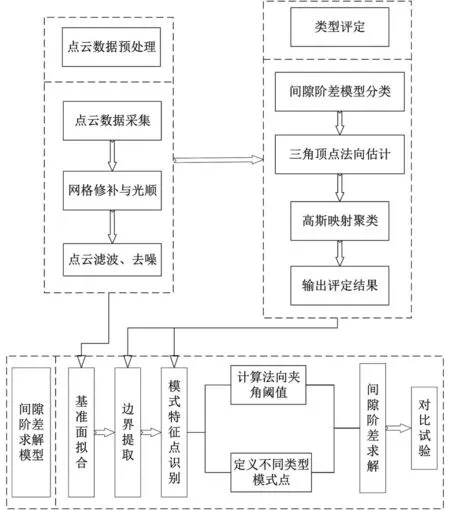
图1 整体流程图

1 对缝扫描数据预处理

近年来，点云处理技术是一个发展非常快速的领域，应用于机器人感知、机器人自主精确定位、机器人导航、三维重建、智能驾驶等领域［9］。扫描对缝得到的三维点云数据，受仪器设备、扫描环境及部件结构等因素影响，数据中包含噪点、离群点等杂点，因此，为了获得高精度符合要求的点云数据结构，需要对采集的数据进行预处理。

1.1 原始网格数据预处理

采用线结构光扫描设备获取的点云数据为三角化点云，其在工业三维测量领域应用广泛。扫描仪获取的数据中伴有杂点或噪声［10］，数据预处理的结果对后续计算起着至关重要的作用。对于超出预定扫描区域的离群数据，借助交互软件手动去除；对于噪声数据，采用网格滤波及光顺的方法处理；对于存在的孔洞缝隙等采用孔洞修补与边界缝合相统一的处理方式［11］。通过对三角化网格模型的预处理，得到符合要求的待测点云数据。网格模型处理结果如图2所示。

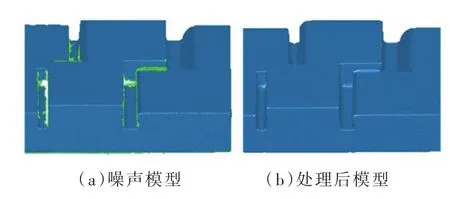
图2 网格噪声及处理后模型

1.2 点云滤波处理

不同设备获取的点云噪声结构也不同，为了去除点云中包含的杂点，解决重复扫描造成的点云分布不均问题，需采用点云滤波处理。常用的滤波处理方法有高斯滤波、均值滤波与双边滤波等。为了实现噪声去除与数据简化，采用PCL中的统计分析滤波法（Statistical Outlier Removal）处理原始点云。从三角网格中提取点云的三坐标，对每个点pi，计算它到它的所有临近点的平均距离Ei，临近点的数目可自行设置。将得到一个正态分布的数据结果，平均距离在标准范围（由全局距离平均值和方差定义）之外的点，可定义为重复扫描得到的点云噪点，可解决点云密度分布不均问题。

所得到的三角化点云有序分布，为了更好地进行后续间隙阶差模型求解，扫描过程需按照一定规范进行，得到的线式点云模型如图3所示。

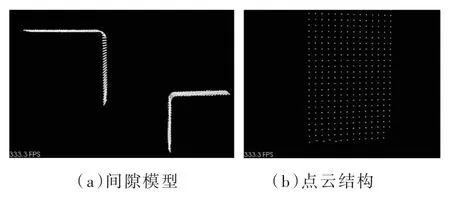
图3 点云模型

点云结构基本有序，通过后续点云处理，可实现对缝间隙阶差检测。

2 间隙阶差评定模型

在进行工业三维对缝间隙阶差检测时，为了减少人为操作带来的误差，更好地实现自动化检测，以三种间隙阶差类型为研究对象，通过改进三角形顶点法矢求取方法，基于高斯映射聚类特征识别理论，将单条扫描线点云进行特征识别，通过设定阈值实现模型自动评定。

2.1 对缝类型

按照间隙阶差DTS（尺寸技术规范）［12］可知，工业零部件间隙阶差通常可划分为垂直线形、锐角线形、钝角线形三种类型，如图4所示。

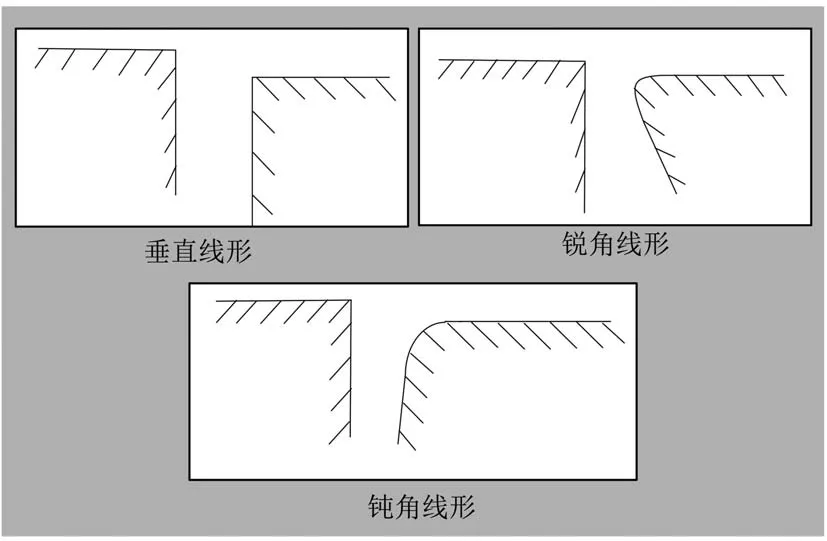
图4 间隙阶差类型

当翻边角度发生改变时，其计算方法多有不同，所得到的结果也有较大差异，如图5所示。

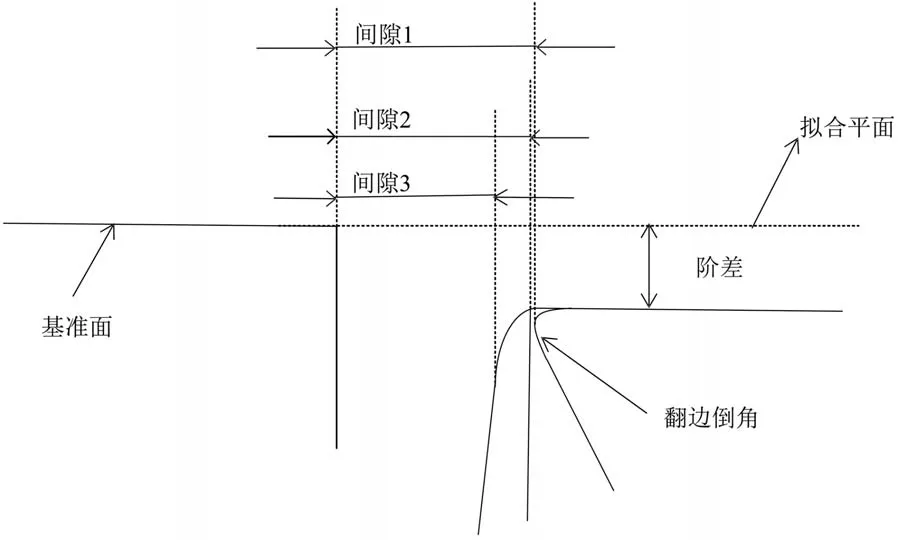
图5 不同类型倒角的间隙阶差计算

图5显示了不同翻边倒角情况下的间隙阶差求解算法的区别，不同类型对缝的间隙阶差求解差别较大，因此，对不同对缝类型的间隙阶差进行识别分类，可求得更加准确的间隙阶差值。

2.2 基于法向提取的对缝特征预处理

通过求取数据点一阶邻域点所构建三角形的法矢，求取其加权平均值，可得到采样点的法矢［13］。依次求取对缝两侧点云法矢。具体过程如下：

（1）将对缝两侧点云划分为M个包含N个点的区域。依次选取采样点，分别建立多个以采样点vi为中心的球体。将球体内的点映射到过采样点的任一平面上，以任意一点为起始点，按顺时针方向依次排序，得到索引集VIP。

（2）图6为其中一点vi的一阶邻域，包含N个三角形法矢。其中，Nvi为vi的单位法向量，ei,j、ei,j+1为三角形的两条边，NFk为三角形的法向量，Gk为顶点到质心gk的距离。则三角形Fk的单位法矢量为：

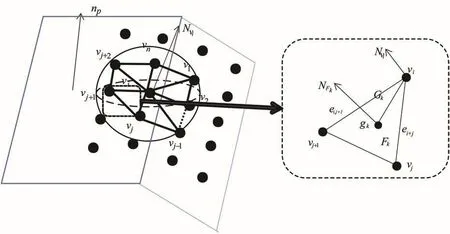
图6 采样点一阶邻域顶点法矢估计

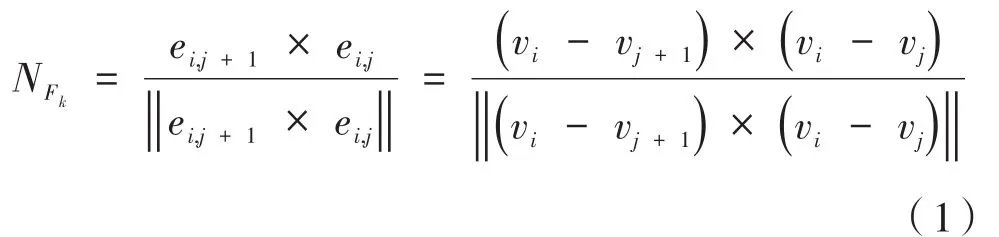
（3）可求得任一点vi的单位法向量为：

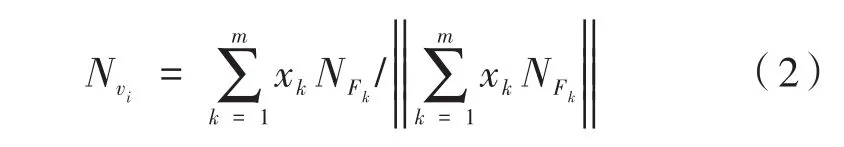
（4）可求得采样点的单位法矢ni为：

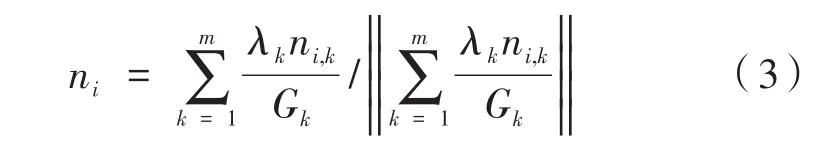
2.3 对缝模型评定

为了识别对缝特征，将对缝侧采样点的法矢进行高斯映射。文献［13］等均采用将采样点邻域三角形的法矢作高斯映射，得到关于采样点的特征信息。通过式（3）对采样点邻域三角形的法矢加权平均，求得采样点法矢，并对采样点法矢做高斯映射聚类，以实现特征识别。

对缝单侧采样点的高斯映射定义为每个点的法矢映射到以原点O为球心，半径为E的单位球体 S2上［14］。即：

不同曲面上点的高斯映射是不同的：对于平面上的点，高斯映射是一簇；曲面上的点，高斯映射为散乱分布在球体上；对于在两个曲面交线上的点，高斯映射为两簇点［15］。对于倒角特征，其映射为球上的圆弧。钝角类型的点云映射在球面上分布的角度小于90°；锐角类型的点云映射在球面分布的角度大于90°；直角类型的点云映射在球面上呈大致90°的两簇点，具体效果如图7所示。

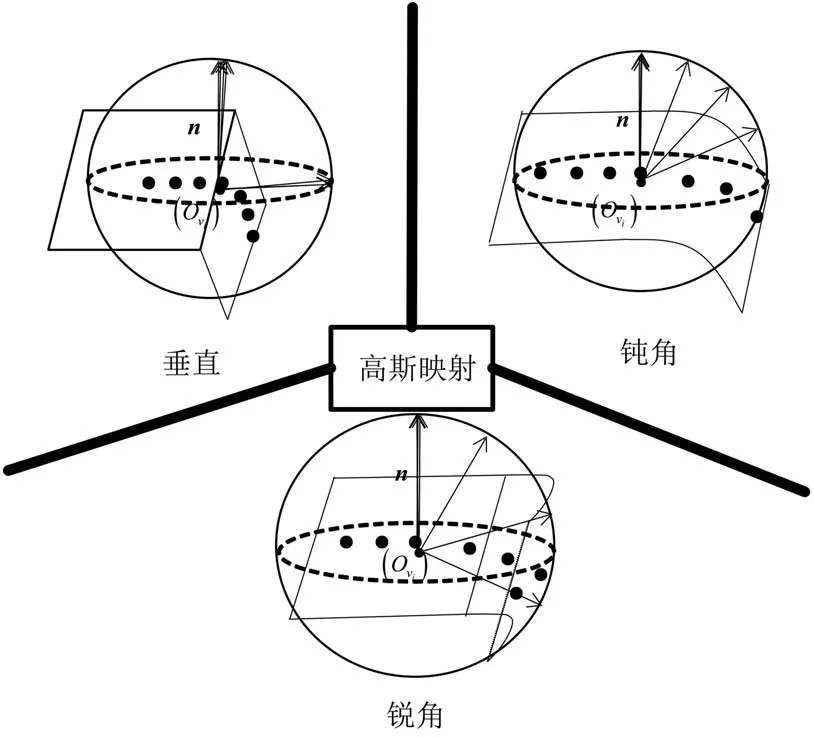
图7 点云高斯映射

对采样点进行高斯映射后，因高斯球是以原点O为球心，且其半径为E，所以采样点的单位法向量ni即为映射后点坐标pi，对映射后的点进行聚类分析。

设单位高斯球上两点pk、pl的测地距离为：

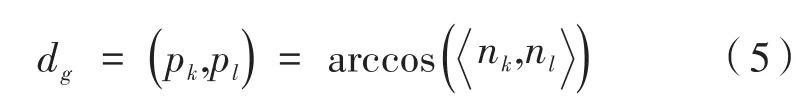
其中，k,l∈Ip。文献［15］中用两个聚类的平均距离Dc来定义两个聚类的测地距离：

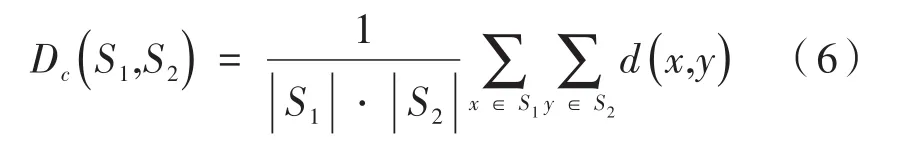
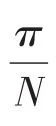
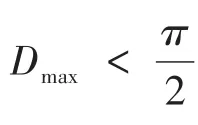
3 对缝间隙阶差求解模型

对缝间隙阶差求解过程中，基准面的拟合，边界点的提取，计算区域的选择及计算模型的建立，都会对最终结果的精度产生重大影响。

3.1 对缝基准面拟合

对缝两侧表面特征往往很复杂，在间隙阶差数据处理的过程中，对于基准面拟合，需要指定区域［16］以减少计算量。在实际工程中，一般待测物体的中心点为坐标原点，前后为x轴方向，上下为z轴方向，左右为y轴方向，在求解过程中，以待测物体坐标轴负方向一侧为求解基准面，根据对缝实际情况，沿扫描线方向，初步选取对缝两侧点云各10 mm的点云，y轴方向宽度3 mm，z轴方向10 mm。

对基准面子点云进行平面拟合，为后续模型评定及间隙阶差求解做好准备工作。

目前基准面拟合方法主要有稳健特征值法［17］、改进的 RANSAC 算法［18］等。采用一种正交最小二乘法拟合基准面，其以三个方向坐标的残差平方和作为目标函数来求得最优解，兼顾三坐标误差［19］，在文献［19］的基础上改进了拟合方法，通过实验验证，该方法对复杂平面具有较强的适应性。

针对间隙阶差点云模型实际情况，提出了一种改进的拟合方法，具体步骤为：

（1）输入点云，根据正交最小二乘平面拟合方法，可得拟合平面α的参数a、b、c的值。

（2）计算点云数据pi到拟合基准面α的距离di：

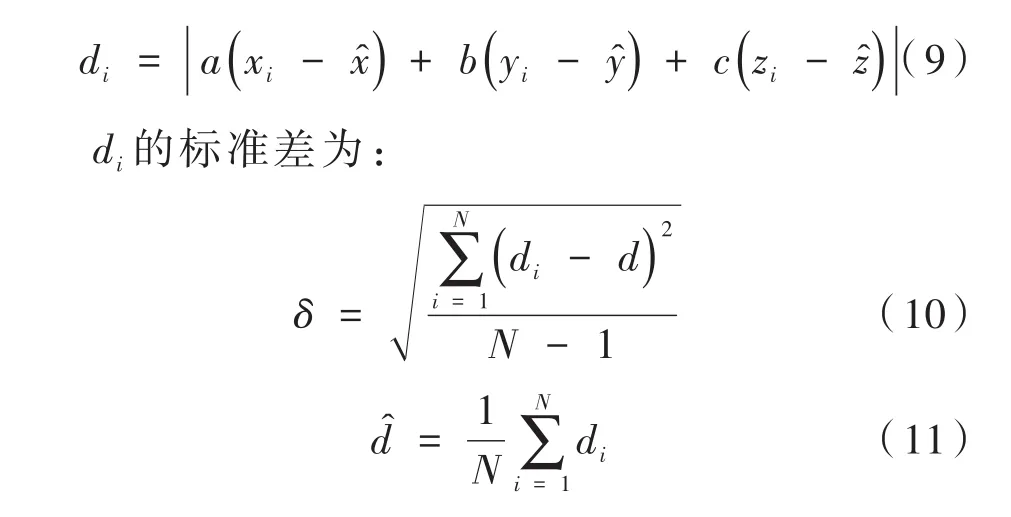
（3）当di＞3δ时，此点被认为是异常点，删除；反之，保留。

（4）利用所有保留下来的点重新计算a、b、c的值。

（5）重复步骤（3）～步骤（6）过程，直到所有点都在阈值范围之内。

此时计算得到的拟合平面即为最佳拟合基准面，拟合效果如图8所示。

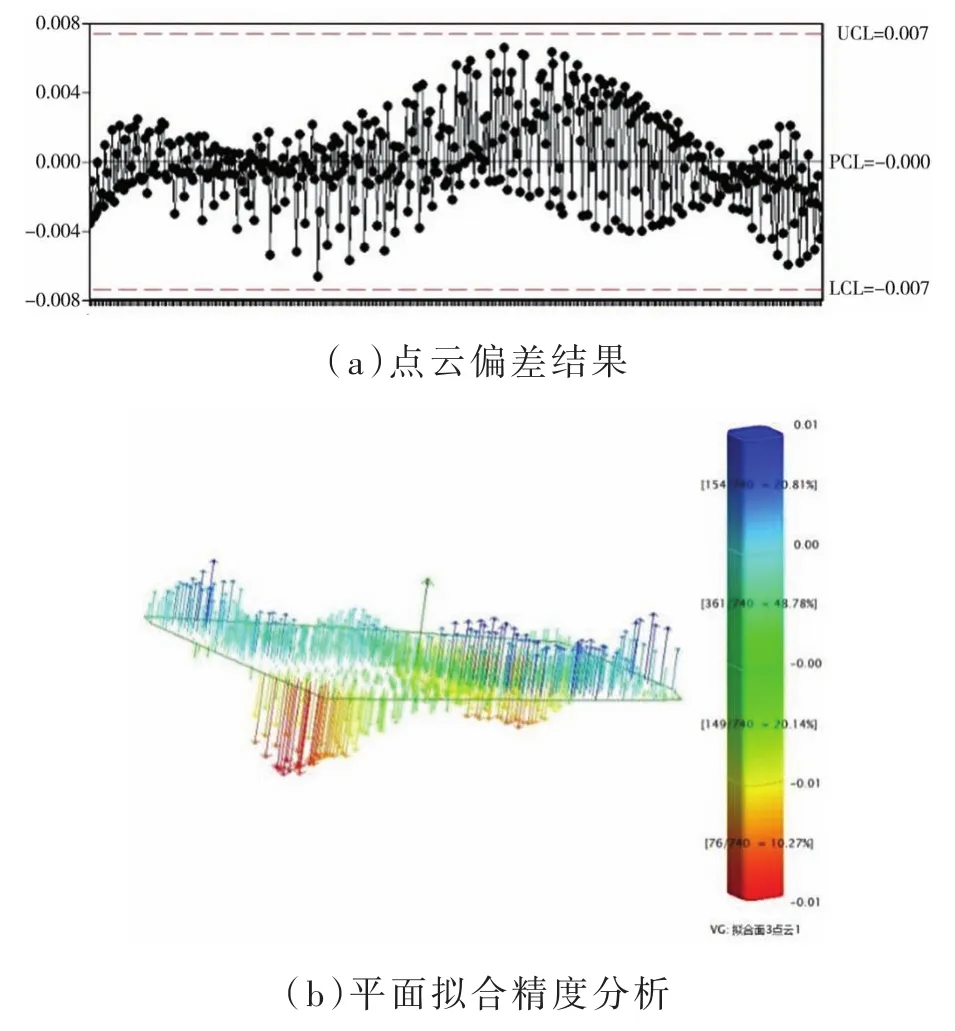
图8 基准面拟合

图中UCL代表控制上限，LCL表示控制下线，PCL为控制中心线，δ为标准差。其对应关系如下：

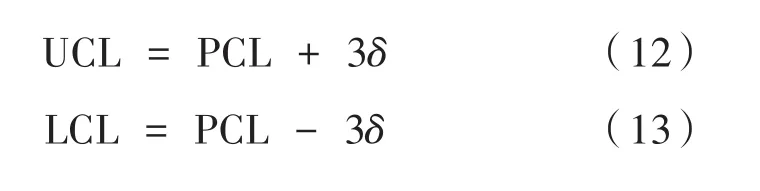
式中，PCL=0，可得基准面拟合精度在0.01 mm以内，符合精度要求。通过此方法获得的属于基准面的点用于后续法向计算，可克服基准面不平整的情况，提高了后续模型计算的准确度。

3.2 对缝边界点提取

对缝边界点的提取是后续包围盒及模型自动求解的前提条件，对模型计算精度有着至关重要的影响。

根据上节中求解得到的点云法向，分别计算不同对缝类型基准面中单条扫描线点云法向与基准面法向αp之间的夹角，所得结果如图9所示。

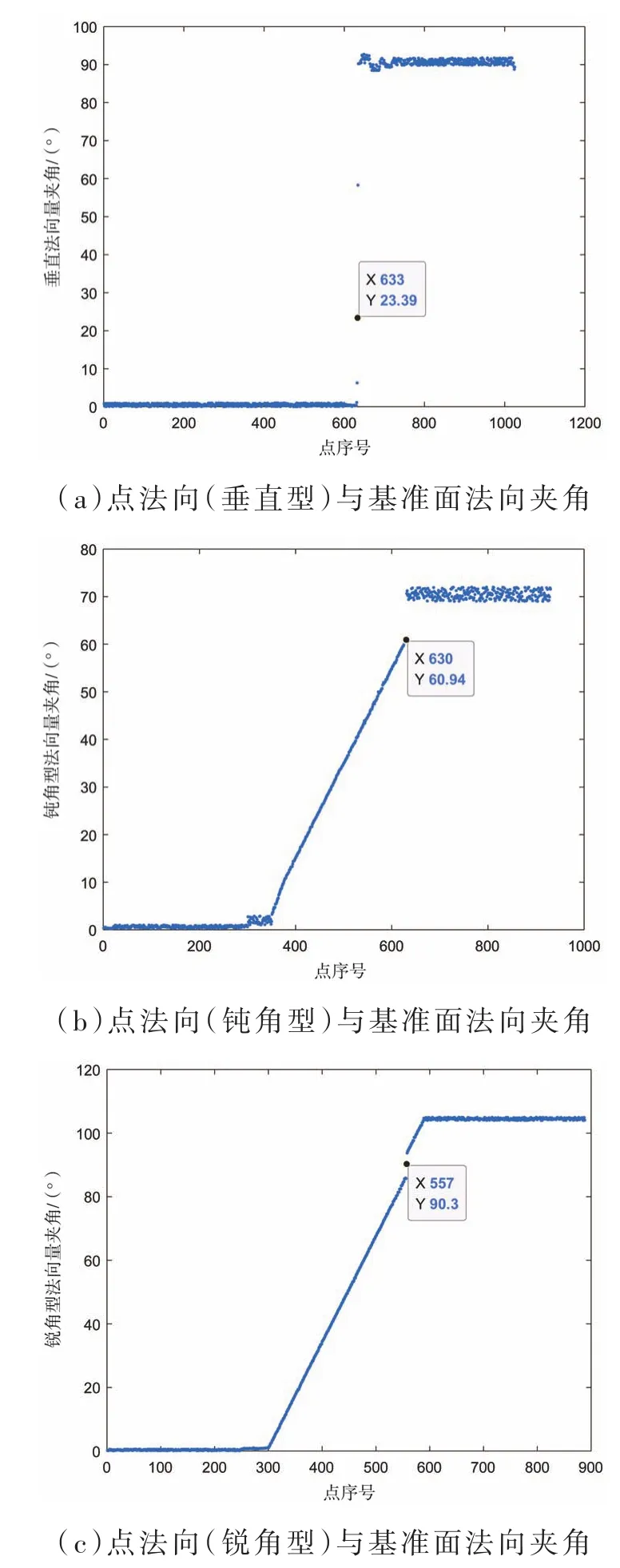
图9 不同模式点法向偏差夹角

由图9分析可知：

（1）垂直线形点云在棱角边界处，点云与基准面法向夹角快速增大，相邻点之间法向角度相差较大。

（2）钝角线形点云在边界处相邻点法向夹角变化较小，当翻边角度变化趋于停止时会出现角度拐点，之后夹角值迅速趋于稳定。

（3）锐角线形点云在边界处夹角变化与钝角型一样，在法向角度90°附近极小范围内会出现变化较大的特征点。

根据图（9）总结的规则，可快速提取单条扫描线的基准面边界点。为了实现求解的自动化过程，根据所求边界点，构建包围盒［8］进行详细划分。

设包围盒y轴宽度W为15条扫描线间距，x轴长度为L及z轴高度H可根据具体表面情况设置适当阈值，包围盒最重要的两个顶点为且满足H。包围盒内点满足xmin≤ x≤ xmax，ymin≤ y≤ymax，zmin≤z≤ zmax，选取基准面任意一个边界点作为包围盒坐标原点p，基准面单位法向量为z轴，扫描线方向为x轴，其单位法向量为，可得y轴单位法向根据右手定则可建立其坐标系，将对缝侧扫描线沿Y轴由小到大排序，得到扫描线lk～lk+14(0 ＜k≤m-14)，其中m为扫描线总数，k为扫描线序号。于是，可知包围盒内的点为pi,j(k ≤i≤k+14,0＜j＜n)，其中n表示第一个曲率差大于给定阈值的点序号，包围盒建立情况如图10所示。

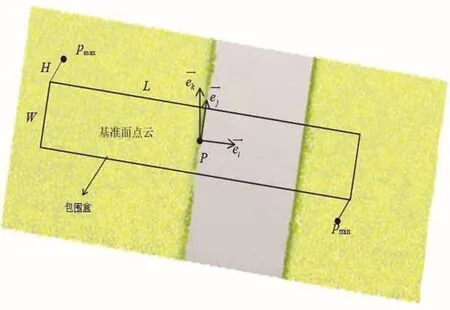
图10 包围盒选取待测点云

3.3 对缝求解模式点识别

对缝求解模式点包括点云中的边界点和倒角处的特征点。

假设pi和pj为模式点，则两个点的单位法向量ni与nj(i , j＜m)的法向夹角余弦值为：

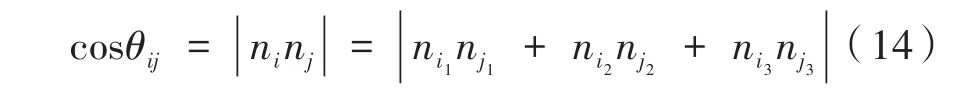
对其进行反余弦计算可求得夹角值为θi,j。

针对点云法向夹角的变化，定义了如下模式点识别方法，具体过程为：

（1）定义模式点识别范围

包围盒内扫描线点云序号为pi,j(k ≤ i≤k+14,0＜j＜n )。定义包围盒内对缝负方向表面为基准面，将基准面内pk,1点作为初始点。

（2）法向夹角阈值计算

依次计算每条扫描线上属于基准面(di＜ 3δ)的点法向与基准面法向夹角，记为θi,j，对夹角从小到大进行排序，夹角最大的点即为基准面上的边界点（由法向求取方式决定，可参照图9，将此夹角记为 σi，i为扫描线序号(k ≤i≤k+14)。将σi作为分割基准面与其他相接面的角度阈值。

（3）定义不同类型模式点

识别出阈值后，依次计算扫描线上相邻两点间法向夹角，每条线点云都可获得一个法向夹角序列Xk,m，每一个序列包含2个相邻点，不同的间隙类型有不同的划分方式，具体如下：

①对于垂直线形点云：对缝两侧角度阈值σi所确定的边界点即为模式点h1。h1同时为间隙与阶差的特征点。

②对于钝角线形点云：σi所确定的边界点即为阶差模式点f2；对于间隙求解，以其位于基准面一侧为例，计算点云法向夹角。因钝角上各个位置点处法向变化不一致，当出现Xi,g+1＜ςi＜ Xi,g时(ςi→ 0)，则Xi,g+1所含点pg+1即为所求间隙点g2。

③对于锐角线形点云，阶差模式点f3获取方法同钝角形点云一样；对于g3求解，可将其所在线点云中属于拟合面的点投影到拟合面上，将投影点拟合成直线，拟合直线的方向向量为L，依次求取剩余点法向与L之间夹角，并对其进行比较，夹角最小的点即为模式点g3。

（4）根据上述步骤可得出对缝模式点的识别过程，如图11所示。

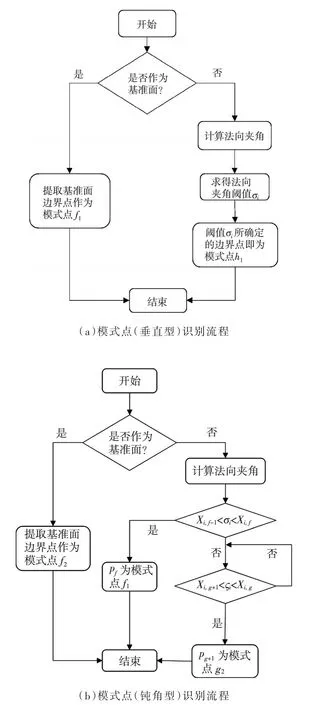
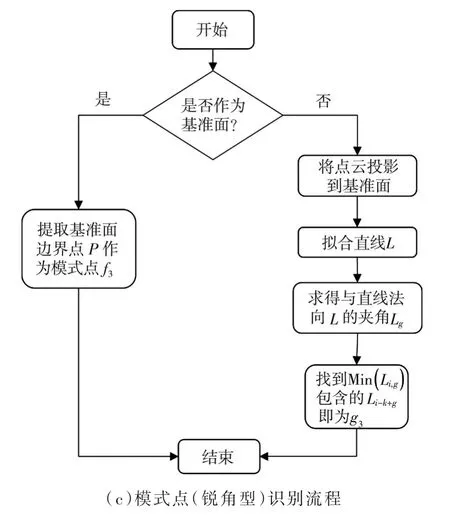
图11 不同类型模式点识别方法

3.4 模型求解计算

对于模式1间隙阶差计算，选取两平面交点作为特征点计算间隙阶差，对应于模式点h1，计算模型如图12（a）。将间隙两侧模式点h1(x1,y1,z1)、h2(x2,y2,z2)分别投影到基准面α上，得到两 个 投 影 点 h＇1与 h＇2，则 h＇1、h＇2之 间的 距 离 即为间隙值。

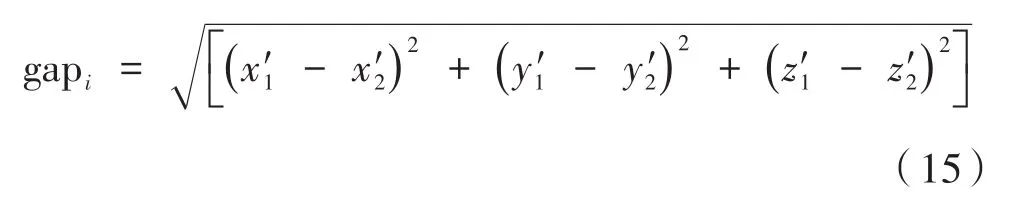
扫描线点云之间存在一定点间距a，根据点云结构可知，其最大误差为2a，所以有：

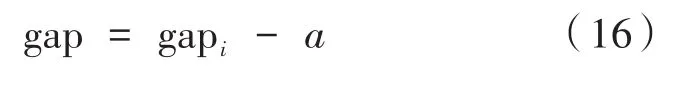
对于阶差计算，为模式点f1到拟合基准面的距离：

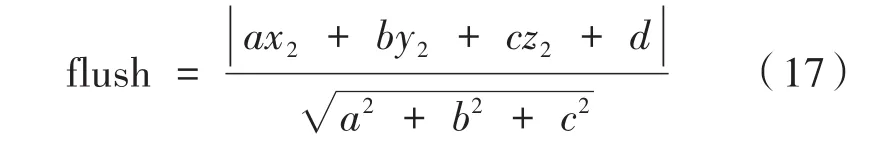
对于有翻边倒角的间隙特征，计算过程同式（16）。模式2为间隙计算模式点圆角根部与下表面的交点g2，模式3为倒角处法向变化最大的点g3；对于阶差，计算过程同式（17），模式2阶差计算的模式点为 f2，模式 3 为 f3，如图 12（b）、图12（c）所示。

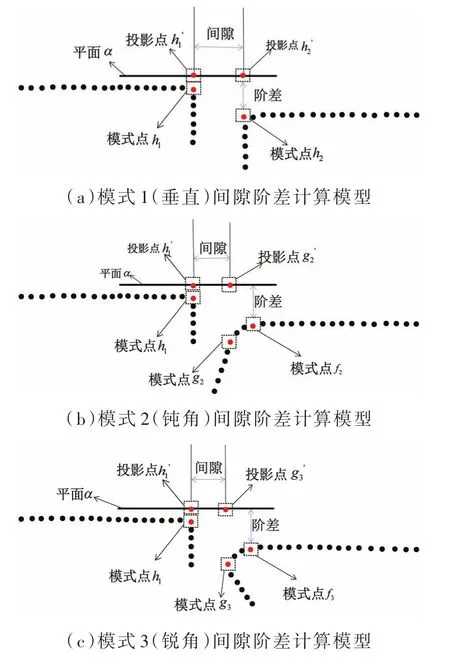
图12 不同模式间隙阶差计算模型

4 实验与分析

4.1 测量实验

此次实验以图（13）间隙阶差标准量块为测量对象，采用线结构光扫描系统获取原始数据，精度为0.05 mm，点间距0.1 mm。包围盒大小定义为宽度W=3mm，长度L=15mm，高度H=10 mm。利用文中提出的方法，可实现间隙阶差模型评定及求解。此方法虽然对相应模型具有很强的适应性，但应特别注意间隙阶差求解及评定参数阈值的定义。另外，当对缝处实际间隙阶差模型非常复杂时，可通过修改包围盒范围与调整相应阈值实现求解。

图13 标准量块

通过测量求解所得结果如表1所示。

选取包围盒内15条扫描线，通过求解其平均值作为最终测量结果，减小了误差，使测量数据更有说服力。通过表1可知，三种对缝模式的阶差测量误差分别达到了0.013 mm、0.019 mm、0.019 mm，垂直线形测量误差最小；三种对缝类型的间隙测量误差分别达到了0.022 mm、0.029 mm、0.027 mm，均满足工业0.1 mm的对缝测量误差要求。间隙误差结果比阶差整体要大，通过分析求解过程，总结原因有：测量线出现偏差、特征点处点间距与平面上两点之间点间距有差别、倒角处标准件加工误差等。

表1 对缝间隙阶差求解结果

测量误差结果如图14所示。

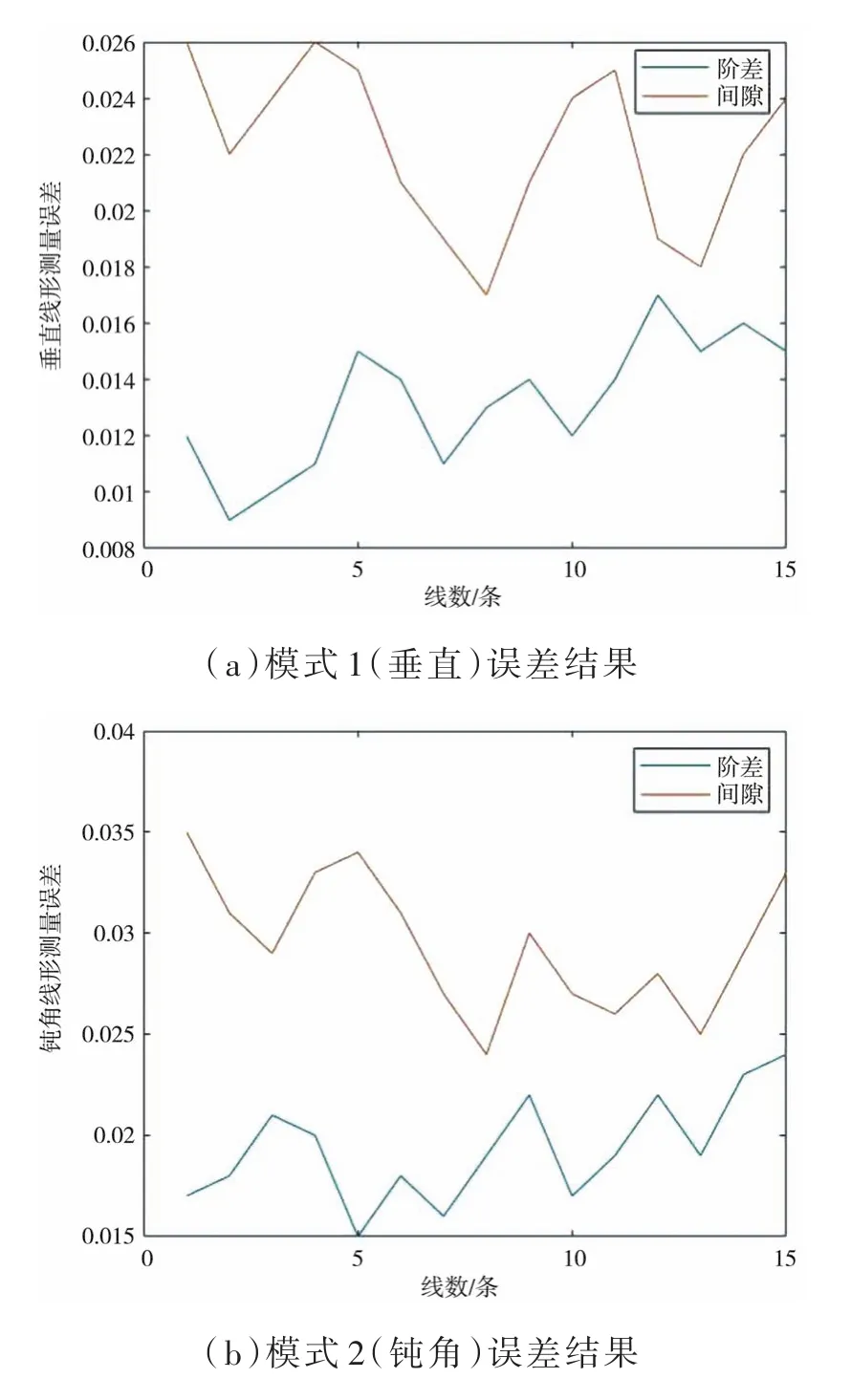
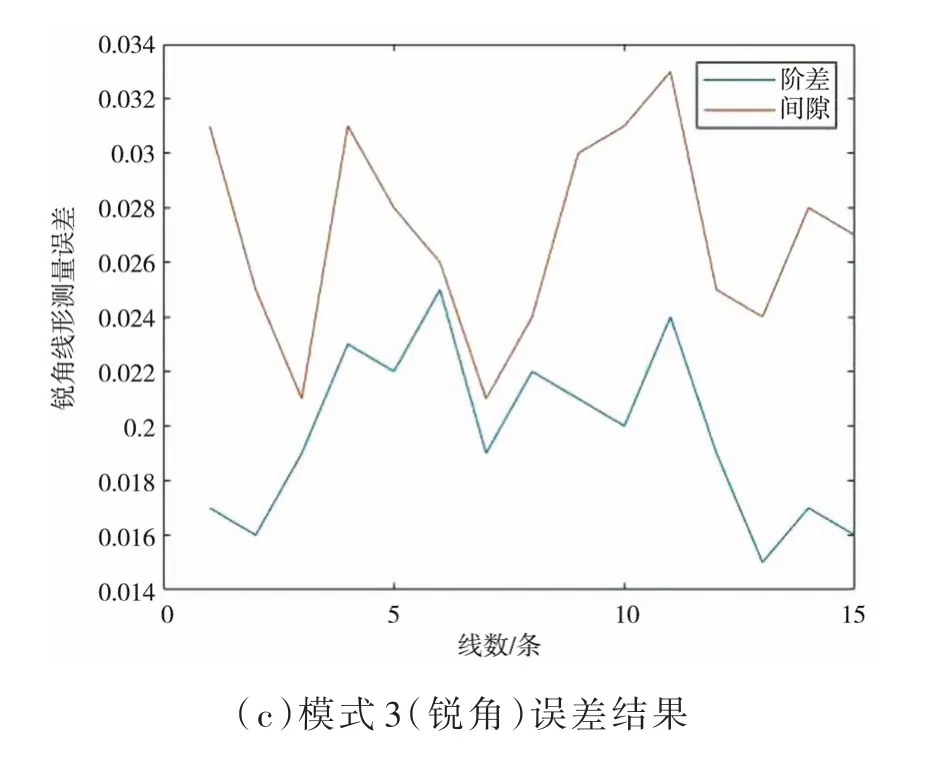
图14 测量误差结果

4.2 对比试验

在工程实际三维测量过程中，为了实现间隙阶差的在线数字化测量与分析，往往通过人为经验判断类型并选取测量特征点，这将忽视待测部件特征信息，引入误差，影响最终结果的准确性。将其与文中自动识别方法进行对比，误差结果图如图15所示。

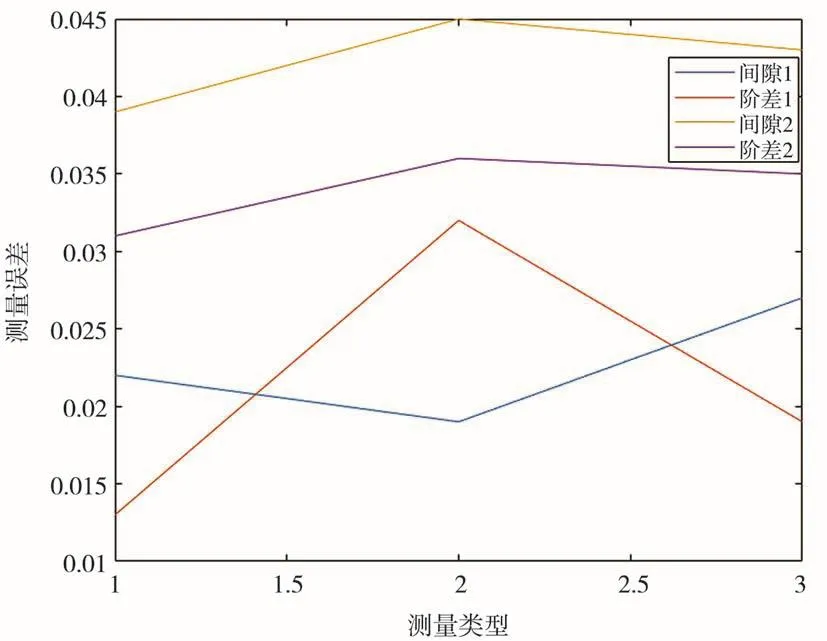
图15 对比实验图

其中1为人工选取特征点所得测量误差，2为文中自动评定测量误差。由图15可知，人工选取特征点得到的测量结果误差明显大于文中自动评定得到的结果，证明了文中方法的可行性。

5 结论

文中方法实现了对不同类型间隙阶差的自动评定检测。（1）此方法实现了点云数据预处理，通过网格与点云数据预处理剔除了噪点；（2）实现了采样点法矢重构，输出了间隙阶差类型评定结果；（3）提出模式点识别方法，实现了间隙阶差模型求解；（4）最后通过与人工选取特征点的测量方式进行对比，经过对比分析，文中自动评定的测量方式精度更高。但此方法也受限于多种因素，其中包围盒的选取、点云预处理过程、对缝侧点云结构等因素都会对最终结果产生影响。后续研究可通过机器人路径规划、改善操作环境、精确计算特征点间距等提高测量准确度。