军事评估中一致性悖论问题研究

狄继超 张东戈 牛彦杰 禹明刚

（陆军工程大学 指挥控制工程学院，江苏 南京210007）

1 引言

现代军事决策高度依赖数据，如果数据存在偏差悖论，基于数据的决策就会有系统性偏差。面对各类数量庞大、种类繁多的数据，指挥员与参谋人员习惯使用汇总后的数据来判断态势、做出决策。然而实践发现，在“汇总”数据时，有时会出现数据分类汇总与合并汇总所获得的结果不一致的现象，这就是辛普森悖论（Simpson's Paradox）。

1951 年Simpson E 发现了这种统计不一致的现象。这一现象具有普遍性，引发了不同领域学者对这一问题的研究兴趣。Bickel 等研究了研究生招生中有关性别偏见的辛普森悖论问题［1］；王艳军等研究了软件质量评估中的辛普森悖论现象［2］；Norton 等以实例解释了为什么会发生辛普森悖论并提出了避免措施［3］；Alipourfard 等讨论了在二进制因变量数据集中识别辛普森悖论的方法［4］；Vilenchik 对社交媒体数据中存在的辛普森悖论进行了研究，并设计了一个统计框架去发现其中存在的问题［5］。在军事领域目前缺乏对辛普森悖论的相关公开研究文献。

随着我军现代化进程的持续推进，基于数据的各类军事量化评估、决策越来越普遍，如何发现和处理辛普森悖论，也日益成为提升军事评估、军事决策可靠性和有效性的一个突出现实问题。

2 辛普森悖论产生的原因

图1 用两型坦克打击目标的统计图来说明辛普森悖论产生的原因。横坐标表示上级安排的打击目标数，纵坐标表示命中数，每个点对应的向量的斜率就是命中率。两种坦克分别对一类目标和二类目标进行打击，如果对一类目标的命中率记为k1，对二类目标的命中率记为k2，总体的命中率记为k。，则有如下计算公式。

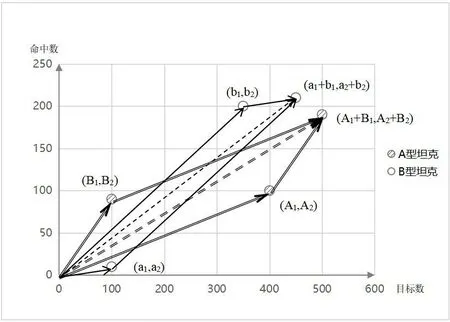
图1 辛普森悖论原因示意图

对于A 型坦克：

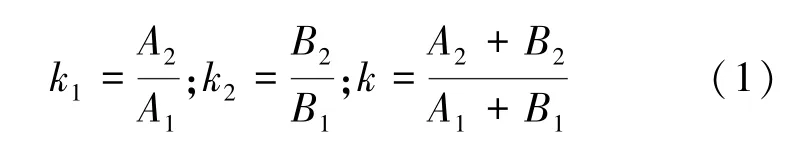
对于B 型坦克：

命中率比较：

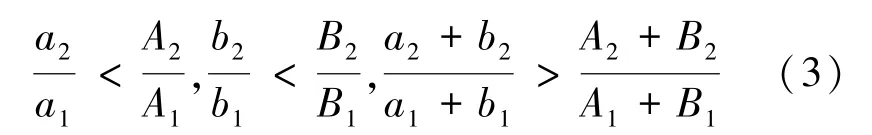
由式（3）可以发现，对于一类目标和二类目标，A 型坦克命中率均低于B 型坦克；但计算总命中率时，却发现A 型坦克命中率高于B 型坦克。这种统计方法只简单地做数量上的加法，对不同目标类型不加以区分，忽略了命中不同类型目标的难度差异，就容易造成辛普森悖论。

由此可知，就军事评估和决策问题来说，引发辛普森悖论的因素是存在易被忽略的混杂变量，也就是数据在获取时，存在隐形的获取差异，导致不同条件下分组所包含的“难度权重” 信息丢失，最终得到错误的结论。

3 辛普森悖论检测方法

根据辛普森悖论产生的原理，可以通过检测变量在“汇总数据”中和“分组数据”中的趋势变化是否一致来判断是否存在悖论。

趋势对比检测法（Trend Contrast Detection，TCD）具体可以分为三步。①在混杂变量上将数据分解成同质性更好的子组。②采用线性拟合刻画自变量和因变量之间的相关变化趋势。③通过对比汇总数据中的趋势与子组数据中的趋势是否一致来判断悖论是否存在。

3.1 基于差异分组法的数据分组

数据分组面临的最重要的问题是分组之间的界限确定。对于定性性质的数列，例如坦克命中率对比评估，组限的确定比较简单，只需要将打击目标按照难易进行分组。在复杂战场环境下，组限的确定可能会比较复杂，如射击若按能见度、机动速度等设界，就会没有明确的组限分割标准，此时就需要通过分析数组中数据的值来确定分组。

3.1.1 确定分组目标

假如评估目标是统计分析因变量y随自变量x变化的变化趋势。采集数据样本总量为n组，x的数值集合X ＝｛x1，x2，…，xn｝，y的数值集合Y ＝｛y1，y2，…，yn｝。数据统计中存在着混杂变量xc的干扰，xc的数值集合为XC ＝｛xc1，xc2，…，xcn｝，混杂变量xc的值域［min（xc），max（xc）］。

根据混杂变量分区，分组内容见表1。分割混杂变量值域将数据共分成m个子组，每组依次表示为b1，b2，…，bm。在分组中p为划分后的混杂变量的分区，它是一个混杂变量的值域空间，依次表示为p1，p2，…，pm。设sh（h ＝1，2，…，m -1）为各分区之间的组界，sh∈XC。ni（i ＝1，2，…，m）为第i个子组中的数据样本量，xcij，xij和yij分别为第i个子组中第j（j ＝1，2，…，ni）个混杂变量、自变量和因变量的数值。

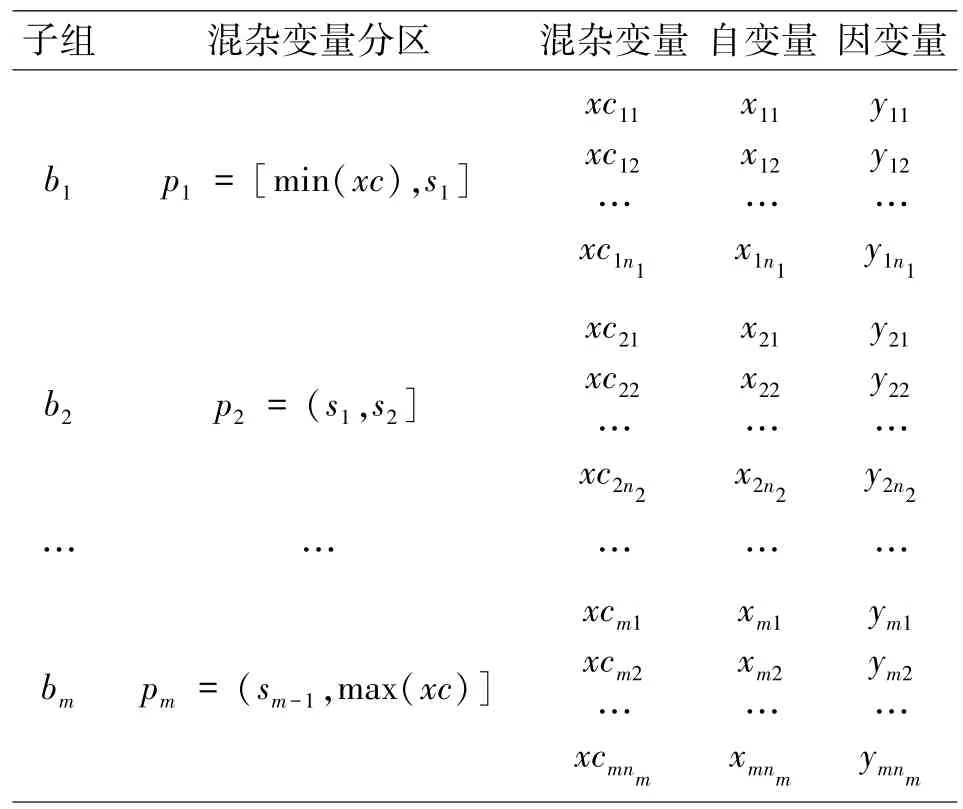
表1 根据混杂变量分组后的数据统计表

分组时需要考虑两个方面的平衡：第一，每个子组都应该具有尽可能好的“同质性”，即各子组中的数据彼此之间比其他子组中的数据更“相似”。第二，有数量适当的数据点，数量过少的子组会缺乏显著性，而数量过多的子组对于稳健趋势判断来说可能太不均匀。分组的目标是期望“组内差异最小化，各组之间差异最大化”，最大限度地在子组内剔除混杂变量的干扰。

3.1.2 差异分组

采用差异分组法对汇总数据进行分组，通过在混杂变量上寻找最佳分割点s，将汇总数据分割成两个满足组间差异最大化、组内差异最小化要求的分区，通过递次迭代的方法，进一步寻找两个分区的最佳分割点对分区进行分组，逐步将原来的汇总数据分割成满足需要的子组集合。

衡量差异需要区分“组间差异” 和“组内差异”，此时可以引入总偏差平方和TSS（Total Sum of Square）来描述因变量y的差异变化，其计算公式为：

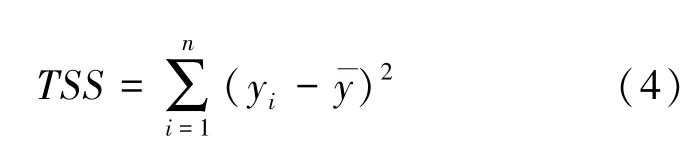
式（4）中，yi是因变量y的第i个数据值，是所有因变量y数据值的平均值。

对于混杂变量xc，可以通过拆分总平方和来量化因变量y的差异变化，总平方和＝组间平方和+组内平方和。即：

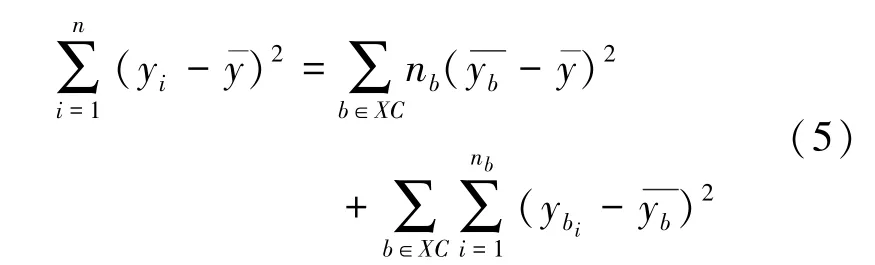
式（5）中，b是汇总数据根据混杂变量分解后的子组，nb是子组b中的数据点数量，ybi是子组b中的第i个数据点，是该子组中数据值的平均值。

为了衡量组间数据差异性大小，可以定义一个组间差异系数R。组间差异系数R是分组平方和与总平方和的比例，R的大小反映了组间数据差异性的大小。

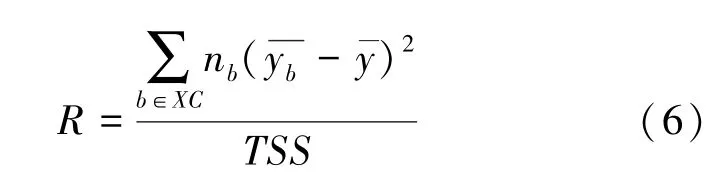
对于混杂变量xc，R取值在0～1 之间，R越大表示组间差异越大，同时组内差异越小。

对于表2 所示的汇总数据，混杂变量xc的域可以由其中某个值s分成两个分区p1和p2：［min（xc），s］ 和（s，max（xc）］，同时对应的汇总数据可以分成子组b1和b2，其组间差异系数为：

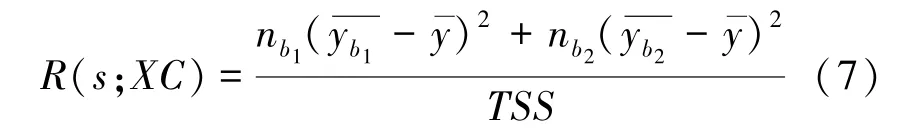
简化可得：

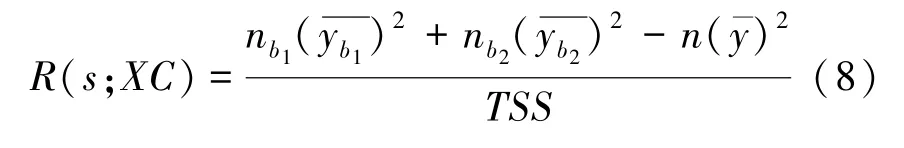
式（7）中，nb1是子组b1中数据点的数量，nb2是子组b2中数据点的数量。由此，在s的所有可能值中，可以选择最大化R的值s0作为混杂变量域的最佳分割点。对于分组后的子组b1，b2，采用同样的分解方法，进一步选择最佳分割点s1，s2来迭代分解数据。通过这种迭代，分割混杂变量的值域，形成m个子组。理论上这个过程可以持续进行下去，直到混杂变量被分割成由单个点组成的子组。

3.1.3 避免过度分割

为了防止过度分割，可以进行某种约束，例如，设定子组中数据点一旦小于某个设定值w就不再进行分割。为方便数据统计与计算，可设定：

若数据总量n≥1000 时，；否则w＝10。

3.2 趋势拟合

为对比数据在汇总中和分组中的趋势，采用线性模型来量化x与y之间的关系。线性模型计算上较为简单，在数据量不大的情况下，工程上误差可以接受。最小二乘法基本的线性回归方法如下。

将自变量x与因变量y的数值对应的n个点记作（xi，yi），i ＝1，2，…，n，待确定的直线方程记作y ＝α+βx，误差记作E。由此：

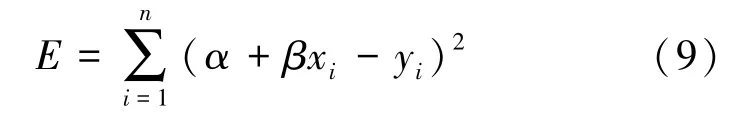
根据拟合出的直线的斜率β的正负值，判断因变量y随自变量x是递增趋势或递减趋势。为便于对比，我们采用符号函数sgn 来量化β的正负值，即β ＝0 时，sgn（β）＝0；β ＞0 时，sgn（β）＝1；β ＜0 时，sgn（β）＝-1。

3.3 趋势对比

趋势对比就是将各子组中的变量变化趋势分别与汇总情况下趋势进行对比。将sgn（β1），sgn（β2），…，sgn（βt）分别与sgn（β）进行比对，不同子组的个数记为v，若v≥m／2，则视为子组内趋势与汇总时趋势不同，判断其为存在悖论。

3.4 趋势对比检测法算法流程

趋势对比检测法（TCD）算法流程示意图如图2 所示，步骤如下。

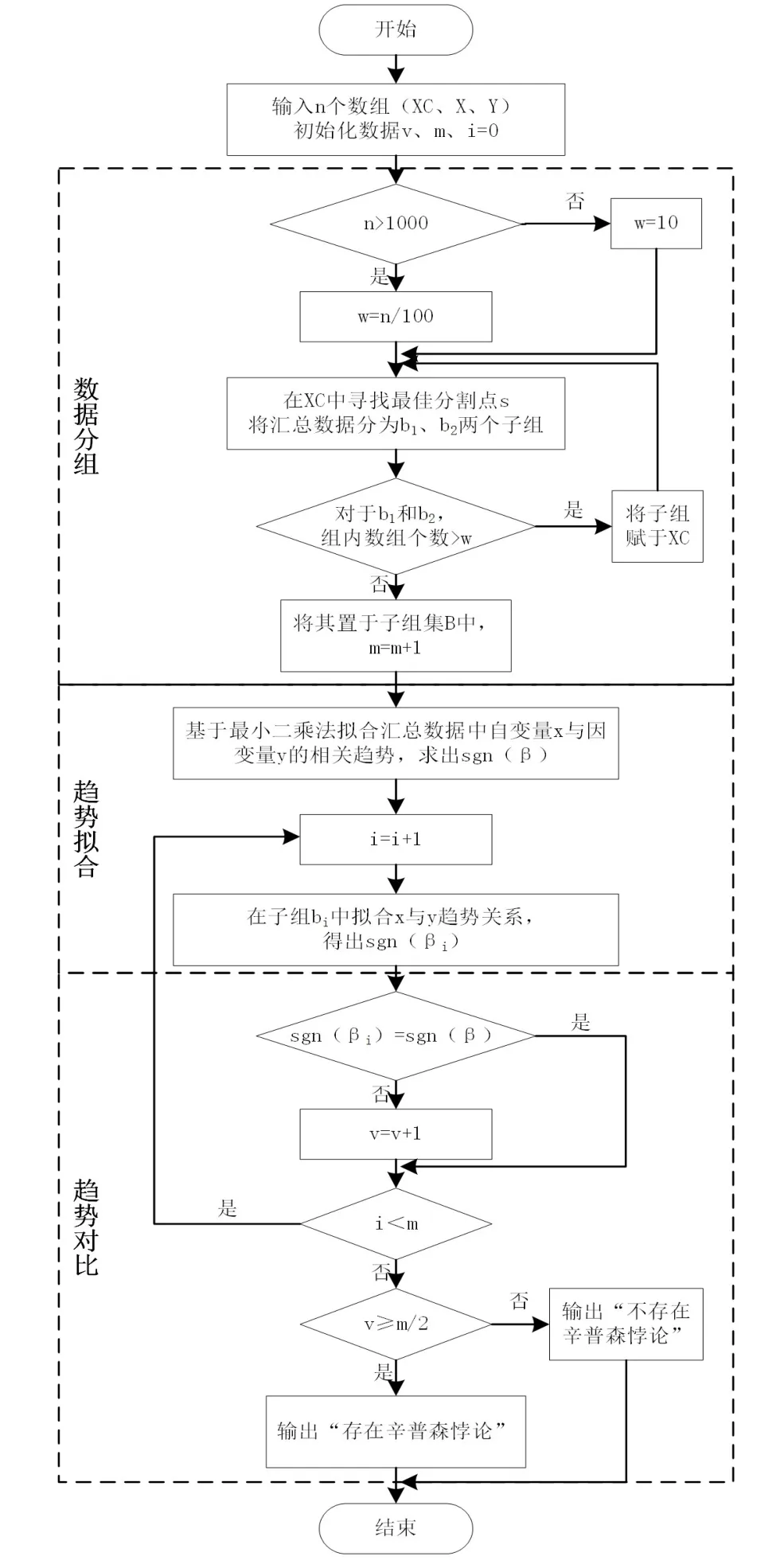
图2 趋势对比检测法算法流程示意图

步骤1：输入数据，n个数组，包含混杂变量xc、自变量x和因变量y。

步骤2：在混杂变量上通过差异分组法进行数据分组。将汇总数据共分成m个子组。

步骤3：基于最小二乘法拟合汇总数据中因变量y随自变量x变化的相关趋势，得出斜率β，进而得出sgn（β）。

步骤4：基于最小二乘法拟合各子组中y与x的关系，得出斜率β1，β2，…，βm的值，求出sgn（β1），sgn（β2），…，sgn（βm）。

步骤5：进行趋势对比，判断是否存在悖论。

4 示例检验

分析部队兵龄层次与实弹射击成绩之间的关系。将兵龄由短到长分为1～3 档，射击环境能见度由低到高赋值0～4，射击成绩满分为100 分，数据见表2。简单统计似乎新兵比老兵成绩好。然而由于数据采集时环境能见度不同，需要检测能见度是否对分析结果造成影响。

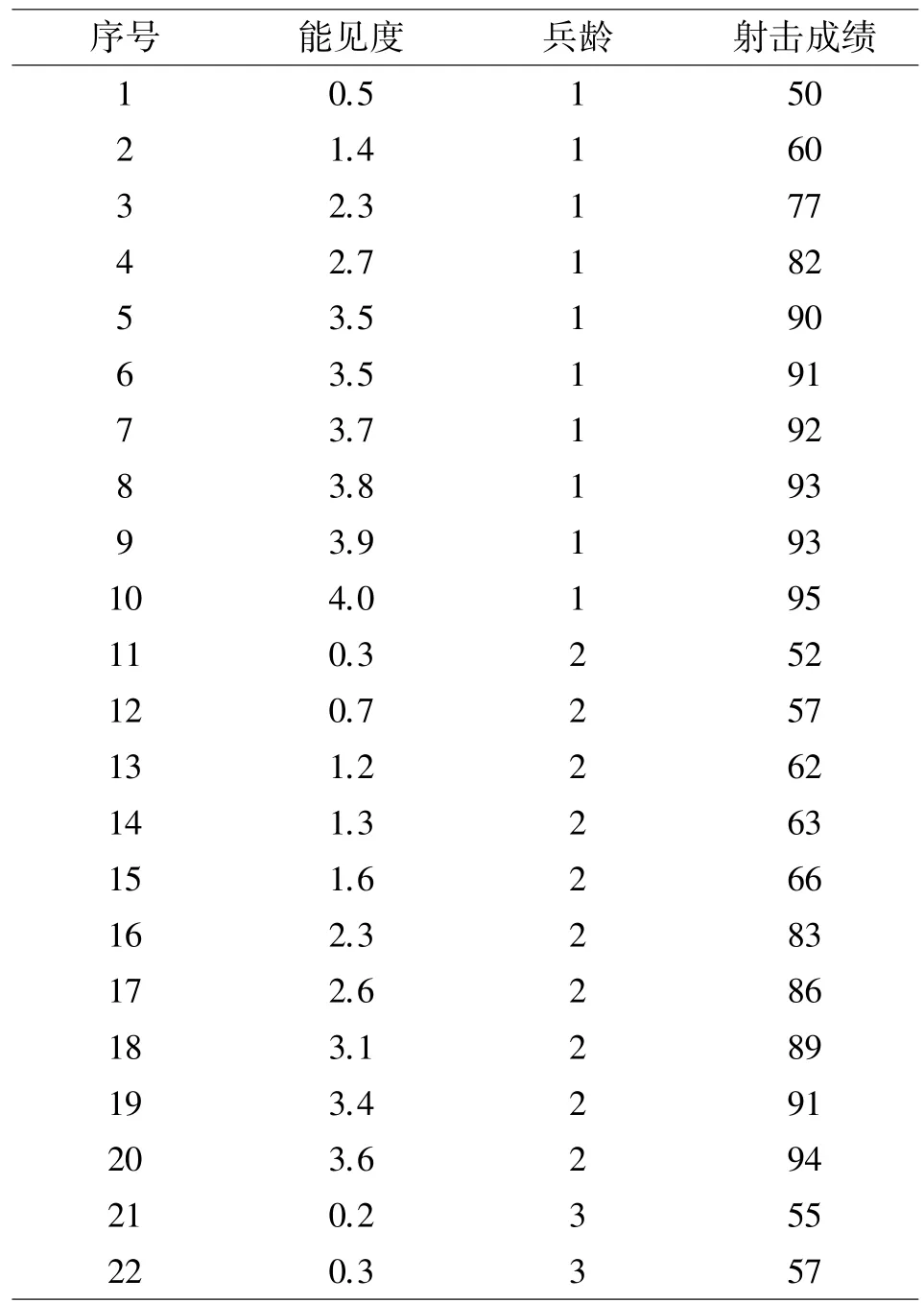
表2 不同兵龄层次射击成绩统计表

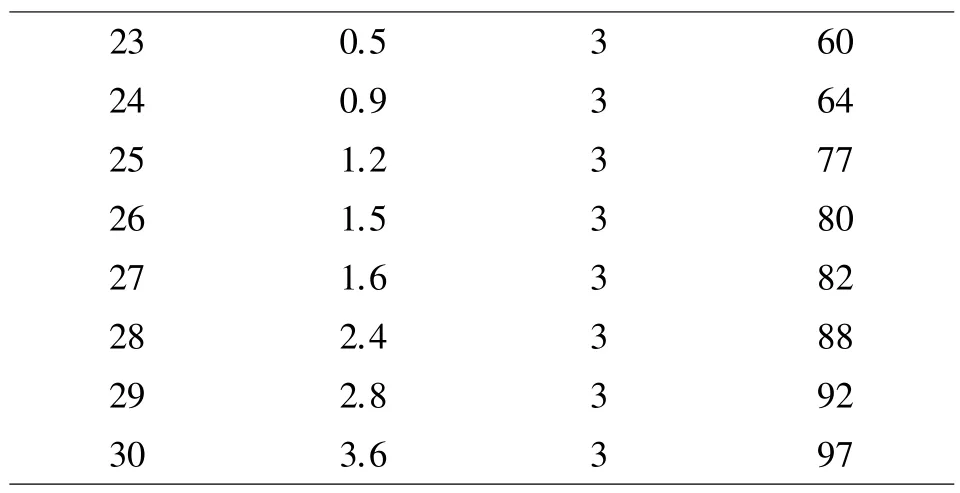
续表2

步骤1：输入数据，n ＝30，兵龄层次数值即为自变量x，射击成绩即为因变量y，能见度为混杂变量xc。

步骤2：通过划分能见度的区间来分解数据。运用差异分组法将混杂变量的域分成4 个分区，pxc1＝［0.2，0.9］，pxc2＝（0.9，1.6］，pxc3＝（1.6，2.7］，pxc4＝（2.7，4］，然后将汇总数据按照混杂变量分区分成4 个子组。

步骤3：拟合汇总数据中射击成绩随兵龄变化趋势。基于最小二乘法拟合得到线性方程为：y ＝-3.45x +84.233，其中β ＝-3.45＜0，sgn（β）＝ -1。

如图3 所示，汇总数据中射击成绩随兵龄增长而降低，呈递减趋势。

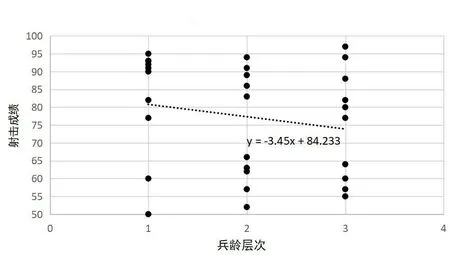
图3 汇总数据中兵龄层次与射击成绩关系示意图

步骤4：在各子组中线性拟合x与y的关系，得到方程如下。

子组1：xc∈［0.2，0.9］时，线性方程为y1＝4.5x1+45.5，其中β1＞0，sgn（β1）＝1；

子组2：xc∈（0.9，1.6］时，线性方程为y2＝11.375x2+44，其中β2＞0，sgn（β2）＝1；

子组3：xc∈（1.6，2.7］时，线性方程为y3＝4.357x3+75.357，其中β3＞0，sgn（β3）＝1；

子组4：x c∈（2.7，4］时，线性方程为y4＝1.153x4+90.75，其中β4＞0，sgn（β4）＝1。

各子组趋势图如图4 所示。

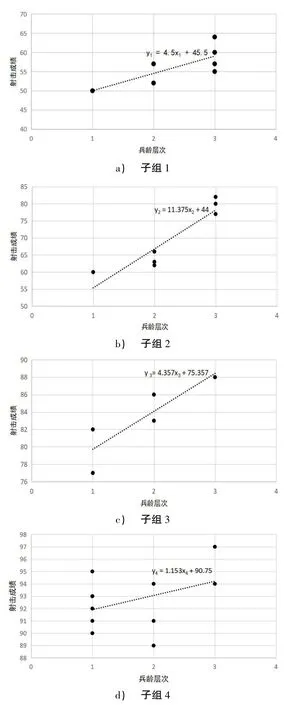
图4 不同子组中兵龄层次与射击成绩关系示意图

步骤5：对比图4 中不同子组所拟合出的直线和图3 中汇总数据所拟合出的直线的变化趋势，即将sgn（β1），sgn（β2），sgn（β3），sgn（β4）分别与sgn（β）进行对比，发现在汇总数据中，因变量y随自变量x增加呈递减趋势，而在各子组数据中均呈递增趋势。由此表明，汇总数据的自变量和因变量的变化趋势在子组中均被逆转，这表明混杂变量能见度对研究兵龄层次与射击成绩相关性时存在干扰，判定此数据统计分析存在辛普森悖论。在这一组数据中，如果采用不同的统计方式分析数据，就会出现不一致的结论。

5 避免辛普森悖论的几点建议

随着基于数据的研究和决策日益增多，军事领域评估对象日趋复杂，多指标综合评估时容易忽略隐形混杂变量，为避免出现辛普森悖论，提出三点建议。

5.1 数据搜集时充分考虑环境类别覆盖面

在军事评估数据采集时，需要选择熟悉业务的人员参与，以专业的眼光确定评估对象需要的样本数量和环境的多样性。面对不同的对象、不同的应用背景，会有不同的侧重，这就需要充分考虑所处的背景环境。在原始数据采集中，环境变量的类别要记录得足够充分，确保环境类别的覆盖面充分。

5.2 数据分析时要注意均衡变量影响

在定量分析阶段，需要时刻考虑每一个因素的权重，考虑各因素随环境条件变化而受到的不同影响，不应该简单地数量相加。在多指标评价体系中，由于各评价指标的性质不同，通常具有不同的量纲和数量级。当各指标间的影响水平相差很大时，如果直接用原始指标值进行分析，就会突出数值较高的指标在综合分析中的作用，相对削弱数值水平较低指标的作用，导致辛普森悖论的出现。因此，为了保证结果的可靠性，要尽可能地对原始指标数据进行标准化处理，以均衡各指标变量对最终结果的影响。

5.3 综合评估时要考虑过程性影响

在分层级的评估中，混杂变量的影响可能会由下层向上层传导。例如一项选拔由体检和后续考核组成，如果体检采取一票否决制，先检查身高再检查视力，和先检查视力再检查身高相比，所筛选出的对象可能会不同。在第一轮考核合格的基础上进行下一轮考核，其数据就不能有效反映第一轮体检中混杂变量的影响。在样本差异较大的情况下，这一问题会非常突出。因此在对数据进行综合分析评判时，特别需要考虑评价程序对结果的影响。

6 结束语

本文通过对数据统计中的辛普森悖论的分析，提出了趋势对比检测法，用于检测数据中的混杂变量导致的结论偏差。文中提出的趋势对比检测法适用于单个混杂变量，尚不能检测多个混杂变量，多混杂变量影响检测是下一步要研究的问题。