单元整合梳理脉络 构建体系揭示本质——以“分数的基本性质”教学为例

西南大学附属小学（400700） 代 阳 潘 怡

分数是小学数学“数与代数”课程内容的难点，具有高度抽象性、意义丰富性、内涵多样性、运用广泛性的特点。“分数的基本性质”是学生学习约分、通分、大小比较及分数四则运算的重要基础，不但在单元教学中具有承前启后的作用，而且对学生的后续发展有重要影响。对此，笔者从现代教学观的整体教学设计理念出发，通过对单元内容的整体分析与重构，立足于学生认知发展水平和对数学本质的有效揭示，进行资源的开发、利用、重构及整体设计，实践了单元整体视域下的课堂教学设计。

一、单元视角下的分数知识梳理

1.研读课程标准

课程标准关于分数的教学目标提出了“体验从具体情境中抽象出数的过程，理解分数的意义。初步形成数感和空间观念，感受符号和几何直观的作用”“结合具体情境理解小数和分数的意义”“会进行小数和分数的转化”“能比较分数的大小”“能解决小数、分数的简单实际问题”等要求。

基于课程标准的启示，教师在教学时应注意：（1）让学生经历具体到抽象的学习过程，尽可能地利用学生的生活经验，运用各种直观因素，让学生借助充分的感性材料，发现和归结一类事物的一般和本质特征，从而建构抽象的数学概念。（2）揭示知识之间的内在联系，沟通相关知识与方法的联系，使学生在理解的基础上掌握数学方法与概念。

2.单元分析解构

基于对课程标准的分析，笔者团队对西师版教材中分数单元的内容进行了拆解与重构。在西师版教材中，分数单元共6个部分，11个课时（见表1）。

表1 西师版教材五年级下册分数单元教学内容

从单元整体教学设计的角度来剖析，本单元的内容主要分为分数的意义和分数的基本性质。

（1）从分数的意义出发，可以分数单位为生长点，从真分数迁移到假分数，再基于分数意义中分数与除法的关系，引导学生理解分数与小数的互相转化。（2）将分数的基本性质与除法商不变的规律建立联系，并引导学生对分数的基本性质进行运用，包括约分、通分、分数的大小比较。由此对单元内容进行重新整理设计，重新整合后的分数单元共三大部分，13个课时（见表2）。

表2 重新设计的分数单元内容

二、“分数的基本性质”课堂教学案例

1.以学定教，确定教学目标

笔者根据重新设计的单元课时进行了“分数的基本性质”课堂教学。在知识结构方面，学生已经学习了分数的意义、分数与除法的关系、商不变的规律等知识，这些知识经验就是学生学习本节课的逻辑起点；在素养能力方面，学生已具备初步的抽象概括能力，但仍需依托直观形象与感性经验，并联系直接经验以形成抽象逻辑思维。

为了更好地把握学生的认知起点，笔者在课前对学生进行了测试。测试后发现：绝大部分学生能够感悟并运用分数的基本性质来判断两个分数是否相等，但对分数的基本性质的认识处于模糊、泛化的层次；一半左右的学生可以用自己的方法证明与相等，对商不变的性质和分数的基本性质之间的关系也有初步的感知，但不能从本质上来理解分数的基本性质。

根据前测结果，结合课程标准，笔者重点靶向学生数学抽象、逻辑推理和几何直观素养的培养，制订如下教学目标：（1）经历探索分数的基本性质的过程，理解分数的基本性质；（2）能运用分数的基本性质解决简单的实际问题；（3）体会变与不变的辩证关系，培养观察、比较、抽象、概括、迁移的逻辑思维能力；（4）经历猜想、验证、实践等数学活动，体验数学学习的乐趣。

2.情境引入，提出猜想验证

生1：4 个分数的大小相等，因为4 张海报的图画部分都占小报的一半。

师：那它们的分子和分母有什么变化？

生2：从左往右看，分子和分母同时乘一个相同的数，分数大小不变；从右往左看，分子和分母同时除以一个相同的数，分数大小不变。

生3：这4 个分数的分子和分母同时乘或除以一个相同的数，分数的大小不变。

师：是不是所有的分数都有这样的规律呢？下面我们来验证一下。

新课引入时，运用贴近学生生活的素材，引导学生多角度观察，找出分数分子和分母的变化规律，通过合情推理初步概括出分数的基本性质。

3.举例验证，完善性质内容

师：该如何验证？

生5：还应注意，分子与分母同时乘以或除以的数不能是0，因为分母不得为0。

师（小结）：分数的分子和分母同时乘以或除以一个相同的数（0 除外），分数的大小不变。这就是分数的基本性质。

本环节旨在让学生运用不完全归纳法来验证猜想。学生通过多种验证方法，结合分数与除法的关系、商不变性质等旧知来验证。在验证的过程中，学生形成了观察、比较和迁移的逻辑思维能力。

4.沟通联系，揭示性质本质

师：提到性质，我们还学过什么的性质？回想一下并填空，说说你有什么发现（如图1）。

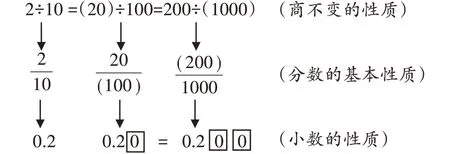
图1 运用三种性质填空

生1：我们之前还学过小数的性质、商不变的性质，这几种性质之间可以相互转化。

师（出示图2）：为什么分数和小数会有这样的性质？观察图2 中的0.3 和0.30，说说你有什么发现。

图2 0.3与0.30的计数单位示意图

生2：0.3 表示3 个0.1，0.30 表示30 个0.01，从0.3 到0.30，计数单位在缩小，计数单位的个数在增多。

生3：从0.1 到0.01，计数单位缩小到原来的十分之一，也就是除以10；从3 个到30 个，计数单位的个数扩大到原来的10 倍，也就是乘10。相互抵消，所以0.3=0.30。

图3 的分数单位示意图

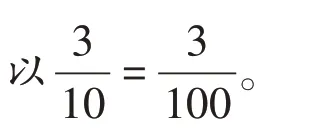
本环节通过沟通分数的基本性质、小数的性质和商不变的性质，建构起知识间的脉络和体系。借助直观图形，先从小数的性质入手，再将其迁移到分数，引导学生从分数单位的大小与分数单位的个数的关系来感悟分数的基本性质，达到让学生知其然，更知其所以然的教学目的。

5.借助数轴，拓展延伸数系

师（出示图4）：观察图4并思考，对于数轴上的某个点，为什么用分数或小数来表达就可以有多种形式，而整数就做不到呢？这个问题留给大家课后思考。

图4 根据数轴拓展数域

本环节体现了“等价”思想，在串联整数、小数、分数的同时，向学生提出整数为什么不具备此类性质的问题，供学生探究和反思。

三、单元设计下的课堂教学反思

1.双线并进，聚焦数学素养

2.把握逻辑，打造知识体系

在教学时，教师应从知识的整体出发，着眼于如何整体推进教学，构建完整的知识体系，更好地展现数学知识的有序性和完整性，让学生感知知识间的联系，并逐步完善知识体系。在本课的教学中，教师从学生的已知出发，将学生已学的小数的性质、商不变的性质进行串联，以数形结合的方式从分数单位的大小及个数的角度来理解分数的基本性质，凸显了数学的本质。