LSTM神经网络和量纲分析法在弧形闸门过流计算中的对比

2022-11-15王艺霖靳燕国陈晓楠段春青张召雷晓辉常文娟

南水北调与水利科技 2022年3期

王艺霖,靳燕国,陈晓楠,段春青,张召,雷晓辉,常文娟

(1.中国水利水电科学研究院流域水循环模拟与调控国家重点实验室，北京 100038；2.南水北调中线干线工程建设管理局，北京 100038；3.北京市水务局政务服务中心，北京 100071)

节制闸是明渠调水工程的一种重要控制建筑物，其通过调节闸门开启度来控制渠道的水位和流量[1]，闸门的安全性能和使用性能一直备受关注[2]。其中，弧形闸门因其具有重量轻、启门力小、过闸水流流态更稳定、操作和维护简单等优点[3]，在各大明渠调水工程中得到了广泛应用。过闸流量的精确计算对于工程建筑物的设计和运用、渠道的水力控制、输水系统水力特性分析等均具有重要意义。

基于能量方程，目前已存在较多的弧形闸门过流经验公式，常见的有武水公式[4-5]、南科院公式[6]、清华大学公式[7]、Henry公式[8]等。以上经验公式虽已得到较为广泛的应用，但在适用条件和参数率定方面仍然存在一定局限性。由于弧形闸门结构相对复杂，经验公式中流量系数、淹没系数等参数的率定自身已具有一定的难度，加之该系数随水流状态的变化而变化，故流态切换时个别经验公式将不再适用。另外，经验公式的闸门流量系数多为闸门开度及上、下游水头差的函数，且关系式大多为非线性关系，率定过程中涉及一系列迭代问题，使得参数率定过程繁冗复杂而误差较大。鉴于经验过流公式存在的诸多问题，近些年又提出了基于量纲分析的过流计算方法，较多专家学者将两者进行了对比。郭永鑫等[9]针对闸孔出流的不同流态，分别建立了经验系数模型和量纲分析模型，结果表明不同流态下量纲分析模型流量计算误差比经验系数模型低5%左右。崔巍等[10]基于常规弧形闸门过流公式，进一步推导了基于量纲分析的弧形闸门无量纲关系式，并得到无量纲闸门参数相对于常规过流公式参数率定误差减小约10%的结论。Metzler[11]、Toch[12]和Bijankhan等[13]采用传统能量公式和量纲分析法分别率定了过闸流量与闸门开度、闸前水深、闸后水深等各因素之间的关系，评估了不同方法对于闸门水力计算的影响效果，发现量纲分析法具有参数率定过程相对简易、计算精度较高的特点。刘孟凯等[14]通过弧形闸门水槽试验，对比分析了基于能量方程和量纲分析的流量计算公式，结果表明了传统闸门水力计算公式的计算精度比率定后的量纲分析公式稍差，且率定工作更为复杂。由此可见，量纲分析法能够有效避免经验公式的一些缺点，故此本文选用量纲分析法构建弧形闸门过流计算模型。

近年来，大数据、人工智能等新一代信息技术的快速发展引领了众多行业的技术变革，机器学习、深度学习、强化学习等通过数据驱动的先进技术方法逐渐受到了学者的青睐。其中，长短期记忆网络作为一种特殊的循环神经网络，具有较为强大的时间序列处理能力，可以选择性地保留前面若干时刻的信息，能够满足时间序列动态预测的要求[15]，该方法已在股票预测[16-17]、网络安全[18]、语义识别[19]等行业得到了广泛应用，而在水利行业，尤其是长距离调水工程中则应用较少。由于闸门流量与闸门开度、上下游水深等要素之间具有较强的相关性[20]，基于此，本文构建长短期记忆神经网络模型，充分发挥该方法的优势，通过长序列历史数据得到与闸门流量间的映射关系，并对其进行实时计算。

南水北调中线工程自通水以来，已积累了长序列历史水情数据，数据量充分满足模型构建需求。因此，以中线工程为研究对象，在常规闸门流量公式基础上，从机理和数据两个不同层面提出了改进的流量计算方法，并通过对比分析得到不同方法下南水北调中线工程弧形闸门流量计算的误差效果及适用条件，为该工程的水力计算及调度运行提供科学依据。

1 模型方法

弧形闸门水力结构见图1。

对于经验公式，流量计算表示为

(1)

式中：Q为过闸流量，m3/s；σ为淹没系数；M为闸门综合流量系数；B为过水断面宽度，m；e为闸门开度，m；g为重力加速度，m/s2；H0为闸前水深，m。

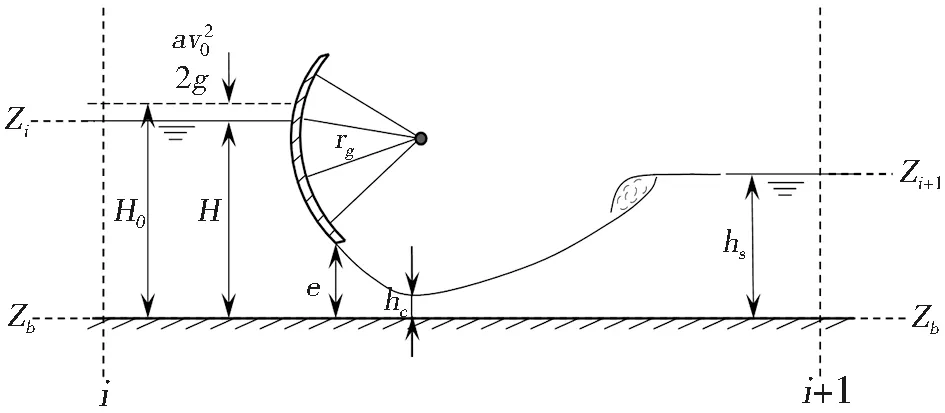
图1 弧形闸门Fig.1 Arc gate

1.1 量纲分析法

由于受闸门型式、渠道结构布置、上下游水流条件等因素的影响，经验公式更多适合于闸孔自由出流条件下的流量计算，对于淹没出流则不太通用[21]。基于此，Chadwick等[22]首次采用量纲分析的方法对闸门过流特性进行计算，对于弧形闸门，在淹没流情况下，单宽流量q是闸门开度e、重力加速度g、过闸前后能量差HE和绝对黏性系数μ的函数，其函数关系为

q=f(e,g,HE,μ)

(2)

式中：HE=E0-H2；H0表示闸门上游水深，m；H2表示闸门下游水深，m。若流态为自由出流，则H2=0。

假定过闸流量具有如下形式，其中a、b、c、d和m为常数系数。

(3)

通过量纲分析可转化为

(q2/g)1/3=m2/3e(HE/e)2c/3

(4)

化简得到

K/e=i(HE/e)j

(5)

式中：K=(q2/g)1/3，i=m2/3，j=2c/3。

通过等式变换，按照常规闸门过流公式的形式，推导出基于量纲分析法的弧形闸门过流公式为

(6)

为了便于闸门系数的率定，对公式(5)等式两边取对数，可转化为lg(HE/e)与lg(K/e)之间的线性关系为

lg(K/e)=lgi+jlg(HE/e)

(7)

令y=lg(K/e)，x=lg(HE/e)，a=j，b=lgi，则式(7)简化为线性方程

y=ax+b

(8)

可以看出，系数率定最终转化为简单线性关系式中斜率和截距的拟合，相较于常规弧形闸门过流公式的系数率定，该方法更加简便。

1.2 长短期记忆(LSTM)神经网络

LSTM最早由Hochreiter等[23]提出，是一种特殊的递归神经网络(recurrent neural networks，简称RNN)变体[24]，与其具有相似的循环结构，见图2。

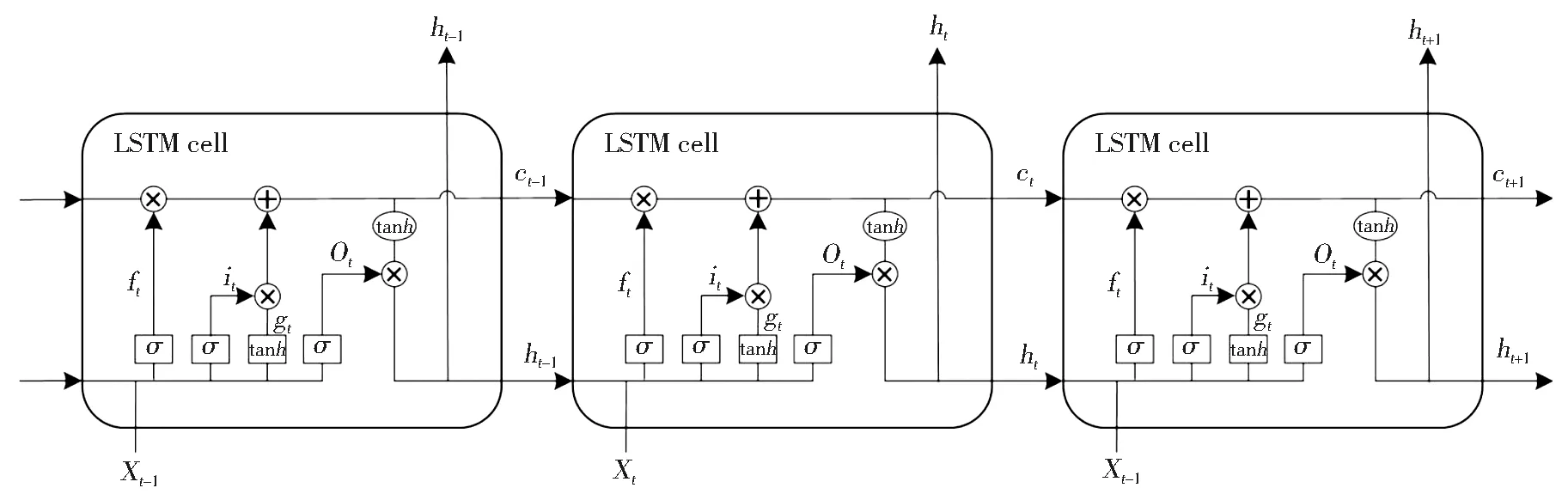
图2 LSTM单元结构Fig.2 Cell structure of LSTM

相比普通的RNN，LSTM在隐含层各神经元中增加了“记忆块”，将反向传播中的累积转化为累加，削弱了过程中梯度消失或梯度爆炸的问题，具有较好的记忆信息控制[25-26]。其门控结构原理如下。

遗忘门(forget gate)：输入上一时间序列的隐藏状态和当前时间序列输入信息，得到遗忘门输出信息，公式为

fi=σ(Wfht-1+Ufxt+bf)

(9)

输入门(input gate)：ht-1和xt经过sigmoid层和tanh层得到it和gt，这两个变量传递所需的新信息从而更新细胞记忆，公式为

it=σ(Wiht-1+Uixt+bi)

(10)

gt=tanh(Wcht-1+Ucxt+bc)

(11)

Ct=Ct-1⊙ft+it⊙gt

(12)

输出门(output gate)：ht-1和xt首先经过Sigmoid层得到细胞状态的输出部分,其次经过tanh层进行数据处理，得到更新后细胞状态ht，公式为

ot=σ(Woht-1+Uoxt+bo)

(13)

ht=ot⊙tanh(Ct)

(14)

式(9)～(14)中：Wf、Wi、Wo分别表示从遗忘门、输入门、输出门到输入的权重矩阵；Uf、Ui、Uo分别表示从遗忘门、输入门、输出门到隐藏层的权重矩阵；bf、bi、bo分别表示遗忘门、输入门、输出门的偏置向量；gt表示tanh层输出；⊙表示矩阵元素积。

由于闸门过流计算具有较强的非线性，可基于南水北调中线工程长序列历史水情数据，构建LSTM模型以描述弧形闸门水流过闸时的非线性关系，从而直接或间接得到过闸流量的时间序列。LSTM模型包括了训练、验证和测试3个阶段。经过数据归一化处理后，为保持独立同分布的特性，将数据按7∶2∶1顺序划分为训练集、验证集、测试集。由于闸门流量公式中，过闸流量与闸前水位、闸后水位、闸门开度具有较强的相关性，其间的具体函数关系无须推求，可直接用黑箱模型代替，故以0时刻至t时刻的闸门开度、1时刻至t+1时刻的闸前水位、闸后水位以及过闸流量作为模型输入，该输入是一个4×t的二维矩阵。二维矩阵输入到模型后：首先经过一层输出维度为32的LSTM层，得到4×32的二维中间变量；其次经过输出维度为64的LSTM层，得到4×64的二维中间变量，将其展平为256的一维变量；最后经过全连接层得到模型流量计算结果，即模型输出。可以看出，该方法进行闸门流量计算时，无须进行参数率定，可直接辨识出闸门流量与其他过流特性之间的映射关系。且该方法具有较强的自适应特点，可随着数据的更新，自适应调整模型参数，避免了不断进行参数率定的不便，极大程度减轻了流量计算的工作量，提高了可靠性。

2 基于机理及数据的过闸流量计算

由于南水北调中线工程首末两端闸门分别连接上游水库、下游泵站等非渠道建筑物，其过流特性相较于工程中其余闸门会受到一定程度的影响，因此为控制环境变量，仅以工程总干渠中间59座节制闸为研究对象。经对历史数据分析，中线工程闸门处的流态多为淹没处理，故剔除其中自由出流数据，选取2018年1月至2019年12月共2年2 h时间尺度的实测数据作为模型输入，采用量纲分析法和LSTM神经网络2种方法对各闸门进行过闸流量计算，从中线工程的角度对比分析2种方法的计算效果及适用情况。

2.1 量纲分析闸门参数率定

以lg(HE/e)为横轴，lg(K/e)为纵轴，绘制历史数据点并进行线性拟合。限于文章篇幅，仅以磁河倒虹吸出口节制闸(50号)、沙河(北)倒虹吸出口节制闸(51号)、漠道沟倒虹吸出口节制闸(52号)3个节制闸为例，展示闸门过流系数拟合曲线结果见图3。

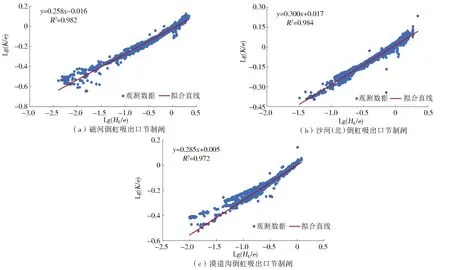
图3 3个节制闸量纲分析闸门过流系数率定结果Fig.3 Calibration results of overflow coefficient of dimensional analysis method for 3 control gates

通过曲线拟合公式计算得到中线59座节制闸闸门过流系数率定结果统计见表1。

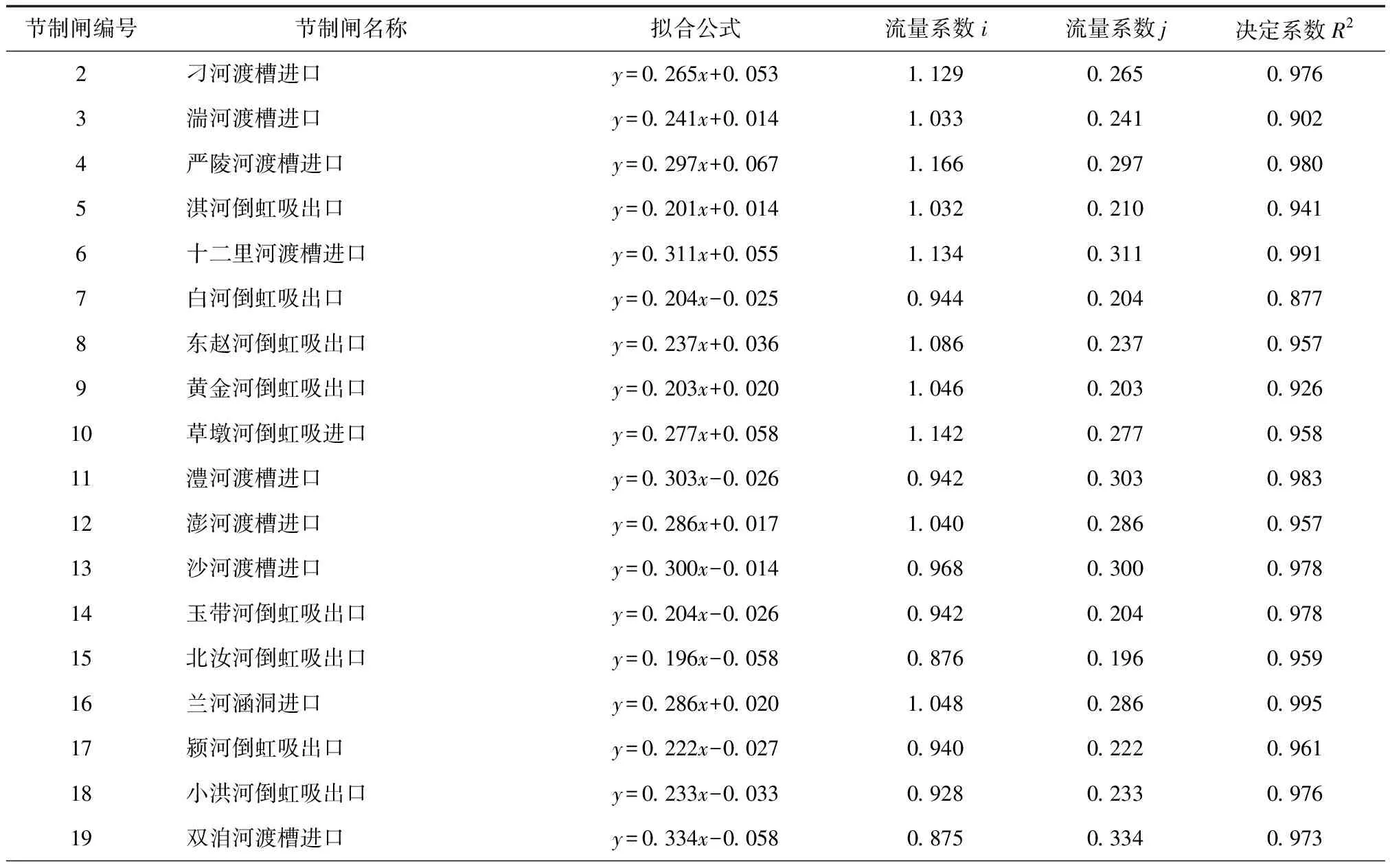
表1 中线干渠59座节制闸闸门无量纲过流系数率定结果Tab.1 Calibration results of overflow coefficient of dimensional analysis method for 59 control gates in the Middle Route of South-to-North Water Transfers Project

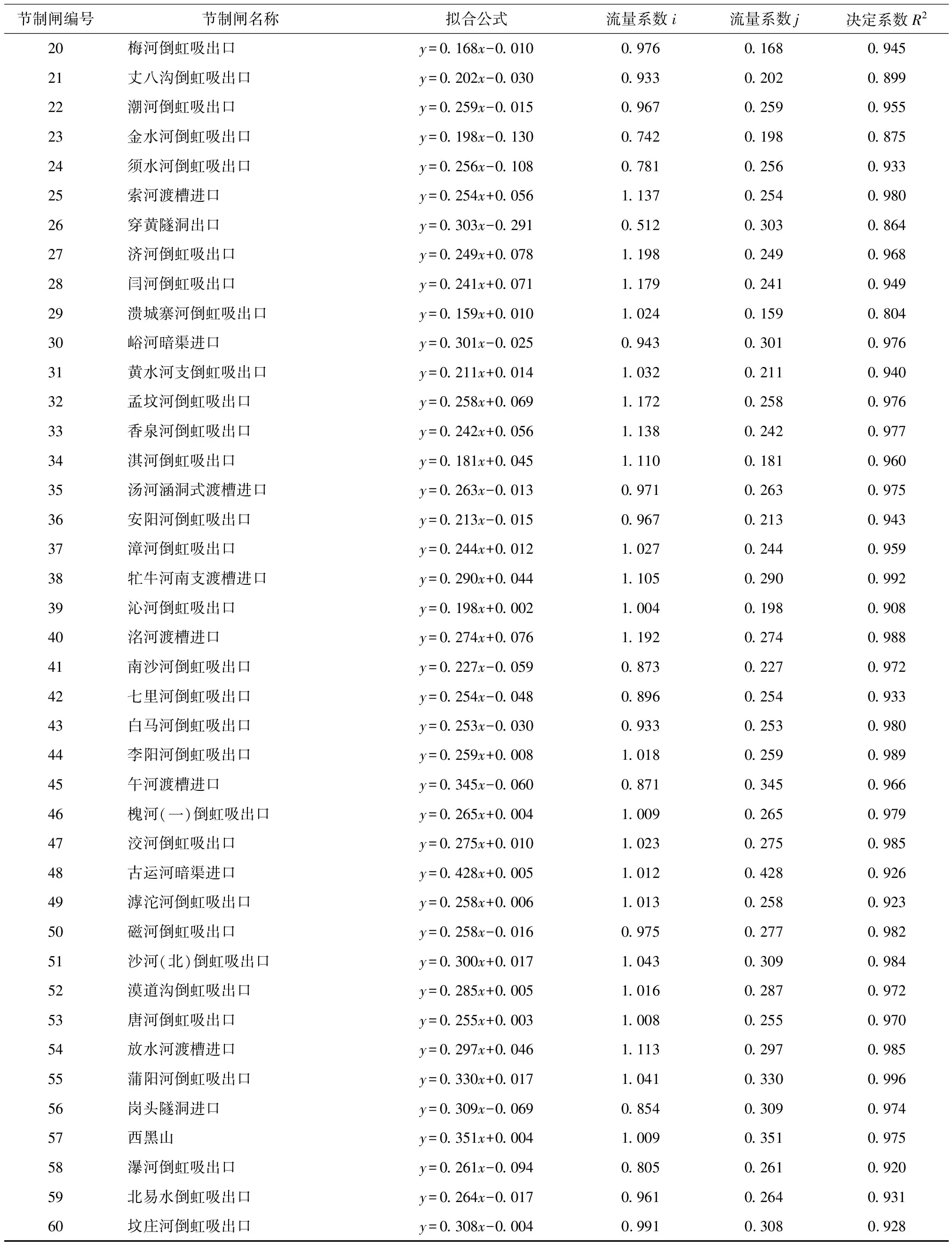
表1(续)Tab.1 (Continued)

通过以上参数率定结果可以看出，lg(K/e)与lg(HE/e)呈较好的正向线性关系，拟合曲线与实测数据吻合较好，大部分节制闸的确定性系数R2大于0.95，表明量纲分析闸门过流系数率定结果较为可靠。

从表1可进一步发现：峪河节制闸以北，各节制闸闸门过流系数率定结果均在0.9以上，结果较好；峪河节制闸以南，部分节制闸(如：溃城寨河倒虹吸出口节制闸(29号)、穿黄隧洞出口节制闸(26号)、金水河倒虹吸出口节制闸(23号)、白河倒虹吸出口节制闸(7号))的确定系数R2低于0.9，拟合结果相对其他节制闸较差。经分析，以上4个闸门参数率定结果较差的可能原因如下。

对于穿黄隧洞出口节制闸(26号)，该节制闸连接中线工程直径最大的穿黄隧洞，由于隧洞输水过程对压强、温度等外界影响较为敏感，出口处水位波动较大，数据集相对离散。

对于溃城寨河倒虹吸出口节制闸(29号)、金水河倒虹吸出口节制闸(23号)、白河倒虹吸出口节制闸(7号)，观察用于参数率定的原始数据，发现自变量和因变量间的线性关系并不明显，估计为检测设备系统偏差导致，加之此处存在较多闸门检修情况，破坏了数据的一致性。

综上结果表明,中、下游参数率定结果整体优于上游，因此该方法更适用于中、小流量情况下的闸门过流系数拟合。

2.2 弧形闸门流量计算

选取2019年4月整月2 h时间间隔的实测闸前水位、闸后水位及闸门开度等数据，利用参数率定后的量纲分析模型、训练后的LSTM模型进行闸门流量计算，并采用平均绝对误差、平均相对误差、均方根误差3个指标进行比较，结果见图4至图6。

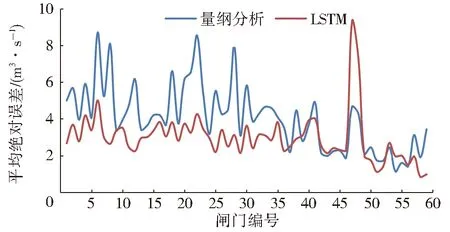
图4 流量平均绝对误差对比Fig.4 Comparison of average absolute error of discharge

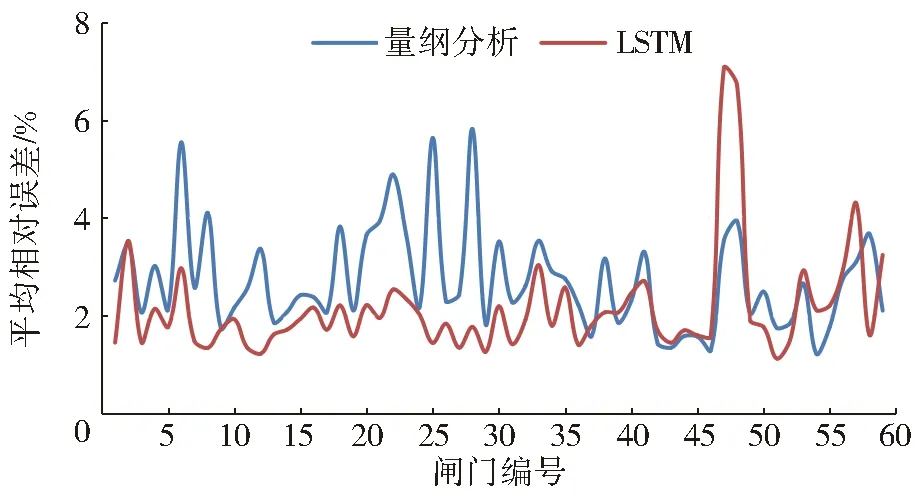
图5 流量平均相对误差对比Fig.5 Comparison of average relative error of discharge

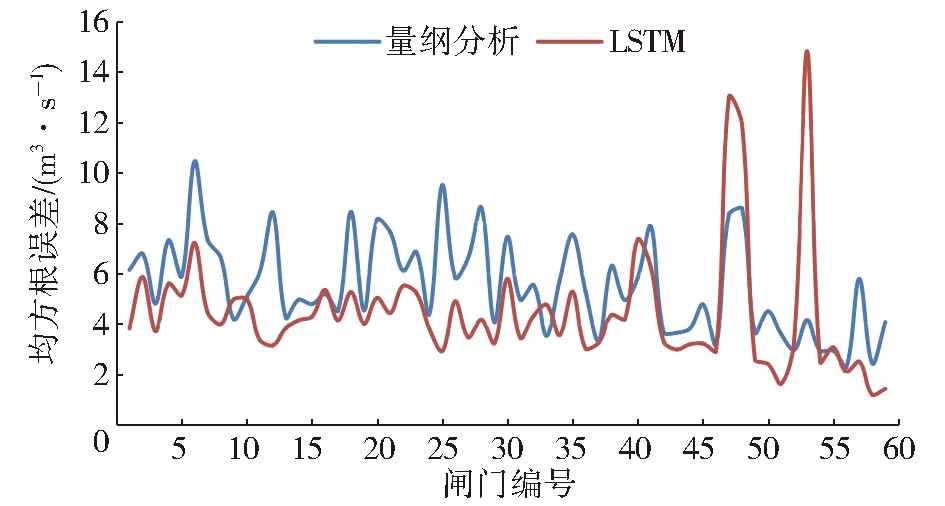
图6 流量均方根误差对比Fig.6 Comparison of root mean square errors of discharge

根据模型计算结果，采用纳什效率系数评估2种方法计算精度，其取值范围一般为0～1，值越接近1表明模型可信度越高。2种方法计算所得纳什效率系数结果见表2。

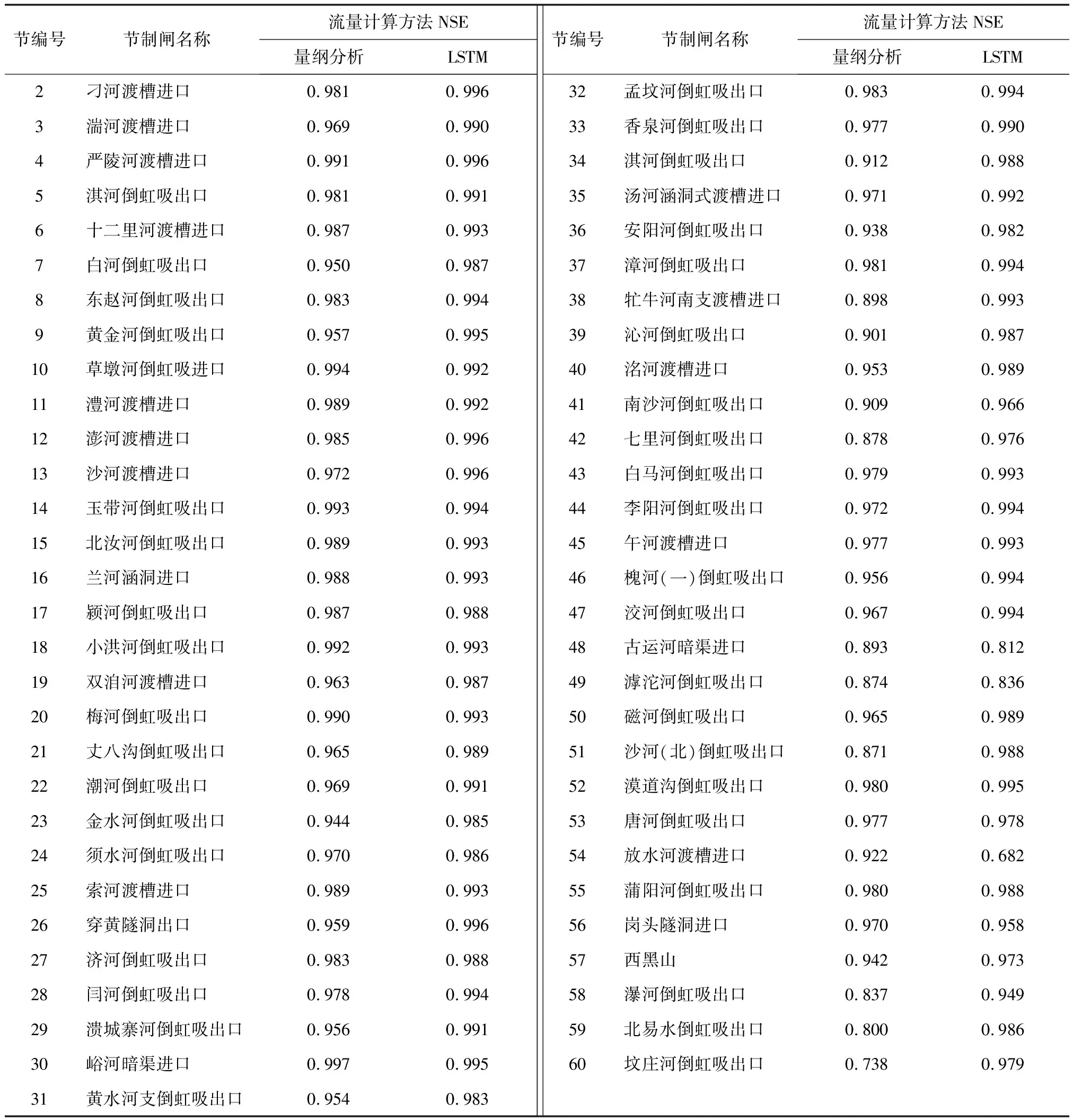
表2 2种方法纳什效率系数对比Tab.2 Comparison of the Nash efficiency coefficients (NSE) of the two methods

通过以上结果图表可以得出如下结论。

量纲分析法：对于安阳河以南的上、中游节制闸(36号节制闸以前)，闸门流量计算平均绝对误差5 m3/s左右，平均相对误差4%左右，均方根误差6 m3/s左右，纳什效率系数约0.97；对于安阳河以北的中、下游节制闸，流量平均绝对误差3 m3/s左右，平均相对误差2.8%左右，均方根误差4.8 m3/s左右，纳什效率系数约0.93。

LSTM神经网络：对于安阳河以南的上、中游节制闸，闸门流量计算平均绝对误差3 m3/s左右，平均相对误差2%左右，均方根误差4.5 m3/s左右，纳什效率系数约0.99；对于安阳河以北的中、下游节制闸，流量平均绝对误差2.7 m3/s左右，平均相对误差2.5%左右，均方根误差4.5 m3/s左右，纳什效率系数约0.96。

由此可得，对工程整体而言，LSTM方法的流量计算结果略优于量纲分析法。但从工程局部上看，安阳河以南上、中游各节制闸采用LSTM方法得到的过闸流量平均绝对误差、平均相对误差以及均方根误差均小于量纲分析法，而安阳河以北有14座节制闸结果相反，量纲分析法计算得到的流量误差更小。

因此，综上结果表明：基于LSTM神经网络的流量计算方法对于南水北调中线工程大、中流量的计算更为适用。相反，量纲分析法则表现为中线工程中、下游的流量误差偏小于上游，因此表明量纲分析法更适用于工程中、小流量的计算，同时也印证了闸门过流系数率定时中、小流量确定系数更高的结果。