基于DEM的河道断面构造改进方法及洪水演进精度评估

2022-11-15张文婷李祉璇张行南刘永志

南水北调与水利科技 2022年3期

张文婷，李祉璇，张行南，刘永志

(1.河海大学水文水资源学院，南京 210098；2.水文水资源与水利工程科学国家重点实验室，南京 210098；3.南京水利科学研究院水文水资源研究所，南京 210009)

洪水灾害是自然灾害之一，常导致严重的经济损失和人员伤亡[1-2]。为了减轻洪水带来的危害，需要不断加深对洪水的研究。随着计算机科学的快速发展，越来越多的水动力学数值模型用于模拟洪水过程，如MIKE 、HEC-RAS(hydrologic engineering center′s river analysis system)等[3-5]，为防洪减灾措施的科学制定提供参考和依据。

水动力学数值模型可以得到与实际洪水演进过程较为吻合的模拟结果，需要河道断面资料用于建模，但在无河道断面地区和不方便实施河道断面测量的地区其应用受到了限制[6-7]。河道断面数据缺乏问题在许多地区都存在，尽管可以在建模前补充测量，但耗时长，花费昂贵[8]。针对这一问题，一些学者[9-11]开始探索从数字高程模型(digital elevation mode，DEM)中提取河道横断面数据应用到洪水模拟中，为缺少河道横断面数据的河段洪水模拟提供方法。在模拟中，研究者[12-16]发现从DEM中提取河道断面数据存在对河道地形的描述不够准确的问题，这将会影响洪水模拟准确性，因此,一些研究者尝试通过使用河道断面数据修正的方法对DEM数据做出调整，将河道实测断面数据整合到DEM中，从而得出理想的模拟结果[17-18]。然而实际洪水模拟中许多河段的断面数据不易获得或测量成本过高，对此，一部分研究者[19]尝试概化河道断面，使概化的断面与实测断面保持一致的水位-流量关系；也有研究者探索通过结合水面以上地形数据推求水面以下的地形，例如俞茜等[20]采用三次样条插值并合成完整断面，得到的模型结果有较高可信度。但目前缺乏对于DEM提取河道断面用于水动力学建模效果的系统研究和分析。

为此，本文在缺少河道断面资料的地区以高精度DEM数据为支撑，通过构造断面的方式快速获取能够应用于水动力学数值模型的河道横断面。分别采用由DEM直接提取河道横断面(以下简称DEM断面)、实际勘测测量河道断面(以下简称实测断面)和改进的基于DEM构造的河道断面(以下简称构造断面)，进行河道水动力学数值模型建模，利用水动力学数值模型分别进行洪水模拟试验，包括在不同频率的洪水或不同模型结构(HEC-RAS 1D,HEC-RAS 1D-2D)中，分析不同河道断面生成和获取方法对模拟结果的影响，为缺少实测河道断面资料河段的洪水模拟提供参考。

1 基于DEM的河道断面提取方法和构造方法

1.1 DEM数据直接提取河道断面

使用的地形数据由美国国家高程数据集(National elevation dataset，NED)以DEM的形式提供，其生成方式为通过航空激光扫描获取激光雷达点云数据，经过数据处理得到本试验采用的3 m×3 m分辨率的DEM栅格数据，是研究区范围内可公开获取的最高分辨率数据。DEM 被用作地形数据的输入来源以创建河道横断面等，在RAS Mapper模块中将横断面数字化，以转换为 HEC-RAS 模型所需的河道几何形状，所有几何数据都使用栅格表面的高程值进行编码，作为DEM断面的地形数据导入模型计算。

1.2 改进的基于DEM数据构造断面

基于DEM的河道横断面构造方法[21]以Bhuyian提出的DEM校正方法为基础，在河道横断面较为规则的河道中通过增大DEM断面面积来增强河道的过流能力。基本原理是利用DEM断面高岸点指定的坡度确定各断面左右岸的交点(图1)，并假定其为各断面最低点的近似位置。对于单渠道河道，边坡的坡度从高岸点处的最大值逐渐减小至零。断面最低点的近似位置确定之后，各横断面由通过断面最低点的铅直线分为左半部分和右半部分，每一部分面积相当于抛物线及其对称轴围成的面积，抛物线的垂直高度为均匀流深度y。此构造方法为断面构造的Bhuyian方法，以下简称为Bhuyian法。

比对研究区实际勘测河道横断面情况，Bhuyian法构造的断面形态较为接近实测断面，但其面积存在偏小的情况，造成过流能力不足，需要在此基础上增加构造断面的过流面积，使得构造断面与实测断面的过流能力更为接近。本文提出一种改进的断面构造方法，提出横断面最低点高程修正系数k，对横断面最低点高程进行修正，断面形态仍由左半部分和右半部分的抛物线组成，最终构造横断面的方式见图1。

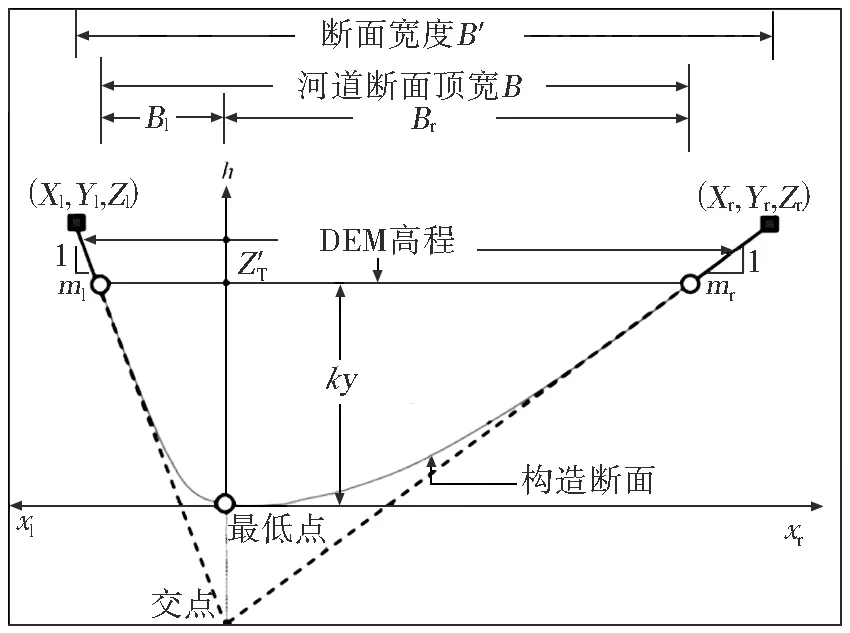
图1 横断面构造Fig.1 Schematic of section construction

构造的横截面的几何特性为

(1)

式中：B为河道断面顶宽，m；B′为断面宽度，m；y为均匀流水深，m；Zi为DEM表示的高岸坡点高程，m；Z′T为DEM最低点高程，m；k为横断面最低点高程修正系数。

断面面积为

(2)

湿周为

P=∑Pi=Pl+Pr

(3)

水力半径为

(4)

利用曼宁公式[式(5)]确定河道各断面的均匀流水深，这是一个求得参考流量的均匀流水深精确解的迭代过程[21]。

曼宁公式为

(5)

式中：Q为参考流量,m3/s；n为糙率，其取值在《水工设计规范》等设计规范的基础上结合实际河道类型及以往研究模拟中的相关取值经验[22]确定；A为断面过水面积，m2；R为水力半径，m；S为河道坡度。

河道坡度由沿着河流中心线的DEM上可用的高程确定，确定糙率时要考虑到局部特征和地形，这一过程是为了实现估计的断面最低点的纵向坡度和河道坡度值之间的最小差异。通过计算得出断面最低点的高程为(Z′T-ky)。本文所提改进的断面构造方法以Bhuyian法为基础，利用横断面最低点高程修正系数k改进构造断面的横断面面积，以下简称为改进法。

2 洪水演进模拟模型计算原理

用于河道水力计算的两个模型为HEC-RAS 1D和HEC-RAS 1D-2D，均由美国陆军工程兵团(USACE)的水文工程中心(Hydrologic Engineering Center)研发[23]。

HEC-RAS 1D中所用到的理论基础是基于Saint-Venant方程组的水流连续方程和动量方程[24]

(6)

(7)

式中：AT为过流断面面积，m2；t为过流时间，s；x为水平距离，m；Q为断面流量，m3/s；ql为单位长度的旁侧入流，m2/s；V为沿水流方向流速，m/s；g为重力加速度，m/s2；z为河道水位，m；Sf为摩阻比降，依据曼宁公式求得

(8)

式中：n为糙率；R为水力半径，m。

在一维非恒定流模拟中，HEC-RAS模型对式(6)和(7)采用四点隐式差分格式离散求解方程。

HEC-RAS 1D-2D模型由进一步扩展一维模型得到。通过建立侧向连接，将二维流动区域耦合到一维断面。

二维连续方程为

(9)

式中：H为水面高程，m；h为水深，m；u和v为分别为x和y方向平均深度上的流速，m/s；q为源项，m/s，表示外部流入(如降水)。

二维动量方程中x方向为

(10)

y方向

(11)

式中：vt为涡流黏度系数；cf为摩擦因数；f为科里奥利参数。

侧向结构上水流的流动由堰流方程或二维流动方程确定，计算侧向结构上水流流动的标准堰流方程为

dQ=C(yws-yw)3/2dx

(12)

式中：yws为水面高程；yw为侧向结构的高程；C为堰流系数。

3 实例应用

选取美国佛罗里达州迈阿密市内主河道迈阿密河作为研究案例，该河流包括一条干流和南北两条支流。

3.1 研究区概况

迈阿密河发源于佛罗里达国家公园大沼泽地，流经迈阿密的市中心，长达8.9 km，河口位置为北纬25°46′14″，西经80°11′06″，研究区面积38.8 km2。

迈阿密河流经的迈阿密市位于佛罗里达大沼泽和比斯坎湾之间，属于热带季风气候，平均最高气温一般为29～38 ℃，年降水量1 710 mm，其中大部分降水发生在6月至10月中旬。此外，该区域常受飓风影响，如2004年弗朗西斯(Frances)飓风、2017年艾尔玛(Irma)飓风。

3.2 数据

研究区域内流量和水位的观测数据来自南佛罗里达州水管理区(SFWMD)环境监测数据库，这些数据集可作为水动力学模拟的边界条件输入HEC-RAS模型。根据Anuar等[25]的研究，断面布设间距为河道水面宽度的10～20倍时对水位过程模拟结果影响较小，考虑到迈阿密河大部分河道较为平直，研究区域内自上游向下游以500 m为间距布设河道横断面，布设情况、验证站位置及边界所处位置见图2。

图2 断面布设情况、验证站位置及边界所处位置Fig.2 The distribution of cross-sections and the location of the gauging station and the boundaries

采用本文提出的改进的断面构造法和DEM数据直接提取法生成研究区河道断面。经过当地实际典型河道断面与Bhuyian法概化的横断面对比分析，发现以Bhuyian法概化的横断面其过流面积虽然有所改善，但与实测断面面积仍相差较大，通过改进法进一步扩大河道横断面面积，当最低点高程修正系数取值为1.1时，各典型断面的横断面面积相对误差均降至30%以下，缩小了约7%(表1)；若继续增大最低点高程系数的取值，部分横断面的河底高程将低于实测断面，综合考虑横断面形态特征和过流能力，将最低点高程修正系数k取值为1.1。选取位于河道上游的断面1、支流与干流交汇后的断面2、位于河道下游的断面3以及分别位于南北两条支流上的断面4和断面5，比较实测断面、Bhuyian法和改进法构造的断面，如图3所示，改进法构造的断面在表示的河道测深细节方面优于Bhuyian法构造的，更为贴近实测断面。

表1 横断面面积的相对误差Tab.1 Relative error of cross-sectional area %

图3 不同断面形式对比Fig.3 Comparison of cross-sections

3.3 水动力学模拟参数设置

运行HEC-RAS 1D模型需要河道横断面的地形资料、边界条件和糙率值。地形数据为研究区数字高程模型(DEM)，分辨率为3 m。模拟2004年飓风Frances期间(2004年9月1日00:00至2004年9月8日00:00)、2017年飓风Irma期间(2017年9月7日00:00至2017年9月14日00:00)和2014年6月17日至2014年6月24日的洪水演进过程，上边界条件为干流和两条支流的入流流量，下边界条件为各飓风期间的潮位，初始条件为上边界所在断面流量初始值，模型计算步长为20 s，模拟结果输出时间间隔为1 200 s。

在水力学模拟中，糙率是一个重要参数[26]，需要对河道和河漫滩的糙率分别赋值。根据《水工设计规范》等相关文献资料，河道糙率为0.015～0.035，河漫滩糙率为0.075～0.150，结合研究区河道受到人为干预的实际情况，糙率参数的最终取值见表2。

表2 河道横断面糙率取值Tab.2 Parameter (Manning coefficient )

HEC-RAS 1D-2D模型由HEC-RAS 1D模型耦合水流的二维流动区域得到，输入模型的数据在一维模型基础上增加了洪泛区的地形数据和糙率值，水流的二维流动区域糙率取值依据美国地质调查局(USGS)的土地利用数据(NLCD)，对不同土地利用类型分区处理。研究区内不同类型下垫面的糙率取值见表3。

表3 不同下垫面类型糙率取值Tab.3 Roughness values of different underlying surface types

本研究主要目的是研究河道横断面数据对洪水演进模拟的影响，因此,同一种水动力模型结构中的模拟设置仅有河道横断面地形数据不同，其他参数均相同。

4 结果与分析

4.1 河道水位结果和流量结果对比分析

利用HEC-RAS 1D模型和HEC-RAS 1D-2D模型对Frances飓风期间(2004年9月1日至2004年9月8日)和Irma飓风期间(2017年9月7日至2017年9月14日)的洪水过程以及2014年6月17日至2014年6月24日的低水位过程进行水动力学模拟，根据验证站处断面实测水位过程，对实测断面的HEC-RAS 1D和HEC-RAS 1D-2D模型进行模型验证。验证结果表明，HEC-RAS 1D模拟的3次水位过程均方根误差分别为0.04、0.03和0.04 m，HEC-RAS 1D-2D模拟的3次水位过程均方根误差分别为0.07、0.04和0.07 m，模拟结果的均方根误差都不超过0.1 m，模型模拟结果的偏差较小，可以在该区域进行准确的洪水模拟。将构造断面输入HEC-RAS 1D模型和HEC-RAS 1D-2D模型，其模拟水位过程见图4。

图4 验证站处采用构造断面时模拟水位与观测水位对比Fig.4 Simulated water level and observed water level with modified cross-section at the gauging station

图4显示构造断面模拟出的水位过程与实测水位过程基本吻合，计算出模拟水位过程与实测水位过程的误差(表4)，用以比较不同水动力模型结构和不同断面形态模拟洪水水位过程的差别，计算结果表明，DEM断面模拟出的水位数值和变化趋势均与观测值相差较大。在采用DEM断面的4种模拟方案中，计算水位的平均误差最高可达3.57 m，均方根误差明显高于采用构造断面的模拟方案。

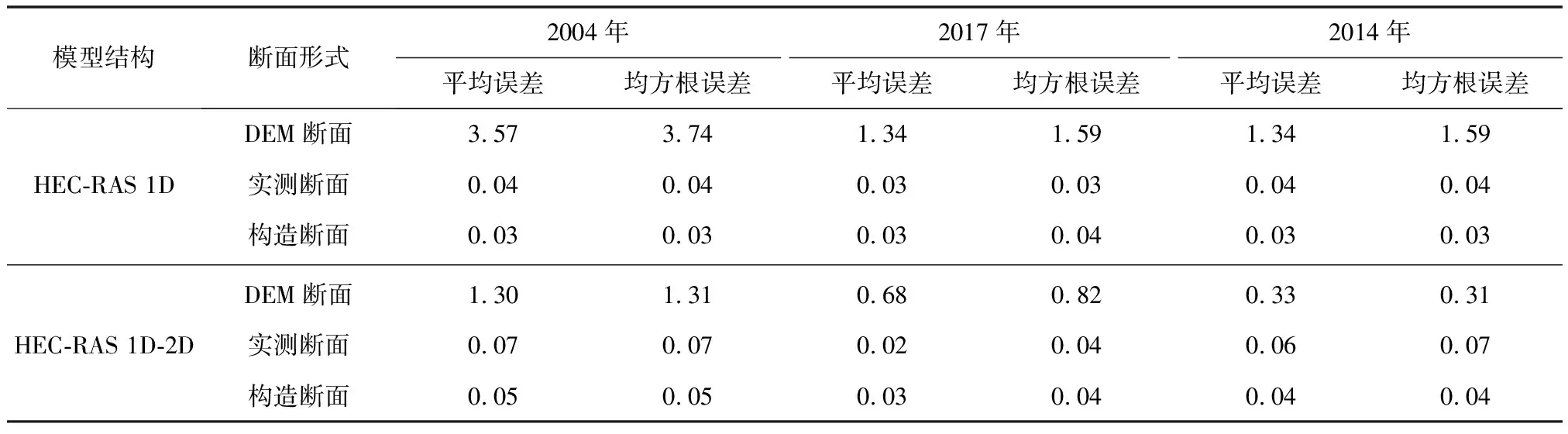
表4 模拟水位结果及分析Tab.4 Summary of simulations 单位：m

分析模拟水位误差大小与实际观测水位的关系(图5)，发现在HEC-RAS 1D模型和HEC-RAS 1D-2D模型中，实测断面和构造断面的模拟误差稳定在较低的数值，没有随水位而变化的趋势，DEM断面的模拟误差随着水位的升高呈现不断减小的趋势，当验证站处水位达到1.61 m时，DEM断面的计算误差已经小于0.1 m，而在低水位条件下，DEM断面的模型计算结果与观测值相差较大。

图5 水位模拟误差与实测水位关系Fig.5 Relationship between simulation error and measured water elevation

研究区内的验证站为水位站，缺少实测流量资料验证构造断面的准确性，但采用实测断面的HEC-RAS 1D模型经过验证可以模拟该研究区的洪水过程，故而将构造断面产生的流量过程与实测断面产生的流量过程进行比较，见图6。图6显示，在不同的水位条件下，HEC-RAS 1D模型中构造断面产生的流量过程与实测断面产生的流量过程平均误差为0.05 m3/s，HEC-RAS 1D-2D模型中两者分别产生的流量过程变化趋势及峰现时间比较接近，洪峰流量平均相对误差约为10%。考虑到偏大的模拟洪峰流量在实际应用中更为安全，偏差在可接受范围。

图6 验证站处采用构造断面与实测断面时模拟流量对比Fig.6 Comparison of simulated flow between the modified cross-sections and measured cross-sections at the gauging station

4.2 淹没范围对比

洪水的最大淹没面积由HEC-RAS 1D-2D模型中的RAS Mapper模块计算得到，图7为HEC-RAS 1D-2D 模型模拟的2017年Irma洪水过程中相应的淹没面积，在3种断面形式中，由构造断面和实测断面对应的HEC-RAS 1D-2D 模型模拟出的淹没面积和变化趋势在第72 h前比较接近，几乎同时出现最大淹没范围，两者的淹没面积仅在退水过程中略有差异，相差最大的时刻出现在第96 h，淹没面积相差约20%；DEM断面由于缺少足够的过水面积，且洪水期间上边界的来水流量较大，致使河道中的水不断地漫溢，洪泛区内洪水淹没面积呈扩大趋势，洪水的最大淹没范围产生于模拟计算结束的时刻。

分别使用实测断面、构造断面和DEM断面构建的HEC-RAS 1D-2D模型计算出洪水淹没范围，图8为这3种断面数据模拟计算的最大淹没面积对比。使用基于DEM断面的模型计算出的最大淹没范围较基于实测断面的模型产生的最大淹没范围偏大，与基于DEM断面的模型相比，使用基于构造断面的模型计算出的最大淹没范围与使用基于实测断面的模型结果十分接近。

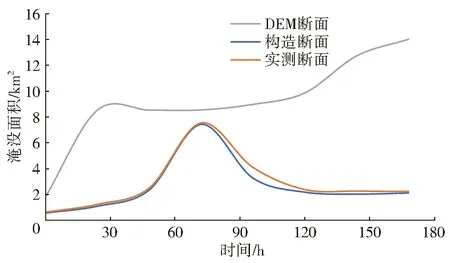
图7 不同断面形态下的洪水淹没面积对比Fig.7 Comparison of flooded areas of different cross-sections

图8 最大淹没面积对比Fig.8 Comparison of maximum submerged area

图9显示了HEC-RAS 1D-2D 模拟的Irma洪水过程中实测断面和构造断面在不同淹没深度时对应的淹没面积对比，在不同的时刻，构造断面模拟的不同淹没深度对应的面积总体与实测断面的模拟一致，约90%淹没范围水深小于1 m。

图9 实测断面和构造断面在不同淹没深度时对应的淹没面积Fig.9 Area of the measured cross-sections and modified cross-sections at different submerged depths

在HEC-RAS 1D-2D模型的4个洪泛区总计4 729个二维流动网格中选取6个淹没典型点，将构造断面与实测断面的模拟的结果进行比较。比较对象是Irma飓风期间6个典型点的淹没过程，包括洪水到达时间、淹没水深和洪水历时，结果见图10。

图10 实测断面和构造断面的淹没典型点水深Fig.10 Water depth of submerged typical points in measured cross-sections and modified cross-sections

图10显示，在二维洪泛区中构造断面产生的淹没过程和实测断面接近，HEC-RAS 1D-2D采用构造断面时能够较好地反映最大淹没水深，具有与采用实测断面时几乎相同的洪水到达时间，虽然构造断面模拟的退水过程略快于实测断面，但是在大多数淹没典型点退水时长相差不超过4 h。总的来说，通过典型点的淹没过程比较，在洪水到达时间、淹没水深和洪水历时方面构造断面能够达到与实测断面接近的模拟效果，表明采用构造断面能够在该区域进行准确的洪水模拟。