ES-MDA算法融合ERT数据联合反演地下水污染源与含水层参数

周念清，张瑞城，江思珉，夏学敏

(1.同济大学土木工程学院，上海 200092；2.上海理工大学环境与建筑学院，上海 200093)

地下水资源由于具有分布广泛、水质良好、不易受污染等特点，在人类日常生活和工农业生产中被广泛利用。然而，随着城市化进程的加快和现代工业的迅速发展，越来越多的污染物因泄漏或排放不当而进入地下水体中，导致地下水污染问题日趋严重。为了有效地治理和修复地下水污染，首先需要对污染源信息(包括污染源强度和位置等)进行准确识别。传统的地下水监测采样方法由于成本较高且获取的观测数据较少，往往难以直接获取污染源信息以及场地的水文地质参数[1-2]。现阶段的研究多通过构建地下水数值模拟模型并用求解逆问题的方式对污染源进行参数反演[3-4]。

参数反演法是通过分析多源观测信息，并与已知的参照值进行比较，不断迭代更新模型参数，使正演模型输出的观测值与参照值不断趋近，从而得到未知模型参数的近似估计，将其应用于地下水污染溯源问题中，可实现对未知污染源参数的模拟预测[5]。近年来，贝叶斯推断已被广泛地应用于地下水参数反演问题之中[6-8]。其中，基于马尔科夫链蒙特卡罗(Markov chain Monte Carlo，MCMC)方法和基于集合的数据同化方法(ensemble-based data assimilation)是贝叶斯推断的两种常见应用[9-11]。MCMC方法通过构造合适的马尔科夫链进行抽样并使用蒙特卡洛方法进行积分计算，最终收敛到平稳分布的参数后验分布，但使用MCMC方法通常需要大量调用系统模型才能达到收敛，并且模型的调用次数将随着参数维度的增加而大幅增加，给计算带来沉重的负担[12]。基于集合的数据同化算法在求解参数反演问题时，需要调用系统模型的次数相对较少，因而比MCMC算法的计算效率更高，其中集合卡尔曼滤波[13](ensemble Kalman filter，EnKF)和集合平滑器[14](ensemble smoother，ES)是其典型代表，二者的区别在于EnKF需要同时更新输入参数和状态变量，而ES仅进行参数更新，因此可以有效避免EnKF中参数和状态的不一致问题[15]。为了提高ES方法的计算效率和对高维问题的适用性，Emerick等[16]提出了一种多重数据同化集合平滑器(ensemble smoother with multiple data assimilation,ES-MDA)，利用添加扰动后的观测误差协方差矩阵对观测值进行多次数据同化，提高了算法在求解高维参数反演问题时的性能。

在利用数值模型对地下水污染物迁移转化过程进行模拟预测的过程中，模型参数的准确性是影响预测精度的关键。然而，由于模型参数存在空间变异性特点，对于非均质性很大的污染场地，难以利用稀疏的观测数据来准确反演估计污染场地的模型参数[17]。为了解决传统的勘测方法成本较高且获取的观测数据较为稀疏的问题，近年来有学者[18-19]将地球物理方法(如高密度电阻率法、地质雷达法等)引入到污染场地调查中，能够以较低的成本获取大量的连续观测数据，有效提高了参数反演方法在应对高维参数空间时的适用性。

本文提出一种基于ES-MDA算法求解地下水污染溯源问题的数据同化方法，并融合由高密度电阻率(electrical resistivity tomography,ERT)法采集的ERT观测数据进行参数反演，然后将该反演结果与传统的以浓度和水头为观测值方法而非采用地球物理方法得到的结果进行比较，验证该方法在求解高维参数反演问题时的有效性。

1 研究方法

1.1 地下水污染迁移模型

利用MODFLOW程序[20]与MT3DMS程序[21]构建地下水污染迁移的数值模拟模型，其中，MODFLOW程序可以求解饱和多孔介质中的地下水流问题，用基本微分方程表示为

(1)

式中：Kx、Ky、Kz分别为渗透系数在X、Y、Z方向上的分量，m/d；H为水头，m；W为单位时间从单位体积含水层中流入或流出的水量，d-1；Ss为贮水率，m-1；t为时间，d。

在查明了地下水流动信息的基础上，再结合MT3DMS程序，对地下水污染物的溶质运移过程进行模拟，其基本控制方程为

(2)

式中：C为质量浓度，mg/L；t为时间，d；Dij为水动力弥散系数，m2/d；vi为含水介质中的实际水流速度，m/d；qs为单位体积含水层的源汇项流量，d-1；Cs为源汇项中溶质质量浓度，mg/L；∑Rn为化学反应项总和，mg/(L·d)。

1.2 多重数据同化集合平滑器(ES-MDA)

ES-MDA算法是地下水污染溯源问题中一种常用的数据同化方法，其基本原理与ES算法类似，区别在于ES-MDA算法在运算过程中利用观测误差的协方差矩阵对观测值进行多次数据同化，实现了对参数样本的迭代更新，以更好地应对高维参数空间反演问题[22-23]。ES-MDA算法的基本步骤如下：

第一步确定数据同化的迭代次数(Na)和每次迭代对应的膨胀系数ai(其中，i=1,2,…，Na)。

第二步从模型参数的先验分布中选取Ne个样本，组成初始样本集合，M1=[m1,1,m2,1,…，mNe,1]。

第三步从i=1开始执行多次迭代计算，在第i次迭代中，对样本集合Mi=[m1，i,m2,i,…,mNe,i]中的每一个样本运行正演模型以获取该样本对应的预测值dj,i，正演模型的表达式如下：

dj,i=f(mj,i),j=1,2,…，Ne

(3)

第四步根据公式(4)对样本集合进行更新：

mj，i+1=mj，i+CMD(CDD+aiCD)-1(dobsj-dj,i),

j=1,2,…,Ne

(4)

式中：CMD为模型参数mi与预测值di之间的协方差矩阵;CDD为预测值的自协方差矩阵;CD为观测误差的协方差矩阵;dobsj为根据aiCD添加扰动后的观测值。

第五步重复执行第3步和第4步直到完成第Na次迭代，得到最终的参数样本集合MNa=[m1,Na,m2,Na,…,mNe,Na]，并从中获得对参数后验的反演估计。

1.3 耦合地下水-地球物理模型的数据同化方法

根据岩石地球物理关系构建联结地球物理信息与水文地质信息的数值模型，利用Archie公式[24]描述地层电阻率、溶液电阻率与含水饱和度之间关系，其公式基本形式如下：

(5)

式中：σt为地层总电阻率，Ω·m；σw为溶液电阻率，Ω·m；φ为有效孔隙度；Sw为含水饱和度；m为黏结指数；n为饱和度指数。

溶液电阻率与温度和溶液质量浓度等因素有关，Sen[17]综合考虑了这2种因素对溶液电阻率的影响，提出了如下模型公式：

(6)

式中：C为溶液的质量浓度，mg/L；T为溶液温度，文中假定恒为25 ℃。将式(5)与式(6)联合，便可构建地层电阻率与溶液质量浓度的数值关系。

高密度电阻率法(ERT法)作为一种常用的地球物理方法，可以通过供电电极(A、B)向地下空间输入稳定的电流I，然后根据测量电极(M、N)处的电位值V得到视电阻率的观测数据ρa，再据此推算出电阻率的空间分布。利用开源的Pygimli程序[25]构建地球物理模型并求解ERT正演问题。ERT法的正演模型可表示为

(7)

式中：ρ为地层电阻率的空间分布，Ω·m；V为电位值，V；I为电流值，A；δ(r)为狄拉克δ函数。

以上述方法为基础，提出基于ES-MDA算法融合地球物理数据的数据同化方法，通过耦合地下水-地球物理模型，将质量浓度数据转换为ERT观测值，然后利用ES-MDA算法融合ERT观测数据对未知污染源参数进行反演估计。该方法的流程图见图1。

图1 基于ES-MDA算法的数据同化方法流程Fig.1 The flowchart of the data assimilation method based on ES-MDA algorithm

2 数值算例

图2 污染场地示意图Fig.2 The sketch map of contaminated site

如图2所示，污染场地存在2个点源污染，污染物成分相同，根据场地调查情况确定位置为S1和S2，假定在模拟时间内其质量浓度保持不变，点源S1处的污染物质量浓度为60 mg/L，点源S2处的污染物质量浓度为30 mg/L。场地内共布设8个水文监测点(W1至W8)，用于测量质量浓度与水头数据，并在模拟期t为40、60、80、100、120、140、160 d时进行数据采集，共获得8个固定水头数据与56个质量浓度数据。同时，在地表布设1条水平测线(51个电极，间距2 m)与3条垂直方向的测线(位于x=24、48，72 m处)，每条测线包含20个间距为1 m的电极，共布设111个电极，并采用dipole-dipole的方式在相同的时间点测量电位数据(共有7次电流注入，电流为1 A)，共获得763个ERT观测数据。考虑到观测误差对参数反演结果的影响，设置质量浓度与水头观测值相对误差为2%，ERT观测值相对误差为5%。

针对不同类型的观测数据，设计了3组算例来对比其参数反演效果。3组算例均采用ES-MDA算法作为数据同化方法：算例1使用质量浓度与水头数据作为观测数据；算例2仅使用ERT数据作为观测数据；算例3使用质量浓度、水头和ERT数据作为观测数据。3组算例观测数据的采集时间相同，具体设置见表1。

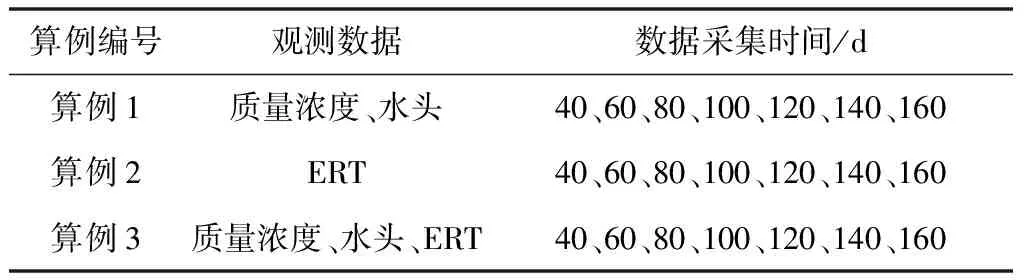
表1 算例设置Tab.1 The setting of case studies

考虑到含水层的空间各向异性，在对渗透系数场进行参数反演时计算代价往往较高。本算例中的渗透系数场根据模型的网格剖分维度为1 000维，属于维度较高的反演问题，如果直接进行求解效率会很低。因此，采用Karhunen-Loeve展开[6](KL展开)的方法对渗透系数场进行降维。

(8)

式中：ζi为独立标准高斯分布的随机数；λi和si(x,y)为特征值和特征向量；NKL为KL展开保留的项数，本算例中取NKL=60，可以保留对数渗透系数场95%以上的变异性。

利用ES-MDA算法进行参数反演的估计精度可以使用均方根误差(ERMS)来量化，该值反映了模型参数的估计值与真实值之间的差距，ERMS的值越小(趋近于0)，参数反演的精度越高。ERMS的计算公式为

(9)

3 结果与讨论

在3组算例中，潜在污染点源S1和S2的质量浓度在模拟期内保持不变，共有2个未知质量浓度参数需要识别。渗透系数场采用KL展开的方式对其降维，其中KL展开项数NKL=60，因此对高维参数场(1 000维)的识别降维成对60个高斯分布的KL展开项的反演。由此得出，对于3组算例，总共需要进行数据同化的未知模型参数数量均为62个。根据以往设计数值算例的经验，将ES-MDA算法的基础参数设置为：样本集合数Ne=1 000;迭代次数Na=7;膨胀系数ai=14、12、10、8、6、4、2(其中，i=1,2,…,Na)。

3.1 污染源源强的反演识别

图3(a)至3(c)分别为3组算例对污染源源强的反演结果。图3(a)是将质量浓度与水头数据作为观测值得到的源强反演结果，经过ES-MDA算法7次迭代后，污染源S1处的源强已基本收敛，污染源S2处的源强与真值仍有较大偏差，其主要原因是观测井数量有限，导致采集到的观测数据较少。图3(b)是将ERT数据作为观测值得到的源强反演结果，S1与S2处的源强参数均已基本收敛，且与算例1相比，反演结果更加趋近于真值，说明利用地球物理方法获取的大量ERT观测数据能有效改善传统观测方法获取数据稀疏的不足。图3(c)是将质量浓度与水头数据和ERT数据结合，共同作为观测值得到的源强反演结果，经过7次迭代后S1与S2处的源强参数明显收敛，且其与真值的拟合程度均优于算例1和算例2。

由此可得，融合ERT数据的ES-MDA算法可以更加精确地反演污染源源强，并且在此基础上添加质量浓度与水头观测数据，将使反演结果得到进一步优化，说明观测信息的数量会直接影响参数反演的效果。利用地球物理方法获取的ERT数据虽然测量精度不如质量浓度与水头数据，但可以便捷地获取大量观测信息，本案例中采集到的ERT观测数据量(763个)远多于算例1中采集到的质量浓度与水头数据量(64个)。并且，在对污染源源强的反演识别上，通过融合多源观测数据能够有效提升参数反演的精度。然后，通过量化的方式进一步比较使用不同类型的观测数据反演污染源源强的效果，将3组算例污染源源强反演结果的ERMS值列于表2中。由表2可知，3组算例是针对任一个污染源的ERMS值均呈现逐渐缩小的趋势，证明了融合多源观测数据的算例3对污染源强度的反演精度要优于算例1和算例2。

图3 污染源源强的反演结果Fig.3 The inversion results of contaminant source strength

表2 污染源参数反演结果的均方根误差Tab.2 Root-mean-square error of Case 1,Case 2 and Case 3

3.2 渗透系数场的反演识别

图4、图5和图6分别为3组算例对渗透系数场的反演结果。作为参照场的lnK真实分布如图4(a)、图5(a)和图6(a)；在反演开始阶段生成的初始随机场如图4(b)、图5(b)和图6(b)，为了对比3组算例的反演效果，采用相同的初始随机场。对渗透系数场进行参数反演得到的后验均值场如图4(c)、图5(c)和图6(c)；反映集合离散程度的方差场如图4(d)、图5(d)和图6(d)。

图4 算例1渗透系数场的反演结果Fig.4 The inversion results of hydraulic conductivity in Case 1

如图4所示，在使用质量浓度与水头数据作为观测值的算例1中，其后验均值场基本反映出lnK场的高、低值分布情况，但是对lnK场主体形态的描述还不够精细，其反演结果与参照场仍存在不小的差距。在使用ERT数据作为观测值的算例2(图5)中，其后验均值场不仅能反映出lnK场的高、低值分布区域，还能较好地刻画渗透系数场的主体形态，因此，算例2与参照场的拟合程度要优于算例1，但是在对渗透系数场分布细节的刻画上仍然不够精细。由图5(d)可以得出算例2的估计方差已趋近于0，说明继续进行迭代反演对结果的提升空间有限。在算例3中，结合ERT数据和质量浓度与水头数据作为观测值，得出的结果见图6。从图6可以明显地看出后验均值场在主体形态与细节上均较为精细地刻画出了lnK场的空间分布情况，其与参照场的拟合程度要明显优于算例1和算例2。

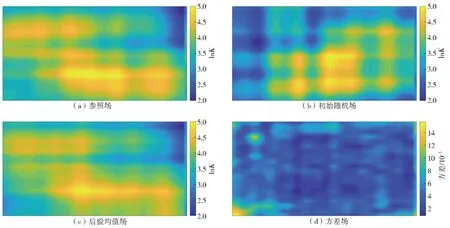
图5 算例2渗透系数场的反演结果Fig.5 The inversion results of hydraulic conductivity in Case 2

通过上述对比分析，在对高维渗透系数场反演识别上，融合ERT数据的ES-MDA算法可以得到更加精确的结果，并且在此基础上融合质量浓度与水头数据作为观测值，可以有效地提升渗透系数场的反演精度，说明利用多源观测数据在求解参数反演问题上具有明显的优势。

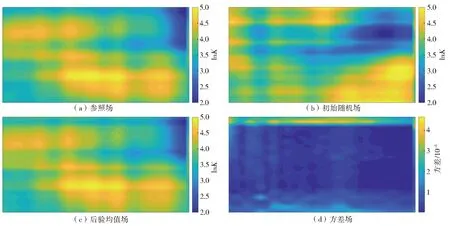
图6 算例3渗透系数场的反演结果Fig.6 The inversion results of hydraulic conductivity in Case 3

4 结论与展望

提出了基于ES-MDA算法融合ERT数据的地下水参数反演方法，并通过数值算例研究，得出以下结论：

利用ES-MDA算法融合质量浓度与水头数据或融合ERT数据，均可以实现对污染源强度和渗透系数场的联合反演，并且随着迭代次数的增加，反演结果将在一定程度上更加趋近于真实值，证明了该数据同化算法在求解地下水参数反演问题上的有效性。

通过3组数值算例来比较融合不同类型观测数据的ES-MDA算法的参数反演效果。算例1至算例3在反演污染源源强时，对任一污染源的ERMS值逐渐递减，说明反演精度从优到劣依次为算例3、算例2、算例1。算例1至算例3在反演渗透系数场时融合了多源观测数据(质量浓度、水头与ERT数据)的算例3对于lnK场主体形态和局部细节的表征要明显优于算例1和算例2；算例2对lnK场主体形态的表征优于算例1，但对lnK场细节的刻画程度与算例3仍存在差距：证明了融合多源观测数据的ES-MDA算法在求解参数反演问题上的优越性，能够有效提升参数反演的精度。

算例2中的反演结果要明显地优于算例1，其主要原因是算例2中的ERT观测数据的数量远多于算例1中的质量浓度与水头数据，即使精度略低也能够为参数反演提供更多的信息。高密度电阻率法能够快速而便捷地获取大量具有空间连续性的ERT观测数据，而传统观测方法只能在有限的观测井处获取少量不连续的观测数据。因此，在实际场地调查中ERT方法将更具优势。后续研究考虑将数据同化方法与其他地球物理方法相结合，探索更为精确高效的算法。

ES-MDA算法仅适用于对符合高斯分布的模型参数的反演求解，而对于非均质性更强、参数维度更高的非高斯场景，可以考虑结合机器学习、深度学习和多点地质统计方法，进一步探求算法的适用性和改进策略。