基于黏菌算法优化VMD-CNN-GRU模型的年径流预测
2022-11-15徐冬梅夏王萍王文川
徐冬梅,夏王萍,王文川
(华北水利水电大学水资源学院,郑州 450046)
中长期水文预报是水资源规划管理、防汛抗旱、水库优化调度的重要环节,其研究一直受到众多水文学者的广泛关注[1]。随着科学技术的不断发展,许多现代人工智能技术方法被应用于水文预报,例如BP(back propagation)神经网络[2-3]、径向基神经网络[4-5]、Elman神经网络[6-7]、支持向量机[8-9]、自适应模糊推理系统[10-11]、长短时记忆神经网络(long short-term memory,LSTM)[12-13]等。
卷积神经网络(convolutional neural network,CNN)是一种前馈式神经网络,能够充分挖掘数据之间的相关性,已被应用于物体识别[14]、故障诊断[15]、文本分类[16]等方面。门控循环单元神经网络(gated recurrent unit,GRU)是循环神经网络(recurrent neural network,RNN)衍生体系结构中的一种典型体系结构,常用于时间序列数据预测,能够解决梯度消失的问题,已在负荷预测[17]、气象要素预测[18]、风速预测[19]等领域得到应用。在径流预测方面的研究有:郭玉学等[20]利用多种递归神经网络对海岛水库进行径流预报,通过对比研究发现具有复杂神经元结构的长短时记忆神经网络和门控循环单元神经网络预报效果更好;李文武等[21]将相空间重构与变分模态分解(variational mode decomposition,VMD)和深度门控网络耦合,该模型对白山水库入库月径流量进行预测,在测试集上拟合效果较好;包苑村等[22]提出了一种VMD-CNN-LSTM组合模型,对渭河流域的2个水文站进行月径流预测,预测精度对比其他模型更优且在预测峰值和谷值上优势更为明显。为了提高传统CNN、GRU单一模型预测精度,学者们已经提出卷积神经网络和门控循环单元神经网络的组合模型(CNN-GRU)并应用于多种领域。如:姚程文等[23]将CNN-GRU模型用于电力负荷数据预测,该模型在预测精度与预测效率方面有较好的结果;党建武等[24]将CNN-GRU模型用于股指预测,有效提高了股指预测的准确率;针对出菇房室内温湿度具有非线性等特点,赵全明等[25]利用CNN-GRU模型预测出菇房多点温湿度,相比较传统的BP神经网络等CNN-GRU模型预测精度更高。
针对多数CNN-GRU混合神经网络超参数的设置方法存在精度和效率偏低的问题,本文在引入CNN-GRU组合模型进行年径流预测工作中,采用黏菌优化算法(slime mould algorithm,SMA)来确定关键参数,提出基于SMA优化的VMD-CNN-GRU组合模型对兰西水文站年径流进行预测,并构建CEEMDAN (complete ensemble empirical mode decomposition with adaptive noise)-CNN-GRU、VMD-CNN-LSTM、VMD-GRU、VMD-LSTM、VMD-PSO (particle swarm optimization)-CNN-GRU、SMA-CNN-GRU和CNN-GRU作为对比模型,以验证本文提出模型的有效性。
1 研究方法
1.1 变分模态分解算法(VMD)
VMD是2014年提出的一种新的处理信号的算法[26],分解信号的同时还能够降低输入信号中存在的噪声,因此在处理非线性非平稳序列上具有一定的优势,相较于2011年由Torres等[27]提出的自适应噪声完整集成经验模态分解算法(CEEMDAN),VMD可以有效地分离信号。VMD是给实际输入信号寻找一组最优重构的模态集合,而每个模态都被约束在一个估计的中心频率上。当给序列确定恰当的模态分解个数后,VMD就可以将非线性的原始序列分解成若干个具有不同频率并相对平稳的子序列。详细的VMD实现步骤请参阅文献[26]。
1.2 卷积神经网络(CNN)
卷积神经网络[28]是一种独特的深度网络。输入层、全连接层和输出层的结构与其他神经网络的基本相同,独特之处在于CNN拥有池化层和卷积层的结构。池化层能够筛选过滤掉多余的信息,不仅减少全连接层中的参数个数防止过拟合问题的出现,而且缩短了训练的时间。卷积层中的卷积核(过滤器)可以实现对输入矩阵自动提取特征,并且卷积层的权值将在神经元之间共享。
1.3 门控循环单元神经网络(GRU)
门控循环单元神经网络是对长短时记忆神经网络[29]进行了改进。GRU和LSTM都是通过“门”函数来进行计算的,不同之处在于GRU比LSTM少了一个“门”简化了模型结构。GRU只有两个门,即更新门和重置门。GRU与LSTM运算效果相差不大,但由于GRU参数少故计算速度更快。GRU神经网络内部结构见图1。

图1 GRU网络基本结构Fig.1 Basic structure of GRU
GRU的前向计算公式为
更新门:zt=σ(Wz·[ht-1,xt])
(1)
重置门:rt=σ(Wr·[ht-1,xt])
(2)
(3)
(4)
yt=σ(Wo·ht)
(5)

1.4 黏菌算法(SMA)
黏菌优化算法由Li等[30]于2020年提出,根据黏菌多头绒泡菌在寻找食物过程中发生的一系列动作和身体上的变化来建立数学模型。文献[28]证明了该算法在实际问题中能够快速收敛并找到最优值。详细的数学模型如下。
阶段1:接近食物。黏菌可以通过空气中的气味来寻找食物,具体用公式表示为
(6)
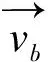
p=tanh|S(i)-DF|,i=1,2,…,n
(7)
式中:S(i)为每个黏菌的适应度;DF为迭代过程中最佳适应度。
(8)
(9)
SmellIndex=sort(S)
(10)
式中:Condition表示适应度值排在种群数前1/2的个体;r为在[0,1]上的随机数;maxt为最大迭代次数;bF(bestFitness)和wF(westFitness)为当前迭代中的最优和最差适应度值;SmellIndex为排序后的适应度值序列。
阶段2:包围食物。搜索食物时,黏菌体内会受食物浓度的影响产生一种信号。黏菌静脉接触的食物浓度越高,体内产生的波越强,细胞质流动越快,静脉变得越粗。当食物浓度较高时,该区域附近的权重较大;当食物浓度较低时,该区域的权重会降低。更新黏菌位置的计算公式为
(11)
式中:LB和UB分别为搜索范围的上下边界值;rand和r为[0,1]中的随机数。
SMA算法进行参数寻优的步骤如下。
步骤1:初始化SMA参数。设置种群规模n、最大迭代次数M、优化参数的个数及其范围,令当前的迭代次数t=1。初始化个体,随机生成n个黏菌个体的初始化位置。
步骤2:选用均方误差作为优化目标函数。将每个黏菌个体位置向量依次作为CNN-GRU模型的前提参数,根据均方误差的公式分别计算出各自对应的适应度值,然后对适应度值进行排序,选出最优和最差适应度值。

步骤4:令t=t+1。判断t是否小于最大迭代次数M,若是则重复步骤2和步骤3,反之则输出最优个体,即算法的最优解,算法结束。
1.5 组合模型构建
基于SMA优化的VMD-CNN-GRU模型的构建流程图见图2,具体的预测步骤总结如下。

图2 预测模型构建Fig.2 Prediction model construction
采用VMD方法对原始的径流序列进行分解后得到若干子序列。
建立SMA-CNN-GRU模型。设置黏菌算法中的参数,再利用黏菌算法对CNN-GRU模型的卷积层层数N、GRU层神经元个数H、训练次数E和学习率η进行参数寻优。具体步骤见1.4节。
根据建立的SMA-CNN-GRU模型对预处理后的每个分量进行拟合得到预测值。
将所有预测后的子序列进行进一步累积得到最终结果。
1.6 模型验证
采用均方根误差(ERMS)、平均绝对误差(EMA)、平均绝对百分误差(EMAP)对模型进行评价。ERMS、EMA、EMAP的计算公式为
(12)
(13)
(14)

2 实例应用
兰西站是呼兰河下游的一个水文站,断面以上集水面为27 736 km2,距河源464 km。呼兰河是松花江左岸一级支流,全长515 km,集水面积为36 631 km2。以兰西水文站1959—2014年的年径流资料为研究对象,取1959—2002年年径流数据为训练集,2003—2014年年径流数据为测试集。1959—2014年兰西水文站年径流序列见图3。

图3 兰西水文站年径流序列Fig.3 Annual runoff series of Lanxi hydrological station
2.1 VMD分解时序数据
VMD分解径流序列的关键是提前设置合适的模态个数K,不同分解个数会影响分解的结果,进而影响最终的预测结果。K值偏高可能导致模态混合或纯噪声模态,K值偏低可能导致模态的重复。通过比较各分量中心频率的方法来确定最终的模态个数K[31]。当选择不同的K值时,对兰西水文站年径流序列进行VMD分解后得到各子序列的中心频率,见表1。从表1可以看出,在K=7时,出现的中心频率3 156 Hz和3 492 Hz相差不多,说明此时可能出现模态混叠现象,所以选K=6较为合适。
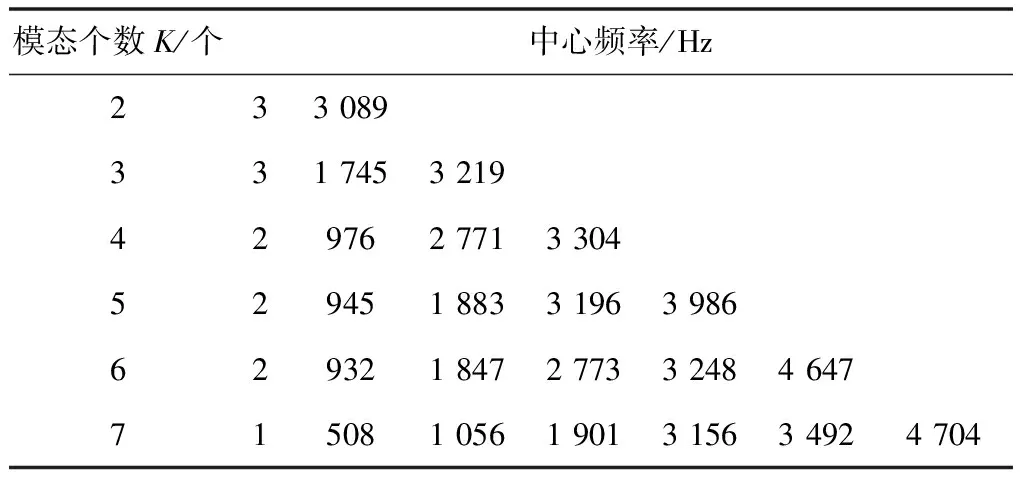
表1 不同K值对应的中心频率Tab.1 The central frequency corresponding to various K values
图4是分解后6个不同频率的子序列。对比图3原径流序列振幅变化没有明显的规律,由图4看出随着模态分量的增加,序列振幅变化呈现出周期性,序列越来越稳定,这个预处理使CNN-GRU模型可以更好地模拟数据中的特征信息并进行预测。
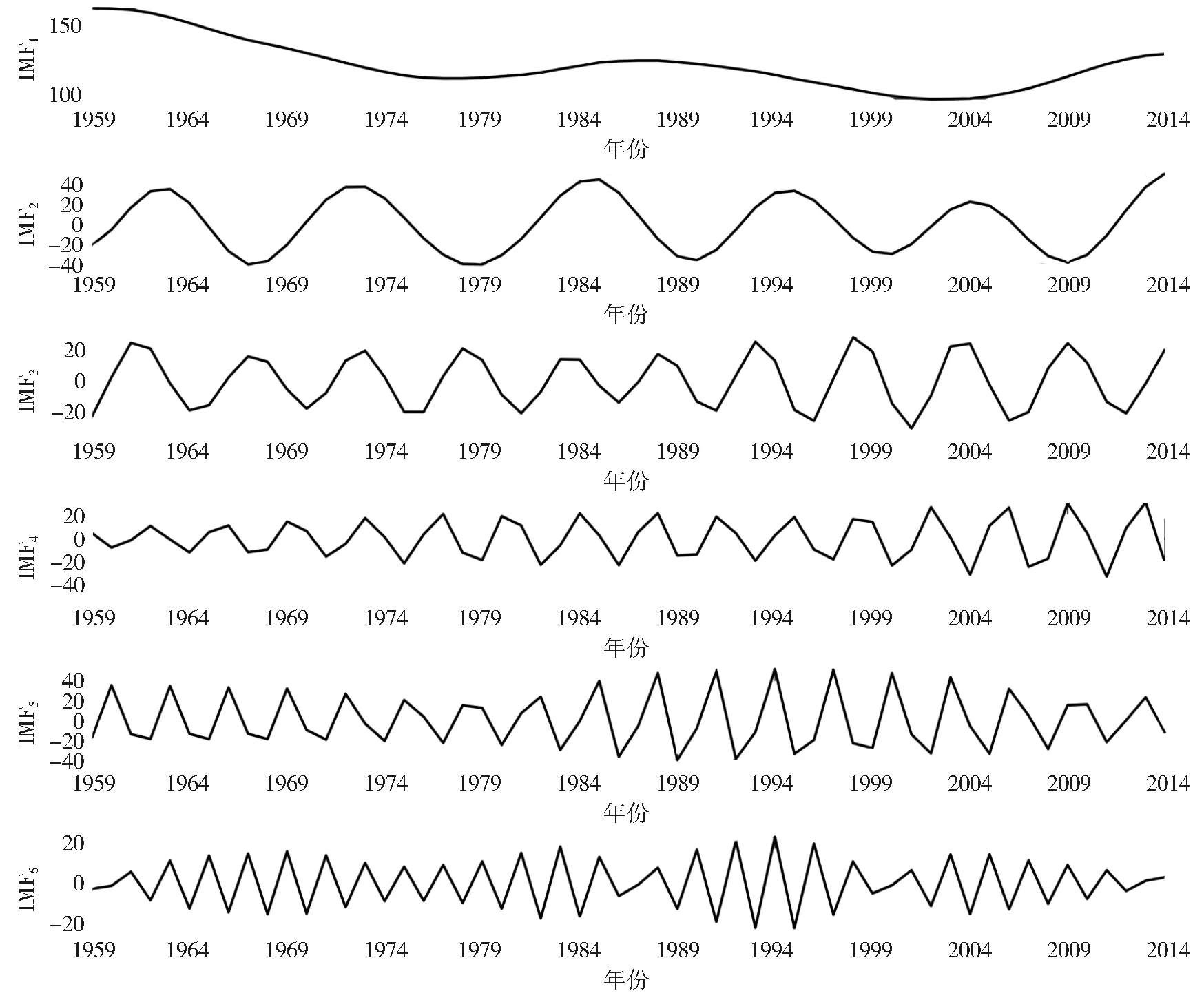
图4 兰西水文站年径流VMD分解图Fig.4 VMD decomposition diagrams of annual runoff at Lanxi hydrological station
2.2 参数设置
在CNN-GRU模型中,根据一般经验,每层卷积核的数量为上一层的两倍。根据党建武等[24]的研究,再结合本文实例得到设置不同卷积层时各层对应的卷积核个数,具体数值见表2。

表2 不同卷积层对应的卷积核个数Tab.2 Number of convolution kernels corresponding to different convolution layers
然而对于设置卷积层层数、GRU层神经元个数、训练次数、学习率的不确定性,本文提出采用黏菌优化算法来确定CNN-GRU模型卷积层层数等关键参数。设置SMA算法黏菌种群规模n=10,最大迭代次数M=20;卷积层层数N、GRU层神经元个数H、训练次数E、学习速率取值范围分别为[2,5],[100,200],[400,500],[0.005,0.010]。为了确定合适的滞时来预测当前的径流,采用自相关函数(autocorrelation function,ACF)和偏自相关函数(partial autocorrelation function,PACF)确定CNN-GRU模型的输入步长。兰西水文站年径流序列的ACF图和PACF图见图5。从图5可以看出,ACF的估计值在17时达到峰值,并且在17个滞时以后其PACF的估计值均落在95%的置信带内。因此,时间步长取17,即根据前17年的年径流来预测下一年的年径流。

图5 年径流序列ACF图和PACF图Fig.5 ACF and PACF plots of annual runoff series
由于原始序列经VMD分解后生成了6个子序列,针对不同序列该如何设置参数的问题,采用两种方案构建VMD-SMA-CNN-GRU的预测模型。方案1(VMD-SMA-CNN-GRU1)采用对不同的序列设置不同的参数,方案2(VMD-SMA-CNN-GRU2)采用对不同的序列设置统一的参数,不同方案下SMA对各子序列参数进行寻优后结果见表3。除加入优化算法的模型以外,其他6种对比模型中,卷积层层数、GRU层神经元个数、训练次数、学习率分别设置为各取值范围的中间值。因此,CNN层数为4,GRU层和LSTM层神经元个数均为150,训练次数为450,学习率为0.007 5。

表3 不同方案下SMA对各子序列参数寻优结果Tab.3 Optimization results of sub-sequence parameters by SMA under different schemes
2.3 结果分析
采用实测数据逐步分析验证。利用训练好的CNN-GRU模型先提取训练集中最后17年的数据,以预测第一个新值,接着取第二个所预测数据前面17年的实测数据来计算当前年的预测值,重复上述操作直至预测完验证期全部数据为止。选择2003—2014年的预报结果验证模型预测精度,即预测到第12年结束。
为了说明SMA优化的VMD-CNN-GRU模型的优势,使用CEEMDAN-CNN-GRU模型、VMD-CNN-LSTM模型、VMD-LSTM模型、VMD-GRU模型、VMD-PSO-CNN-GRU模型、SMA-CNN-GRU模型和CNN-GRU模型作为基准进行对比。各模型预测后评价标准计算结果和对比见表4和图6。

表4 各模型评价标准计算结果Tab.4 Calculation results of each model evaluation standard

图6 各模型预测值与原序列对比Fig.6 Comparison between the predicted values of each model and the original sequence
从图6(a)可以看出优化后的VMD-CNN-GRU模型拟合效果均很好,相比较之下VMD-PSO-CNN-GRU模型的效果略差,从局部放大图中可以明显看出1988年和2013年VMD-SMA-CNN-GRU1预测结果比其他2个模型更精确。从图6(b)可以看出:VMD-SMA-CNN-GRU2模型拟合的效果最好,尤其在预测峰值的情况下;CEEMDAN-CNN-GRU模型拟合效果最差,只有曲线的大概趋势与原序列相同而具体数值与实际值相差较大。在训练期,除CEEMDAN-CNN-GRU模型以外,其他模型均达到较好的拟合效果,但通过局部放大1994年的预测结果后可以发现各模型之间还存在一定的差异,VMD-SMA-CNN-GRU2模型预测精度更高。从验证期中可以看出,VMD-SMA-CNN-GRU2和VMD-CNN-LSTM模型拟合程度优于VMD-GRU和VMD-LSTM模型。
由表4可以得出如下结果。
经SMA优化的VMD-CNN-GRU组合模型预测精度最高。对比2种不同方案下VMD-SMA-CNN-GRU的预测结果可知各子序列设置不同参数时可以提高预测精度。VMD-SMA-CNN-GRU1与VMD-PSO-CNN-GRU模型相比,ERMS、EMA分别减少了31.18 %、26.33 %,说明粒子群优化算法[32](PSO)容易陷入局部最优无法找到最优解,而SMA算法能避免这一问题并有效的寻找优化参数。
VMD-SMA-CNN-GRU2模型与SMA-CNN-GRU模型相比,ERMS、EMA和EMAP分别减少了80.13%、 82.72%和 84.84%,可以看出分解技术和优化算法均能提高模型的预测精度,但通过比较发现分解技术的提高程度更大。
VMD-SMA-CNN-GRU2模型与CEEMDAN-CNN-GRU模型相比,ERMS、EMA和EMAP分别减少了79.81%、78.66%和80.68%;与CNN-GRU模型相比,ERMS、EMA和EMAP分别减少了85.21%、87.17%和 86.99%。VMD-SMA-CNN-GRU2模型预测精度明显高于CEEMDAN-CNN-GRU模型和CNN-GRU模型,说明了VMD分解效果优于CEEMDAN。
VMD-GRU模型和VMD-LSTM模型相比预测精度相差不大,但是VMD-GRU模型与VMD-LSTM模型训练时间分别为38.55 s和57.03 s,相比训练时间缩短了32.40%,通过对比两者模型的训练时间可以发现GRU模型效率更高。GRU比LSTM训练时间短的原因是GRU模型只有两个门,模型结构简单,构建庞大的网络时更加有效。
VMD-SMA-CNN-GRU2模型与VMD-GRU模型相比,ERMS、EMA和EMAP分别减少了29.43 %、23.20%和19.95%,与VMD-LSTM模型相比ERMS、EMA和EMAP分别减少了31.33%、26.20%和26.25%。加入CNN网络后模型预测精度明显提高,这是因为CNN模型中卷积层中的卷积核(滤波器)发挥着提取数据特征作用,通过卷积提取需要的特征然后传递给GRU层或者LSTM层。
综上所述,在验证期各种模型对兰西水文站年径流预测精度存在的差异较大一些,预测效果最好的方法依次为VMD-SMA-CNN-GRU、VMD-PSO-CNN-GRU、VMD-CNN-LSTM、VMD-GRU、VMD-LSTM、CEEMDAN-CNN-GRU、SMA-CNN-GRU、CNN-GRU。年径流序列由于受多种因素的影响极其不平稳,VMD可以自适应处理年径流序列,对序列进行重构以达到去噪的效果,CNN通过提取数据内部的特征使得GRU后续能够更加高效地进行预测,而SMA算法为CNN-GRU模型确定了恰当的参数,因此VMD-SMA-CNN-GRU模型具有良好的适应性和预测性能。
3 结 论
在VMD-CNN-GRU模型中,隐含层神经元个数、训练次数等超参数的设置影响模型拟合效果,利用SMA算法对CNN-GRU混合神经网络中超参数进行寻优改善了模型的性能,避免了人工试算效率低的情况,节约了运算时间成本同时提高了模型的预测精度。
分解技术和优化算法均能提高模型的预测精度,并且分解技术的作用影响更大。径流序列具有非线性和非平稳的特点,VMD可以将原始序列分解成较为平稳的多个子序列,增加数据的同时能够更好地进行拟合。VMD与CEEMDAN相比,在分解时VMD可以自主地设置合适的模态个数,能够有效解决模态混叠的问题,使得分解精度更高进而预测结果更准确。
VMD-CNN-GRU模型同时具有CNN网络和GRU网络的优点。CNN网络可以充分挖掘数据中的特征,GRU网络适用于时间序列预测,试验结果表明两者的结合可以有效的预测年径流,为中长期径流预报提供了一种新途径。
