基于旋转多面体锥的滚动轴承智能故障诊断

李宝庆 杨路航 杨宇 程军圣

摘要：针对多面体锥分类器形成的凸包区域分类边界数量有限且无法进行不同尺度伸缩的问题，在范数向量化的基础上增加旋转因子，提出一种旋转多面体锥分类器（Rotated and Extended Polyhedral Conic Classifier，REPCC）. REPCC增加了凸包区域的分类边界数量，并且分类边界可以在每个维度上自适应伸缩，从而可以更好地拟合正类区域，提高了分类精度.在两个不同的滚动轴承数据集上进行实验验证，实验结果表明：REPCC具有更好的分类精度、鲁棒性和泛化能力，能够准确识别滚动轴承的工作状态和故障类型，可以用于滚动轴承智能故障诊断.

关键词：多面体锥分类器；旋转因子；滚动轴承；模式识别；故障诊断

中图分类号：TH 113；TH 165+.3文献标志码：A

Rolling Bearing Intelligent Fault Diagnosis Based on Rotated and Extended Polyhedron Cone

LI Baoqing，YANG Luhang，YANG Yu，CHENG Junsheng

（College of Mechanical and Vehicle Engineering，Hunan University，Changsha 410082，China）

Abstract：In order to solve the problem that the number of classification boundaries of convex hull region formed by polyhedral cone classifier is limited and it is unable to scale in different scales，a rotated and extended polyhedral conic classifier（REPCC）is proposed by adding a rotation factor based on norm vectorization. REPCC increases the number of classification boundaries of the convex hull region，and the classification boundaries can be adaptively scaled in each dimension，which can better fit the positive region and improve the classification accuracy. Experimental verification is carried out on two different rolling bearing datasets. The results show that REPCC has better classification accuracy，robustness and generalization ability，and can accurately identify the working state and fault type of rolling bearing. REPCC can be used for intelligent fault diagnosis of rolling bearing.

Key words：polyhedral conic classifier；rotation factor；rolling bearing；pattern recognition；fault diagnosis

滚动轴承是机械设备的关键部件，长期在复杂多变载荷环境下高速運行，工作环境恶劣，极易发生故障，直接影响机械系统的总体性能[1].因此，滚动轴承故障诊断研究具有重要意义，已得到许多学者的广泛关注[2-3].

滚动轴承智能故障诊断的核心是模式识别，随着近年来人工智能技术的快速发展，滚动轴承智能故障诊断方法的研究也迅速发展[4].人工神经网络（Artificial Neural Network，ANN）、支持向量机（Support Vector Machine，SVM）等方法被广泛应用于滚动轴承故障识别，取得了良好的效果[5-6].特别是深度学习（Deep Learning，DL）可以利用深层神经网络结构直接从原始信号中提取特征，近几年已在滚动轴承智能故障诊断领域获得广泛应用[7-8].但是，这些智能诊断方法也存在一些问题，其中：神经网络和深度学习需要大量的训练样本，而工程实际故障大多为小样本[9]；SVM方法对核的选取不敏感，确定核参数和惩罚系数需要花费较多的时间，另外，由于引入核函数计算，当处理大样本或者样本数据本身维度相对较高时，会遇到核函数计算缓慢的问题.

合正类区域.本质上，REPCC等基于PCF的分类模型具有与线性SVM相似的性质和复杂性，都是基于统计学习理论的有监督机器学习方法，可以使用与SVM相关联的凸二次规划问题进行最大边距训练求解.但是，REPCC等分类模型不需要引入核函数，并能够保证较高的识别率，在参数选择上比SVM更加便捷.

当滚动轴承出现故障时，其振动信号的时频分布与正常情况不同，振动信号的时域和频域统计参数通常被用作滚动轴承故障诊断的特征[13].本文将REPCC应用于滚动轴承故障诊断，首先提取振动加速度信号的时域和频域特征作为候选故障特征；然后采用距离评估技术[14]（Distance Evaluation Technique，DET）筛选候选故障特征中的敏感特征，DET通过有效因子来评估特征在样本类别变化时的敏感程度，选择类间变化明显和类内变化小的特征，评估因子越大特征越敏感；最后将筛选后的敏感特征作为分类器的输入特征，输入到REPCC进行故障识别.

在两种不同的滚动轴承数据集上开展实验验证，分析REPCC的识别精度、鲁棒性和泛化能力.通过对比实验，与PCC和EPCC相比，REPCC具有更高的识别精度、更好的抗干扰能力、更好的泛化能力.REPCC可以有效识别滚动轴承的工作状态和故障类型，在小样本情况下具有更优越的故障识别性能.

1多面体锥分类器及其扩展型

1.1多面体锥分类器

在n维向量空间R中，PCF可以用来分割不相交的两个点集，对于测试样本x∈R，分类函数定义如下：

式（1）所示的函数是一个多面体锥，其顶点位于（a，-γ）∈R×R，PCF的每个水平截面都是凸多边形.三维向量空间下的PCF示意图如图1所示.

从图中可以看出，在平面g=0上，多面体锥的四个锥面将平面分为内部区域和外部区域，由四条线性边界包围构成，这四条边界包围的区域可以看作是一个封闭的二维凸包，此时在凸包内部区域的点映射到超平面上的值g小于0，外部区域的点映射到超平面上的值g大于0，实现线性可分.因此，当一个二分类数据集样本特征维度为2，且其正类分布较为紧凑，负类分布较为分散时，一个二维PCF就能够很好地对其实现分类拟合.当样本特征维度大于2 时，与二维类似，PCF会在特征空间形成封闭凸包，并在更高维空间形成决策项来实现分类.

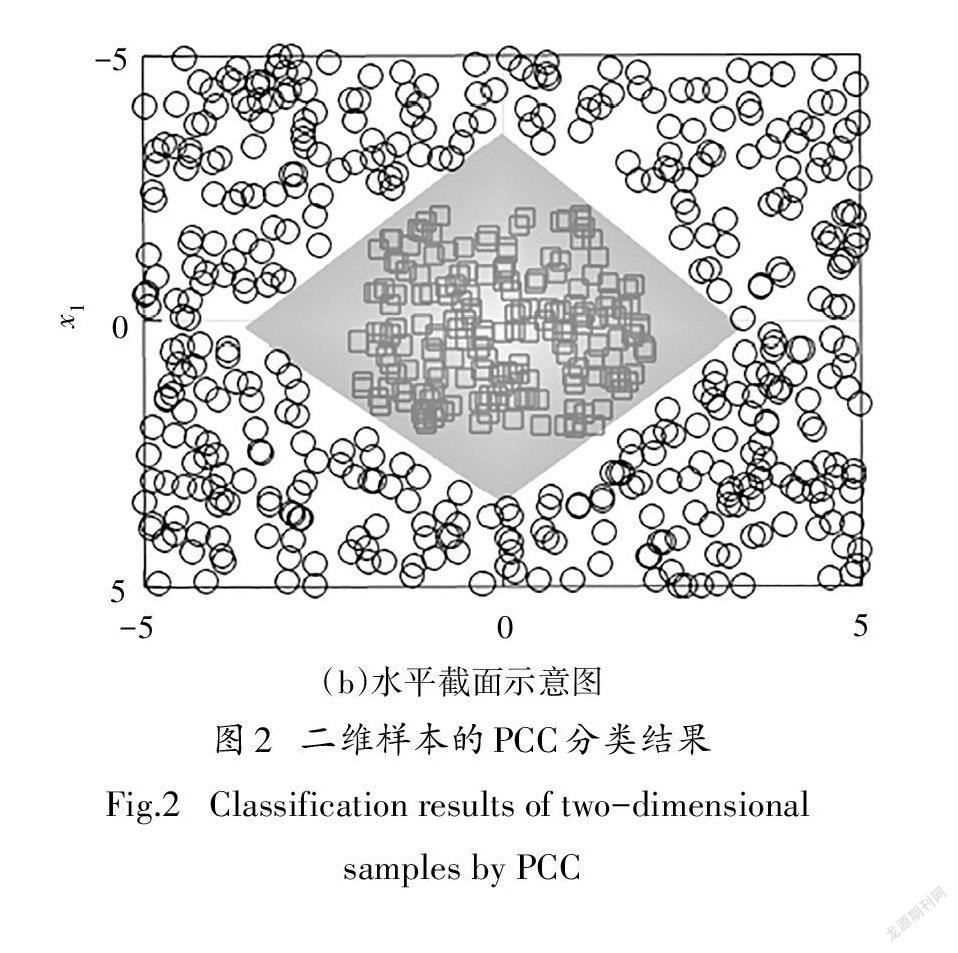
为直观表示PCC的分类特点，随机生成二维数据样本点，方框点为正类，圆圈点为负类，然后使用PCC进行优化分类，分类结果如图2所示.从图中可以看出，分类边界完全线性，实现了对随机样本点的正确分类.

1.2扩展型多面体锥分类器

EPCC中的ξ是一个属于R空间的向量，其几何意义为：分类截面所形成的凸包顶点在n个维度上的不同伸缩因子.因此，PCC中的ξ为常数，只能实现分类截面整体尺度的缩放，而EPCC的分类边界则更加灵活，可以调整凸包边界实现对正类样本的更好拟合.当ξ向量的每个值都相等时，EPCC就退化成了PCC.

对于测试样本x，g（x）<0属于正类，g（x）>0属于负类.对PCC进行最大边界训练，对于正类样本强制g（x）<-1，负类样本g（x）>+1.为了实现这种方式的训练，对样本特征向量和目标函数进行向量维度的扩展，对于PCC而言，将特征向量扩展为如下形式：

权重向量扩展为：

由于权重变化为负的，所以对于正类样本f>0，负类样本f<0.

同样地，对于EPCC而言，将特征向量扩展为如下形式：

权重向量扩展为：

2旋转多面体锥分类器

2.1旋转多面体锥函数

虽然EPCC可以使得分类决策的凸包边界能够在每个维度上实现不同权重的伸缩，改善了原始分类区域拟合正类样本的精度，但是EPCC的分类边界数量始终等于向量维度的2倍，以二维特征向量分类为例，形成的分类边界是四边形，分类边界只有4 条，有限的分类边界仍然无法保证对所有正类样本进行充分地拟合，来实现更高的分类精度.

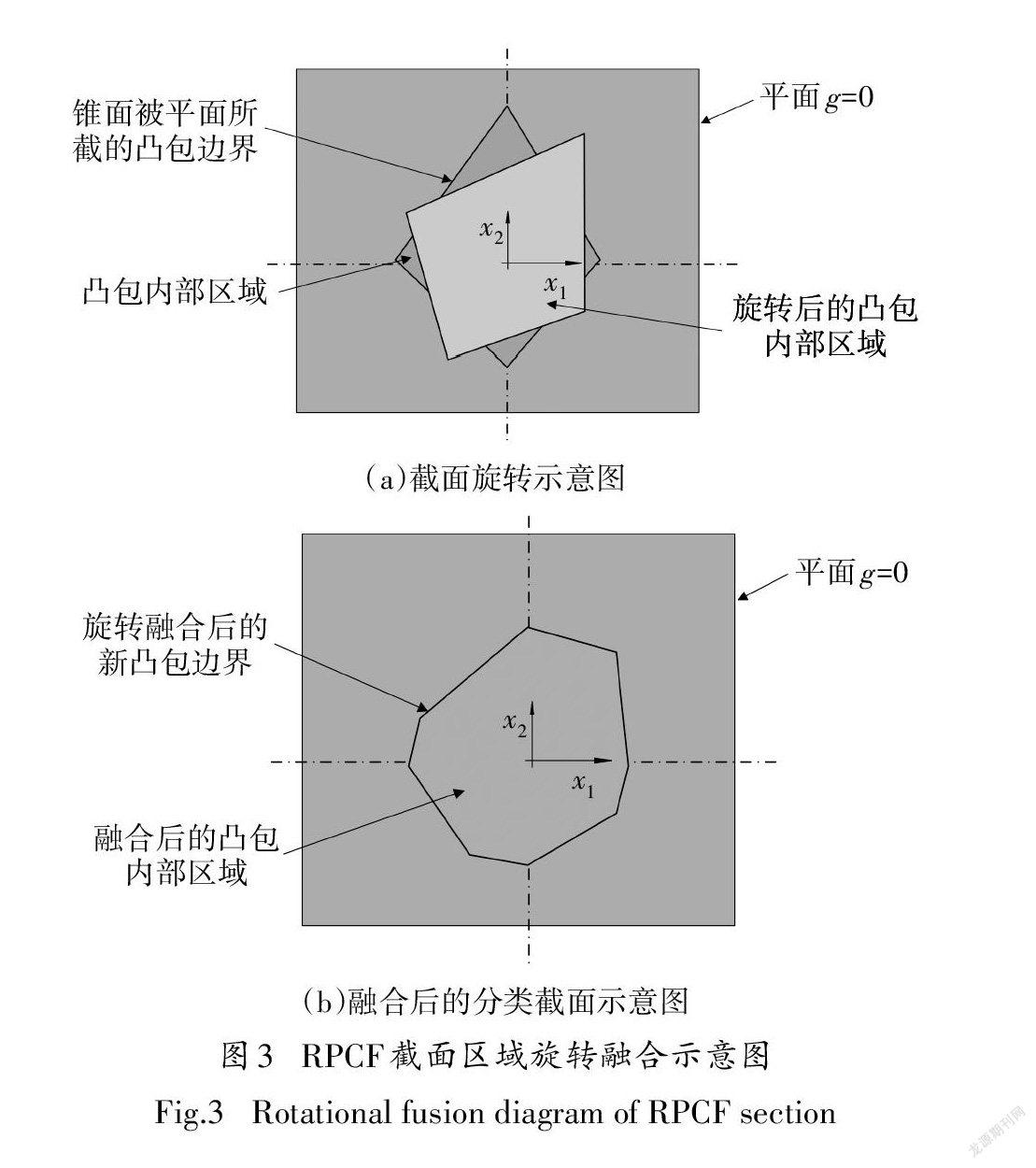
为了扩大分类截面多边形的边数，从而使得分类截面能够更好地拟合正类区域，将坐标轴进行旋转，然后融合重新绘制在原始的坐标轴中，形成新的凸包区域，得到旋转多面体锥函数（Rotated Polyhedral Conic Function，RPCF）.三维向量空间下，RPCF截面区域的旋转融合过程如图3所示.从示意图中可以看出，原始锥面形成的凸包边界只有4条，融合后的凸包边界增加到了8条，并且对于新的凸包区域，凸包上的8个顶点同时能够在四个方向维度上进行不同比例的伸缩，从而更好地拟合正类区域.

2.2旋转因子计算

基于RPCF定义REPCC，公式如式（9）所示.式中，A是维数为n的旋转变换矩陣，即旋转因子，μ是一个权重向量，ξ和μ控制四个维度方向的伸缩尺度.

在高维空间进行坐标旋转须保证旋转因子A是正交矩阵[15].在二维笛卡尔坐标系中，旋转因子A的形式如式（10）所示.坐标绕原点的旋转可以通过原始坐标向量和坐标变换矩阵相乘得到，如式（11）所示.其中，0≤θ≤π，x表示在原坐标系中x逆时针旋转θ弧度得到的新坐标.

在n维空间中，在两个特征维度的坐标系上的旋转因子A可以采用一个n维的单位方阵表示，如式（12）所示.

由于是在n维空间进行旋转，需要两两组成子坐标空间进行旋转，共有n（n-1）/2组子空间，因此需要将每个子空间的旋转矩阵进行左乘.旋转因子的计算流程如表1所示.

选择一个初始的旋转角度0，根据表1计算相对应的旋转因子A.确定旋转因子后，与PCC和EPCC的变换策略相同，REPCC将特征向量扩展为式（13）所示的形式，将权重向量扩展为式（14）所示的形式.

REPCC变换后的特征向量和权重向量的维度是原始的3倍，属于R空间.分类截面的边界数量是原始边界数量的2倍，并且继承了EPCC的优点，可以实现分类截面在2n个维度上的不同尺度伸缩，可以拟合出更为合理的正类区域，从而提高分类精度.

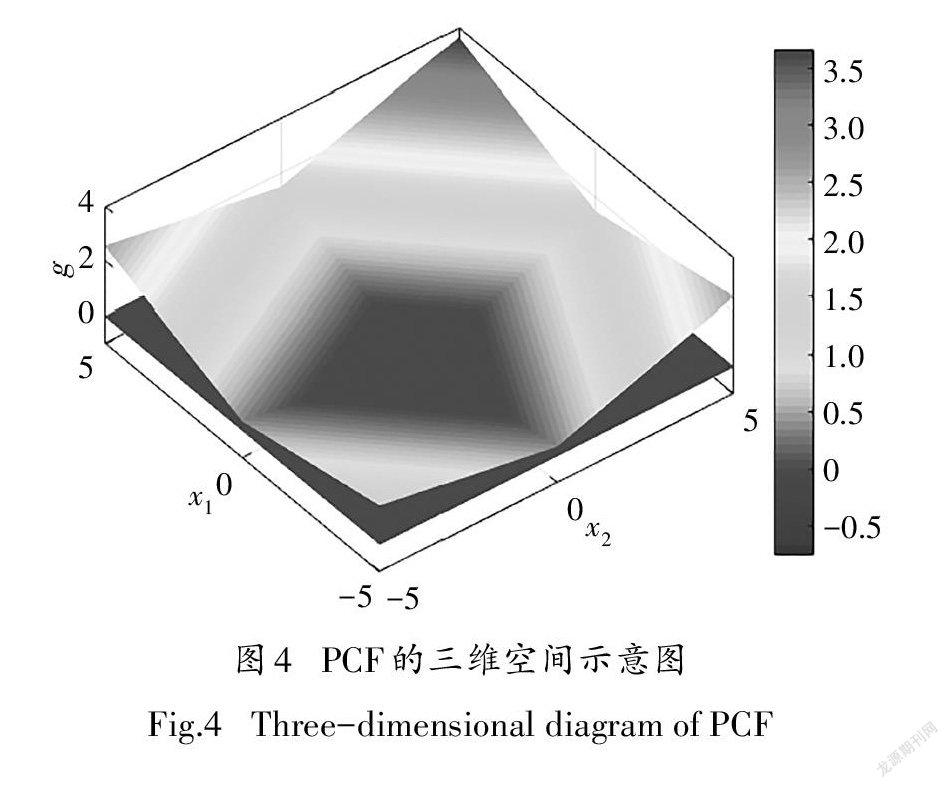
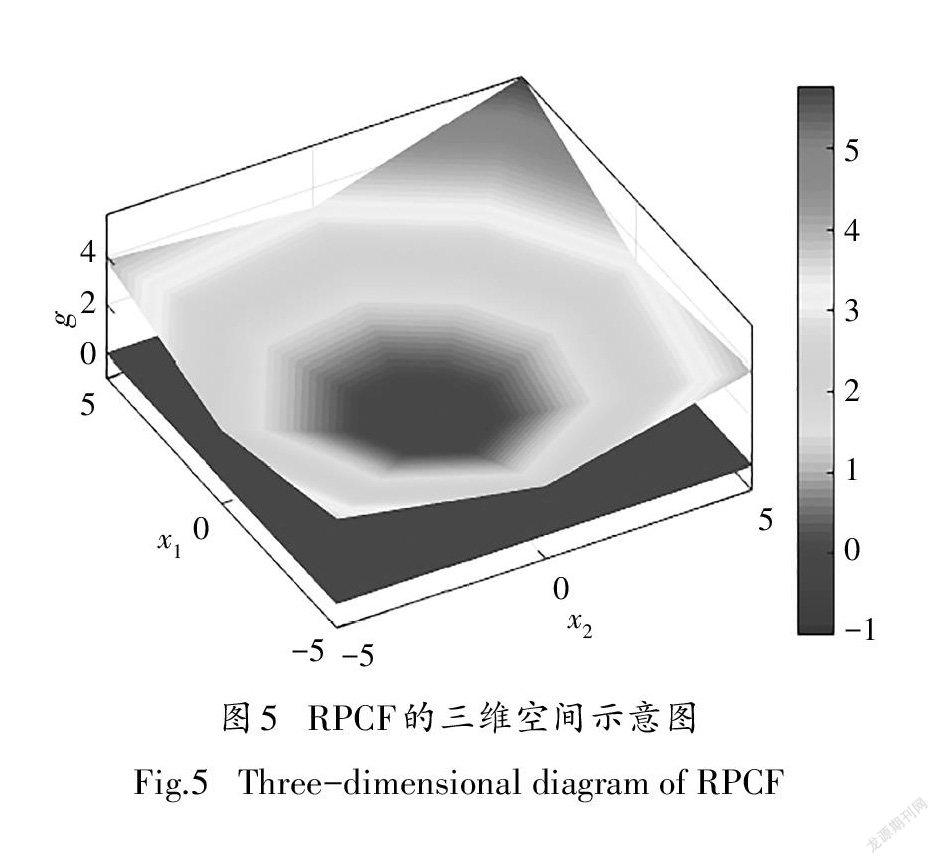
为直观表示，根据式（1）给出一个二维特征的分类函数，具体参数如式16所示，该仿真信号的三维空间示意图如图4所示.根据REPCC，给定一个初始旋转角度后计算旋转因子，其三维空间示意图如图5所示.

从图4中可以看出，PCF在平面g=0形成的二维凸包区域存在4条线性边界，分别为：0.44x+0.44x-2.76≤0，0.22x-0.22x-0.12≤0，0.44x-0.22x-1.44≤0，-0.22x+0.44x-1.44≤0.

从图5中可以看出，经过旋转融合后的多面體锥函数在平面g=0形成的凸包区域存在8条线性边界，RPCF能够以更加合理的尺度形成新的凸包边界来拟合正类样本.

2.3多分类模型

根据决策函数，PCC、EPCC和REPCC三种分类器的±1边距都转化为类似SVM方法的±1边距，采用凸二次规划算法进行最大边距训练，可以得到支持向量，然后根据决策函数逆变换获得权重向量.目标函数如式（17）所示.

式中：y为样本的类别标签，对于正类y=1，负类

采用一对多的策略将二分类问题推广到多分类模型，对于m类问题，以当前类为正类样本，其他类为负类样本，构造m个分类器进行训练[16].当进行新样本的预测时，将样本输入到每个分类器中，以输出值最大的那个分类器对应的正类类别作为新样本的最终决策.决策函数如式（19）所示.

3基于REPCC的滚动轴承故障诊断

3.1基于REPCC的故障诊断步骤

选取滚动轴承振动信号的时域和频域统计参数作为故障诊断的特征.时域统计参数选取16个，具体有：均值、方根幅值、均方根值、峰值、标准差、偏斜度、峭度、峰度指标、裕度指标、波形指标、脉冲指标、方差、最大值、最小值、峰峰值、绝对平均值.频域统计参数选取8个，具体有：频率均值、频率均方根值、频率斜度、频率峭度、频率方差、频率标准差、中心频率、重心频率.时域和频域统计参数共计24个.

不是所有的特征都对区分不同的滚动轴承故障敏感，因此在进行分类训练时，需要从候选特征中选择对故障敏感的显著特征.DET方法通过有效因子来评估特征在样本类别变化时的敏感程度，可以有效提取候选特征中的敏感特征.

基于REPCC的滚动轴承故障诊断的主要步骤如下：

1）采集滚动轴承不同故障状态的振动加速度信号，并将每种故障状态的数据分为训练样本和测试样本，训练样本和测试样本各占50%；

2）提取振动加速度信号的时域和频域统计参数，共计24个特征参数，进行归一化处理后构建候选特征集；

3）采用DET方法从候选特征集中筛选敏感特征，评估因子的阈值设置为全部特征评估因子的均值，选择大于评估因子阈值的敏感特征作为故障特征，构建新的特征集；

4）将经过DET筛选后的特征集输入REPCC中进行训练和测试，进行滚动轴承故障诊断.

3.2实验数据集

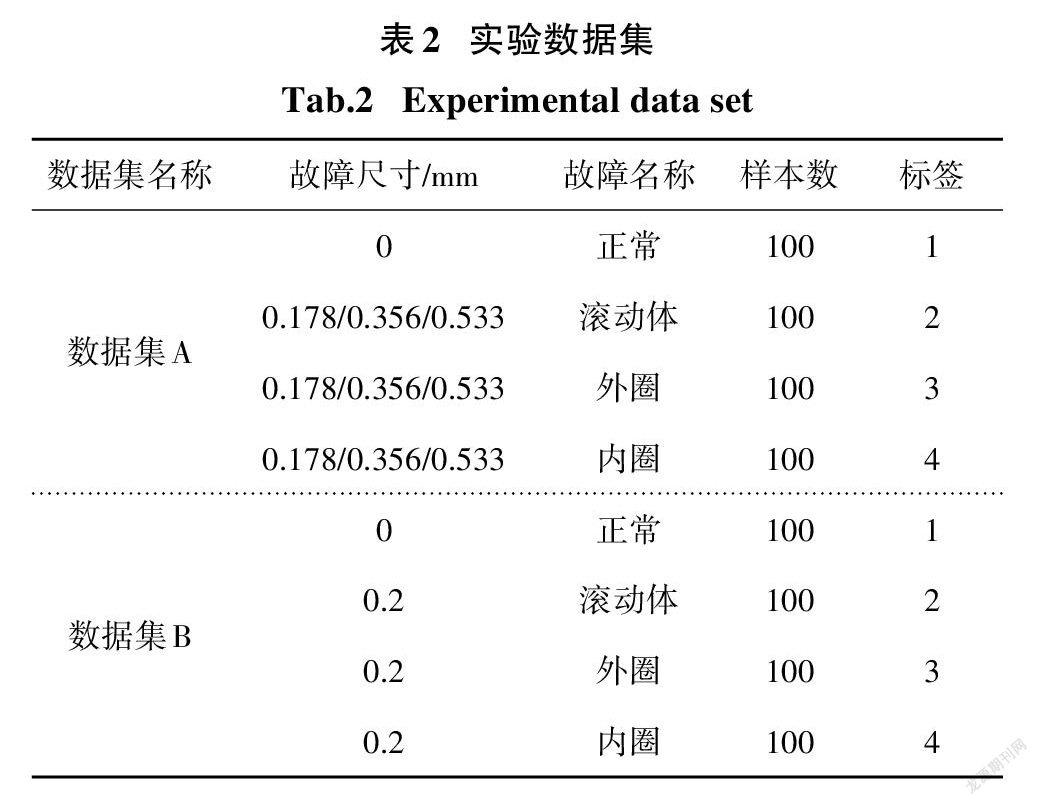
为验证基于REPCC的滚动轴承故障诊断方法的有效性和优越性，采用数据集A和B两个实验数据集进行分析验证，具体如表2所示.

数据集A的数据来源为美国凯斯西储大学轴承数据中心，实验轴承为型号6205-2RS的SKF深沟球轴承，采用电火花加工设置单点损伤，本文采用的数据是驱动端轴承的振动加速度测试数据，采样频率为48kHz，电机转速为1 797 r/min、1 772 r/min、1 750 r/min、1 730 r/min，以每12 000个数据点划分为一个样本，总共400个样本.

数据集B的数据来源于旋转机械故障实验台的实际测试数据，实验滚动轴承型号为6205-2RS- SKF，实验台如图6所示.所有的故障均采用激光切割加工，故障深度为0.2 mm，电机转速为986.1 r/min，采样频率10 kHz，以6 000个数据点作为一个样本，总共400个样本.

3.3特征集构建

为更加客观地体现REPCC的分类性能，不对采集得到的振动加速度信号进行处理，直接提取其时域和频域统计参数作为候选特征集.然后，采用DET方法从候选特征集中筛选敏感特征构建新的特征集.在进行敏感特征筛选时，选择大于评估因子阈值的敏感特征作为故障特征，评估因子的阈值设置为全部特征评估因子的均值，有效因子的计算方法参照文献[14].

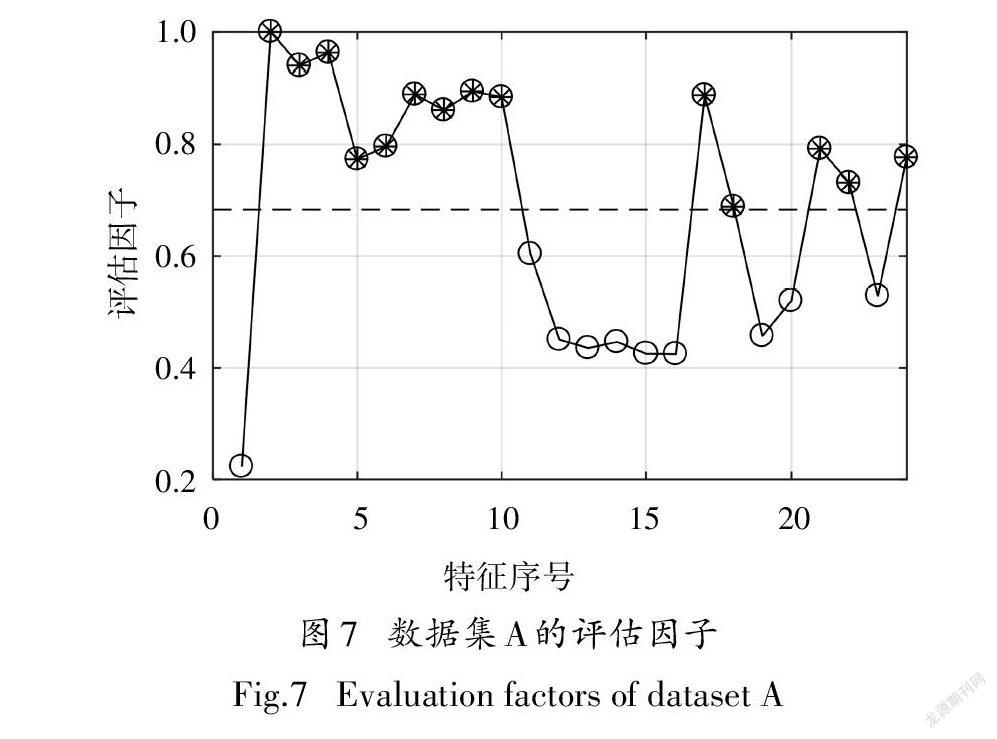
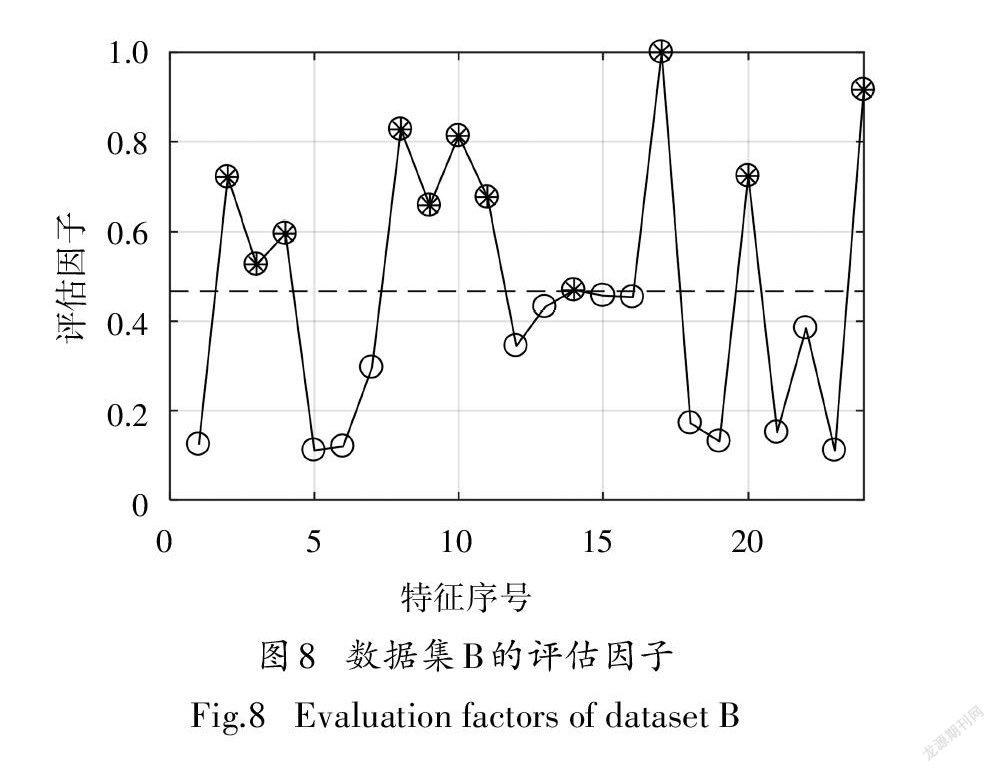
数据集A和数据集B经过时域和频域特征提取并进行归一化后，各个特征的评估因子及其均值如图7～图8所示.

在图7-8中，黑色虚线为平均值，是评估因子阈值，选择评估因子位于黑色虚线上方的特征构建新的故障特征集.从两图中可以看出，筛选后重新构建的特征集的维数下降，数据集A的特征维数从24下降为14，数据集B的特征维数从24下降为11.由于数据集A和数据集B的故障尺寸设置以及电机转速等试验工况不同，因此经DET筛选后构建的故障特征集不同.

3.4实验结果及分析

将经过DET筛选构建的新特征集输入分类器进行滚动轴承智能故障诊断.为验证REPCC的有效性和优越性，在表2所示的两个数据集上采用SVM、PCC、EPCC和REPCC进行分类识别，考察不同分类器的识别精度、鲁棒性和泛化能力.

3.4.1分类器的识别精度

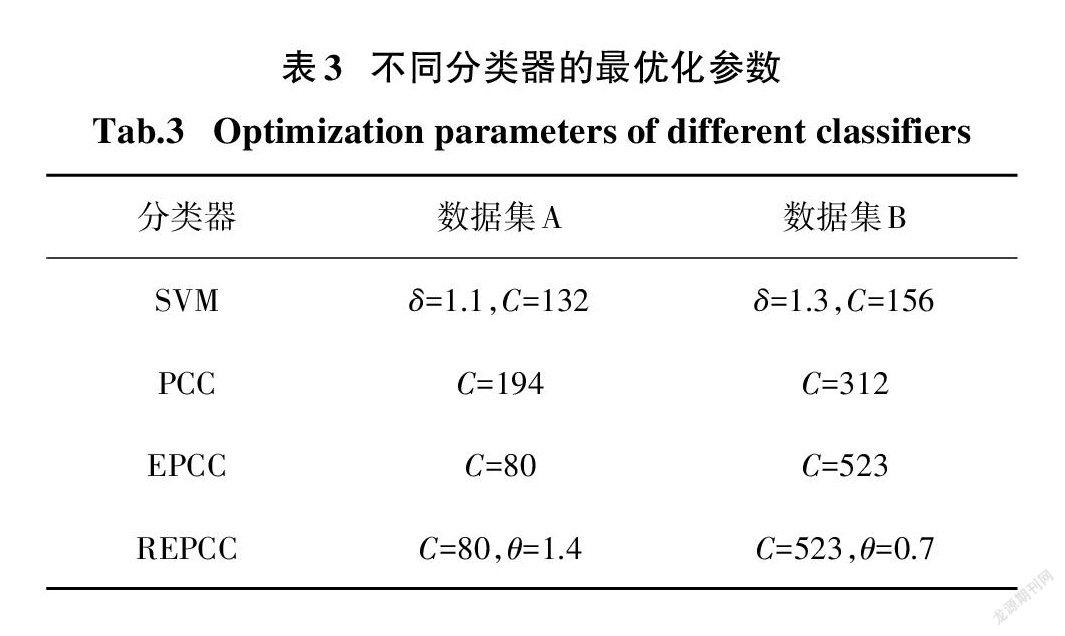
在使用不同的分类器时，需要确定分类器所需的相关参数.SVM需要确定的参数为高斯核参数δ和惩罚系数C采用网格搜索法获取最优参数.PCC和EPCC无须进行核计算，需要确定的参数为惩罚系数C.由于引入了旋转因子A，REPCC需要确定的参数为惩罚系数C和旋转弧度θ，采用控制变量法，旋转弧度0在EPCC的惩罚系数C基础上进行优化选择.

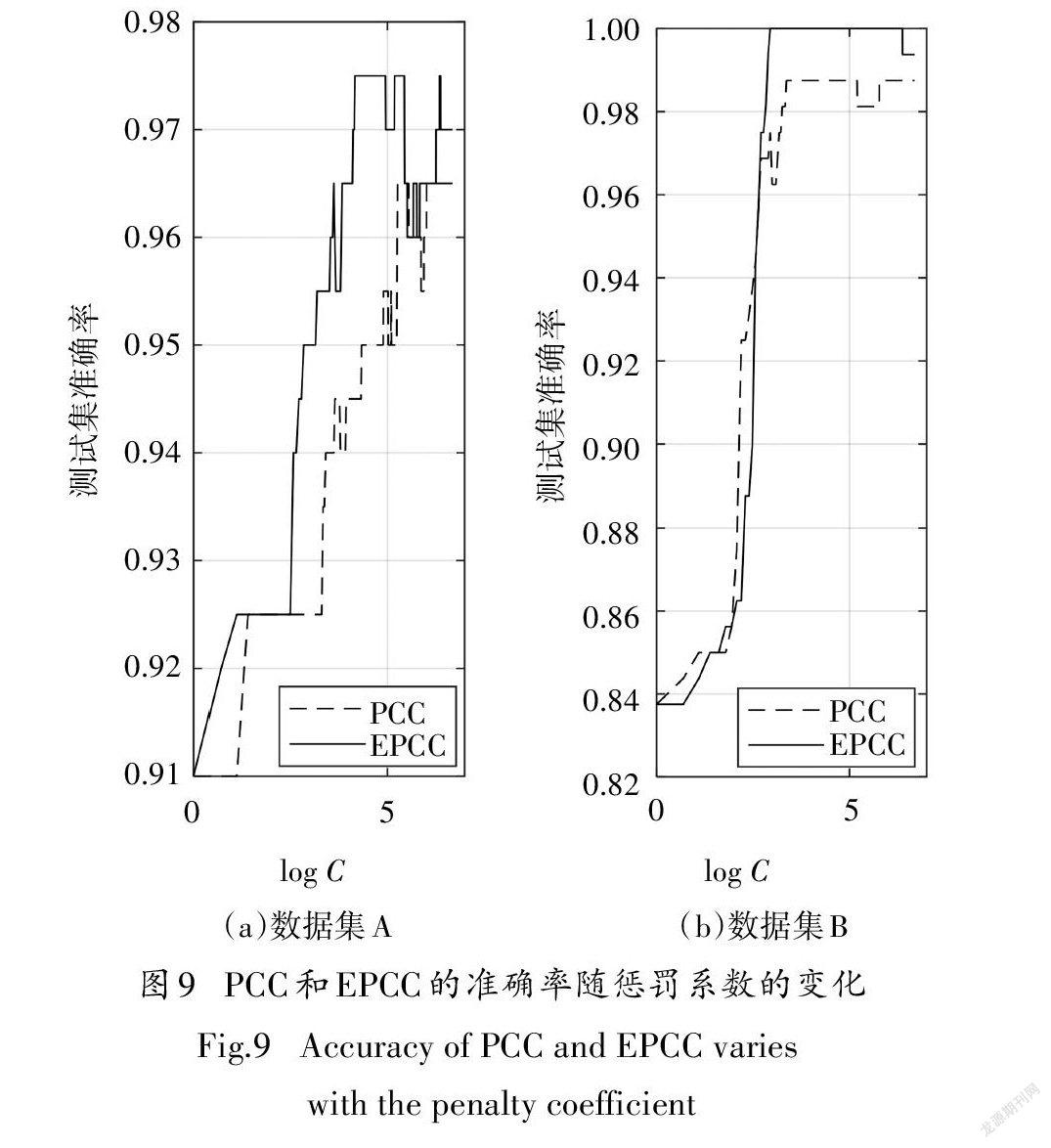
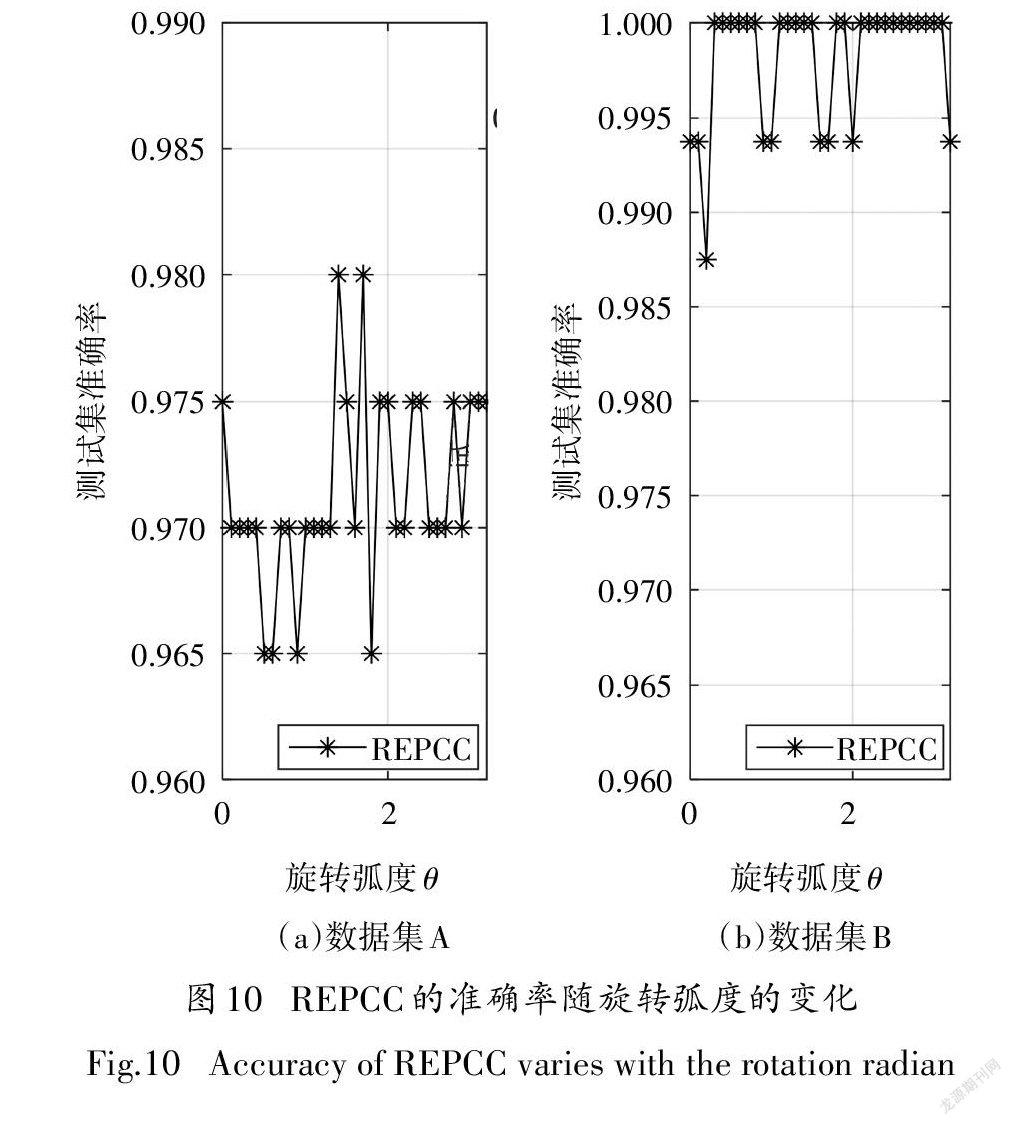
在数据集A和数据集B上，对DET筛选后的数据特征集进行五折交叉验证实验，独立重复30次，统计测试数据30次的平均准确率.PCC和EPCC的识别精度随惩罚系数C的变化如图9所示.对于REPCC，在EPCC惩罚系数C的基础上，REPCC的识别精度随旋转弧度e的变化如图10所示.利用图9 和图10选择最优化参数，各分类器确定的最优化参数如表3所示.

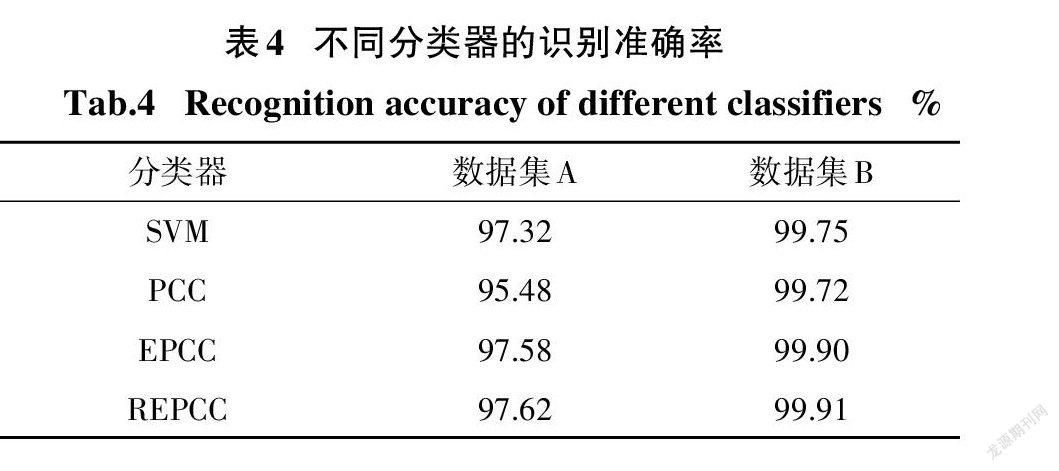
为分析REPCC的识别精度，在表3所示的最优化参数下，随机独立重复30次实验，得到平均识别准确率如表4所示.从表4中可以看出，在两个滚动轴承实验数据集上，REPCC的识别准确率最高，优于改进前的PCC和EPCC的识别准确率，也优于SVM的识别准确率.实验结果表明，REPCC具有更高的识别精度.

从表2中可以知道，与数据集A相比，数據集B的试验工况更加单一.从表4中还可以看出，各分类器在数据集B上的分类精度都高于数据集A，符合实际情况.

3.4.2分类器的鲁棒性

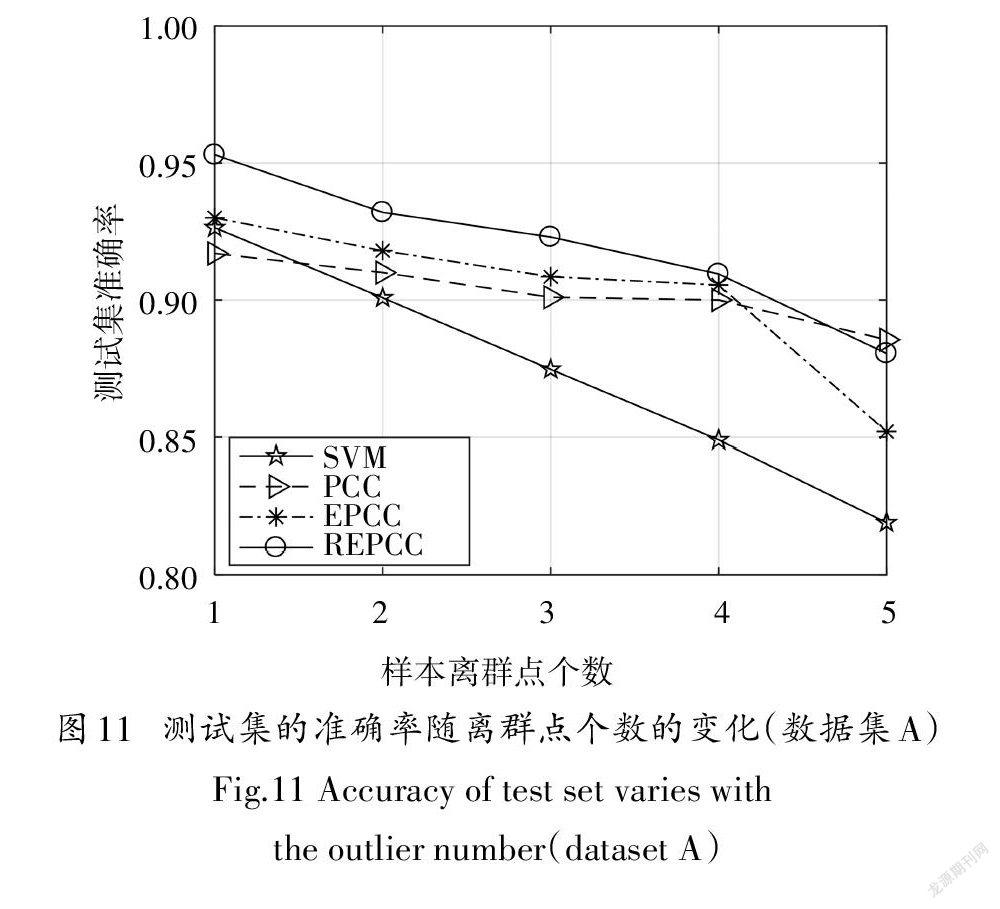
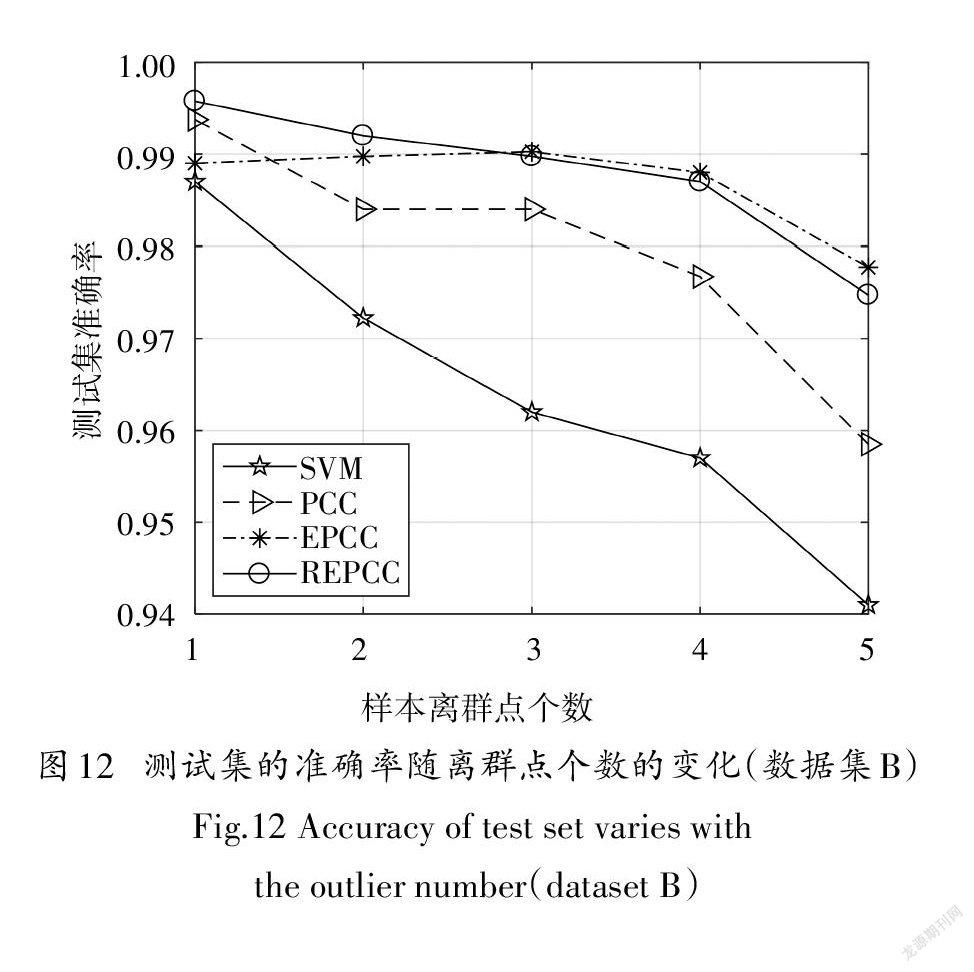
为分析REPCC的鲁棒性，在两个滚动轴承实验数据集上进行添加离群点实验，从其他类的训练样本中随机选择m个样本作为离群点，添加到当前类的训练样本集中再进行训练，然后验证测试样本的识别准确率.对于不同的m值，每次都随机独立重复30次，然后统计测试样本的平均识别精度.实验结果如图11和图12所示.

从图11和图12中可以看出，在两个滚动轴承实验数据集上，随着训练集中混杂的离群点个数增加，测试集的识别准确率都出现下降，SVM的下降程度最严重.图11和图12对比分析可以看出，对于不同的数据集，PCC和EPCC的下降趋势变化较大，REPCC的下降趋势基本一致.整体来看，REPCC的下降趋势最低，表明REPCC具有更好的鲁棒性.

3.4.3分类器的泛化能力

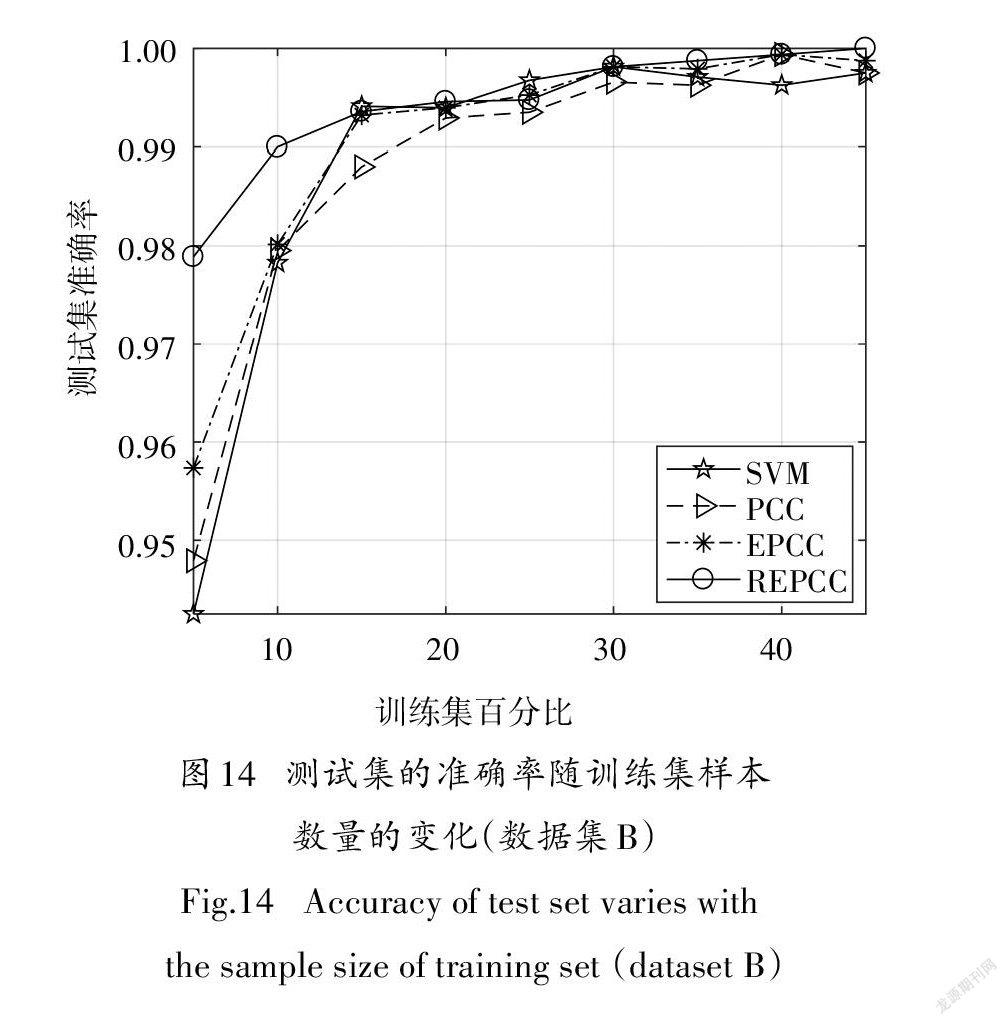
为分析REPCC的泛化能力，在两个滚动轴承实验数据集上，以不同的数量样本作为训练集，分析测试样本集的识别准确率随训练集样本数量的变化情况.对于两个实验数据集，每种故障状态的数据分为训练样本和测试样本，随机选取其中一半为训练样本，其余的为测试样本.在训练样本中根据不同比例构建不同数量样本的训练集.在最优参数下，不同样本数量的训练集每次随机独立重复30次，然后统计测试样本的平均识别精度.实验结果如图13和图14所示.

从图13-14中可以看出，两个数据集的趋势基本一致，随着训练样本数量的增加，各分类器的识别准确率也增加；REPCC的识别准确率最高，而且在训练样本较少的情况下REPCC的优势更加明显，识别准确率大于其他分类器.REPCC不仅提高了PCC和EPCC的分类精度，而且具有更好的泛化能力.

4结论

本文在EPCC的基础上引入旋转因子，提出了REPCC模式识别方法，并将其用于滚动轴承智能故障诊断.REPCC增加了分类边界数量，并且分类边界可以在每个维度上自适应伸缩，改进了分类精度，并且具有更好的抗干扰性能和泛化能力.在两个滚动轴承数据集上进行实验验证，结果表明REPCC可以准确识别滚动轴承的工作状态和故障类型，REPCC可以用于滚动轴承智能故障诊断.

REPCC是一种二分类约束算法，但是其分类模型也可以作为一种单分类模型，在后续的研究中可以寻找一种在只有单一样本分布下的模型优化求解算法，实现单分类.

参考文献

[1]王玉静，吕海岩，康守强，等.不同型号滚动轴承故障诊断方法[J].中国电机工程学报，2021，41（1）：267-276.

WANG Y J，LYU H Y，KANG S Q，et al. Fault diagnosis method for different types of rolling bearings [J]. Proceedings of the CSEE，2021，41（1）：267-276（In Chinese）

[2]程军圣，马利，潘海洋，等.基于EEMD和改进VPMCD的滚动轴承故障诊断方法[J].湖南大学学报（自然科学版），2014，41（10）：22-26.

CHENG J S，MA L，PAN H Y，et al. A fault diagnosis method for rolling bearing based on EEMD and improved VPMCD [J]. Journal of Hunan University （Natural Sciences），2014，41（10）：22-26.（In Chinese）

[3] QIAO M Y，TANG X X，LIU Y X，et al. Fault diagnosis method of rolling bearings based on VMD and MDSVM [J]. Multimedia Tools and Applications，2021，80（10）：14521-14544.

[4]ALSHORMAN O，IRFAN M，SAAD N，et al. A review of artificial intelligence methods for condition monitoring and fault diagnosis of rolling element bearings for induction motor [J]. Shock and Vibration，2020，2020：8843759.

[5] LI B，CHOW M Y，TIPSUWAN Y，et al. Neural-network-based motor rolling bearing fault diagnosis [J]. IEEE Transactions on Industrial Electronics，2000，47（5）：1060-1069.

[6]YANG Y，YU D J，CHENG J S. A fault diagnosis approach for roller bearing based on IMF envelope spectrum and SVM[J].Measurement，2007，40（9/10）：943-950.

[7]LI X，ZHANG W，DING Q. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism[J].Signal Processing，2019，161：136-154.

[8]JIA F，LEI Y G，LIN J，et al. Deep neural networks：a promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data [J]. Mechanical Systems and Signal Processing，2016，72/73：303-315.

[9]SHAO H D，JIANG H K，ZHANG X，et al. Rolling bearing fault diagnosis using an optimization deep belief network [J]. Measurement Science and Technology，2015，26（11）：115002.

[10] OZTURK G，TAHIR CIFTCI M.Clustering based polyhedralconic functions algorithm in classification[J].Journal of Industrial & Management Optimization，2015，11（3）：921-932.

[11] CEVIKALP H，YAVUZ H S.Fast and accurate face recognition with image sets[C]//2017 IEEE International Conference on Computer Vision Workshops.October 22-29，2017，Venice，Italy.IEEE，2017：1564-1572.

[12] CEVIKALP H，TRIGGS B.Polyhedral conic classifiers for visual object detection and classification [C]//2017 IEEE Conference on Computer Vision and Pattern Recognition.July 21-26，2017，Honolulu，HI，USA.IEEE，2017：4114-4122.

[13]程軍圣，郑近德，杨宇，等.基于部分集成局部特征尺度分解与拉普拉斯分值的滚动轴承故障诊断模型[J].振动工程学报，2014，27（6）：942-950.

CHENG J S，ZHENG J D，YANG Y，et al.Fault diagnosis model for rolling bearing based on partly ensemble local characteristicscale decomposition and Laplacian score[J].Journal of Vibration Engineering，2014，27（6）：942-950.（In Chinese）

[14] GEORGOULAS G，LOUTAS T，STYLIOS C D，et al.Bearing fault detection based on hybrid ensemble detector and empirical mode decomposition[J].Mechanical Systems and Signal Processing，2013，41（1/2）：510-525.

[15] REDI M H. Oceanic isopycnal mixing by coordinate rotation [J]. Journal of Physical Oceanography，1982，12（10）：1154-1158.

[16] VAPNIK V N.An overview of statistical learning theory[J].IEEE Transactions on Neural Networks，1999，10（5）：988-999.