长周期地震动作用下惯容⁃层间隔震结构地震响应分析
2022-11-14吴应雄郑祥浴翁锦华王林建江丽玲
吴应雄 郑祥浴 翁锦华 王林建 江丽玲





















摘要:已有研究表明惯容系统与基础隔震技术结合使用可以减小长周期地震动下基础隔震结构的动力响应,但惯容系统对层间隔震结构控制效果与基础隔震存在差异,需要进一步研究。提出将 SPIS⁃Ⅱ惯容系统应用于层间隔震结构,对惯容系统进行参数设计,通过数值分析研究长周期地震动下惯容⁃层间隔震结构的减震效果。结果表明:采用虚拟激励法求解结构的随机振动响应,能够快捷有效地确定惯容系统参数;惯容系统大大减少了隔震层位移,有效解决了长周期地震动下隔震层位移超限的问题,且随地震动幅值增大,位移减震率也随之提高;惯容⁃层间隔震系统在很好地控制上部结构响应的同时,进一步减小了下部子结构的地震响应。
关键词:层间隔震结构;长周期地震动;惯容系统;隔震层位移;位移减震率
中图分类号: TU352.12 文献标志码: A 文章编号:1004-4523(2022)05-1222-11
DOI:10.16385/j .cnki .issn .1004-4523.2022.05.020
引言
建筑隔震技术工程应用日趋广泛,其中新发展的层间隔震技术在解决结构竖向刚度突变等问题上具有良好的适用性[1]。对于隔震结构的设计大多基于普通地震动展开,但已有研究表明,长周期地震动低频分量占比较大,易与隔震结构产生共振效应,使隔震层水平位移超限,从而导致结构产生严重破坏[2⁃3]。针对长周期地震动作用下隔震层位移超限的问题,直接有效的措施是在隔震层中加入耗能装置。目前常用的耗能装置是黏滞阻尼器与调谐质量阻尼器,黏滞阻尼器可以有效降低隔震层的位移,但是其初始刚度较大导致上部结构的响应增大;调谐质量阻尼器本身物理质量较大且需要足够的空间安装,从而限制了其工程应用[4]。
近年来,惯容系统在工程领域的应用得到关注[5]。惯容系统是一种由惯容元件、弹簧以及阻尼元件组合而成的减震装置,其与传统耗能减震装置相比,其优势在于其质量增效及耗能增效特性。基于此,部分学者对惯容系统的减震性能及惯容⁃隔震混合控制体系展开了研究。Saitoh [6]研究了不同惯容形式对隔震层的减震效果,指出相较于串联布置,将惯容元件与阻尼元件平行布置可更有效地减小隔震层的位移。王云骞等[7]对比了旋转惯性双重调谐质量阻尼器(RIDTMD)与传统调谐质量阻尼器(TMD)的减震效果,表明相较于 TMD 与基础隔震混合控制结构,RIDTMD 和基础隔震混合控制结构的减震效率与鲁棒性均有提高。张瑞甫等[8]采用惯容系统作为层间隔震结构提高耗能效率的手段以控制地震响应,并给出了基于性能需求的参数优化设计方法,但该方法未考虑隔震支座的阻尼系数。 ZHAO 等[9]对摩擦摆调谐质量阻尼器隔震系统与摩擦摆惯容系统进行对比,表明摩擦摆惯容系统作为一种轻量化的惯容隔震系统,在不增加结构附加物理质量的同时,可以有效地降低结构的地震响应。 QIAN 等[10]讨论了不同布置形式 TID 的隔震性能,并通过 H2优化准则,以最小化上部结构层间位移作为优化目标进行 TID 参数设计,得到了 TID 参数的解析解。叶昆等[11]以一个2自由度的基础隔震结构为研究对象,以隔震层位移为约束条件,以最小化上部结构绝对加速度响应为优化目标,提出了基于性能需求的惯容⁃基础隔震结构的参数设计方法。
上述研究大多是基于惯容⁃基础隔震体系展开,当层间隔震结构的隔震层加入惯容系统后,其产生的减震效果可能不同于惯容⁃基础隔震体系,因此有必要针对惯容⁃层间隔震体系展开研究。沿着这个思路,首先采用随机振动分析与参数分析相结合的方法,确定了惯容⁃层间隔震的参数优化方法;接着通过动力时程分析,研究长周期地震动作用下惯容⁃层间隔震体系的减震性能。研究结果以期为工程应用提供理论基础。
1 惯容-层间隔震结构力学模型
1.1 力学模型
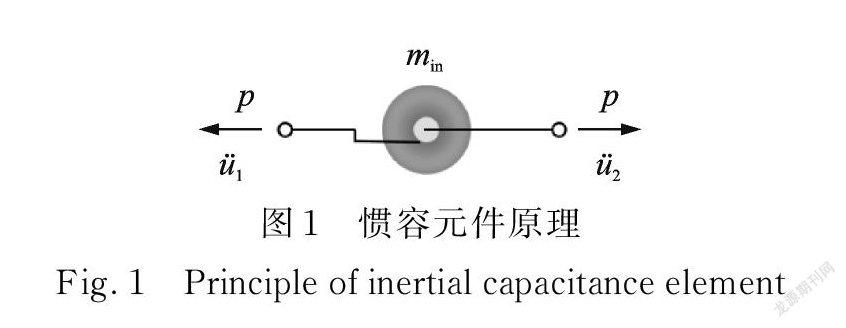
惯容系统是由弹簧元件kd、阻尼元件 cd 及惯容元件 min 根据不同连接方式组合而成的减震装置。其中惯容元件是一种两端点的质量元件,惯性力大小与两端点间的相对加速度有关,其原理如图1所示。现有研究中,最常见的惯容系统为混联Ⅱ型惯容系统(SPIS⁃Ⅱ)[12],如图2所示。为限制长周期地震动作用下隔震层的水平位移,在层间隔震结构隔震层中加入 SPIS⁃Ⅱ惯容系统,其简化力学模型如图3所示。其中,m 1,m2,k1,k2以及 c1,c2分别为下部结构及上部结构的质量、等效水平刚度和阻尼系数; mb,kb 以及cb为隔震层的质量、水平等效刚度和阻尼系数。
惯性力大小为:
SPIS ⁃Ⅱ惯容系统的出力计算如下式所示:
1.2 动力方程
由于惯容系统中惯容元件所加入的物理质量较小,其在地震作用下所产生的地震力可忽略不计[13]。根据动力平衡条件,在地震激励下惯容⁃层间隔震结构的運动控制方程如下所示:
式中 u 1,u2分别为下部结构及上部结构的位移;ub为隔震层的位移;uin为惯容两端点间的位移;ag 为地面加速度。
1.3 随机振动响应求解
为考虑地震激励的随机性,假定输入的功率谱为与实际地震动一样具有随机性的白噪声激励。惯容⁃层间隔震结构体系的均方响应可采用由惯质比μ,刚度比κ,名义阻尼比ξ等无量纲参数构成的解析表达式来表示。结构均方响应求解如下。
定义以下无量纲参数:
则安装 SPIS⁃Ⅱ惯容系统的惯容⁃层间隔震结构微分方程为:
式中fIS⁃Ⅱ=κω2(2)( ub - u1- uin)。通过拉普拉斯变换,可将微分方程转化为如下式所示的代数方程:
对线性方程组(6)进行求解,即可求出 U2,Ub,U1,Uin,其中 U2,Ub,U1,Uin,Ag 为 u2,ub,u 1,uin,ag 的拉普拉斯变换。
基于上述求解,得到主结构位移响应传递函数:
假设白噪声谱密度为 S0,根据随机振动理论,线性系统均方响应可表示为:
式中 H ( iω)为共轭复数,是结构响应的传递函数。
为简化上式积分,式(8)可转化为相应的有理函数。将结构响应传递函数表示为:
式中 s = iω;di,ei为常数。
结构的均方响应可由下式得出:
式中 an -1由下列线性方程组求解:
2 优化设计方法
2.1 性能指标
对惯容⁃层间隔震结构进行分析时,选择隔震层位移减震比γID与隔震层上部结构位移减震比γSD作为研究指标,γ ID 与γSD的表达式为:
式中σID,σSD 分别为惯容⁃层间隔震结构隔震层与上部结构在白噪声激励下的位移;σID,0,σSD,0分别为层间隔震结构隔震层与上部结构在白噪声激励下的最大位移。
2.2 参数研究
选取一个层间隔震结构作为研究对象,将该结构简化为3质点结构体系[14],简化后的层间隔震结构,其下部子结构质量为1700 t,水平等效刚度为970.24 kN/mm;隔震层质量为960 t,水平等效刚度为25.88 kN/mm;上部结构质量为2930 t,水平等效刚度为172.77 kN/mm 。通过不断改变惯质比μ、刚度比κ、名义阻尼比ξ的值,分析惯容参数对γID 与γ SD 的影响。这里固定惯质比μ为0.1,0.2和0.5,刚度比κ与名义阻尼比ξ的取值范围均为0~1。
图4为隔震层位移减震比等值线,图5为上部结构位移减震比等值线。从图中可以看出,隔震层位移减震比最优控制点位于右上角部位,即κ,ξ值的较大处,随着μ值的增大,等值线图的变化不大,而上部结构位移减震比最小值位于位于κ值较大且ξ值较小的位置。说明隔震层位移减震比与隔震层上部结构减震比这两个指标未必能同时最小化,因此在参数设计时,需要在二者之间寻找一个平衡。
2.3 参数设计策略
基于上述分析,给出了惯容系统设计策略。在该策略中,将隔震层位移减震比γID 及上部结构的位移减震比γSD 均作为设计目标。由于研究的核心目的旨在控制隔震层位移,所以将隔震层位移减震比作为约束目标,即要求隔震层的位移减震比γID 低于目标值;而将上部结构的位移减震比γSD 作为优化目标,即在隔震层位移减震比γID 满足设定目标的前提下,使上部结构的位移最小化。优化策略如下式:
在研究过程中,采用 MATLAB 数值分析软件中的内置非线性优化函数对隔震结构的隔震层位移响应进行分析,确定隔震层位移目标减震比γ ID,target。
3 算例分析
3.1 算例选取
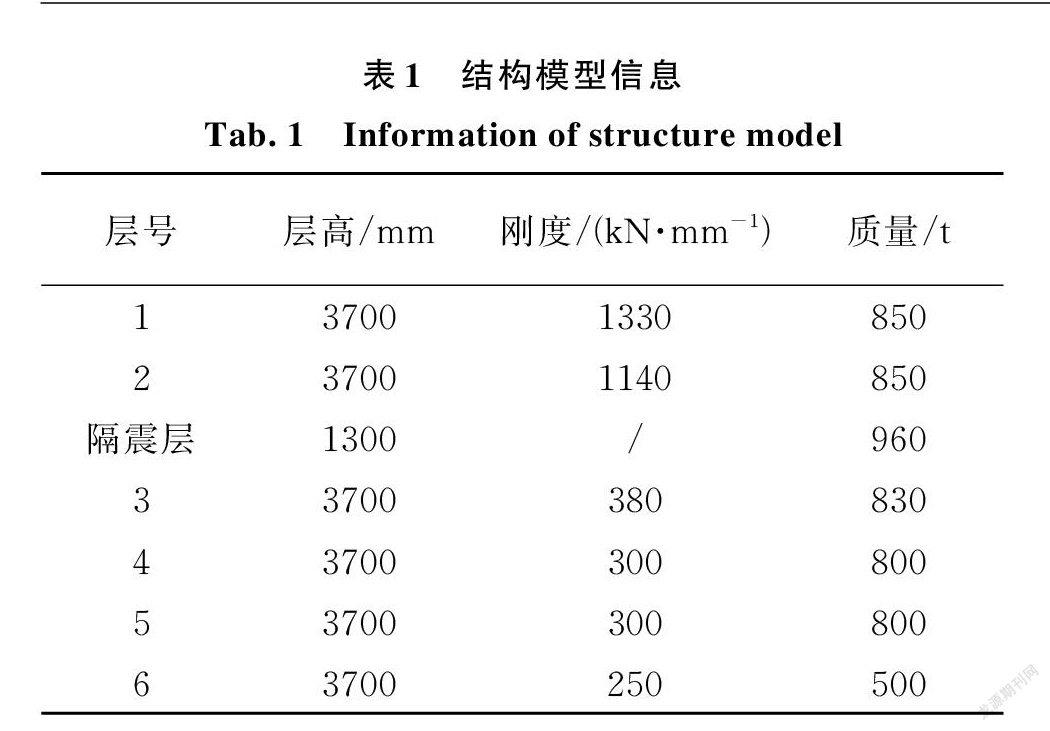
为验证惯容⁃层间隔震结构在不同地震动作用下的减震效果,选用文献[14]中的典型且具有工程应用意义的大底盘上塔楼结构进行分析,其下部底盘2层,上部塔楼4层,层高均为3700 mm ,钢筋混凝土框架结构,模型示意图如图6所示,结构基本信息如表1所示。场地类别Ⅱ类,抗震设防烈度为7度,地震峰值加速度0.15g 。非隔震模型结构自振周期为0.92 s,隔震后(中震)自振周期为2.58 s 。结构模型简化为多质点模型。为解决塔楼与大底盘处刚度突变引起的不利影响,将隔震层设置于底盘和塔楼的交接处,隔震层采用14个直径500 mm 的铅芯橡胶支座(LRB500)与6个直径600 mm 的普通橡胶支座(LNR600),隔震支座具体参数如表2所示。
隔震层在变形时通常表现为非线性,为使隔震层的恢复力特性更符合实际情况,在后续时程分析时均采用Bouc ⁃ Wen 模型来表示隔震层恢复力模型[15]。根据文献[14,16],模型结构隔震层的Bouc ⁃ Wen 模型参数如表3所示。
根据上述惯容系统参数设计方法与层间隔震结构模型信息,对惯容⁃层间隔震结构的地震响应进行初始分析,设定目标减震比为0.6,通过优化计算程序,求得 SPIS ⁃Ⅱ惯容系统的参数值如下:刚度比κ=0.45,惯质比μ=0.65,名义阻尼比ξ=0.08。
3.2 地震动选取
根据文献[17⁃18],从 PEER 数据库中选取普通地震动及两类长周期地震动(包括近场脉冲地震动与远场类谐和地震动)各3条。对于不同地震动,其选波步骤如下:(1)采用地震动加速度谱平均周期 Tr 与 PGV/PGA 值作为普通地震动与长周期地震动的区分依据,当 Tr >2 s 且 PGV/PGA>0.2时为长周期地震动,反之为普通地震动。(2)采用断层距Rrup及地震动尾波段与原始波的速度谱比值λTp作为近场脉冲地震动与远场类谐和地震动的区分依据,Rrup<20 km 且λTp<0.8的为近场脉冲地震动,而Rrup>60 km 且速度谱比值λTp>0.8的为远场类谐和地震动。采用SeismoSignal软件对地震动进行处理,得到三种地震动的平均反应谱曲线,如图7所示。
所选取的地震动基本参数如表4所示。并在3类地震动中各选取一条波,对其傅里叶谱、能量谱进行分析。由图8可得,普通地震动的傅里叶谱及能量谱分布较为均匀,而长周期地震动的傅里叶谱及能量谱主要集中在低频分段,说明长周期地震动的低频分量较为丰富。此外,长周期地震动的能量谱幅值大于普通地震动的幅值,说明在发生地震时长周期地震动向结构输送的能量大于普通地震动,将会对结构产生更为不利的影响。
3.3 时程分析
3.3.1 隔震层位移
根据《建筑抗震设计规范》[19],隔震支座的极限水平位移可达0.55D 和3t 中的较小值(D 为隔震橡胶支座有效直径,t 为支座橡胶层总厚度),结合结构模型,其隔震支座水平位移限值为275 mm 。为直观地表示惯容系统对層间隔震结构的控制作用,定义减震率如下:
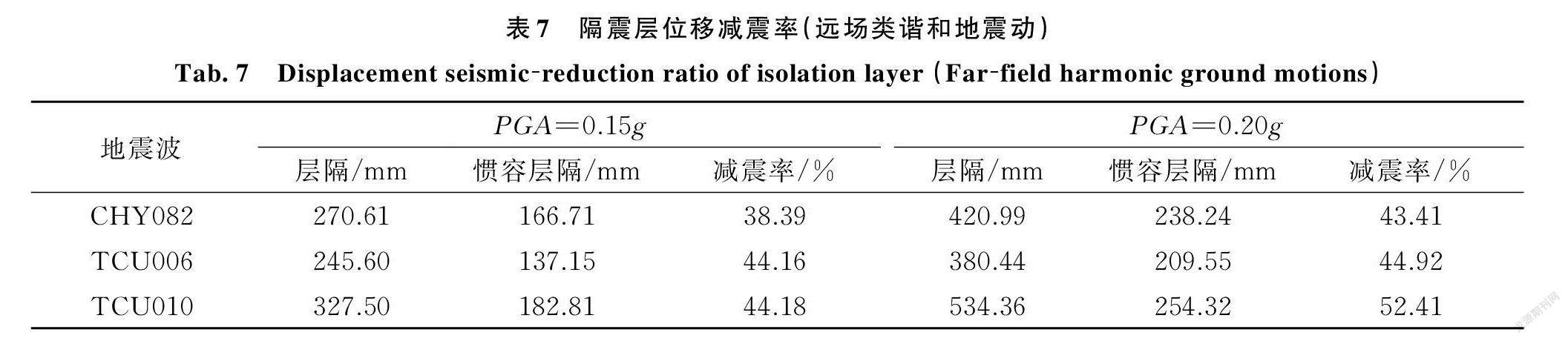
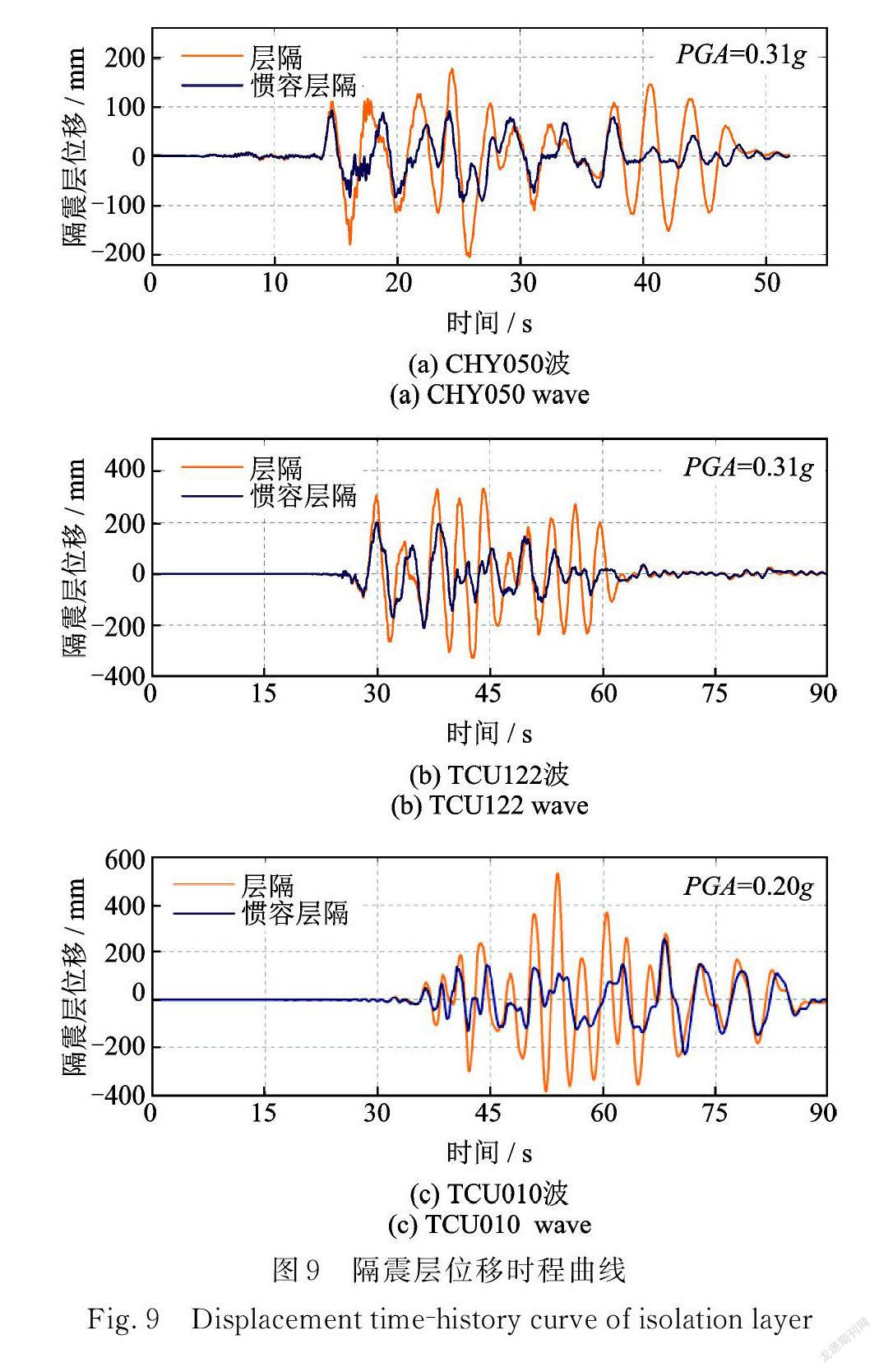
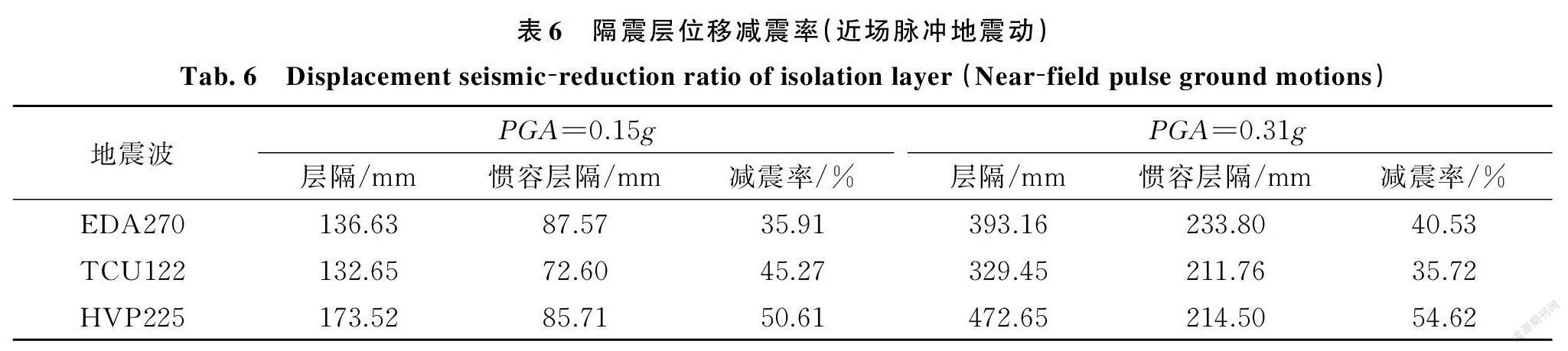
为研究惯容系统对层间隔震结构的减震作用,对惯容⁃层间隔震结构进行时程分析。表5~7给出了不同地震动作用下隔震层的位移减震率,图9给出了罕遇地震下隔震层的位移时程曲线。因远场类谐和地震动低幅值的特性,故将其最大幅值仅调至0.20g[16]。
分析表5~7及图10可得:在隔震层加入惯容系统后,长周期地震作用下,隔震层的最大位移得到了有效的控制,变形值控制在隔震橡胶支座的容许变形值之内。在普通地震动与长周期地震动作用下的隔震层位移减震率均在40%左右,与设定的目标减震比接近,说明在不同地震动作用下,惯容系统可较好地控制隔震层的位移,发挥其良好的减震效果。
随着地震动幅值的增大,惯容系统的减震效果增强,部分地震动作用下隔震层位移减震率达50%以上,有效地控制了隔震层的位移,使结构的安全性能得到保障。
3.3.2 层间位移响应
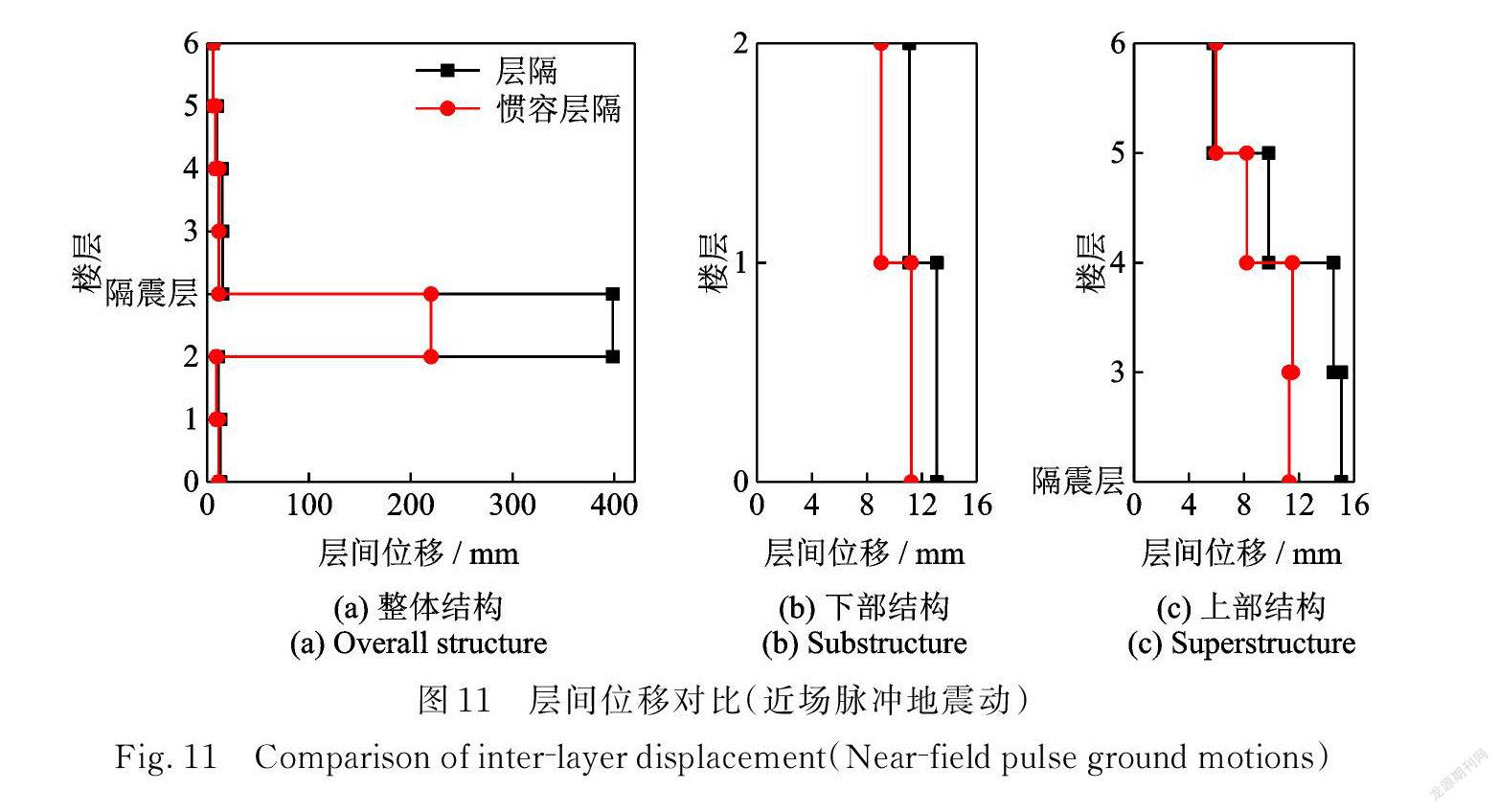
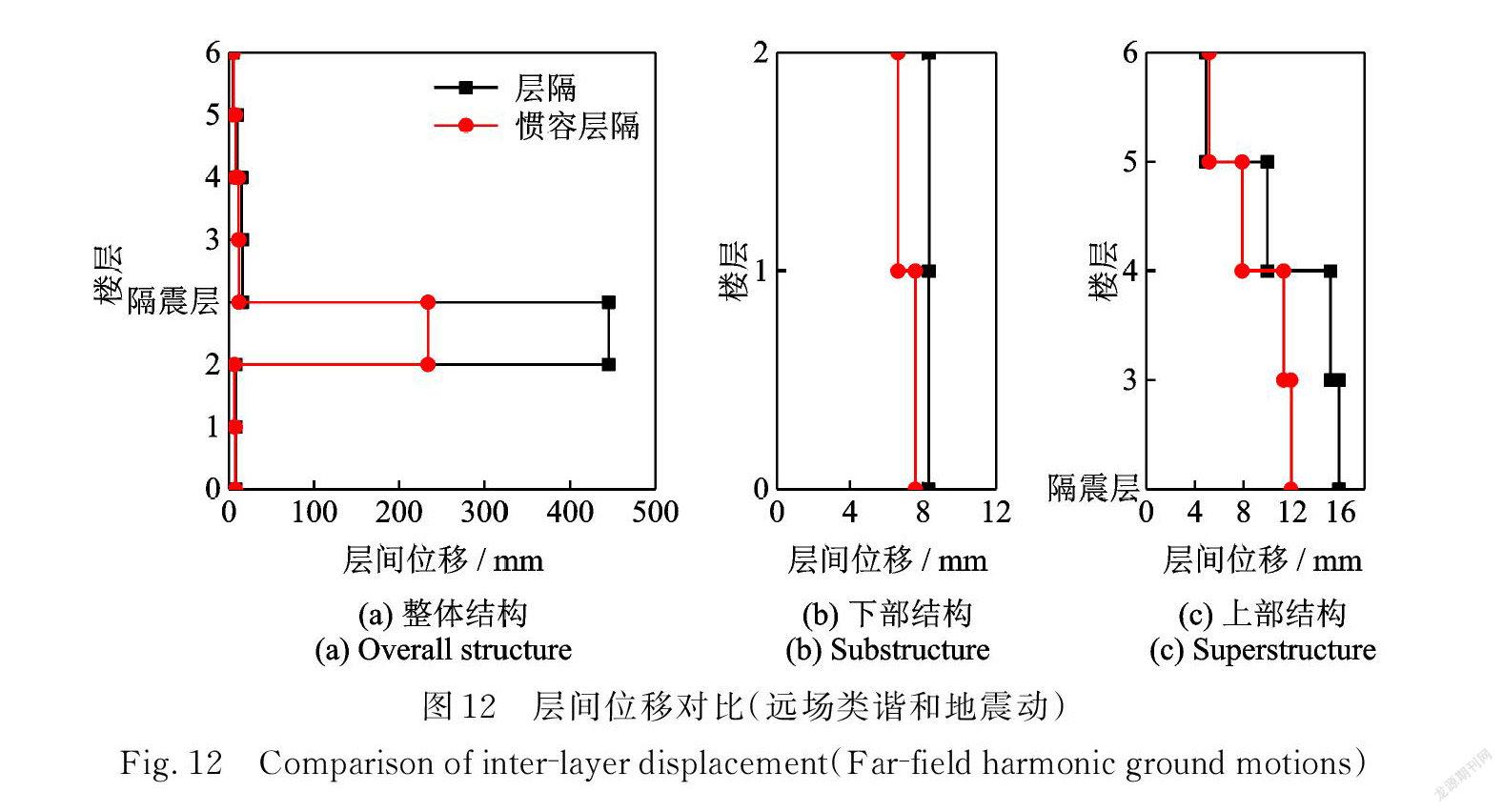
图10~12给出了不同地震动作用下,层间隔震结构与惯容⁃层间隔震结构的层间位移均值响应。
分析图10~12可得:在隔震层加入惯容系统不仅可有效控制隔震层的位移,同时可进一步控制隔震层上、下部结构的层间位移。对比三类地震动,可以观察到,在长周期地震动作用下,惯容系统对上部结构的控制效果更为显著。
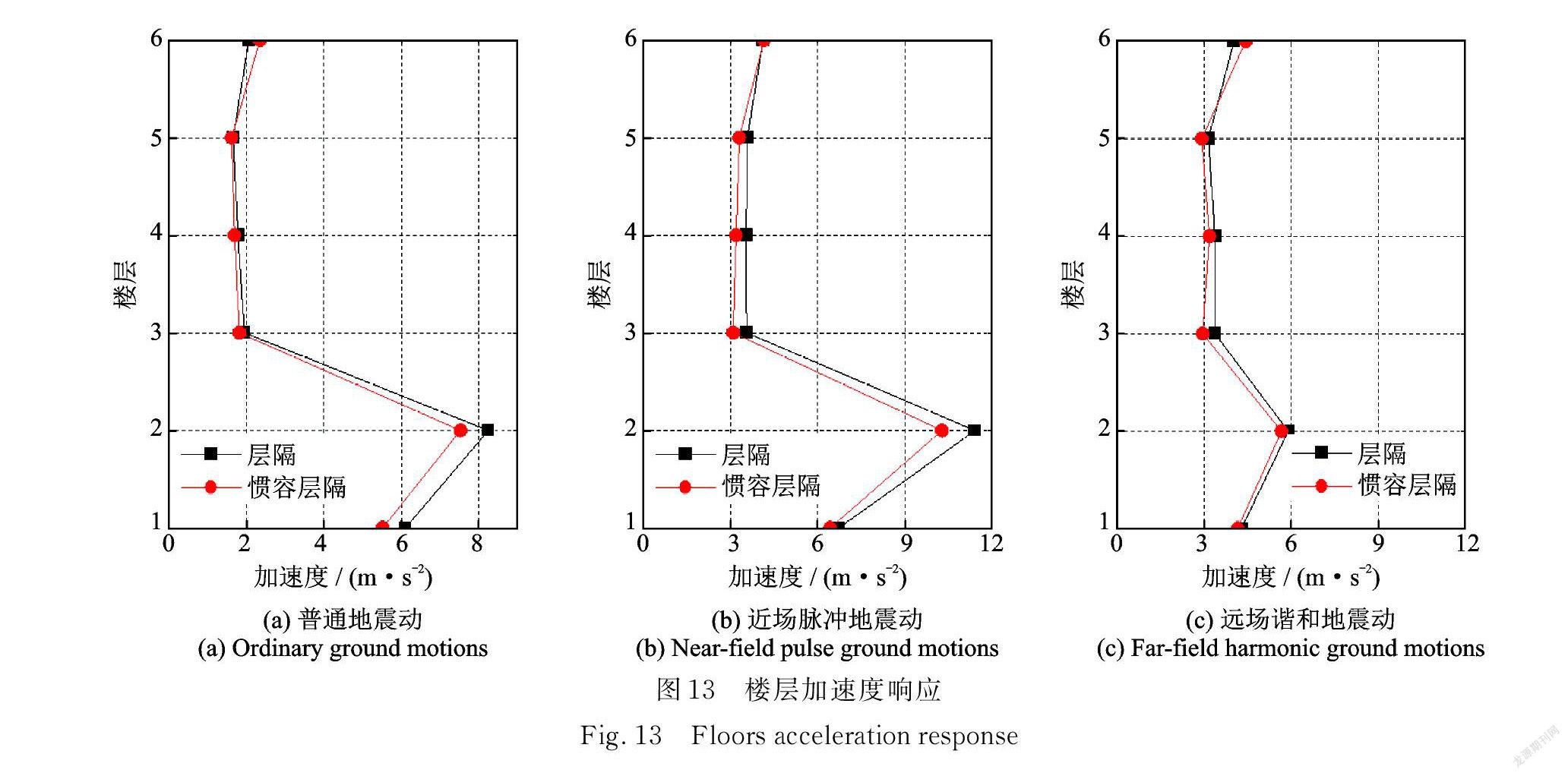
3.3.3 楼层加速度响应
图13给出了不同地震动作用下,层间隔震结构与惯容⁃层间隔震结构的楼层加速度响应。分析可得,在隔震层中加入惯容系统后,各楼层的加速度响应与层间隔震结构相近,但顶层的加速度响应略有增大,这与惯容系统出力大小有关,分析认为可以通过降低隔震层位移减震率的方法来提高惯容系统对楼层加速度响应的控制。
3.3.4 基底剪力响应
表8~10给出了不同地震作用下层间隔震结构及惯容⁃层间隔震结构的基底剪力和相应的减震率。图14给出了地震动 CHY050波,TCU122波及 TCU010波作用下结构基底剪力时程曲线。
由表8~10及图14可得,在不同地震动作用下,相较于层间隔震结构,在隔震层加入惯容系统后,结构基底剪力均得到进一步控制,其减震率在0~20%之间,说明在参数设计过程中虽未将下部子结构动力响应作为优化目标,但能降低结构基底剪力。
3.4 惯容参数有效性分析
为进一步验证3.1节 SPIS ⁃Ⅱ惯容系统的参数的有效性,本节将惯质比μ设为常量,设定3.1节计算所得最优刚度比为κ opt ,最优名义阻尼比为ξopt,研究刚度比κ与名义阻尼比ξ二者发生偏差时(如表11所示),惯容层间隔震结构的减震效果。
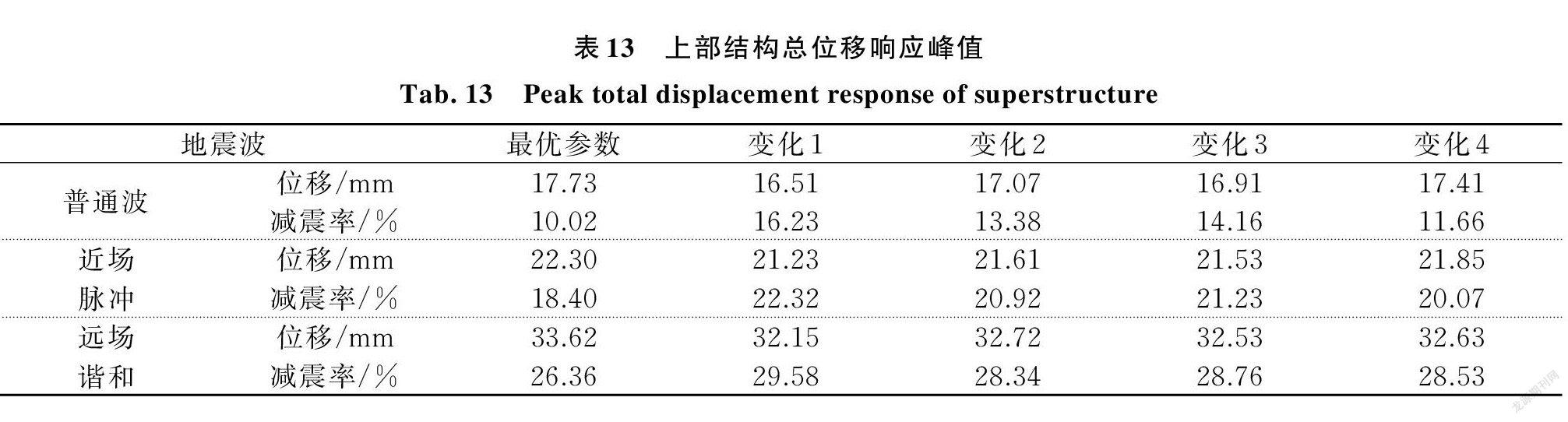
表12,13给出了惯容系统系统参数变化时隔震层位移及上部结构总位移变化情况。分析表12,13可得,当优化参数发生偏差时,可能造成隔震层位移减震率降低,但此时上部结构总位移的减震率却有所增大。这种现象与2.2节得出的结论一致,即与上部结构总位移及隔震层位移不可能同时最小化的结论相吻合。
4 结论
(1)提出的惯容系统参数优化设计方法可便捷有效地确定惯容系统参数,并达到预期性能目标。采用虚拟激励法求解结构的随机振动响应,并利用随机振动响应结果进行参数设计,确定最终参数设计方案,该方法大大简化了参数设计过程的计算量,提高了参数设计的效率。
(2)SPIS⁃Ⅱ惯容层间隔震系统可有效减小隔震层位移。位移减震率平均值达40%以上,且随着地震动幅值的增大,惯容系统对隔震层位移的减震
效果加强,可以有效解决长周期地震动作用下层间隔震结构隔震层位移超限的问题。
(3)SPIS⁃Ⅱ惯容系统在控制隔震层位移响应的同时,也进一步减小了下部子结构的位移响应和基底剪力。
参考文献:
[1] 杨奎,谭平,陈华霆,等.大底盘层间隔震结构一体化设计方法研究[ J ].廣州大学学报(自然科学版),2020,19(6):77-86.
YANG Kui,TAN Ping ,CHEN Huating,et al . Re ⁃ search on integrated design method of large base inter- story isolation structure[ J ]. Journal of Guangzhou Uni⁃ versity (Natural Science Edition),2020,19(6):77-86.
[2] PARK S,GHASEMI H,SHEN J,et al . Simulation ofthe seismic performance of the Bolu Viaduct subjected to near-fault ground motions [ J ]. Earthquake Engineering and Structural Dynamics,2004,33:1249-1270.
[3] 吴应雄,颜桂云,石文龙,等.长周期地震动作用下高层隔震结构减震性能试验研究[ J ].振动工程学报,2017,30(5):806-816.
WU Yingxiong,YAN Guiyun,SHI Wenlong,et al . Experimental study on the seismic reduction perfor⁃ mance of high-rise isolated structure under long-period ground motions [ J ]. Journal of Vibration Engineering,2017,30(5):806-816.
[4] 王亚楠,李慧,杜永峰. TMD-基础隔震混合控制体系在近场地震作用下的能量响应与减震效果分析[ J ].振动与冲击,2014,33(4):204-209.
WANG Yanan, LI Hui , DU Yongfeng . Energy re⁃ sponse and anti-vibration effect analysis for a base-isolat⁃ ed structure with TMD under near-field earthquake[ J ]. Journal of Vibration and Shock,2014,33(4):204-209.
[5] Lazar I F ,Neild S A ,Wagg D J . Using aninerter-based device for structural vibration suppression [ J ]. Earthquake Engineering and Structural Dynamics,2014,43(8):1129-1147.
[6] Saitoh M . On the performance of gyro-mass devices fordisplacement mitigation in base isolation systems [ J ]. Structural Control and Health Monitoring ,2012, 19(2):246-259.
[7] 王云骞,唐和生.惯性减振和基础隔震混合控制研究[ J ].建筑结构,2017,47(S2):321-324.
WANG Yunqian,TANG Hesheng . Research on the hy⁃ brid control of inertia vibration absorber and base isola⁃ tion[ J ]. Building Structure,2017,47(S2):321-324.
[8] 张瑞甫,吴明瑞,周方圆,等.利用惯容隔震系统的结构层间隔震研究[ J ].世界地震工程,2020,36(4):8-16. ZHANG Ruifu,WU Mingrui,ZHOU Fangyuan,et al . Research on mid-story isolation of structure using inert⁃ er isolation system [ J ]. World Earthquake Engineering,2020,36(4):8-16.
[9] ZHAO Zhipeng,ZHANG Ruifu,JIANG Yiyao,et al .Seismic Response mitigation of structures with a friction pendulum inerter system [ J ]. Engineering Structures,2019,193:110-120.
[10] QIAN Feng,LUO Yifan,SUN Hongxin,et al . Opti⁃mal tuned inerter dampers for performance enhancement of vibration isolation[ J ]. Engineering Structures,2019,198:109464.
[11]葉昆,舒率.基于性能需求的基础隔震结构附加调谐惯容阻尼器的优化设计研究[ J ].动力学与控制学报,2020,18(5):57-62.
YE Kun,SHU Shuai . Optimal design of base-isolated structure with supplemental tuned inerter damper based on performance requirement [ J ]. Journal of Dynamics and Control,2020,18(5):57-62.
[12] PAN Chao,ZHANG Ruifu . Design of structure with in⁃erter system based on stochastic response mitigation ra⁃ tio [ J ]. Structural Control and Health Monitoring,2018,25(6):e2169.
[13] ZHANG R F,ZHANG L Q,PAN C,et al . Targetedmodal response control of structures using inter-based systems based on master oscillator principle[ J ]. Interna ⁃ tional Journal of Mechanical Sciences , 2021, 206:106636.
[14] LIU Yanhui,WU Jinbiao,MARCO Dona . Effective ⁃ness of fluid-viscous dampers for improved seismic per⁃ formance of inter-story isolated buildings[ J ]. Engineer⁃ ing Structures,2018,169:276-292.
[15] LI Chunxiang CHANG Ke,CAO Liyuan,et al . Perfor⁃mance of a nonlinear hybrid base isolation system under the ground motions[ J ]. Soil Dynamics and Earthquake Engineering,2021,143:106589.
[16] Kalpakidis I V . Effects of heating and load history on thebehavior of lead-rubber bearings[ D ]. Buffalo:Universi⁃ ty at Buffalo,the State University of New York,2008.
[17]许立英,刘宁,吴应雄.基于抗震分析的长周期地震动的界定与选取[ J ].地震研究,2019,42(4):569-578.
XU Liying,LIU Ning,WU Yingxiong . Definition and selection of long-period ground motion based on the anti- seismic analysis[ J ]. Journal of Seismological Research,2019,42(4):569-578.
[18]刘烁宇,李英民,戴明辉.盆地场地远场长周期地震动输入的确定[ J ].建筑结构学报,2018,39(8):110-118.
LIU Shuoyu,LI Yingmin,DAI Minghui . Determina ⁃ tion of far-field long-period ground motion input in basin[ J ]. Journal of Building Structures , 2018, 39(8):110-118.
[19]建筑抗震设计规范:GB50011—2010(2016修订)[S].北京:中国建筑工业出版社,2016.
Code for seismic design of building :GB50011—2010(2016 Revision)[S]. Beijing:China Building Industry Press,2016.
Seismic response analysis of inerter -inter-storey isolated structure under long -period ground motions
WU Ying-xiong1,2,ZHENG Xiang-yu1,2,WENG Jin-hua3,WANG Lin-jian4,JIANG Li-ling3
(1.Department of Civil Engineering,Fuzhou University,Fuzhou 350108,China;
2.Fujian Provincial Key Laboratory on Multi-Disasters Prevention and Mitigation in Civil Engineering,Fuzhou 350108,China;
3.Fuzhou Architectural Design Institute Co .Ltd .,Fuzhou 350011,China;
4.Yunnan Institute of Earthquake Engineering,Kunming 650041,China)
Abstract: Previous studies have shown that the combination of inerter system and base isolation technology can reduce the dynamic response of base isolated structure under long-period ground motions . But the control effect of inerter system on inter-storeyisolat⁃ ed structure is different from that of base isolated structure,which needs further research . The SPIS-Ⅱinerter system is applied to the inter-storey isolated structure . The parameters of the inerter system are designed . The seismic-reduction effect of the inerter-in⁃ ter-storey isolated structure under long-period ground motions is studied by numerical analysis . The results show that using the vir⁃ tual excitation method to solve the random vibration response of the structure can quickly and effectively determine the parameters of the inertersystem . The inerter system greatly reduces the displacement of the isolation layer,effectively solves the problem of displacement overrun of the isolation layer under long-period ground motions,and the displacement seismic-reduction ratio increas? es with the increase of ground motion amplitude . The inerter-inter-storey isolated system not only controls the response of the su⁃ perstructure,but also further reduces the seismic response of the substructure .
Key words : inter-storey isolated structure;long-period ground motions;inerter system;displacement of isolation layer;displace⁃ ment seismic-reduction ratio
作者简介:吴应雄(1969—),男,博士,教授。电话:13950075100;E-mail:wyxfz2006@163.com。
通讯作者:翁锦华(1966—),男,硕士,教授级高级工程师。电话13328696169;E-mail:wengjinhua2003@sina .com。
