分数阶导数系统非平稳随机振动灵敏度分析的时域显式方法

冼剑华 苏成

摘要：分数阶导数模型是描述黏弹性材料本构关系的理想模型。进行了分数阶导数线性系统非平稳随机振动的灵敏度分析。建立分数阶导数系统动力响应的时域显式表达式；采用灵敏度分析的直接求导法或伴随变量法，推导系统动力响应灵敏度的时域显式表达式；提出分数阶导数系统响应统计矩灵敏度高效计算的时域显式方法。所提出的基于直接求导法和伴随变量法的时域显式方法，分别适用于少设计变量和多设计变量两种情况下的响应统计矩灵敏度分析。以非平稳地震激励下设置分数阶导数黏弹性阻尼器的层剪切结构为数值算例，验证了所提方法的计算精度和计算效率。

关键词：随机振动灵敏度；分数阶导数；时域显式方法；直接求导法；伴随变量法

中图分类号： O324；TU311.3    文献标志码： A    文章编号：1004-4523（2022）05-1058-10

DOI：10.16385/j .cnki .issn .1004-4523.2022.05.003

引言

理论和实验研究表明，分数阶导数模型能够同时模拟黏弹性材料的应力松弛特性和蠕变特性，是描述黏弹性材料本构关系的理想模型[1⁃2]。近年来，在结构振动领域，分数阶导数模型已被广泛用于描述黏弹性阻尼器的力学行为[3⁃5]。

分数阶导数系统的随机振动分析已引起了不少学者的关注。Spanos 和 Zeldin[6]提出了分数阶导数线性系统平稳随机振动的频域分析方法。Agraw ⁃ al[7]给出了分数阶导数单自由度线性系统平稳或非平稳随机振动的时域解析解答。Di Paola 等[8]基于 Lyapunov 矩方程法求解了分数阶导数线性振子的平稳或非平稳随机响应。上述研究属于线性随机振动分析范畴。在非线性随机振动分析方面，Spanos 和Evangelatos[9]利用蒙特卡罗模拟和统计线性化法分别求解了平稳白噪声激励下分数阶导数非线性振子的响应统计量。孙春艳和徐伟[10]借助随机平均法和统计线性化法，研究了分数阶导数单自由度非线性系统在平稳白噪声下的响应功率谱密度估计。 Xu 和 Li[11]采用概率密度演化法对设置分数阶导数黏弹性阻尼器的单自由度非线性随机结构进行了动力可靠度分析。更多关于分数阶导数系统随机振动分析的研究可参考文献[12⁃14]。

灵敏度分析是结构优化、模型修正和结构损伤识别等问题面临的重要课题。Kobelev[15]研究了分数阶导数线性非保守系统的失稳临界荷载灵敏度。 Martinez ⁃ Agirre和Elejabarrieta[16]求解了分数阶导数悬臂梁线性结构的特征值和特征向量灵敏度。 Lewandowski 和ŁaseckaPlura⁃[17]研究了设置分数阶导数黏弹性阻尼器线性结构的动力特性灵敏度。Li 等[18]和 Yun 等[19]对黏弹性阻尼线性系统进行了动力响应灵敏度分析，他们的方法同样适用于分数阶导数系统。上述研究仅考虑了分数阶导数线性系统动力特性或确定性动力响应的灵敏度，而针对分数阶导数系统随机振动灵敏度问题的研究目前尚未见到有文献报道。另一方面，黏性阻尼线性系统随机振动灵敏度问题的研究则相对成熟，相关研究可参考文献[20⁃21]。

近年来提出的一类非平稳随机振动时域显式方法[22⁃25]，通过构建结构动力响应及其灵敏度的时域显式表达式，能够在时域内直接建立非平稳响应统计矩及其灵敏度的显式列式，实现任意时刻和自由度的降维计算，并应用于非平稳随机激励下的结构拓扑优化，具有理想的计算精度和计算效率。在上述研究的基础上，本文将时域显式方法进一步发展应用于分数阶导数线性系统的非平稳随机振动灵敏度分析。首先构建分数阶导数系统动力响应的时域显式表达式；进而采用灵敏度分析的直接求导法或伴随变量法，推导系统动力响应灵敏度的时域显式表达式；最终利用统计矩的运算规律，建立系统非平稳响应统计矩灵敏度的时域显式列式。以非平稳地震激励下设置分数阶导数黏弹性阻尼器的层剪切结构为数值算例，验证了所提方法的计算精度和计算效率。

1 分数阶导数系统动力响应时域显式表达式

分数阶导数多自由度线性系统的运动方程可以表达如下：

式中  M，C，K 和 Cα分别为质量矩阵、黏性阻尼矩阵、刚度矩阵和分数阶导数阻尼矩阵；U （ t ），U̇ （ t ）和 Ü （ t ）分别为位移向量、速度向量和加速度向量； D αtU （ t ）表示對位移向量 U （ t ）关于时间 t 求α（0≤α<1）阶导数；F （ t ）为非平稳随机激励；L 为随机激励定位向量。

分数阶导数的定义有很多种，其中最常用的有 Riemann ⁃ Liouville （ RL ）定义、Caputo （C）定义和Grunward ⁃ Letnikov （GL）定义。 GL 定义在数值计算中是最适用的，它可以表达为[26]：

式中Δ t 为时间步长；n 为时间步数；GLk为 GL 系数，它可以表达为[9]：

式中Γ（·）表示 Gamma 函数。利用 Gamma 函数的性质，GL 系数可以用如下递推关系式进行计算：

定义分数阶导数系统的状态向量如下：

采用 Newmark⁃β数值积分法求解式（1），能够推导得到系统状态向量的递推公式为（推导过程见附录）：

式中wk =（Δ t ）-αGLk （0≤ k ≤ n ）； Vi = V （ ti ），Vi -1= V （ ti -1），Vi - k = V （ ti - k ），Fi = F （ ti ），Fi -1= F （ ti -1），其中ti = iΔ t，ti -1=（ i -1）Δ t，ti - k =（ i - k ）Δt；Q 1，Q 2，T 和 T1只与结构参数有关，它们的表达式以及推导过程见附录。

不失一般性，假定 V0= V （0）=0和 F0= F （0）=0，基于式（6）能够推导得到系统状态向量的时域显式表达式为：

式中  F[ i ]=[ F 1  F2  … Fi ]T；Ai =[ Ai，1  Ai，2  … Ai，i ]，其中系数向量 Ai，j （1≤ j ≤i≤ n ）可以由以下闭合公式进行计算：

根据式（8）所揭示的系数向量之间的内在关系，仅系数向量 Ai，1（1≤i≤ n ）需要计算和存储，其余系数向量均可以用 Ai，1（1≤i≤ n ）表示。应当指出，系数向量 Ai，1具有明确的物理意义，它表示在 t1时刻作用的单位脉冲激励f （ t ）（如图1所示）下系统在ti时刻的状态向量。因此，系数向量 Ai，1（1≤i≤ n ）的计算量相当于对分数阶导数系统进行1次响应时程分析。

一般而言，人们只关注系统的某些关键响应，并不需要求出系统中所有的响应。假设ri为所关注的关键响应，如位移响应、速度响应、位移响应分数阶导数或构件内力响应等，则由式（7）能够得到关键响应ri的时域显式表达式为：

式中   a i（r）=[ a i（r），1  a i（r），2  …  a i（r），i ]，其中 a i（r），j = qT Ai，j （1≤ j ≤ i ≤ n ）；q =[ q D（T）   q V（T）   q α（T）]T 为转换向量，其中 qD，qV 和 q α分别为针对位移响应、速度响应和位移响应分数阶导数的转换向量。当ri为 Vi 中的某一位移响应、速度响应或位移响应分数阶导数时，q 中除与该位移响应、速度响应或位移响应分数阶导数对应的元素为1外，其余元素均为0。当ri为某一构件内力响应时，q 依赖于相应的本构关系。

2 基于直接求导法的动力响应灵敏度时域显式表达式

假设θ为分数阶导数系统中的一个设计参数，则对运动方程（1）两端同时关于参数θ求导能够得到以下灵敏度方程：

式中  ∂M ∂θ，∂ C ∂θ，∂K ∂θ，∂ Cα∂θ和∂L ∂θ分别为矩阵 M，C，K，Cα 和 L 关于参数θ的灵敏度；∂ U （ t ）∂θ，∂ U̇ （ t ）∂θ，∂ Ü （ t ）∂θ和∂D αtU （ t ）∂θ分别为响应向量 U（ t ），U̇ （ t ），Ü （ t ）和 DαtU （ t ）关于参数θ的灵敏度。

由式（10）可以看出，灵敏度方程的求解依赖于运动方程（1）的求解。由式（1）可将 Ü （ t ）表达为：

将式（11）代入式（10）可得：

式中  V （ t ）如式（5）所示；L 1和 L2可以表达为：

对比式（1）和式（12）可知，灵敏度方程和运动方程在形式上是一致的。因此，与式（6）类似，系统状态向量灵敏度的递推公式可以表达为：

假定系统的初始条件为 V0=0，并且初始条件与设计参数θ无关，即∂ V0∂θ=0，则基于式（6）和（14）能够推导得到系统状态向量灵敏度的时域显式表达式为：

式中 F[ i ]=[ F 1 F2 … Fi ]T；Bi =[ Bi，1 Bi，2 … Bi，i ]，其中系数向量 Bi，j （1≤ j ≤i≤ n ）可以由以下闭合公式进行计算：

式中：

与式（8）类似，式（16）同样揭示了系数向量 Bi，j （1≤ j ≤i≤ n ）之间的内在关系，仅 Bi，1（1≤i≤ n ）需要进行计算和存储，其余系数向量均可以用 Bi，1（1≤i≤ n ）表示。与 Ai，1类似，系数向量 Bi，1同样具有明确的物理意义，它表示在 t1时刻作用的单位脉冲激励f （ t ）（如图1所示）下，系统在ti时刻的状态向量灵敏度。因此，系数向量 Bi，1（1≤i≤ n ）的计算量相当于对分数阶导数系统进行1次响应灵敏度时程分析。

记式（9）中关键响应ri关于参数θ的灵敏度为∂ri ∂θ，则由式（15）可得∂ri ∂θ的时域显式表达式为：

式中   b i（r）=[ b i（r），1   b i（r），2  …  b i（r），i ]，其中 b i（r），j = qT Bi，j （1≤ j ≤ i ≤ n ）。

假设考虑 m 个设计参数，则基于直接求导法构建关键响应ri关于所有参数灵敏度的时域显式表达式，计算量相当于对分数阶导数系统进行 m 次响应灵敏度时程分析。当所涉及的设计参数数目较多时，上述方法计算量较大，此时可基于伴随变量法构建关键响应灵敏度的时域显式表达式。

3 基于伴随变量法的动力响应灵敏度时域显式表达式

设 r （ t（～））为所关注t（～）时刻的位移响应或构件内力响应，则响应 r （ t（～））可以表达为以下积分形式：

式中  td 为位移响应 U（ t ）的持续时长；qD为针对位移响应的转换向量；δ（·）为 Dirac 函数。

为了计算响应 r （ t（～））关于参数θ的灵敏度，引入一任意伴随向量λ（ t ），并定义一个新的变量ψ（ t（～））为：

由于運动方程（1）在任意时刻恒成立，ψ（ t（～））恒等于 r （ t（～）），所以它们关于参数θ的灵敏度也恒等，即：

对式（20）左右两端同时关于参数θ求导，并进行分部积分，整理后可得：

尽管式（22）对任意的伴随向量λ（ t ）都成立，但为了避免计算位移向量的灵敏度∂U （ t ）∂θ，可选择一伴随向量以消除其中含∂U （ t ）∂θ的积分项，得到以下伴随方程：

假定系统的初始位移和速度与设计参数θ无关，则有∂ U （0）∂θ=∂ U̇ （0）∂θ=0。同时，令式（22）的后三项均等于0，得到以下终值条件：

此时，式（23）和（24）组成一个关于伴随向量λ（ t ）的终值问题。为求解该问题，可采用变量代换 s = td - t 将终值问题转换成初值问题，即：

式中  P （ s ）=- qDδ（ s - s（～））表示在时刻 s = s（～）= td - t（～）作用的脉冲激励；伴随向量Λ（ s ）=λ（ td - s ）； D s（α）Λ（ s ）表示对Λ（ s ）关于 s 求α（0≤α<1）阶导数，可表达为：

对比伴随方程（25）和运动方程（1）可知两者在形式上是一致的，所以式（25）同样可以采用 New ⁃ mark⁃β数值积分法进行求解。一旦获得伴随向量Λ（ s ）=Λ（ td - t ）=λ（ t ）后，由式（21）和（22）即可得到响应 r （ t（～））的灵敏度为：

若关注时刻 t（～）= ti = iΔ t 的响应ri = r （ ti ）（1≤i≤ n ），为简单起见，可令 td = ti +1=（ i +1）Δ t，此时 P （ s ）表示在时刻 s =Δt作用的脉冲激励。假定 U （0）= U̇ （0）=0和 F（0）=0，由式（1）和（2）可知 Ü （ 0）=0和 D αtU （0）=0，又因为Λ（0）=0，所以式（27）可以采用梯形积分公式求解如下：

式中Λ i - k +1=Λ（ ti - k +1）（1≤ k ≤ i ≤ n ）。

由式（11）可知：

将式（29）代入式（28）可得：

式中  Vk =[ UkT   U̇ kT   D αtUkT ]T （1≤ k ≤ i ≤ n ）；L 1和 L2如式（13）所示。

由式（7）可得响应 Ui 的时域显式表达式为：

式中  A i（U）=[ A i，（U）1  A i，（U）2  …  A i，（U）i ]，其中 A i，（U）j 取自系数向量 Ai，j （1≤ j ≤ i ≤ n ）中相应于 Ui 的列向量。

将式（7）和（31）代入式（30）可得响应灵敏度∂ri ∂θ的时域显式表达式为：

式中  b i =[ b i，1   b i，2  …  b i，i ]，其中：

由式（8）所揭示的系数向量 Ai，j （1≤ j ≤i≤ n ）之间的内在关系，可将式（33）改写成：

从式（34）可以看出，仅系数 b（～） i（r），1（1≤i≤ n ）需要进行计算和存储，其余系数均可以用 b（～） i（r），1（1≤i≤ n ） 表示。在已获得系数向量 Ai，j （1≤ j ≤i≤ n ）的基础上，若求得伴随向量Λ（ s ），即可基于式（34）计算系数b（～） i（r），j （1≤ j ≤i≤ n ）并构建响应灵敏度∂ri ∂θ的时域显式表达式（32）。需要指出的是，基于伴随变量法构建响应ri关于不同参数灵敏度的时域显式表达式，只需要进行1次伴随方程求解，计算量相当于对分数阶导数系统进行1次响应时程分析。因此，当所涉及的设计参数数目较多时，采用伴随变量法构建响应灵敏度的时域显式表达式会比采用直接求导法具有更高的计算效率，而当所涉及的设计参数数目较少时，采用直接求导法会更加简单直接。

4 非平稳随机振动灵敏度分析的时域显式方法

基于关键响应ri的时域显式表达式（9），及其灵敏度∂ri ∂θ的时域显式表达式（18）或（32），利用统计矩的运算规律能够直接计算得到响应ri的均值μ ri和方差σri（2）关于参数θ的灵敏度为：

或

式中  F[ i ]的均值向量和协方差矩阵可以表达为：

式中μF （ t ）和 RF （ t，τ）分别为非平稳随机激励 F （ t ）的均值函数和自相关函数。

应当指出，式（35）～（38）为分数阶导数系统响应统计矩灵敏度的时域显式列式，它建立了系统响应统计量灵敏度与激励统计量之间的直接联系。式（35）和（36）可以称作基于直接求导法的时域显式方法，而式（37）和（38）可以称作基于伴随变量法的时域显式方法。

5 数值算例

以图2所示设置分数阶导数黏弹性阻尼器的层剪切结构为数值算例，验证本文所提出的非平稳随机振动灵敏度分析时域显式方法的计算精度和计算效率。该结构每一层的质量和刚度分别为 mi =1.8×104 kg 和 ki =8.9×105 kN m （1≤i≤ N ），其中 N 为结构层数，在本算例中取 N =20。采用瑞利阻尼模型，取结构第1阶和第20阶模态的阻尼比为ζ=0.05。结构每一层均布置1个黏弹性阻尼器，阻尼器与楼层的夹角均为η= arccos 0.8。所布置黏弹性阻尼器的阻尼力模型取为分数阶 Kelvin 模型[17]，即：

式中ud，i为第i个黏弹性阻尼器两端节点的轴向相对位移；kd，i和 cd，i分别为第i个黏弹性阻尼器的刚度系数和阻尼系数。在本算例中，取α=0.6，kd，i = kd =3×105 kN/m和cd，i = cd =2.5×105 kN⋅ sα/m （1≤i≤20）。

結构受零均值非平稳地震激励 F（ t ）的作用， F （ t ）取为均匀调制非平稳随机过程，即 F （ t ）= g （ t ） f（ t ）。g （ t ）为均匀调制函数，取为：

式中δ=0.18，ta =6 s，tb =18 s，tc =30 s 。f （ t ）为零均值平稳随机过程，其功率谱密度函数取为Kanai Tajimi谱⁃[27]，即：

式中ω g =15.708 rad/s，ζg =0.6，S0=0.005 m 2/s3。 f （ t ）的自相关函数可以表达为[28]：

式中：

相应地，F （ t ）的自相关函数可以表达为：

考虑各层黏弹性阻尼器的刚度系数和阻尼系数均同时变化，此时仅有2个设计参数，分别为kd和 cd。分别采用基于直接求导法（Direct Differentiation Method ，DDM）和伴随变量法 （Adjoint  Variable Method，AVM）的时域显式方法（Explicit Time⁃Do ⁃ main Method，ETDM）对图2所示层剪切结构进行非平稳随机振动灵敏度分析。同时，采用基于蒙特卡罗模拟（Monte⁃ Carlo Simulation，MCS）的有限差分法（Finite Difference Method，FDM）计算随机振动灵敏度的参考解，其中差分步长取为设计参数的0.2%变化量，MCS 的样本数取为104。时程分析步长取Δt =0.02 s，时程分析总长为 T =30 s 。三种计算方法下结构顶层水平位移标准差关于kd和 cd 的灵敏度结果分别如图3和4所示。从图中可以看出，基于 DDM 的 ETDM 和基于 AVM 的 ETDM 计算结果基本重合，且均与基于 MCS 的 FDM 计算结果吻合良好，说明所提方法具有理想的计算精度。此外，从图3和图4还可以看出，顶层水平位移标准差灵敏度时程的变化趋势明显受到式（42）所示均匀调制函数的影响，说明在非平稳随机激励下分数阶导数系统的随机响应灵敏度具有明显的非平稳特征。

上述三种方法的计算时间如表1所示。从表中可以看出，在设计参数只有2个的情况下，基于 DDM 的 ETDM 和基于 AVM 的 ETDM 计算时间分别为2.3和2.1 s，均远少于基于 MCS 的 FDM 计算时间，说明所提方法具有理想的计算效率。这是因为在基于 MCS 的 FDM 中，需要对分数阶导数系统进行大量的响应时程分析。而在 ETDM 中，若基于DDM 构建响应灵敏度的时域显式表达式，计算量仅相当于对分数阶导数系统进行2次响应灵敏度时程分析；若基于 AVM 构建响应灵敏度的时域显式表达式，只需要进行1次伴随方程求解，计算量相当于对分数阶导数系统进行1次响应时程分析。

为了进一步考察所提方法在设计参数数目较多时的计算效率，考虑各层黏弹性阻尼器的刚度系数和阻尼系数各自不同变化，此时设计参数为kd，i和 cd，i （1≤i≤20），共计40个。采用基于 DDM 的 ET ⁃ DM 和基于 AVM 的 ETDM 分别计算顶层水平位移标准差最大值关于刚度系数kd，i和阻尼系数 cd，i （1≤i≤20）的灵敏度，计算结果分别如图5和6所示。从图5和6可以看出，上述两种方法的计算结果基本重合，这与图3和4所观察到的现象一致，同时还可以看出顶层水平位移标准差的最大值对底层黏弹性阻尼器刚度系数和阻尼系数的变化更敏感。

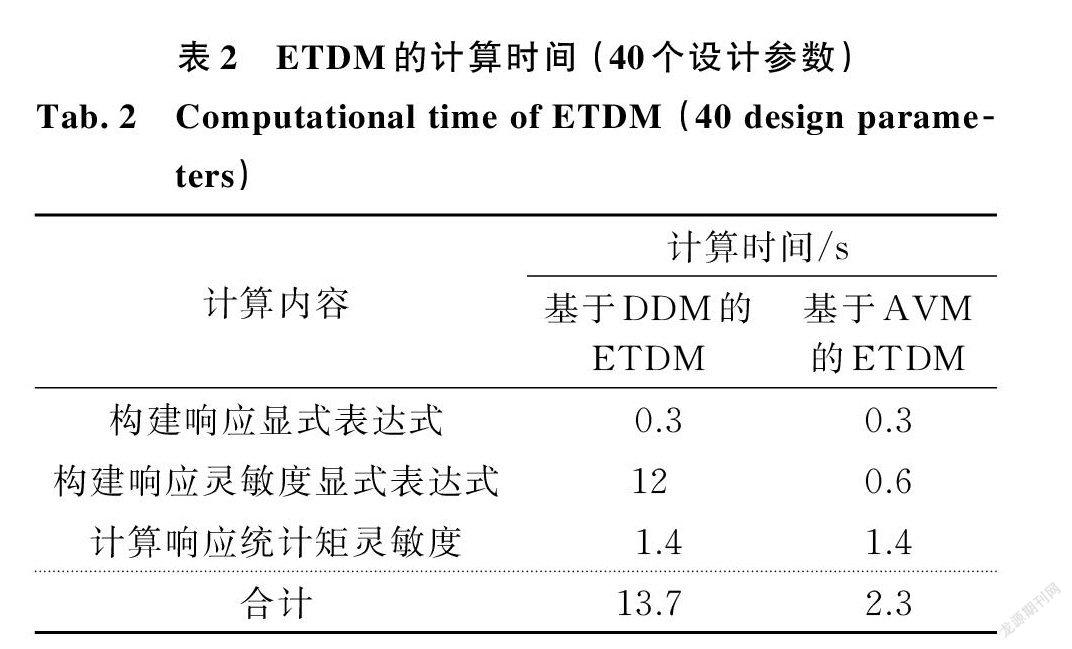
两种方法的计算时间如表2所示。从表中可以看出，当考虑40个设计参数时，基于 AVM 的 ET ⁃ DM 相比基于 DDM 的 ETDM 具有明显的效率优势。这是因为在 ETDM 中，若基于 DDM 构建响应灵敏度的时域显式表达式，计算量相当于对分数阶导数系统进行40次响应灵敏度时程分析；而基于 AVM 构建响应灵敏度的时域显式表達式，则只需要进行1次伴随方程求解，计算量相当于对分数阶导数系统进行1次响应时程分析。

应当指出，本文所提方法还可以进一步应用于分数阶导数系统非平稳随机振动优化设计中。特别地，当考虑分数阶黏弹性阻尼器性能参数优化时，由于所涉及的设计参数数目通常较少，可以采用基于 DDM 的 ETDM 进行灵敏度计算；当考虑分数阶黏弹性阻尼器布局拓扑优化时，由于所涉及的设计参数数目通常较多，可以采用基于 AVM 的 ETDM 进行灵敏度计算。

6 结论

基于灵敏度分析的直接求导法和伴随变量法，分别推导了分数阶导数线性系统动力响应灵敏度的时域显式表达式，提出了系统非平稳随机振动灵敏度分析的时域显式方法，可快速获取系统关键响应统计矩的灵敏度。数值算例结果表明，所提出的基于直接求导法或伴随变量法的时域显式方法具有理想的计算精度和计算效率。当设计参数数目较少时，采用基于直接求导法的时域显式方法更加简单直接；当设计参数数目较多时，采用基于伴随变量法的时域显式方法计算效率更高。本文所提方法可与非线性随机振动等效线性化法结合，用以求解分数阶导数非线性系统的非平稳随机振动灵敏度问题，有待进一步研究。

参考文献：

[1]  Bagley R L，Torvik P J . A theoretical basis for the ap⁃plication of fractional calculus to viscoelasticity[ J ]. Jour⁃ nal of Rheology，1983，27（3）：201-210.

[2]  Di Paola  M ，Pirrotta  A，Valenza  A . Visco-elastic be⁃havior through fractional calculus：an easier method for best fitting experimental results[ J ]. Mechanics of Mate ⁃ rials，2011，43（12）：799-806.

[3]  Makris  N ， Constantinou  M  C . Fractional  derivativeMaxwell  model  for  viscous  dampers [ J ]. Journal  of Structural Engineering，1991，117（9）：2708-2724.

[4]  Shen K L，Soong T T . Modeling of viscoelastic damp⁃ers for structural applications[ J ]. Journal of Engineering Mechanics，1995，121（6）：694-701.

[5]  Lewandowski R，Pawlak Z . Dynamic analysis of frameswith viscoelastic dampers modelled by rheological mod⁃ els with fractional derivatives[ J ]. Journal of Sound and Vibration，2011，330（5）：923-936.

[6]  Spanos P D，Zeldin B A . Random vibration of systemswith frequency-dependent parameters or fractional deriv⁃ atives [ J ]. Journal  of  Engineering  Mechanics ， 1997，123：290-292.

[7]  Agrawal  O  P . Stochastic  analysis  of dynamic  systemscontaining  fractional  derivatives [ J ]. Journal  of  Sound and Vibration，2001，247（5）：927-938.

[8]  Di Paola M，Failla G，Pirrotta A . Stationary and non-stationary  stochastic response  of linear  fractional visco? elastic  systems [ J ]. Probabilistic  Engineering  Mechan⁃ ics，2012，28：85-90.

[9]  Spanos P D，Evangelatos G I . Response of a non-linearsystem  with restoring  forces governed by  fractional de⁃ rivatives-time domain simulation and statistical lineariza⁃ tion  solution[ J ]. Soil  Dynamics  and  Earthquake  Engi⁃ neering，2010，30（9）：811-821.

[10]孙春艳，徐伟.分数阶导数阻尼下非线性随机振动结构响应的功率谱密度估计[ J ].应用力学学报，2013，30（3）：401-405.

Sun C Y，Xu W . Response power spectral density esti⁃ mate  of  a  fractionally  damped  nonlinear  oscillator [ J ].Chinese Journal of Applied Mechanics ，2013，30（3）：401-405.

[11] Xu J，Li J . Stochastic dynamic response  and reliabilityassessment of controlled structures with fractional deriv⁃ ative model of viscoelastic dampers[ J ]. Mechanical Sys⁃ tems and Signal Processing，2016，72-73：865-896

[12] Huang Z L，Jin X L，Lim C W，et al . Statistical analy⁃sis for stochastic systems including fractional derivatives [ J ]. Nonlinear Dynamics，2010，59（1-2）：339-349.

[13]李伟，赵俊锋，李瑞红，等. Guass白噪声激励下分数阶导数系统的非平稳响应[ J ].应用数学和力学，2014，35（1）：63-70.

Li  W ，Zhao  J  F ，Li  R  H ，et  al . Non-stationary  re⁃ sponse  of a  stochastic  system  with  fractional derivative damping under Gaussian white-noise excitation[ J ]. Ap⁃ plied Mathematics and Mechanics，2014，35（1）：63-70.

[14] Fragkoulis  V  C ，Kougioumtzoglou  I  A ，Pantelous  AA，et al . Non-stationary response statistics of nonlinear oscillators with fractional derivative elements under evo⁃ lutionary stochastic excitation[ J ]. Nonlinear Dynamics，2019，97：2291-2303.

[15] KobelevV . Sensitivity analysis of the linear nonconser⁃vative  systems  with  fractional  damping [ J ]. Structural and  Multidisciplinary  Optimization ， 2007， 33（3）：179-188.

[16] Martinez-Agirre M，Elejabarrieta M J . Higher order ei⁃gensensitivities-based numerical method for the harmon⁃ ic analysis of viscoelastically damped structures[ J ]. In ⁃ ternational Journal for Numerical Methods in Engineer⁃ ing，2011，88（12）：1280-1296.

[17] Lewandowski  R ，Łasecka-Plura  M . Design  sensitivityanalysis  of  structures  with  viscoelastic  dampers [ J ]. Computers and Structures，2016，164（1）：95-107.

[18] Li L，Hu Y J，Wang X L . Design sensitivity analysis ofdynamic response of nonviscously damped systems[ J ]. Mechanical  Systems  and  Signal  Processing ，2013，41（1-2）：613-638.

[19] Yun  K  S ，Youn  S  K . Design  sensitivity  analysis  fortransient  response  of  non-viscously  damped  dynamic systems[ J ]. Structural  and  Multidisciplinary  Optimiza? tion，2017，55（6）：2197-2210.

[20] Zhu M，Yang Y，Guest J K，et al . Topology optimiza⁃tion  for  linear  stationary  stochastic  dynamics ：applica⁃ tions  to  frame  structures [ J ]. Structural  Safety ，2017，67：116-131.

[21] Gomez F，Spencer B F . Topology optimization frame⁃work for structures subjected to stationary stochastic dy⁃ namicloads[ J ]. Structural and Multidisciplinary Optimi⁃ zation，2019，59：813-833.

[22]苏成，徐瑞.非平稳随机激励下结构体系动力可靠度时域解法[ J ].力学学报，2010，42（3）：512-520.

Su C，Xu R . Time-domain method for dynamic reliabili⁃ ty of structural systems subjected to non-stationary ran⁃ domexcitations[ J ]. Chinese Journal of Theoretical and Applied Mechanics，2010，42（3）：512-520.

[23] Su C，Xu R . Random vibration analysis of structures bya time-domain explicit formulation method[ J ]. Structur⁃ al Engineering and Mechanics，2014，52（2）：239-260.

[24] Hu Z Q，Su C，Chen T C，et al . An explicit time-do⁃main  approach  for  sensitivity  analysis  of non-stationary random vibration problems[ J ]. Journal of Sound and Vi⁃ bration，2016，382：122-139.

[25] Hu  Z  Q ，Wang  Z  Q ，Su  C ，et  al . Reliability  basedstructural topology optimization considering non-station⁃ ary stochastic excitations[ J ]. KSCE Journal of Civil En ⁃ gineering，2018，22（3）：993-1001.

[26] PodlubnyI . Fractional Differential Equations：An Intro ⁃duction  to  Fractional  Derivatives ， Fractional  Equa⁃ tions，to Methods of Their Solution and Some of TheirApplications[M]. New York：Academic Press，1999.

[27] Kanai K . Semi-empirical formula for the seismic charac⁃teristics  of  the  ground [ J ]. Bulletin  of  the  Earthquake Research Institute，1957，35（2）：309-325.

[28] Sun  G  J ，Li H  J . Stationary  models  of random  earth⁃quake ground motion and their statistical properties[ J ]. Earthquake  Engineering  and  Engineering  Vibration，2004，24（6）：21-26.

[29] Newmark N W . A method of computation for structuraldynamics [ J ]. Journal of the Engineering Mechanics Di⁃ vision，1959，85（7）：67-94.

Explicit time -domain method for sensitivity analysis of nonstationary random vibration of systems with fractional derivatives

XIAN Jian‑hua1，SU Cheng1，2

（1.School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510640，China；

2.State Key Laboratory of Subtropical Building Science，South China University of Technology，Guangzhou 510640，China）

Abstract： Fractional derivative models are capable of describing the constitutive behaviors of viscoelastic materials . This paper is devoted to the sensitivity analysis of nonstationary random vibration of linear systems comprising fractional derivative terms . The explicit time-domain expressions of dynamic responses are firstly established for the system with fractional derivatives . The sensitiv ? ities of dynamic responses are then derived using the direct differentiation method （DDM） or the adjoint variable method （AVM）. On the basis of the explicit expressions of dynamic responses and their sensitivities，an explicit time-domain method （ETDM） is proposed for efficient calculation of the sensitivities of statistical moments of responses . The proposed DDM- and AVM-based ET ⁃ DM are applicable to the scenarios with less and more design variables，respectively . A numerical example involving a shear-type structure under nonstationary seismic excitations and with viscoelastic dampers modelled by fractional derivatives is presented to validate the computational accuracy and efficiency of the proposed method .

Key words ： sensitivity of random vibration；fractional derivative；explicit time-domain method；direct differentiation method；ad⁃ joint variable method

作者简介：冼剑华（1994—），男，博士研究生。电话：13570433950；Email：jianhua .xian@qq .com。

通讯作者：苏成（1968—），男，博士，教授。电话：（020）87111636；Email：cvchsu@scut .edu .cn。

附录：公式（6）的推导过程

由式（1）可得ti时刻的运动方程为：

式中 D αtUi 可由式（2）得到：

Newmark⁃β数值积分法采用以下两个基本假定[29]：

式中：

式中γ和β为与积分稳定性有关的参数，本文取γ=0.5，β=0.25。

将式（A2）～（A4）代入式（A1）可得：

由式（A6）可得：

式中：

由式（A1）可得 Ü i为：

Ü i -1也可以类似表达为：

将式（A10）代入式（A7）可得：

式中：

将式（A10）和（A11）代入式（A4）可得：

式中

式中：

将式（A11），（A13）和（A15）合并可得式（6），式中：