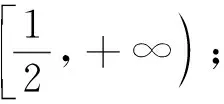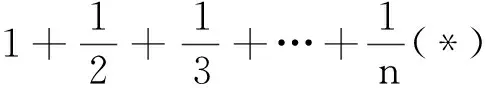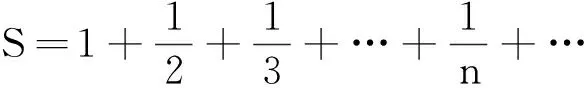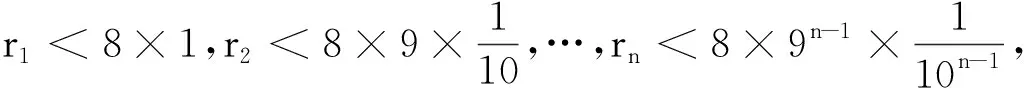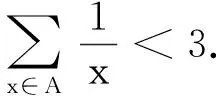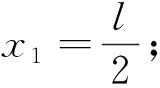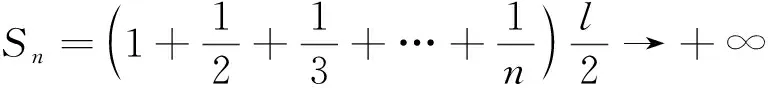与调和级数有关的几个数理问题赏析*
2022-11-14韦燕平
韦燕平
(江苏省无锡市第一中学 214000)
谢广喜
(江南大学理学院 214122)
一般地,我们将表达式a1+a2+a3+…+an+…称为无穷级数(简称级数),当无穷级数的极限存在时,称级数收敛(无穷等比数列各项和就是一个特殊的收敛级数),否则称级数发散.有关级数问题的深入研究主要在数学分析或复变函数论相关内容中有探讨,前者主要探讨实数背景下的数列敛散性问题,而后者主要探讨复数背景下的数列敛散性问题.

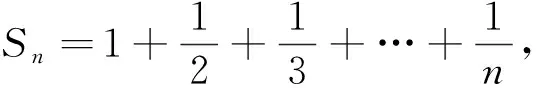
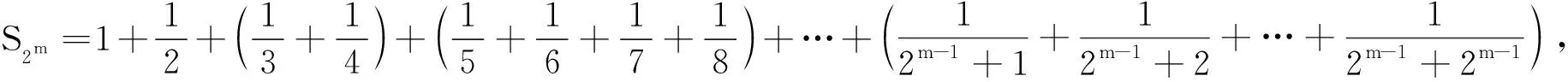
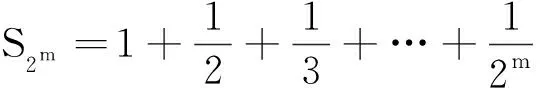

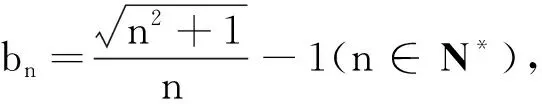
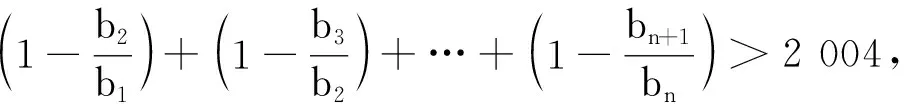
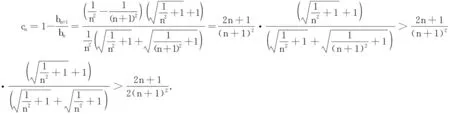




我们将证明,对于任意大于SN0的正整数m,必存在n>N0,使得Sn-m∈(a,b),也即m+a 为了与待证目标建立联系,我们令mi=[SN0]+i(i=1,2,3,…),利用(** )式,则mi>SN0,再利用(*)式,知存在ni,当ni>N0时,有mi+a 尽管调和级数本身是无法求和化简的,但我们还是可以找到适当的函数,动态描述其“下界”特性: (1)用a表示b,c; (2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围; 简解 (1)易得到b=a-1,c=-2a+1. 解析 为理解方便,我们下面具体针对不含数字9的情形予以证明(读者可以发现,我们的证明实际上与该数字具体是几是无关的).记r1=调和级数中不含数字9的1位(十进制)数的倒数之和(其中共有8项),r2=调和级数中不含数字9的2位(十进制)数的倒数之和(其中共有8×9项),r3=调和级数中不含数字9的3位(十进制)数的倒数之和(其中共有8×92项),…,rn=调和级数中不含数字9的n位(十进制)数的倒数之和(其中共有8×9n-1项;一般地,我们利用乘法原理可得到这个结果,首位由于不能为0,又不能为9,故有8种选法,其他各位有9种选法,故满足要求的n位(十进制)数共有8×9n-1个). 评注为了记忆简单方便,我们不妨称此为特殊前提下调和级数的反常收敛,当然,如果我们将个位数的部分放缩得精致一些(现在的放缩显然是比较粗糙的),则可得到更小一点的上界. 简解 与上题完全类似地,在k(k∈N*)位十进制正整数中,各位上的数码不含2,0,1,6者共有(10-4)k=6k个,其中首位分别为3,4,5,7,8,9的各有6k-1个,于是 图1 例5如图1所示,将若干块完全相同的均匀长方体砖块叠放起来,第一块砖相对于第二块砖最右端能伸出去的最大长度为x1;此时将1,2块砖看成一个整体,第二块砖相对于第三块砖最右端能伸出去的最大长度为x2;此时再将1,2,3块砖看成一个整体,记第三块砖相对于第四块砖最右端能伸出去的最大长度为x3……第n块砖相对于第(n+1)块砖最右端能伸出去的最大长度为xn,试求Sn=x1+x2+…+xn(设每块砖的长度为l). 图2