层次匿名群签名的概念与构建

程小刚， 郭韧， 周长利， 陈永红， 卢正添

(1. 华侨大学 计算机科学与技术学院， 福建 厦门 361021；2. 华侨大学 工商管理学院， 福建 泉州 362021)

群签名是一种具有中心地位的密码系统[1-2]，具有匿名和可追踪的良好特性，在电子投票[3-4]、电子货币[5-6]、电子拍卖[7-8]、可信计算[9-10]、车载互联网[11-13]和隐私保护[14]等领域应用广泛[15-16].群签名的概念是1991年由Chaum和Heyst提出的[1].1997年，Camenisch等[17]提出的CS97群签名方案，在群签名构建上具有十分重要的意义，其实现群公钥及签名的长度、签名和验证的计算复杂度都独立于群的大小，但其安全性基于随机预言模型(ROM).在标准模型下构建的群签名一般是利用两种签名方案，给群成员的证书为群管理员(GM)的签名，群成员利用此证书再生成群签名.GS08中提出的在标准模型下安全的、基于双线性群的高效非交互零知识证明方案，是第1种可对一大类关系进行零知识证明的方案.因此，GS08被广泛用于各种标准模型下安全群签名方案的构建[15].

把单位组织成层次结构的密码系统有一些相关工作，如基于身份的层次加密(HIBE)[18-20].由于基于身份的加密(IBE)系统中所有用户的私钥都由某个中心生成，负担较重，HIBE系统可由上层单位把下层单位的密匙生成工作委托给下层组织，如身份公钥Alice.hqu.edu.cn对应的私钥原来由中心生成，而在HIBE系统中此工作可由中心委托华侨大学来生成(即hqu.edu.cn负责生成所有*.hqu.edu.cn的私钥)，而华侨大学的私钥又可由教育部门来生成(即edu.cn负责生成所有*.edu.cn的私钥)，从而极大地降低了中心的负担.文献[21]中提出层次撤销群签名的概念，即在撤销时利用组织的层次结构进行灵活的撤销.层次群签名[22-23]可应用于匿名信用卡，在打开签名时，有多个被组织成层次结构的GM，签名者是树的叶子节点，GM可以打开签名，但每个GM只能打开本层.

传统群签名的匿名性只在本群内是匿名的，其匿名范围是不可变的.实现自主匿名群签名的简单做法是组织树中的每个单位生成自己的群签名方案，群成员向每个单位申请加入并获得相应的私钥，这样的缺点是没有实现单位的层次关系的限制.因此，本文提出一种匿名性可变的层次匿名群签名的概念，将成员所在的单位组织成层次架构，这样在生成群签名时可根据具体的应用自主选择匿名层次，这与层次撤销群签名在某种程度上是一种对偶关系；构建的方案能强制实现单位间的层次关系，即不属于本单位的成员不能加入与生成群签名.

1 初步知识

定义1层次匿名群签名由下列5个概率多项式算法构成.

1) 设置(Setup).GM将部门内所在单位组织成层次结构，叶子节点是人，即群成员，并生成层次结构中各单位的群公钥(GPK)和负责成员加入的群私钥(GSK).

2) 加入(Join).成员申请加入群，GM在核实其身份信息之后，可利用GSK生成其成员私钥(MSK)，用于生成群签名.

3) 签名(Sign).生成群签名时，成员可选择其匿名层次，即在从根到其叶子节点路径上任选一个单位，对应其群公钥，利用其MSK生成相应的群签名.

4) 验证(Verify).验证时，验证方能验证群签名的合法性(根据签名中包含的单位信息)，但不清楚是此群中哪个成员生成的签名.

5) 打开(Open).当出现争议时，GM可打开签名找出真正的签名者.

由上述定义可见，与普通的群签名相比，层次匿名群签名在签名时，位于叶子节点的成员可选择匿名级别，即可选择从根到其自身路径上的任一个单位作为匿名范围，上层单位代表匿名性较高(即把自己隐藏在更大的组中)，而下层单位匿名性较低(即其所在单位成员较少).这样一个层次匿名群签名密码系统就可适应多种不同的需求.

知识签名是对消息m的签名，对拥有某个知识(如离散对数、大整数因子分解等)的非交互式零知识证明，通常表示为

SPK{x:x是某个难题的解}(m).

上式中：m是签名的消息；x是签名方拥有的秘密知识(即签名私钥).

而数学难题是签名方案对应的公钥，如著名的基于离散对数和ROM模型的Schnorr签名方案，公钥为{g，h，p}，私钥为x，满足关系h=gxmodp，其签名就是

SPK{x:h=gxmodp}(m).

构造为

上式中:r为随机数；H为ROM的哈希函数；R=grmodp.

验证方程为

定义2可追踪性安全定义模型.博弈游戏定义敌手为A，挑战者为C，即

1) C作为群管理员GM，生成层次群签名各单位的GPK和GSK，并把GPK发给敌手A；

2) 利用GPK，A可以向GM申请加入群成为群成员，并得到成员私钥MSK；A也可以申请得到对某个消息m的群签名Sm；A还可以要求得到某个群成员的私钥MSK；

3) A输出一个消息和签名对(m，Sm)，如果签名合法，且A未要求查询得到过m的群签名，且签名不能被GM追踪为A已经查询过或攻破过的群成员，则称A赢得胜利.

可追踪性安全指没有多项式时间的敌手A能以高概率赢得上述博弈游戏.

2 层次匿名群签名的构建

2.1 构建方法

1) 设置(Setup).最上层群公钥为1个随机多项式(变量个数对应层次结构高度)，即

axi+byj+czk+dwl+evs+fut+g=0 modN.

而下面每层的单位又有1个公钥多项式，变量个数逐渐减少，每个最小的组公钥是1个有2个变量的随机多项式，即

an-1xin-1+bn-1yjn-1+cn-1=0 modN.

假定树的高度为n，类似地，倒数第2层组织的公钥是1个有3个变量的随机多项式，即

an-2xin-2+bn-2yjn-2+cn-2zkn-2+dn-2=0 modN.

另外，要求生成这些随机多项式时，从根到叶子节点上的路径上所有公钥多项式中同一个变量的指数是互素的(主要是为了增强匿名性，使上、下层单位之间的群签名不可链接).

2) 加入(Join).当某个成员要加入时，从最底层开始，随机选择1个xr，那么，GM利用持有的私钥(即N的因子分解p和q)，可解出对应的yr满足

把(xr，yr)代入上一层方程，GM又可以解出zr，满足

mod依次往上，直到最高层得到用户的全部私钥(xr，yr，zr，wr，vr，ur)，满足

3) 签名(Sign).最高层公钥多项式对应的线性化方程为

aX+bY+cZ+dW+eV+fU+g=0 modN.

上式中：X=xi；Y=yj；Z=zk；W=wl；V=vs；U=utmodN.

签名时，签名者公布其Xm，Ym，Zm，Wm，Vm，Um，这些公开信息要满足上述的线性化方程，即

aXm+bYm+cZm+dWm+eVm+fUm+e=0 modN.

然后，零知识证明其拥有相应的私钥，即知识签名表示为

SPK{x，y，z，w，v，u:Xm=xi，Ym=yj，Zm=zk，Wm=wl，Vm=vs，Um=utmodN}(m).

类似地，签名的叶子节点用户可选择从根到其路径上的任一节点单位的公钥多项式，来生成相应的签名，即层次匿名群签名.

证明SPK{x:Xm=xi}(m)可高效实现如下：对消息m的知识签名为(t，T)，其中，t=xH(m)rmodN，r为随机数，T=rimodN；验证签名就是验证方程ti=XH(m)TmodN是否成立.

4) 验证(Verify).由上述可知，签名就是针对某个公钥多项式的知识签名SPK，所以，验证就是验证SPK是否成立.由于SPK的零知识特性，验证方只能知道公开的信息{Xm，Ym，Zm，Wm，Vm，Um}，但不知道具体是哪个成员签署的.

5) 打开(Open).若后期有争议发生，GM利用成员加入时保存的相关信息，根据{Xm，Ym，Zm，Wm，Vm，Um}可以很容易追踪出是哪个成员所做的群签名.因此，GM可利用GSK=(p，q)计算出Xm对应的成员私钥xm，从而在自己的数据库中查找此私钥是分配给哪个用户的.

2.2 一个简单的例子

以简单的二层组织架构为例(更多的层次只需增加变量的个数即可)，最上层有3个变量的随机公钥多项式为

f1(x，y，z)=x5+245y11+137z7+92=0 mod 323(17×19).

设第2层有2个单位，那么，各自可选1个2个变量的随机多项式作为公钥，如

f21(x，y)=x7+135y7+31=0 mod 323，

f22(x，y)=x11+231y5+27=0 mod 323.

对于组织1，GM可根据以下步骤生成成员私钥：随机取x=3，由f21解出y=202，再把(x=3，y=202)代入f1，解出z=39，容易验证

f1(3，202，39)=35+245×20211+137×397+92=0 mod 323，

f21(3，202)=37+135×2027+31=0 mod 323，

即此成员的私钥为MSK=(3，202，39).GM可将此MSK发给成员，并在自己的数据库中保存此MSK和对应成员的身份信息，用于以后打开签名.利用此MSK，成员可以生成群签名.签名时，若此成员想实现最大匿名性，那么，可以利用MSK=(3，202，39)和最高层的公钥多项式

f1(x，y，z)=x5+245y11+137z7+92=0 mod 323，

按以下方式进行签名.先计算

Xm=35mod 323=243，Ym=20211mod 323=179，Zm=397mod 323=248，

并把(Xm，Ym，Zm)作为签名的一部分；然后，针对要签名的消息m，再生成知识签名，即

SPK{(x，y，z):Xm=x5，Ym=y11，Zm=z7}(m).

最终的群签名为

(Xm，Ym，Zm，SPK).

验证签名时，验证方要先验证(Xm，Ym，Zm)是否满足线性化的公钥多项式方程，即Xm+245Ym+137Zm+92=0 mod 323是否成立，这里显然

243+245×179+137×248+92=78 166=242×323=0 mod 323

成立.如果不成立，则拒绝签名；如果成立，再继续验证上述知识签名是否合法.

若此成员想生成一个以其所在的组织1为匿名范围的群签名，那么，可以利用MSK中的(3，202)，先计算

Xm=37=249 mod 323，Ym=2027=297 mod 323.

然后，生成知识签名

SPK{(x，y):Xm=x7，Ym=y7}(m).

验证时，验证方要先验证(Xm，Ym)是否满足线性化的f21，即Xm+135Ym+31=0 mod 323是否成立，这里显然

249+135×297+31=40 375=125×323=0 mod 323

成立.若成立，再验证知识签名是否合法.

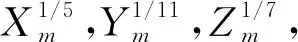
3 安全性分析与证明

定理1基于RSA假设，上述层次匿名群签名时是可追踪的.

证明：挑战者C作为GM生成GPK(即一随机多项式和RSA模数N，变量个数等于组织层次架构高度)，GSK满足N=pq，并将GPK发给敌手A进行如下游戏.

1) A可以申请加入群，此时，C只要利用自己的群私钥GSK生成成员私钥(即对应于公钥多项式的解)发送给A即可.

2) A要求获得对某个消息相对某个群组的群签名，此时，C可以利用自己的群私钥GSK生成相应群组中某个成员私钥；然后，利用此私钥生成相应的层次群签名(即上述知识签名)即可.

3) A要求获得某个群成员的私钥，此时，C利用保存在数据库中该成员的相关信息查找或生成其私钥；然后，发送给A即可.

4) 最后，如果A能够生成1个合法的群签名，而GM不能追踪到该签名的签名方(即A没有查询过此消息此单位的群签名，且A没有从C获得过本次签名中所用的成员私钥)，则称A赢得此次游戏.如果A能以不可忽略的概率赢得游戏，那么，证明利用A可以攻破RSA假设，即A能够造出成员私钥(x′，y′)，满足群公钥多项式

ax′i+by′j+c=0 modN.

首先，找到(X′，Y′)，满足

aX′+bY′+c=0 modN

是简单的，随机选择1个X′，可解此线性方程得到相应的Y′.下面证明要同时获取x′，y′满足

x′i=X′，y′j=Y′ modN

是困难的，即

1) 敌手A可先选择随机的x′，再计算X′=x′i，那么，根据RSA是随机置换的假设，X′是随机的，相应的Y′也是随机的，所以，要对随机的Y′取其j次根，即Y′1/j根据RSA假设是困难的；

2) 敌手A也可以选择已有的X(即从上述游戏中获取的X)，那么，Y也就确定了，此时，GM就可追踪到了.

匿名性：由上述构建可见，群签名就是{Xm，Ym，Zm，…}和SPK，这些显然都不包含任何成员信息，即验证方只能验证签名是否合法，但不知道是哪个成员做的签名，即签名是匿名的.在上述的签名方案中，由于在签名时要公布Xm，Ym，Zm等信息，所以，不是完全匿名的，即同一成员相对同一单位所做的群签名是可链接的，不是完全匿名的.但由于要求在根到叶子节点的路径上，所有公钥多项式中的同一个变量的指数是互素的，则根据RSA是随机置换的假设，公开信息也是随机的，从而在不同匿名级别的签名中，同一个成员是不可链接的.

因此，一个重要的公开问题就是如何构建完全匿名(即同一成员针对同一单位所做的群签名也是不可链接的)的层次匿名群签名方案.

4 讨论

提出一种新的层次匿名群签名的概念，将组织的不同部门单位作为层次机构，叶子节点作为群成员个人，群成员在生成群签名时，可以选择自己的匿名层次，即在签名时可以选择把自己隐藏在小组或大组之中，方便成员在不同的应用中使用不同的签名方式.基于多变量多项式、RSA假设和知识签名技术，构建一个具体的方案，但方案的缺陷在于没有实现完全匿名，只是有限匿名，即同一个成员对同一个单位所做的群签名虽然是匿名的，但是是可链接的.

因此，下一步重要的研究课题就是如何构建实用、高效的完全匿名的层次匿名群签名方案.另一工作方向是降低中心管理员负担，即考虑结合HIBE和文中的层次匿名方案，构建既能实现层次匿名，又能实现层次管理的方案，即上层管理员可以把成员加入等工作委托给下层单位管理员，从而缓解中心管理员的负担，并考虑如何做到在中心管理员和下层管理员之间合理的工作分配问题，综合考虑管理员的成员密钥生成工作、成员撤销工作及签名打开等工作的合理分配与协调.