高轴压比柱脚拉杆约束方钢管超高强混凝土柱抗震性能试验

季相濡， 胡红松，2， 许力

(1. 华侨大学 土木工程学院， 福建 厦门 361021；2. 华侨大学 福建省结构工程与防灾重点实验室， 福建 厦门 361021；3. 福建工程学院 土木工程学院， 福建 福州 350100)

方钢管混凝土(SCFST)柱因强度高、延性好、施工便捷等优点，已被广泛地应用于超高层建筑工程实践中[1].在SCFST柱中内填超高强混凝土可有效提高轴向承载力.然而，超高强混凝土脆性特征显著，当承受高轴压比时，方钢管超高强混凝土(SUCFST)柱的变形能力不足[2].对SCFST柱进行二次约束可有效提高变形能力.在各种约束构造中，约束拉杆不仅可以约束内填混凝土，还可以在约束外包钢管局部屈曲的发生和发展方面起到良好的作用[3]，而钢管的局部屈曲发展是导致钢管混凝土(CFST)柱承载力退化的重要因素之一[4].此外，在强地震作用下，框架柱的损伤通常集中于柱脚塑性铰处.

目前，大多是对沿柱高通长布置约束拉杆的SCFST柱进行研究.Hsu等[5]以轴压比、钢管宽厚比、约束拉杆直径为参数，对12根柱脚拉杆约束SCFST柱和6根无拉杆约束对比试验柱进行水平往复加载试验，结果表明，柱脚拉杆约束可显著增强组合柱的变形能力，增加柱脚拉杆的数量可有效增强SCFST柱的抗震能力.Cai等[6]对10根带约束拉杆的SCFST柱和5根无约束拉杆的对比柱进行轴压试验研究，结果表明，约束拉杆可有效提高SCFST柱在轴向荷载下的极限强度和延性，增大配置拉杆的直径可显著提高组合柱的极限承载力，使承载力退化更加缓慢.王英涛等[7]对2根无约束拉杆的SCFST柱和8根带约束拉杆的SCFST柱进行拟静力试验，验证约束拉杆对提高SCFST柱的极限强度、变形能力具有有效性.目前，对带约束拉杆的SCFST柱抗震性能方面的研究较少，且内填混凝土抗压强度均不高于60 MPa.因此，本文对2根无拉杆约束SUCFST柱和2根柱脚拉杆约束SUCFST柱(内填混凝土轴心抗压强度为120 MPa)开展高轴压比下的水平低周往复加载试验，研究高轴压比下柱脚拉杆约束SUCFST柱的抗震性能.

1 试验方案

1.1 试件设计

设计制作2根无拉杆约束SUCFST柱(试件编号为C-0-0.47，C-0-0.42)和2根柱脚拉杆约束SUCFST柱(试件编号为C-2-0.47，C-3-0.42).SUCFST柱(组合柱)外包钢管的宽厚比为31，满足我国行业标准JGJ 138-2016《组合结构设计规范》[8]中宽厚比限值的规定.柱脚拉杆约束SUCFST柱的约束拉杆采用10.9级M10牙条切割制成，使用10.9级法兰螺母从钢管外侧固定约束拉杆两端，并布置于试验柱基础梁顶面240 mm高度范围内的柱体上，同向约束拉杆竖向间距和水平间距相等.柱脚拉杆约束试件的构造，如图1所示. 图1中：柱脚拉杆约束试件的构造去除拉杆，即为无拉杆约束试件的构造.

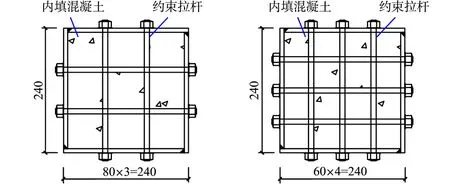
(a) A-A截面 (b) B-B截面

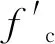
表1 试件参数

1.2 材性实测

1.3 加载装置与量测方案

试验加载装置，如图2所示.反力梁和转换梁通过螺栓连接(固定装置)，用于适配滑板尺寸，并提供轴向反力；滑板、摩擦力测量装置[10]、竖向作动器由上到下依次通过螺栓连接(随动装置)，在持续施加轴力的同时进行水平低周往复加载，可测得滑板与转换梁间的摩擦力.定义作动器的推出方向为正向，缩回方向为负向.

图2 试验加载装置(单位:mm)

首先，采用力控制，施加轴力直至目标值.然后，采用位移控制，匀速(0.1 mm·s-1)施加水平荷载，并且保持轴向荷载不变.水平低周往复加载按照位移角(θ)分别为0.25%，0.50%，1.00%，1.50%，每级循环3轮，位移角分别为2.00%，2.50%，3.00%，每级循环2轮的顺序逐级加载，当水平荷载不足0.5Fm(Fm为水平峰值荷载)时，结束加载.

试验测点的布置，如图3所示.图3中：D1～D5分别为位移计测点.使用位移计测量试件相应位置的水平位移或竖向位移，使用电阻应变片测量各测点的纵向应变数据.试件钢管的腹板和翼缘均布置纵向应变片，其中，无拉杆约束试件的应变片布置与试件C-2-0.47(图3(b)，图3(c))相同.由于约束拉杆的分布不同，试件C-3-0.42的应变片布置与试件C-2-0.47略有不同，但不影响二者之间的比较.

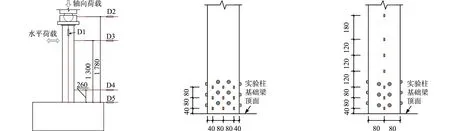
(a) 位移计 (b) 试件C-2-0.47腹板应变片 (c) 试件C-2-0.47翼缘应变片

2 试验结果与分析

2.1 试验现象

当位移角θ=-1.00%，水平荷载F=Fm时，试件C-0-0.42的内填混凝土发生压溃；当θ=1.30%，F=Fm时，试件C-0-0.47的内填混凝土发生压溃.当θ=-1.50%，F=0.86Fm时，试件C-0-0.42出现局部屈曲；当θ=1.40%，F=0.87Fm时，试件C-0-0.47出现局部屈曲.随着加载的进行，这两个试件钢管四面均在距基础梁顶面100 mm高度处陆续出现局部屈曲.当θ=-1.90%，水平荷载F降至0.50Fm以下时，试件C-0-0.42停止加载；当θ=-1.40%，水平荷载F降至0.50Fm以下时，试件C-0-0.47停止加载.相较于试件C-0-0.42，由于试件C-0-0.47的轴压比更高，故局部屈曲出现得更早，变形能力较差.

当θ=2.00%，F=Fm时， 试件C-2-0.47的内填混凝土发生压溃；当θ=2.50%，F=Fm时，试件C-3-0.42的内填混凝土发生压溃.随后，两个试件钢管左侧翼缘板在距离基础梁顶面320 mm处出现局部屈曲，且局部屈曲是位于约束拉杆区域上方， 发生时刻均晚于相应的无拉杆约束试件.

最终，当θ=2.50%，水平荷载F降至0.5Fm以下时，试件C-2-0.47停止加载；而当θ=3.00%，水平荷载F降至0.5Fm以下时，试件C-3-0.42停止加载.这表明柱脚拉杆可有效地延缓局部屈曲的发生，增强组合柱的变形性能.

4个试件内填混凝土压溃位置均位于外包钢管发生屈曲的高度范围内.试件的破坏形态，如图4所示.由图4可知：试件C-0-0.42，C-0-0.47的破坏集中在距离基础梁顶面100 m高度处；试件C-2-0.47，C-3-0.42的约束拉杆区域混凝土相对完好，破坏集中于约束拉杆区域之上，这表明若设置约束拉杆的强度较高，破坏位置会转移至未布置约束拉杆区域中受弯较大的位置.

(a) 试件C-0-0.47 (b) 试件C-0-0.42

2.2 弯矩-位移角滞回曲线

由于无拉杆约束试件发生破坏的临界截面与柱脚拉杆约束试件不一致，故统一选取柱底截面(基础梁顶面)作为评估组合柱截面性能的计算截面.截取球形铰链至临界截面间的部分为组合柱隔离体，其受力分析如图5所示.图5中：f为隔离体顶部所受水平荷载(与转换梁和滑板之间的摩擦力等值)；ht，Δt分别为隔离体顶部到基础梁顶面的距离(1 300 mm)和水平方向位移；hl为水平荷载作用点到基础梁顶面的距离(1 780 mm)；M为弯矩；V为剪力.

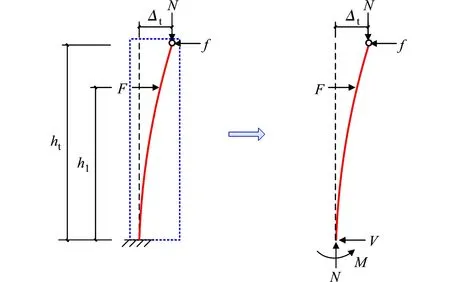
图5 组合柱隔离体的受力分析

临界截面处的弯矩Mb为

Mb=F×hl+N×Δt-f×ht

.

(1)

临界截面弯矩与位移角的关系，如图6所示.由图6可知：当试件受压翼缘钢板初始屈服发生时，位移角均小于0.30%；试件C-0-0.42，C-3-0.42的受压翼缘钢板初始屈服约发生在θ为0.25%时； 试件C-0-0.47，C-2-0.47的受压翼缘钢板初始屈服约发生在θ为0.20%时，表明在更高的轴压比下，外包钢管更易屈服；无拉杆约束试件在θ为1.50%的循环荷载作用下，发生内填混凝土压溃；试件C-2-0.47，C-3-0.42分别在θ为2.00%，2.50%的循环荷载作用下，发生内填混凝土压溃.这表明柱脚拉杆约束可有效地延缓混凝土压溃的发生，钢管局部屈曲均发生在内填混凝土压溃的同级或下一级位移角范围内.

(a) 试件C-0-0.47 (b) 试件C-0-0.42

2.3 受弯承载力与变形性能

试件的骨架曲线，如图7所示.

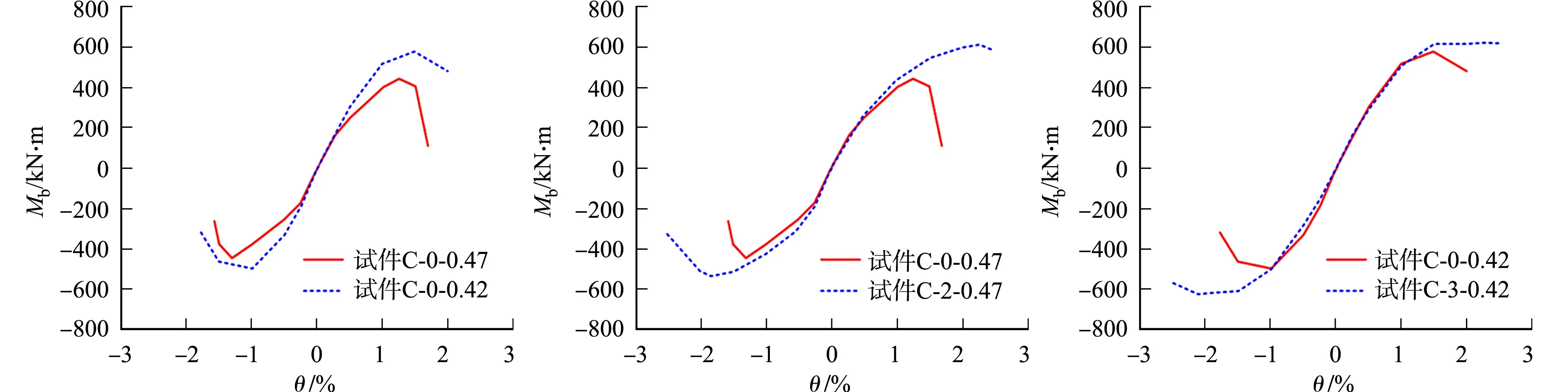
(a) 轴压比的影响 (b) 2列约束拉杆的影响 (c) 3列约束拉杆的影响

受弯承载力和变形性能试验结果，如表2所示.表2中：Mb，m为临界截面峰值弯矩；θy为屈服位移角，是骨架曲线上升段中0.75Mb，m对应位移角的4/3倍[11]；θm为峰值弯矩对应的位移角；θu为极限位移角，是骨架曲线下降段中0.80Mb，m对应的位移角[12]；μ为延性比，μ=θu/θy；括号中的值为加载停止前该加载方向极限位移角和由此得到的组合柱延性比；由于加载停止时临界截面弯矩没有减小到峰值弯矩的80%，故实际的极限位移角和相应的延性比应更大.

由表2可知：除了试件C-0-0.42的负向之外，各试件的屈服位移角θy均在1.00%～1.50%之间，相对稳定； 相较于试件C-0-0.42，C-0-0.47， 因轴压比更高，故受弯承载力、极限位移角(低15%左右)和延性比(低26%左右)更低；相较于相应的同轴压比的无拉杆约束试件，柱脚拉杆约束试件C-2-0.47，C-3-0.42的屈服位移角(高30%左右)、受弯承载力(高15%左右)、极限位移角和延性比均更高，表明配置约束拉杆可有效地提高SUCFST柱高轴压比下的受弯承载力和变形性能.试件C-2-0.47，C-3-0.42的极限位移角均在2.23%～2.50%之间，满足文献[13]规定的框架柱弹塑性层间位移角限值.

表2 受弯承载力和变形性能的试验结果

2.4 承载力退化

由于试件内填混凝土损伤和钢管塑性变形累积，组合柱在相同级别位移角下，受弯承载力随循环次数的增大而降低.引入承载力退化系数ηj，有

ηj=M2，j/M1，j.

(2)

式(2)中:Mi，j为试件临界截面在第j级往复加载位移角下，第i个循环中相应加载方向的最大弯矩[13].

试件的承载力退化曲线，如图8所示.由图8和表2可知：承载力退化系数总体与位移角绝对值呈负相关；当θ<θm时，各试件承载力的退化系数均十分接近1，表明所有试件几乎未发生受弯承载力退化；而当θ≥θm后，承载力的退化现象较为明显；由于柱脚设置约束拉杆，试件C-2-0.47的承载力退化系数整体大于试件C-0-0.47，当加载到较大位移角时更为明显；试件C-3-0.42，C-0-0.42也反映出相同的规律.由此可知，配置约束拉杆有利于减轻SUCFST柱的承载力退化.

图8 试件的承载力退化曲线

2.5 耗能性能

低周往复加载滞回环围合面积可反映试件在该循环的耗能量[14].试件的耗能曲线，如图9所示.图9中：E为试件在各级水平低周往复加载下的单圈耗能量；Ea为水平低周往复加载下的累计耗能量.

(a) 单圈耗能量 (b) 累计耗能量

由图9和表2可知：试件的单圈耗能量与位移角呈正相关；当θ<θm时，各试件在同级位移角下的单圈耗能量差异较小；而在相同轴压比下，柱脚增设拉杆对单圈耗能量并无明显的影响.但相较于试件C-0-0.47，C-2-0.47的累计耗能量提高了156%；而相较于试件C-0-0.42，C-3-0.42的累计耗能量提高了228%， 因此配置约束拉杆可有效地提高SUCFST柱的耗能性能； 当θ>θy时，相较试件C-2-0.47，约束拉杆间距更小的试件C-3-0.42具有更强的单圈耗能量，故减小拉杆间距有利于增强SUCFST柱的耗能性能.

3 结论

在高轴压比下，对2根无拉杆约束SUCFST柱和2根柱脚拉杆约束SUCFST柱进行水平低周往复加载试验，可得以下4个结论.

1) 增设约束拉杆能够显著提高SUCFST柱的受弯承载力、变形性能和耗能性能.

2) 减小约束拉杆间距有利于提高大位移角下(θ>1.50%)SUCFST柱的单圈耗能量.

3) 增大轴压比对SUCFST柱的变形性能存在不利影响.当轴压比从0.42增加至0.47时，SUCFST柱的极限位移角约减小15%，延性比约降低26%.

4) 若设置拉杆的约束效应太大，SUCFST柱的破坏位置会转移至约束拉杆区域上方，需进一步研究合适的柱脚拉杆配置率.