拦截大机动目标的有限时间收敛制导律*
2022-11-12吴刚张科
吴刚 ,张科
(1. 西北工业大学 航天学院,陕西 西安 710072;2. 江南机电设计研究所,贵州 贵阳 550009)
0 引言
随着航空航天技术的进步,特别是以高超声速飞行器为代表的现代空袭武器机动能力越来越强,而且它的飞行轨迹难以预测[1],这给拦截他们的导弹带来了新的挑战。为了增强对目标的毁伤效果,不仅仅需要导弹拦截目标时,脱靶量尽可能地小[2],而且还需要导弹以特定的角度拦截目标[3]。因此研究考虑攻击角约束拦截大机动目标的制导律具有重要的意义。
目前,比例制导律因其实现简单,在工程上得到了广泛应用[4-7],而传统的比例制导律,不能实现让导弹以期望的角度攻击目标。为此,学者们对传统的比例制导律进行了改进[8],让其实现以期望的角度拦截目标。然而,比例制导律及其改进形式仍然针对的是非机动目标。它们拦截机动目标的效果并不理想。
为了实现对机动目标的拦截,学者们将许多先进的现代控制理论成果应用到制导律的研究。如基于最优控制理论的最优制导律[9],基于自适应控制理论的自适应制导律[10],基于微分对策理论的微分对策制导律[11]等。
相对于其他制导方法,滑模制导律结构简单,设计方便,易于工程实现,而且对目标机动等引起的制导系统扰动具有较强的鲁棒性,被广泛地应用于拦截机动目标的制导律设计[12]。传统的滑模控制只能实现无限时间的渐进收敛,而导弹拦截目标时,末制导时间很短,因此,设计制导律时考虑有限时间收敛更有工程实际应用价值。
在滑模制导律设计过程中,制导系统扰动通常通过选择合适的开关增益来消除。为了保证制导系统稳定,开关增益的选择通常要大于扰动的上界。这就要求制导系统扰动的上界是已知的,而在工程实际中,制导系统扰动的上界不可能事先知道。为了解决这一问题,文献[13]用自适应律估计制导系统扰动的上界。而仅仅通过开关增益实现滑模制导律对制导系统扰动的鲁棒性,会给制导系统带来严重的抖振现象。
为了消除滑模控制带来的抖振,滑模控制经常与扰动观测器一起使用设计制导律,常用的非线性扰动观测器[14]、扩张状态观测器[15]、高增益观测器[16]等扰动观测器的参数设计,对其估计性能和收敛性能都有较大的影响。参数设计不合理直接影响到导弹的拦截精度。为此,本文提出了参数适应调节的径向基函数(radial basis function,RBF)神经网络扰动观测器,用来估计制导系统扰动。
综上讨论,本文基于有限时间收敛的积分滑模控制理论和参数自适应调节的RBF 神经网络扰动观测器,设计了考虑攻击角约束的拦截大机动目标的有限时间收敛制导律。扰动观测器和连续趋近律的应用避免了滑模制导律的抖振现象。
1 制导模型建立
在二维平面中导弹拦截目标相对运动关系如图 1 所示,图中,M 代表导弹的质心,T 代表目标的质心,可得二维平面内导弹和目标的相对运动的动力学方程为
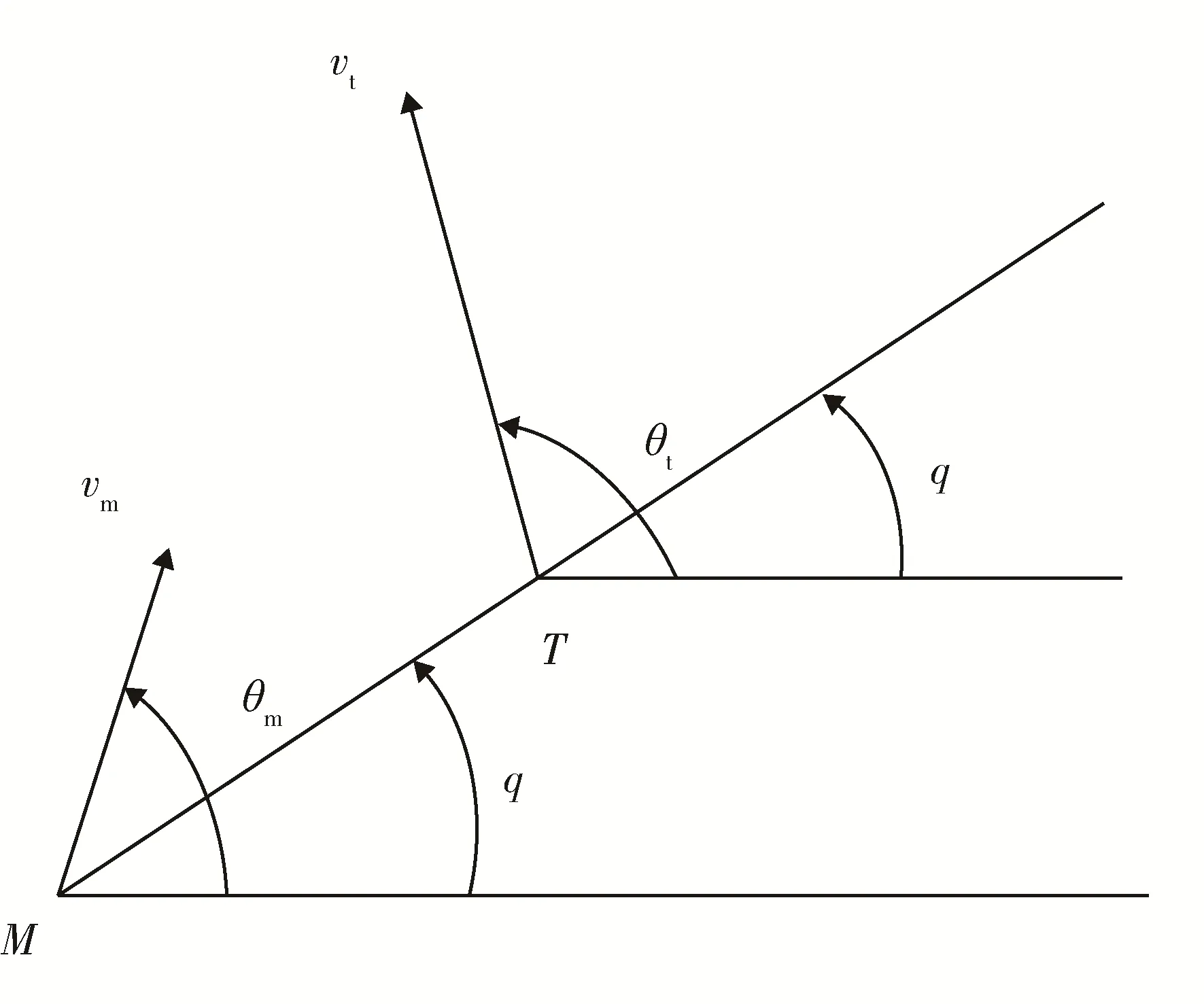
图1 导弹与目标的相对运动几何Fig.1 Relative motion geometry of missile and target
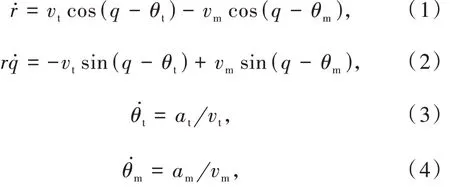
式中:r 为导弹和目标的相对距离;q 为视线角;vm为导弹的速度;vt为目标的速度;θm为导弹速度的方向角;θt为目标速度的方向角;am为导弹的法向加速度;at为目标的法向加速度。
对式(2)求导,得
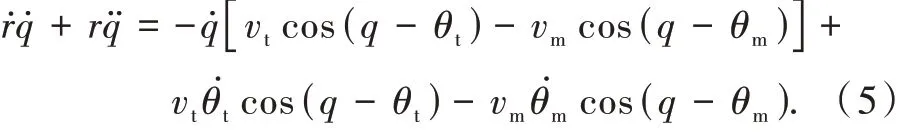
结合式(1)、(3)、(4),式(5)可整理为
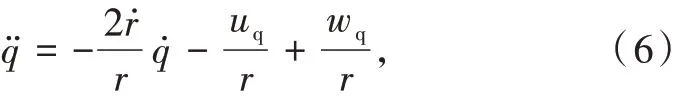
式中:uq= amcos(q - θm)为导弹加速度在弹目视线法向上的分量;wq= atcos(q - θt)为目标加速度在弹目视线法向上的分量。
令 x1= q - qd,x2= q̇,其 中 qd为 期 望 的 终 端 视线角,考虑攻击角约束的二维平面制导方程为
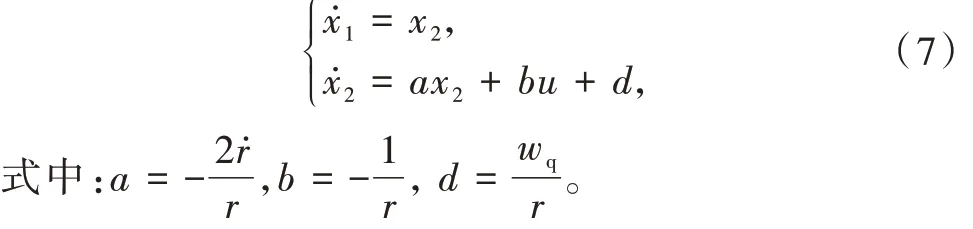
2 制导律设计
2.1 积分滑模制导律设计
在制导律设计之前,为了制导律设计及其有限时间收敛性证明方便,先介绍以下引理:
引理 1[17]如果存在李雅普诺夫函数 V(x)的一阶导数满足不等式

式 中 :a > 0,0 < α < 1,则 系 统 有 限 时 间 收 敛 到原点。
引理 2[18]对于如下 n 阶积分系统
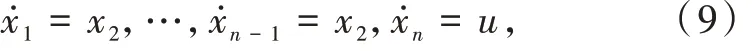
存在 ε ∈ (0,1),对于任意 αn∈ (1 - ε,1),假如设计的控制器为

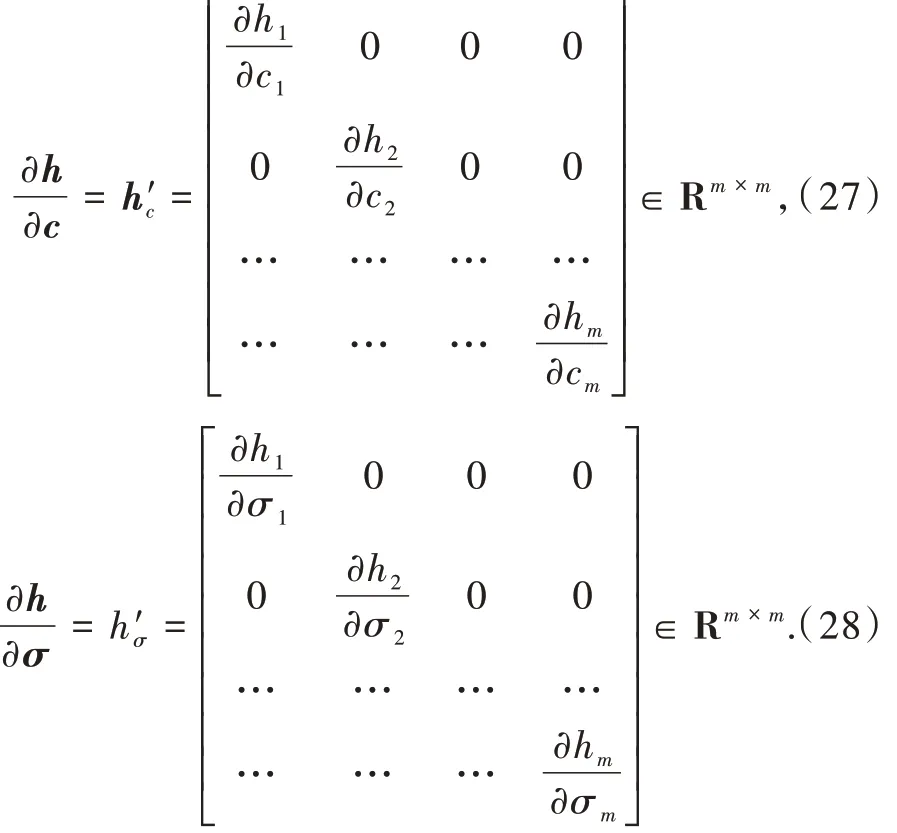
针对制导系统式(7),让导弹以期望的攻击角精确拦截大机动目标,为了使系统状态有限时间收敛,设计如下积分滑模面:
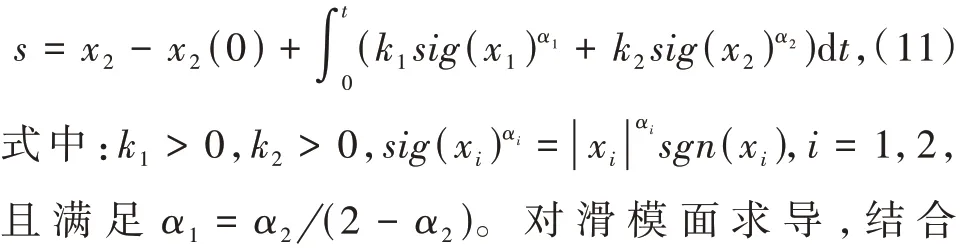
式(7)得
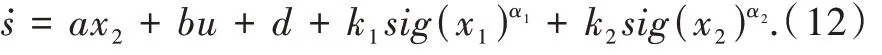
为了使系统状态轨迹从初始状态快速收敛到设计的滑模面,设计一种快速变幂次趋近律如下:
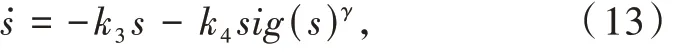
式中:k3> 0,k4> 0,0 < γ < 1。
设计制导律如下:
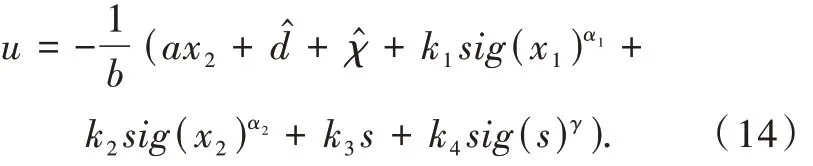
这里d̂为制导系统扰动d 的估计,下文中用神经网络扰动观测器对扰动d 进行估计。χ̂为自适应项,将在下文中定义。
定理1 针对制导系统(7),选择滑模面如式(11),趋近律如式(13),导引律如式(14),则制导系统状态在有限时间收敛到0 附近。
证:选取李雅普诺夫函数V1为

假设制导系统扰动的剩余估计误差为
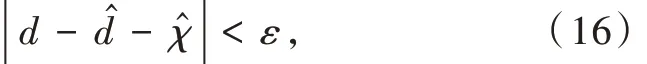
式中:ε 为一个较小的正数。
对V1求导并整理得
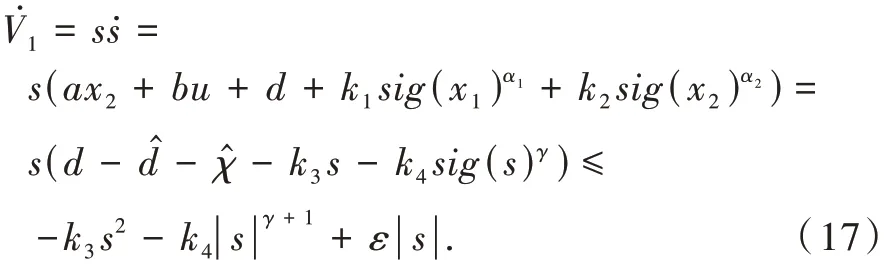
将式(17)写作如下形式

当 k3|s| - ε ≥ 0 时,即|s| ≥ ε/k3时
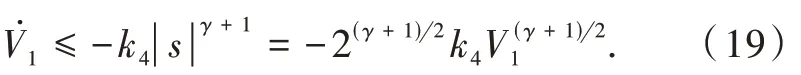
由引理1 和不等式(19)可知,滑动流形s 在有限时间内收敛到一个小的区域|s| ≤ ε/k4= ε1,ε1是一个很小的正数。
s 收敛后,令 s = μ,| μ | < ε1,此时可得

s 收敛后,ṡ= μ̇= 0,因此对式(20)求导得
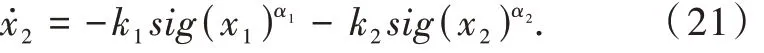
根据引理 2,x1、x2有限时间收敛到 0,也就是说,制导系统在有限时间内,视线角q 收敛到期望的视线角qd,视线角速率q̇收敛到0。定理1 得证。
本文相对于传统的滑模控制所做的改进如表1所示,采用积分滑模面,可以让滑模面有限时间收敛,而传统的线性滑模面只能实现无限时间的渐进收敛,在趋近律设计中在传统的幂次趋近律的基础上增加了指数趋近项,加快滑模面的收敛速度。

表1 本文滑模相对于传统滑模所做的改进Table 1 Improvement of sliding mode compared with traditional sliding mode in this paper
2.2 RBF 神经网络扰动观测器设计
为了实现对大机动目标的精确拦截,对目标机动d 引起的制导系统扰动进行精确的估计是十分必要的,为此,本文提出了一种参数自适应调节的RBF 神经网络对其进行精确估计,扰动d 的表达式为

式中:Ŵ = (ŵ1,ŵ2,…,ŵm)T为 RBF 神经网络输出层的自适应调整的输出权向量;ĥ= (ĥ1,ĥ2,…,ĥm)T为RBF 神经网络隐层神经元的高斯激活函数向量,其参数可以自适应调整,ĥj的元素表示为
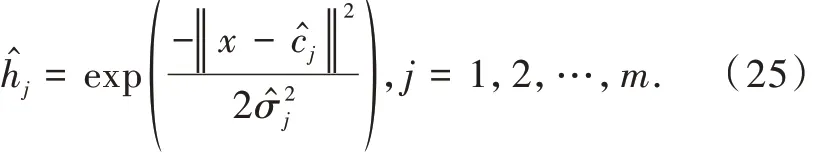
扰动d 和扰动的估计d̂做差,并利用线性化方法展开为泰勒展开式部分线性形式,得到
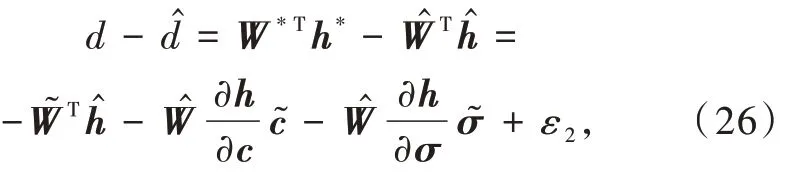
式 中 :W͂ = Ŵ - W*为 RBF 神 经 网 络 线 性 输 出 层 自适应权向量Ŵ与最优权向量W*之间的权向量偏差;c͂= ĉ- c*为高斯函数自适应中心向量 ĉ与最优中心向量 c*之间的偏差中心向量;σ͂ = σ̂ - σ*为宽度向量在自适应宽度向量σ̂与最优宽度向量σ*之
将式(14)代入式(12)整理得
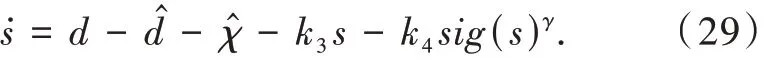
将式(26)代入式(29)得
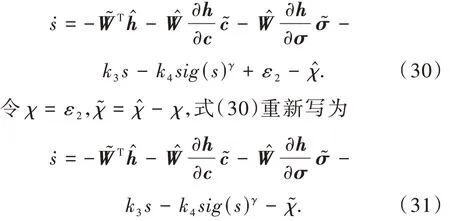
选取李雅普诺夫函数为
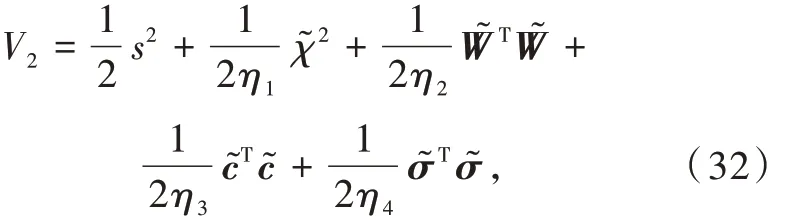
式中:η1,η2,η3,η4为要设计的参数。
对李雅普诺夫函数求导得
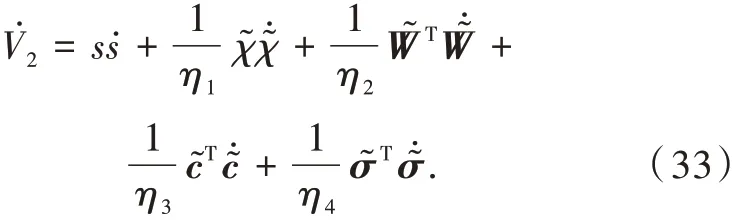
将式(31)代入式(33)得
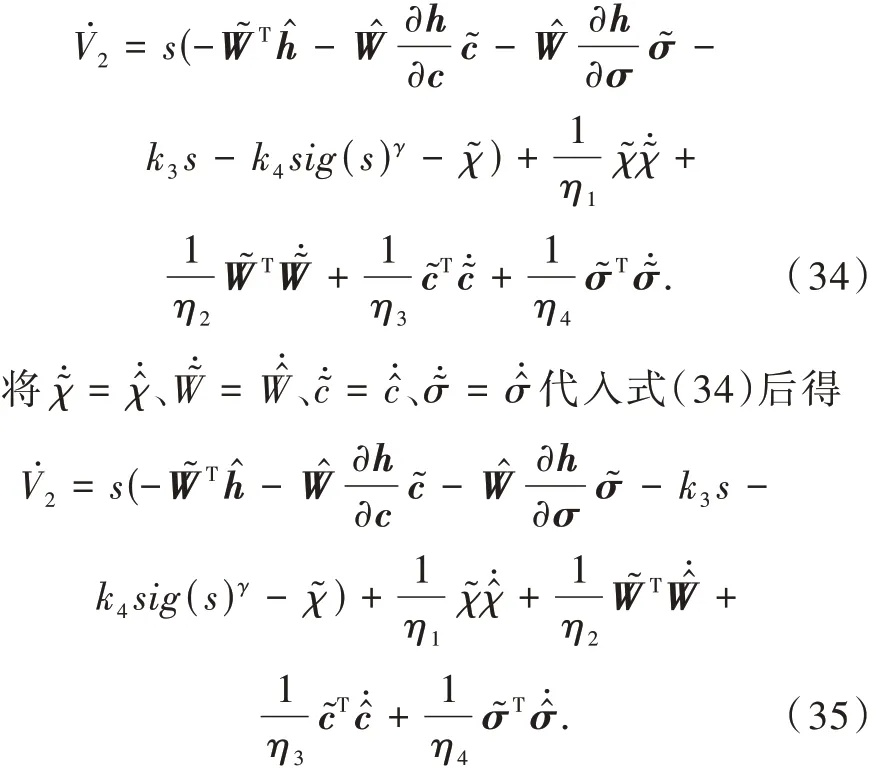
重新整理式(35)得
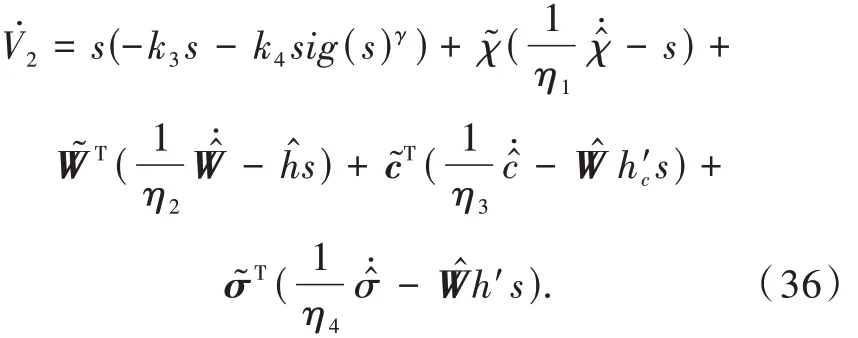
为了保证李雅普诺夫函数的一阶导数V̇0<0,选取随时间变化的自适应参数为
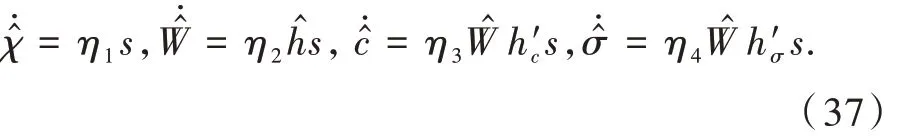
3 仿真校验
为了说明本文所提制导律对大机动目标优异的制导性能,在相同仿真条件下将其与比例制导律(PNGL)和非线性终端滑模制导律(NTSMGL)[19]进行对比仿真。仿真中,选取3 组不同的导弹和目标的初值如表2 所示。

表2 3 组不同的导弹和目标仿真初值Table 2 Initial condition of the missile and the target for the simulation
目标机动的加速度设置为拦截难度较大的正弦跳跃式机动,at= 200sin(0.5t)m/s2。通过大量的仿真将比例制导律(PNGL)的比例系数调整到拦截效果最好,非线性终端滑模制导律(NTSMGL)的制导参数按照文献[19]选择。本文所提积分滑模制导律(ISMGL)的参数选择如下:
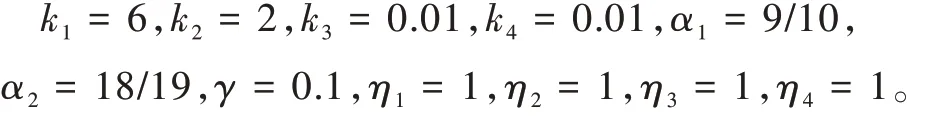
制导律中积分变量参数的初始值选取如下:
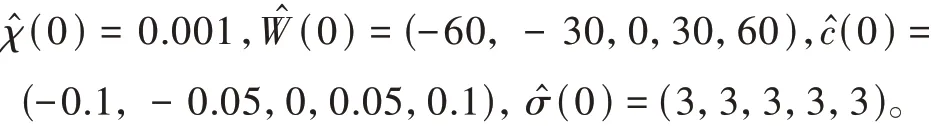
拦截目标时,设置期望的终端视线角qd= 15°。
针对3 组不同的导弹和目标初始值条件,3 种不同制导律拦截正弦跳跃式机动目标的仿真结果如表 3 和图 2~4 所示。从图 2a)、3a)、4a)中可以看出,在3 种不同的制导律作用下的导弹虽然运动轨迹不同,但都能成功的拦截目标。从图 2b)、3b)、4b)中可以看出,在本文所提的积分滑模制导律(ISMGL)和非线性终端滑模制导律(NTSMGL)作用下的导弹视线角都能收敛到期望的值附近,积分滑模制导律(ISMGL)视线角的收敛精度明显高于非线性终端滑模制导律(NTSMGL),而比例制导律(PNGL)视线角不能收敛到期望的值。从图2c)、3c)、4c)中可以看出,本文所提的积分滑模制导律(ISMGL)可以保证弹目视线角速率收敛到零附近,非线性终端滑模制导律(NTSMGL)虽然也可以让弹目视线角速率收敛到零附近,但是在弹目遭遇前的一小段时间会发散,收敛精度和收敛速度也远不如本文所提的积分滑模制导律(ISMGL)。图 2~4(d)为制导指令曲线,本文所提的积分滑模制导律(ISMGL)和比例制导律(PNGL)制导指令曲线比较平滑,而非线性终端滑模制导律(NTSMGL)制导指令曲线出现了震荡现象。表3 为3 种不同制导律的仿真结果统计,在飞行时间方面它们差别不大,在脱靶量和视线角控制方面本文所提的制导律明显优于其他2 种制导律。这充分说明本文所提的制导律具有优异的制导性能。
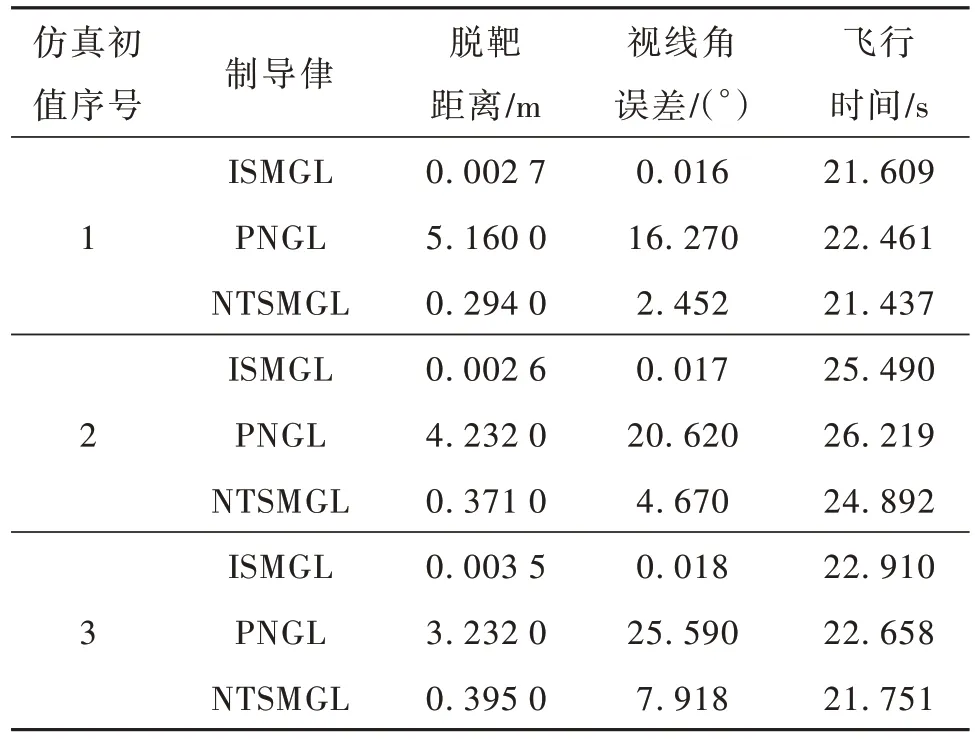
表3 3 种不同制导律的仿真结果Table 3 Simulation results of three different guidance laws
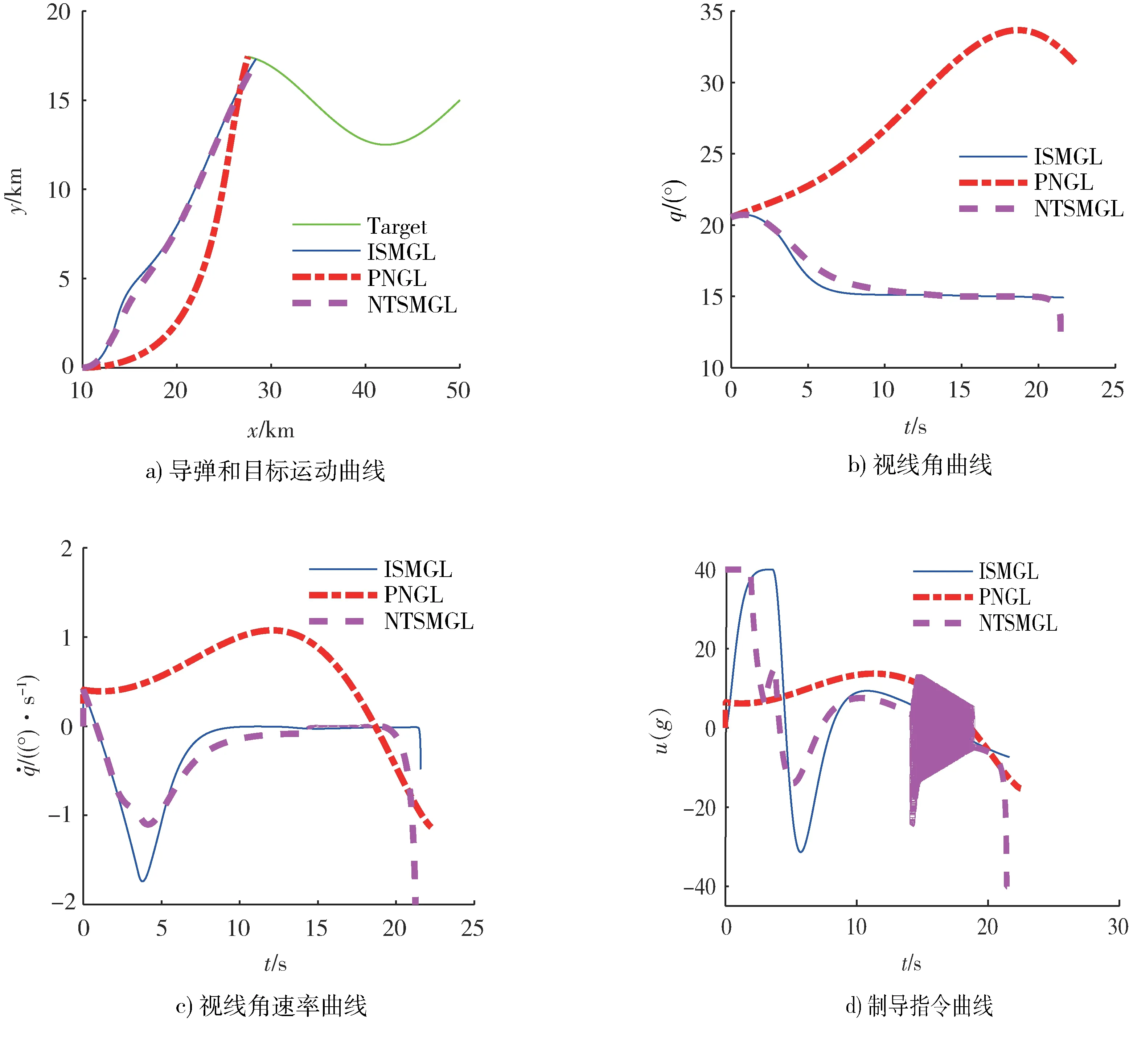
图2 初值1 下不同制导律仿真对比曲线图Fig.2 Simulation comparison curves of different guidance laws under initial value 1
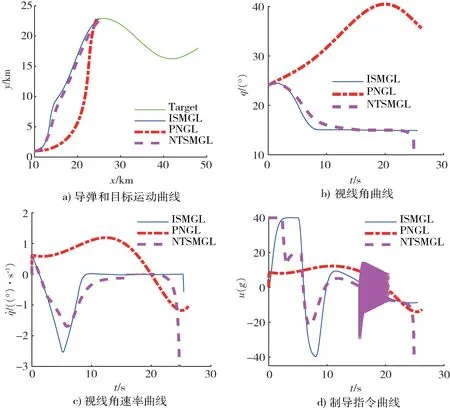
图3 初值2 下不同制导律仿真对比曲线图Fig.3 Simulation comparison curves of different guidance laws under initial value 2
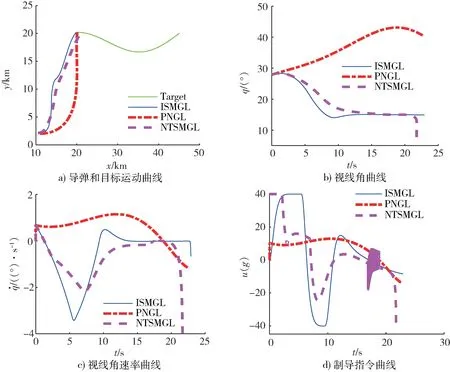
图4 初值3 下不同制导律仿真对比曲线图Fig.4 Simulation comparison curves of different guidance laws under initial value 3
4 结束语
本文以拦截大机动目标为背景,采用积分滑模控制和RBF 神经网络扰动观测器,设计了弹目视线角和视线角速率有限时间收敛的积分滑模制导律。利用李雅普诺夫理论分析了所设计制导律的稳定性。在相同的条件下,通过将其与非线性终端滑模制导律(NTSMGL)和比例制导律(PNGL)对比仿真,说明本文所提积分滑模制导律具有优异的制导性能。可以为拦截大机动目标制导律的设计提供一定的理论和实际参考。
