体育数据分析中一元线性回归的三种方法

胡海涛 喻 孜

体育数据分析中一元线性回归的三种方法

胡海涛 喻 孜

（南京林业大学 体育教育部 理学院，江苏 南京 210037）

一元线性回归是体育数据分析中常用的一种数据处理方法。很多数据处理软件内置的一元线性回归功能都是基于最小化方差(LS)的最小二乘法回归。文章探讨最小化点到直线距离（LD）的回归和Theil-Sen（TS）回归，作为国内现有体育数据分析方法的补充。LS方法数学形式更为简洁，LD方法与作图法采用的策略相同，TS方法计算量较大。以安踏体育在国内市场占有率数据和高校学生体育课成绩数据为例，比较了三种线性回归算法的异同。在数据具有明显的线性特征时，三种回归算法效果接近。当数据有少数“离群值”时，使用TS回归效果更好。当数据有“类椭圆”分布特征时，LD方法最优。

线性回归；最小二乘法；Theil-Sen回归

回归分析是利用数理统计方法建立因变量与自变量之间的函数表达式。回归分析中,当研究的因果关系只涉及因变量和一个自变量，并且两者的关系为线性时,叫做一元线性回归分析。一元线性回归在体育数据分析中有广泛的应用[1-4]。很多体育数据，往往是一个时间序列，具有趋势性、周期性和随机性。在分析这类数据时，一元线性回归分析能够快速判断出因变量随自变量的变化趋势，从而为数据预测提供帮助。目前，体育统计学中经常采用SPSS统计和EXCEL软件进行回归分析[3-6],这些软件所采用的一元线性回归都是基于最小化方差的回归。很多体育数据分析的文献所讨论的最小二乘法回归，也都是基于最小化方差的回归[7-8]。事实上，一元线性回归还有其他的方法，当数据呈现不同特征时，不同的方法会有不同的效果。目前在体育数据分析领域中，对其他一元线性回归方法的讨论还比较少。文章将讨论三种一元线性回归方法，并对三种方法在物理实验中的应用效果进行比较。

1 一元线性回归的三种算法

1.1 最小化方差的一元线性回归（LS）

上式中，i代表自变量和因变量的第i组数据。对目标函数而言，方差(a,b)应该取极小值。这样，总的看起来，目标函数与所有数据点的“贴合度”最高。后文将这种最小化方差（Least squaring）的回归法简称为LS线性回归。函数(a,b)极小值条件为，

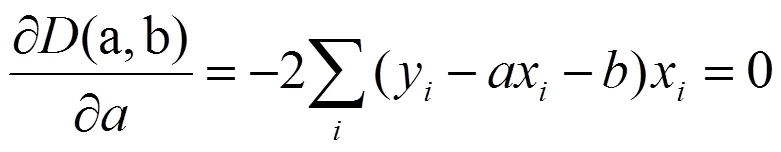
假设共有n组数据，（2）和（3）联立求解即可得到a和b,

1.2 最小化距离的一元线性回归（LD）

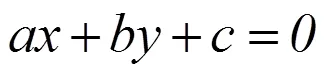
（8）式与（9）比较，消去a和b，可以得到

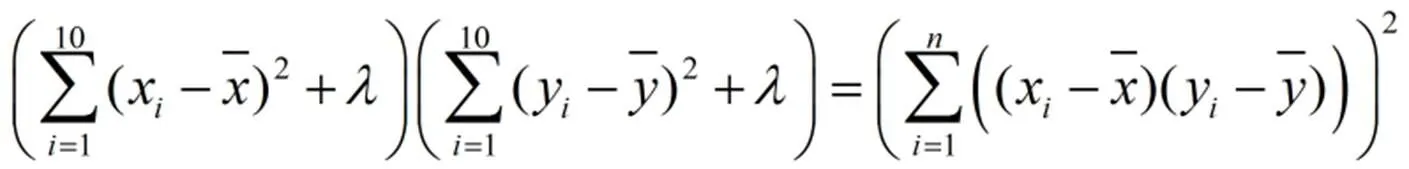
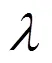
1.3 Theil-Sen一元线性回归（TS）

前述两种方法都是通过极值方程的求解得到直线方程的参数，Theil-Sen一元线性回归（后文简称为TS回归）则是通过中值估计来得到方程参数。假设目标直线斜率为a截距为b。TS回归中a的值等于所有数据点之间斜率的中位数，然后用同样的方法确定b。

2 不同回归方法的比较

三种回归算法中，LS方法的数学形式最为简洁清晰，并且可以直接得到方差估计，因而被广泛用于数据处理。LD方法数学推导最为复杂，然而LD方法采用的策略与作图法一致，因此更容易理解。TS回归法需要比较所有数据点之间的斜率，计算量较大。当测量数据具有不同特征时，三种回归方法有不同的效果。本文通过三组数据来比较三种回归算法之间的区别。

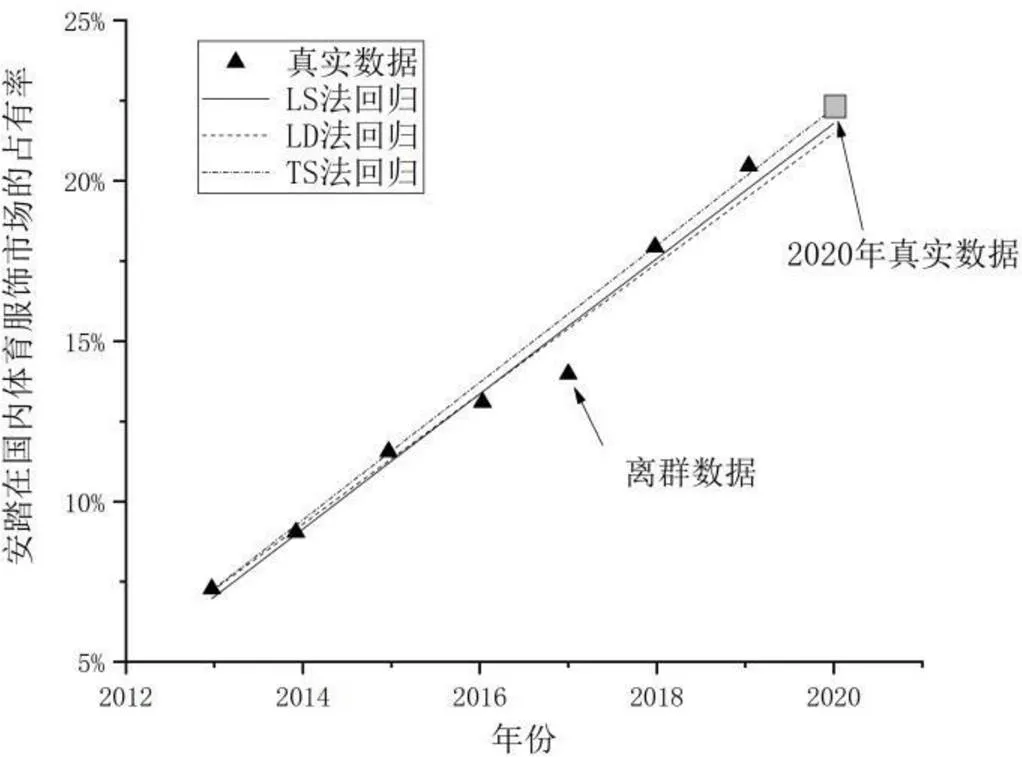
图1 安踏体育在国内体育用品市场的市场占有率随时间的变化

图1为2012年到2019年间安踏体育在国内体育用品市场的占有率。增长趋势具有明显的线性特征。如果增长趋势在短期内可以延续，则可以通过一元线性回归法分析2012-2019年的数据增长趋势，预测2020年的营收数据。用三种回归方法对2012-2019年的数据进行处理，结果如图1的回归线所示。从图1可以看到， TS法和LD法得到的直线几乎重合，LS方法得到的直线斜率较另外两种方法得到的直线斜率稍大。LS法、LD法和TS法预测得到的2020年的结果分别为，15.2%，15.1%和15.0%。图1中方块点代表了2020年的真实数据，值为15.4%。三种方法的预测效果都比较准确，差别不大。

图中三角形代表2012年-2019年的数据，方块代表2020年的数据。基于2012年-2019年的数据采用三种不同的方法做回归分析来预测2020年的数据。

图2 安踏体育在国内体育服饰市场的市场占有率随时间的变化

图中三角形代表2012年-2019年的数据，方块代表2020年的数据。基于2012年-2019年的数据采用三种不同的方法做回归分析来预测2020年的数据。

图2为2012年到2019年间安踏体育在国内体育服饰市场的占有率。与图1类似，增长趋势具有线性特征。用三种方法对2012-2019年数据进行回归处理，预测2020年的市场占有率，结果如图2的回归线所示。可以看到，LS方法和LD方法较为接近，此时TS方法得到的结果与这两种方法明显不同。LS法、LD法和TS法预测得到的2020年的结果分别为，21.7%，21.5%和22.7%。

图1中方块点代表了2020年的真实数据，值为22.7%。与2020年的真实数据相比，TS方法明显更为准确。这是因为2017年的数据（如图箭头所标识的数据）较其他年份数据有较大差距，LS方法和LD方法受到了“离群”数据的干扰，回归直线会偏向这个离群数据。而TS方法是通过中值估计来得到直线，抗干扰能力更强。

在高校体育课中，有部分学生会既选修足球课也参加八百米跑测试。图3为某高校本科生足球课综合成绩和800m测试成绩的分布图。 从数据分布来看，总体趋势是学生800m成绩越高，足球成绩也越高。然而，由于调查样本较多，数据比较离散，分布呈现了“类椭圆”特征。可以通过回归直线法分析两项成绩的关联趋势。用三种回归方法得到回归线如图3所示。此时，TS方法和LS方法结果相近，与LD方法出现明显差异。LD方法使得各点到目标直线垂直距离最小，该方法得到的目标直线更接近于“类椭圆”的主轴，体现了总的统计平均效果，结果更优。

图3 某高校本科生800m成绩和足球课成绩分布

3 结论

体育数据分析中可以用到三种回归算法。LS和LD方法都是采用数学极值法求解最佳直线。LS方法数学形式较为简洁，LD方法推导过程较为复杂。从几何意义上来看，LD方法与作图法采用的策略相同。LS和LD方法都会受到少数“离群数据”的干扰，而TS回归法抗干扰能力更强。当数据存在“离群”数据时，可以考虑使用TS方法回归。但是TS方法的计算量较大，因此，在数据呈现明显线性特征并且没有“离群数据”时，可以选择LS方法或者LD方法。另一方面，数据存在类椭圆分布特征时，用LD方法效果更好。

现在很多数据处理软件，包括origin、spss和Excel都含有直线拟合功能。很多研究[3-8]都对这两种软件在体育数据分析中的应用进行了讨论，并建议使用这些软件对数据进行处理。然而，这些软件默认采用的都是LS方法回归。本研究认为，在处理离群数据或者类椭圆数据时，LS方法效果并不理想。因此，在使用软件时，应根据体育数据的特征进行调整。本文对线性回归算法的讨论可以作为现有体育数据分析方法的一种补充。

[1]马勇占.应用线性回归法评价身体形态、发育水平的几个问题的探讨[J].中国体育科技,2002, 38(1):56-58.

[2]姚道迪.体育产业上市公司资本结构与经营绩效关系的实证研究[J].皖西学院学报,2013, 29(4):47-50.

[3]李传伟. Excel多元线性回归在体育统计学中的应用[J].中国管理信息化,2011(19):65-66.

[4]王旭辉,敖运忠. Excel 2000多元线性回归在体育教学中的应用[J].上饶师范学院学报：自然科学版,2005.

[5]朱红兵,何丽娟.在SPSS10.0中进行数据资料正态性检验的方法[J].首都体育学院学报,2004, 16(3):123-125.

[6]王丽丽,王增辉.应用SPSS软件对速滑直道技术足底峰值压强数据的主成分分析[J].吉林体育学院学报,2010(1):58-59.

[7]王大愚.最小二乘法平滑技术在体育中运用的尝试[J].体育科研,1984(6):14-16.

[8]权小娟,卢春天.青少年体育锻炼中的同伴效应及性别差异[J].上海体育学院学报,2020(4).

Three Methods of One-dimensional Linear Regression in Sports Data Analysis

HU Haitao, etal.

(Nanjing Forestry University, Nanjing 210037, Jiangsu, China)

江苏省高校哲学社会学一般项目《高校体育线上线下课程评价体系研究》（2021SJA0124）。

胡海涛（1981—），硕士，讲师，研究方向：体育数据分析。

喻孜（1981—），博士，副教授，研究方向：计算物理。