基于投入产出和影响因素双重视角的浙江省GDP 预测研究*

□朱天福 赵 静 张 琦 张 鹏 张崇辉 陈思超 陈思博

国内生产总值（Gross Domestic Product，简称GDP）是一个国家（或地区）所有常住单位在一定时期内生产活动的最终成果。它是衡量一国或地区经济状况、发展水平的重要指标（李宝瑜和张靖，2012）。目前各国政府的统计部门均把其作为描述经济发展最重要的宏观指标。GDP 不仅是制定经济发展战略和宏观经济政策的重要工具和参考依据。同时，它还能够对宏观经济政策进行检验，是反映政策科学性、合理性和有效性的重要手段。

随着经济发展，特别是经济发展的不确定性因素大大增加，如国际形势变化、贸易摩擦增加、大宗商品价格波动、新冠肺炎疫情影响等，需要对经济形势及时作出研究判断，以便及时制定经济干预政策，保障经济发展处于合理区间。因此，非常有必要对GDP 未来走势进行建模预测，提升预测预警和战略目标管理能力，为推进高质量发展建设共同富裕示范区提供统计支撑。

｜研究思路和创新点

（一）现有文献评述

整理相关文献可知，目前学术界就GDP 预测展开的大量研究，主要基于混频预测模型、时间序列模型和机器学习模型等展开。例如，张劲帆等（2018）构建了混频向量自回归模型，利用贝叶斯预测方法，对中国的宏观经济进行预测，结果表明房地产行业对中国宏观经济具有重要作用；仝冰等（2009）采用VAR 模型对宏观经济变量进行预测，并将之与朗润预测进行对比，发现货币无法预测未来经济活动；叶钰城（2021）讨论了技术创新与经济增长之间的关系，通过专利数据来衡量国家创新能力，并对各国人均GDP 的增长率进行预测。此外，何强等（2020）和熊志斌（2011）均采用机器学习模型对GDP 进行预测，并取得较高的预测效果。

但是，现有关于GDP 的预测研究大多基于单一视角开展，且使用的模型均具有限制性。例如，时间序列模型采用单指标的自回归，适用于经济发展较有规律且相对平稳的情况，对于出现新冠肺炎疫情等特殊事件后的预测结果不甚理想；机器学习模型的预测过程类似“黑匣子”，无法对预测结果进行合理解释；混频预测模型需要统计部门并不掌握的每日高频数据，数据获得性存在问题。事实上，GDP 作为一种宏观经济生产活动，其本质上还是一种基于要素投入的经济产出现象。因此，通过对GDP 的投入要素进行建模，能够较为准确地捕捉经济生产活动规律。此外，从GDP 核算的角度来说，统计部门在核算GDP 时往往会侧重于对GDP 产生重要影响的行业或者指标，故对GDP影响因素建模也能较为准确地反映地区经济形势。

（二）研究思路

本文基于投入产出和影响因素双重视角，采用C-D 生产函数模型和GDP 影响因素模型对浙江省GDP当季总量进行建模，通过对两个模型预测结果的相互验证以证明本文思路的有效性。而后在测算GDP 增幅时，假定预测期和最近季度的价格波动及产业结构基本相同，并结合GDP 当季现价总量预测值以及最近季度GDP 核算的缩减指数，即可推算得到GDP 同比增幅（考虑到GDP 数据的敏感性，本文仅作理论及思路探索，隐去具体模型及预测结果）。进一步地，通过对比本文提出的这两个模型与其他时间序列模型的预测结果，突出本文的模型不仅有较高准确性和可解释性，同时在突发情况下的预测效果更佳。

（三）创新点

一是采用统计部门便于掌握的基础数据建模。指标选择上更有方向性地选取了占GDP 比重较大的行业且易获得的相关指标，如基准化后的GDP 季度总量、规模以上（以下简称规上）工业和规上服务业等从业人员数、规上工业总产值等。二是充分利用GDP 核算实践经验，部分借鉴GDP 季度核算方案。如在数据处理上，交通运输周转量采用季度GDP 核算方案中的权重加权旅客运输量和货物运输量。三是先预测当季GDP 总量再根据最近季度的价格缩减指数推算GDP 增幅，预测GDP 增幅准确性更高，更加贴近经济运行实际。

｜模型构建及指标选择

（一）C-D 生产函数模型

1.模型构建。作为最典型的生产函数，柯布-道格拉斯（Cobb-Douglas）生产函数（简称C-D 生产函数）对于测算技术进步，分析规模经济、最佳投入结构等问题具有重要作用。其基本形式如下所示：

式中，A 是技术进步水平，具体包括生产技术、工艺设备、人工能力和管理水平等因素。K 是资本要素，可以是投入的资金额或投入的设备等固定资产数额。L 是劳动要素，即所投入的劳动量。α 是资本K 的产出弹性，β 是劳动L 的产出弹性，μ 为随机干扰项。Q 是产出量，可以为实物形式的产出量，也可以作为价值形式的产出量。

2.指标选择。根据宏观经济投入产出的思想，国民经济生产活动产出要素的主要表现形式为GDP，而投入要素主要包括人力（劳动力）、物力、财力（资本）、技术等（表1）。

表1 C-D 生产函数模型的变量及解释

其中，劳动力指从事增加商品价值的有用劳动能力，是蕴藏在人体中的脑力和体力的总和。根据数据的准确性以及可获得性，本文选择规上第二产业从业人员（包括规上工业、规上建筑业从业人员）、规上（限上）第三产业从业人员（包括限上批发零售业、限上住宿餐饮业、限上房地产开发业、规上服务业从业人员）等指标作为劳动力投入要素的备选指标。

物力包括可供使用的企业用地等经济资源，还包括树木、水资源、用电等自然资源。这些要素中，企业用地一经获取便基本不再变动，而宏观经济则呈周期性波动，甚至于在某些特定行业（如数字经济行业），企业不需要土地或者仅需要小部分土地，便可创造出巨大的社会价值。由此，难以通过企业土地捕捉宏观经济的变化规律；树木、水资源等要素则相对集中于资源密集型行业，不具备典型性；与全社会用电量相比，工业用电与工业生产直接相关，与宏观经济走势拟合度更高。因此，本文选择工业用电作为物力投入。此外，供应链物流已成为影响国民经济效率的重要因素，本文选择运输量（包括铁路、公路、水路）、周转量（包括铁路、公路、水路）等能反映供应链运转能力的指标作为物力投入的补充要素。

资本指在宏观经济生产过程中所需的资金投入，本文选择本外币存款余额和本外币贷款余额（包括境内贷款和境外贷款）指标。

技术投入要素中，R&D 研发投入能较好地反映一个国家或地区用于投入技术研发的水平。

（二）影响因素模型

1.模型构建。多元线性回归模型是影响因素分析方法中最常见的一种方法，多元线性回归模型是指在相关变量中将一个变量视为因变量，其他一个或多个变量视为自变量，建立多个变量之间线性或非线性数学模型数量关系式，并利用样本数据进行分析的统计分析方法。多元线性回归模型的形式如下：

其中，y 为因变量，xi为自变量，即影响因变量的因素。βi为影响系数，α0为截距项。

2.指标选择。根据浙江现有GDP 行业结构，规上工业增加值是影响GDP 最重要的指标，但是规上工业增加值和GDP 存在高度共线性。因此，本文采用规上工业总产值进行代替（表2）。

表2 影响因素模型的变量及解释

规上服务业营业收入包括交通、信息传输、租赁和商务服务业、科学研究、水利、居民服务、教育、卫生、文化体育和娱乐业9 个门类，物业管理、房地产中介服务、房地产租赁经营和其他房地产业4 个中类的营业收入，所涉行业增加值占GDP 比重在25%左右，营业收入能较好地反映服务业发展趋势。

批发和零售业增加值占全省GDP 比重在12%左右，占比较大，一般用月度的限上批发和零售业销售额（全部批发和零售业销售额只有季度统计，并且需由国家统计局核定）来反映发展整个行业的发展态势。

建筑业增加值占全省GDP 比重约6%，用建筑安装投资能较好反映建筑业发展。

规上工业出口交货值和进出口总额作为衡量进出口规模的重要指标，反映企业通过生产经营实现的海外经济效益。但进出口总额不仅包含本地区企业创造的经济价值，还包含其他地区企业的产品，经由本地区售往海外而实现的经济价值，涵盖范围较广。而规上工业出口交货值则仅反映本地区规上工业企业产品销往海外所创造的最终价值，统计口径较为准确。综合考虑GDP的影响因素，本文将这两个指标也纳入建模范畴。

其他行业，如金融业，占GDP比重虽较大（8%左右），但主要指标本外币存贷款变化不大；公共管理业、农业相对稳定；住宿餐饮业增加值占GDP 比重不到2%，可忽略不计。

｜进一步分析

进一步地，为了突出本文的C-D生产函数模型和影响因素模型，本文将其与基于时间序列的3 个预测模型进行对比。

（一）时间序列模型

1.ARMA+GM 组合模型：是指基于ARMA 和灰色GM（1,1）的组合模型。根据表X 的结果，可得季节性序列和剥离季节项的GDP 序列。对于季节序列，经检验发现其满足平稳性过程，经过自相关和偏自相关检验后，发现序列满足3 阶拖尾和3 阶截尾，故采用ARMA（3,3）模型对季节序列进行拟合；对于剔除季节效应后的GDP 序列，考虑到其为递增序列，故采用灰色GM（1,1）模型进行拟合，并预测各期的GDP 值。

2.ARMA+Holt 组合模型：是基于ARMA 和Holt 指数平滑的组合模型。由于Holt 指数平滑模型适用于对含趋势项的时间序列数据进行预测，所以ARMA+Holt 组合模型的处理思路与ARMA+GM 组合模型类似，只是将ARMA+GM 组合模型中的灰色GM（1,1）方法替换成Holt指数平滑法即可。

3.Holt-Winters 平滑模型：是基于Holt-Winters 的指数平滑模型。该方法是一种经典的对含有季节项和趋势项的时间序列数据集进行平滑预测的单变量时间序列模型，如GDP 序列等。

（二）实证对比分析

图2 为各个模型从2014 年一季度到2022 年一季度全省GDP 当季总量的拟合结果，可以发现5 个模型的平均预测误差均在5%以内，具有较好的拟合效果。但是C-D 生产函数模型和影响因素模型在2021年一季度（受新冠肺炎疫情影响）的预测误差分别为4.19%和-0.5%，较时间序列模型而言具有较大的优势，表明这两个模型在突发事件下也具备了较好的拟合效果。

图1 GDP 序列及其分解结果

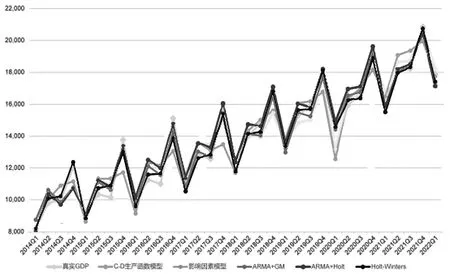
图2 各个模型的拟合结果对比

另外，从模型本身的特征来看，ARMA+GM 模型、ARMA+Holt 模型、Holt-Winters 模型属于单变量预测模型，其优点是结构简单，在常规状态下具有较好的拟合效果，但不足之处在于可解释性较差，且对突发事件的预测效果不佳；C-D生产函数模型是以投入产出要素作为变量，对GDP 进行拟合，是一种线性关系的模型；影响因素模型也是基于GDP 影响因素构建的线性模型。这两个模型的优点是模型简单、解释性较强、较为直观，相较时间序列模型而言对突发事件具有较好的拟合效果。因此，在综合考虑后，本文选择C-D 生产函数模型和影响因素模型作为浙江省GDP 预测的主要模型。

｜结论及建议

（一）主要结论

本文基于投入产出和影响因素双重视角，采用C-D 生产函数模型和GDP 影响因素模型对浙江省GDP总量进行建模，通过对两个模型预测结果的相互验证以证明本文思路的有效性。进一步地，通过对比C-D生产函数模型和GDP 影响因素模型这两个模型与其他时间序列模型的预测结果与实际差距情况，突出本文构建的模型不仅有较高准确性和可解释性，同时在突发情况下的预测效果更佳且兼具统计特色。

（二）不足及建议

本文的研究仍存在不少不足之处，主要在于：第一，GDP 影响因素众多且相互关系错综复杂，本文中选择的指标大致能反映经济发展的趋势，但并不能涵盖所有的经济活动，无法完全准确地反映GDP 的具体核算结果；第二，GDP 预测模型中的主要相关指标预测采用单指标的时间序列模型，受限于时间及精力，预测方式相对简单，存在一定程度上的准确性问题；第三，根据规定，GDP 采用统一核算方式，当各省汇总的GDP 总量、增幅与全国GDP 存在较大差异时，国家统计局还将按照GDP 统一核算方案，以全国数据为准，对各省初步核算的GDP 数据进行衔接处理。根据模型测算出来的GDP 总量及增幅无法考虑GDP 统一核算因素，肯定会与实际值存在差异；第四，实际情况中，较难完全满足本文先预测GDP 当季现价总量，再根据最近季度GDP 核算的缩减指数推算GDP 增幅所隐含的假设，即预测期和最近季度的价格波动及产业结构基本相同。

为进一步完善GDP 预测模型，不断提高预测结果的准确性，有以下建议：

1.对GDP 影响因素模型中涉及的主要相关指标进行深度研究，选择采用更为精准的预测模型。

2.扩大基础资料来源，充分挖掘银联消费、港口货运量、机场客运量、网络购物等高频大数据，以及其他部门未公开的内部数据，构建灵敏度更高的混频预测模型。

3.尝试采用C-D 生产函数模型和GDP 影响因素模型同步预测全省和各设区市的GDP 情况，通过积累一段时间的预测数据及偏差情况，逐步完善预测模型。

4.预测期和最近季度的价格波动和产业结构可能存在一定偏差时，还需对最近季度的价格缩减指数评估后再用于预测模型。