林木子代试验中小区平均值法与转化分析法比较

叶金俊, 叶金水, 包小梅, 黄琳, 毛海淋

1. 遂昌县生态林业发展中心，浙江 遂昌 323300；2. 遂昌县自然资源和规划局，浙江 遂昌 323300

单株观察值法常用于处理林木统计学研究试验数据，不少学者[1-6]应用Monte Carlo（蒙特卡罗）模拟法，在试验数据不平衡或严重不平衡时，比较验证不同分析方法间的分析效果、优点和不足之处，分析其与方差分量估计法的优劣[1-2,7-9,10-12]。

林木田间试验由于外在环境及植物间竞争等因素，导致部分试验植株死亡，最终得到的是非平衡试验资料。按照传统的现代线性模型理论、方差分析等来处理这些非平衡的试验数据，常常获得负的方差分量，不能给出数学解释，同时也没有生物学意义，说明试验数据的分析方法可能有问题。2009年，齐明对林木正交试验设计的非平衡数据处理，提出了一个转化理论[13]，2014年，齐明采用计算机模拟，论证了转化分析法的统计学基础，并得出就同一非平衡数据，转化分析法无论是在随机模型，还是在固定模型上均优于Henderson方法I的结论[14,15]。但小区平均值法处理林木田间试验数据的现象仍然随处可见，并且数据量越大（如多地点多年度的试验数据），采用小区平均值法的频度就越高。知网文献检索结果显示:至2021年2月采用小区平均值法来处理林木田间试验的非平衡数据的文献多达8 943条。 林木遗传育种中，无性系材料的田间试验资料，可采用小区平均值法进行数据处理；林木遗传育种的正交田间试验数据，由于平衡不平衡（缺株）、规则不规则（缺区），宜以单株值进行转化分析法统计分析[13-14]。为系统地评估小区平均值法在处理林木子代试验非平衡数据中的优缺点，借助Monte Carlo模拟法，产生非平衡试验数据，以转化分析法分析结果为参照对象，评估了林木试验中小区平均值法的统计效率，分析精确性、参数大小和精度，比较研究了这两种方法在随机模型和固定模型条件下的分析后果: （1）着重评估数据处理方法能否达到田间试验的目的;（2）其统计分析的效率如何;（3）其统计分析的精确性如何。为选用正确而合适的统计分析方法和促进林木数量遗传学发蔚县提供科学依据。

1 模型与方法

1.1 平衡试验设计及其统计分析模型

从研究的普遍性、计算工作量的大小等方面考虑，采用单因素随机区组（RCB）设计。林木子代测定的田间试验中,小区的设计一般为4～6株小区、也有8或10株小区。以下五个试验，采用Monte Carlo法模拟。为体现研究性状内在的遗传变异幅度,采用了40个半同胞家系，每个试验分别产生100套数据:

（Ⅰ）40个半同胞家系，10个区组，4株小区参试；

（Ⅱ）40个半同胞家系，8个区组，5株小区参试；

（Ⅲ）40个半同胞家系，8个区组，6株小区参试；

（Ⅳ）40个半同胞家系，6个区组，8株小区参试；

（Ⅴ）40个半同胞家系，4个区组，10株小区参试。

1.2 平衡试验数据的产生

按照林木遗传育种的经验，假设半同胞家系间、区组重复、小区株间因子服从正态分布，指定株间变异的方差Ve、区组重复因子的方差Vb、半同胞家系的方差Vf分别为280、15 、20。

按原试验设计模式（即Henderson方法I）来模拟试验数据：处理与区组重复间的交互作用因子不遵循正态分布，绘散点图表明（FB）ij遵从二项分布，因此按二项分布产生其效应值。群体平均值为60。采 用Matlab7.X语 言[19,20]编 写 程 序,以 获取RCB设计的试验平衡资料。每个试验一次模拟共100套数据，保存至EXCEL文件。

1.3 非平衡试验数据的产生及统计分析

由于气候环境、造林技术和株间竞争等多方面因素对造林存活率有所影响，多年来林木测定调查结果为造林存活率多数在75%～95%，多片10多年生杉木试验林的平均保存率在83%。假设随机死亡的保存率为83%，通过MATLAB语言中设计的删除语句随机删除,获取非平衡试验数据。

1.4 不平衡试验数据的转化分析法分析

由于是正交试验，故每套资料先将多株小区转化为单株小区[13]，采用转化分析法建立如下线性模型：

其中： i = 1→40； j =1→40～48；k=1或0。u是群体平均效应；Fi是第i个家系的效应值；Bj是第j个区组重复的效应值；Eijk是株间变异；Yijk是第i个家系在第j个区组重复中第k个观察值。

在随机模型条件下，各参试因子都是随机因子。于是：

方差分析原理参见有关文献[13]。期望均方结构见表1。

表中的期望均方的调节系数k计算、非平衡数据的处理和参数估计见参考文献[13,14]。

1.5 不平衡试验数据的小区平均值分析法

使用Matlab7.X语言，编写以获得以小区平均值为单位,参与统计分析非平衡数据的程序。林木半同胞子代试验，以小区平均值进行统计分析时的线性模型为：

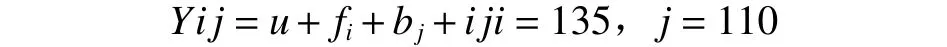
以小区平均值参与计算时，原试验变成了两因素无重复的方差分析模型，其期望均方结构如下表2。

根据表2中的结果，估算随机模型条件下，因子方差分量和家系遗传力；然后分析固定模型条件下，家系效应值的大小和秩的次序，以转化分析法的结果为参照物来分析小区平均值法的家系效应值产生的误差及选择产生的失误率大小。

表 1 单因素随机区组不平衡数据转化分析法的期望均方结构Tab. 1 Expected mean square structure of single factor random block non-equilibrium data in transformation analysis method

表 2 半同胞试验小区平均值法的期望方差结构Tab. 2 Expected variance structure of plot average method in half-sib experimental plot

在此模型中，半同胞家系遗传力为：hf2=σf2/[σf2+(1/b)Ve]

由于缺乏株间变异性信息，无法计算单株遗传力，许多文献采用如下公式：

上述公式中Ve为小区间的误差，故该计算公式结果有误。

1.6 以Monte Carlo模拟数据为基础的小区平均值法的结果评价

转化分析法：根据参试因子的调节系数和参试因子的方差分量，计算半同胞家系遗传力 Hf2和家系内单株遗传力hi2；小区平均值法：根据平衡模型,估计方差分量和家系遗传力。

根据100次Monte Carlo模拟结果，计算出若干参数的估计值，参数的偏差（偏差=估计值-参数真值）、偏差的显著性检验[1-2,7-9]。如果偏差的绝对值被其估计值除得的商，大于5%，可认为该参数有偏（Graybill & wortham，1956）。均方误差为MSE=Var（估计值）+偏差2。在相同参数情况下，均方误差越小，估计效益和精度越高[2,3-6,7-9,21]。

所有计算分析均在MATLAB7.0[19-20]和Excel 2003平台上完成。

2 结果与分析

2.1 随机模型条件下，小区平均值法的评估结果

（1）五个模拟试验中两种方法获得参试因子负方差分量的频率

五个试验的非平衡试验数据,林木转化分析法和小区平均值法的分析结果列于表3.

由表3可见, 五个试验的非平衡试验数据，林木转化分析法均未获得负的方差分量；而小区平均值法中，试验Ⅵ、Ⅴ中，区组因子分别有3%、6%的试验有负的方差分量。结果支持了转化分析法中参试因子是随机正态因子的观点。只有满足方差分析的正态性前提条件，才不会有负的方差分量[13,15]，同时表明转化分析法构建的线性模型是科学的、转化分析法优越于小区平均值法。

（2）几个参数效益的比较

在随机死亡的前提下，采用MATLAB语言的删除指令，将平衡的试验数据转变成不平衡的试验数据。用转化分析法来处理试验资料，计算小区平均值，再采用小区平均值法来分析试验数据，其结果列于表4～8。

试验‖转化分析法和小区平均值法的比较分析结果列于表4。

由表4可见，转化分析法的参数偏差不显著，小区平均值法中，误差方差、家系方差和区组方差偏性显著，且其均方误差也比转化分析法的误差大。

表 3 五个模拟试验中两种方法获得参试因子负方差分量的频率（%）Tab. 3 frequencis of negative variance component of the test factors obtained by two methods in five simulated experiments

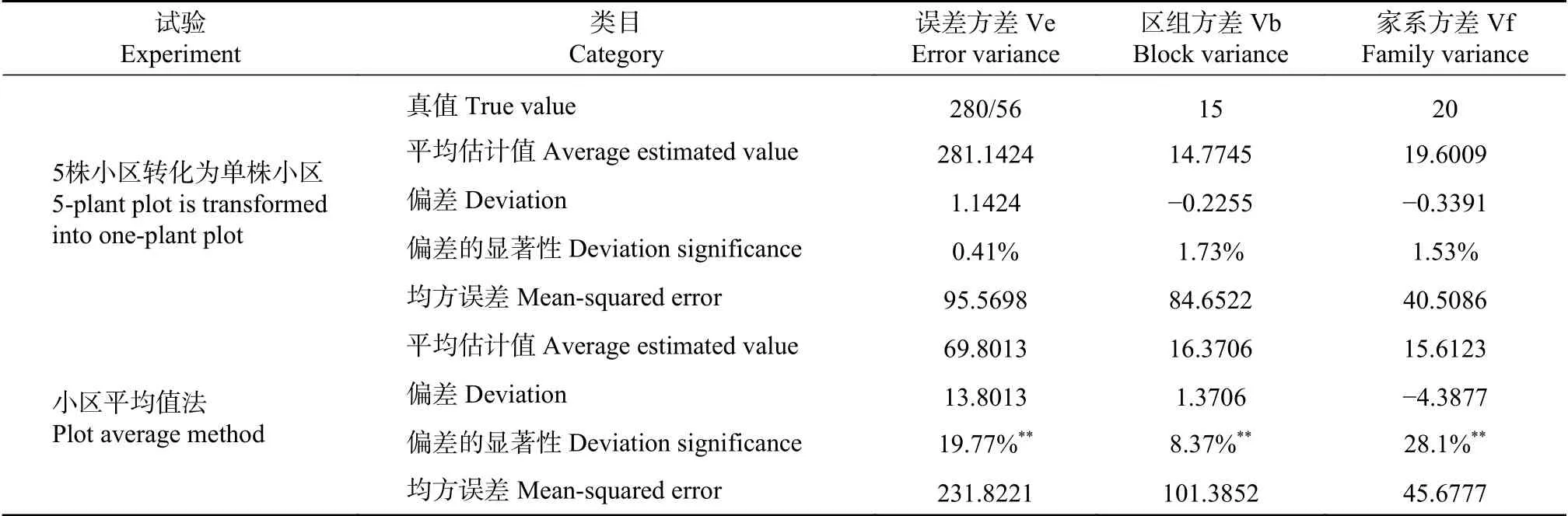
表 4 试验Ⅱ转化分析法与小区平均值法分析结果的比较Tab. 4 Comparison of analysis results between transformation analysis method and plot average method in experiment Ⅱ

试验Ⅰ转化分析法和小区平均值法的比较分析结果列于表5。

试验Ⅲ中,转化分析法和小区平均值法的比较分析结果列于表6。

试验Ⅳ中,转化分析法与小区平均值法分析结果的比较列于表7。

试验Ⅴ中,转化分析法与小区平均值法分析结果的比较列于表8。

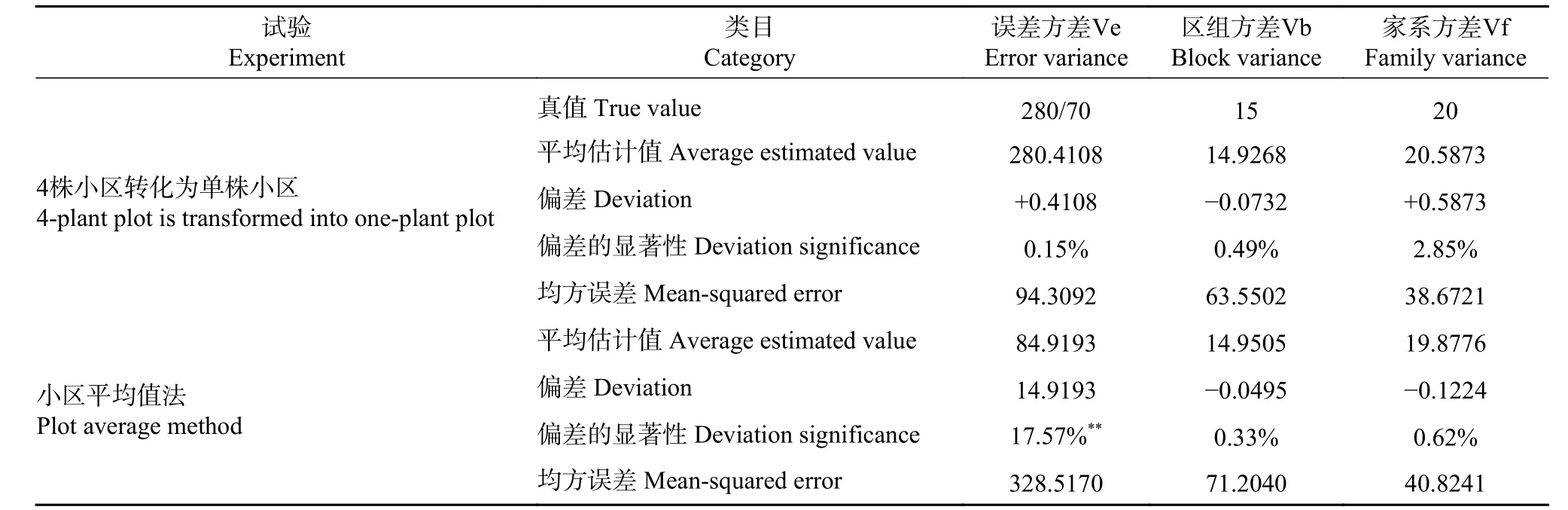
表 5 试验Ⅰ转化分析法与小区平均值法分析结果的比较Tab. 5 Comparison of analysis results between transformation analysis method and plot average method in experiment Ⅰ

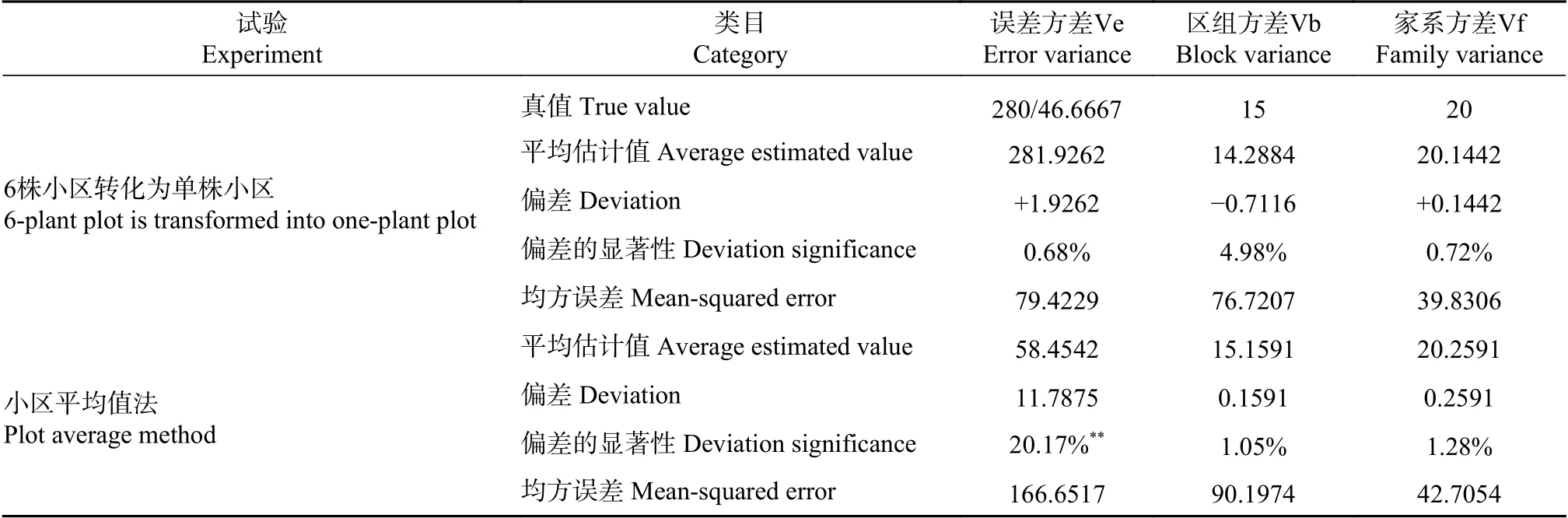
表 6 试验Ⅲ转化分析法与小区平均值法分析结果的比较Tab. 6 Comparison of analysis results between transformation analysis method and plot average method in experiment Ⅲ

表 7 试验Ⅳ转化分析法与小区平均值法分析结果的比较Tab. 7 Comparison of analysis results between transformation analysis method and plot average method in experiment Ⅳ

表 8 试验Ⅴ转化分析法与小区平均值法分析结果的比较Tab. 8 Comparison of analysis results between transformation analysis method and plot average method in experiment Ⅴ

从表5～8可见，转化分析法，各参数都存在一定的偏差，但均未达到显著水平，参试因子的方差分量估计值可认为无偏的。试验资料的小区平均值法，各参数也存在偏差，但只有表5～6中机误、表7中机误和区组、表8中机误和区组两因子的偏差达到显著水平，因此其估计值是有偏差的。进一步观察表5～8可见,参试因子的均方误差中小区平均值法都大于转化分析法，因此小区平均值法的参试因子方差分量的精度要比转化分析法小。

采用蒙特卡罗模拟法产生的非平衡试验数据，按照转化分析法和小区平均值法进行分析，其结果（列于表4-8）的变化趋势完全一致：试验资料的转化分析法，各参数都存在一定的偏差，但在这些偏差中，只有个别试验中，区组的方差分量偏差达到显著水平；而小区平均值法，通常区组和误差因子的偏性分析结果均显著。家系方差Vf 的均方误两者比较接近，对于Ve和Vb，转化分析法的均方误通常显著小于小区平均值法的分析结果。

比较表4-8中参数均方误差的相对大小，除家系遗传方差两者十分接近外，其它误差因子和区组因子的均方误差，转化分析法的结果均明显小于小区平均值法的均方误差，而均方误差的大小则表明该法参数估计效益的高低和分析结果精确性的高低，估计这种结果与区组数太少有关[2-6]。

（3）小区平均值法获得的遗传参数评估

试验林在83%存活率的条件下，根据Ve、Vb、Vf的大小和调节系数的大小，可计算出理论上遗传力的大小。以此为参照物，对非平衡试验数据转化前后的实际遗传力进行评价，见表9。

从表9可见：（1）所有的试验，转化分析法的统计效率要比小区平均值法的的统计效率要高，利于逆向选择和前向选择；（2）转化分析法的分析精确性要高于小区平均值法，因为前者的（Mse/bn）^.5比后者要小；（3） 小区平均值法的家系遗传力比转化分析法的结果低，并且遗传力的相对误差在-0.36%到-6.91%间变化，不利于逆向选择。

表 9 转化分析法与小区平均值法遗传力的大小和精度比较Tab. 9 Comparison of heritability and accuracy between transformation analysis method and plot average method

综合以上研究，从参数的精度和统计效益上证明了林木中小区平均值法不及转化分析法的分析结果，在林木子代测定资料的分析中宜优先采用转化分析法。

2.2 固定模型条件下,小区平均值法的评估结果

在固定模型条件下，同一试验资料，以转化分析法获得的家系效应值为参照对象，分析了小区平均值法获得的家系效应值的大小，相对误差，秩变化及20%的入选率时，优良家系选择的失误率大小如下:

以转化分析法为参照对象，小区平均值法的家系效应值，将产生1.02%～7.08%的相对误差；小区平均数值法中的许多家系秩与这些家系转化分析获得的秩不一致；采取20%的入选强度时，逆向选择会产生1/8—2/8的失误概率。这一结果与以前的研究结果[13]相一致。

3 讨论与结论

林木遗传育种中，规则的、平衡的试验设计常常获得的是非平衡试验资料。由于林木遗传育种是以单株值作为操作程序，此时采用转化分析法具有优越性，小区平均值法更适合处理平衡规则的林木无性系田间试验数据，存在缺区时，还要用最小二乘法补平，这非常麻烦.据齐明（2009）利用9年生的杉木全同胞子代试验林资料（实生起源）的研究表明：当出现数据缺失时，转化分析法（即直接采用缺株分析），其分析结果造成的统计误差，比该资料用小区平均值法（用最小二乘法补齐数据）获得的分析结果的误差小[13]。

蒙特卡罗（Monte Carlo）模拟法，产生的非平衡试验数据（针对实生苗），其分析结果在4、5、6、8、10株小区试验中表明：（1）小区平均值法适合于平衡规则的数据，在处理林木试验非平衡资料时，尤其是存在缺区时，要用最小二乘法补平，这与转化分析法相比，更加麻烦；（2）相对于转化分析法，小区平均值法的计算量小，但没法获得单株的遗传变异性，即统计效率低，不利于前向选择；（3）由于小区平均值法获得的家系遗传力，其大小和精度要低于转化分析法，不利于逆向选择；（4）转化分析法在若干参数上的偏性大小和均方误大小，明显优于小区平均值法的分析结果，这说明林木中采用小区平均值法处理非平衡资料时，其参数的精确性不及转化分析法。

在处理林木正交试验非平衡数据时，由于小区平均值法的统计效率低，获得的参数精确性差，不利于逆向选择和前向选择，建议采用转化分析法来处理。