基于聚类分析的风电场风速-出力典型波动过程关联分析

程 林 ，贾一超，王吉利 ，柯贤波，韩华玲

(1.国家电网有限公司 西北分部，陕西 西安 710048；2.中国电力科学研究院有限公司，江苏 南京 210037)

0 引 言

随着风电机组容量增加，轮毂高度增高，风轮直径增大，传动链各部件质量也将增大。风轮旋转过程中会存在较大的转动惯量，输出功率并不能随着风速的变化而实时变化，具有一定程度的滞后，且风速的小波动可能会引起功率的大波动，造成电能质量下降，影响电力系统的安全性和稳定性[1-4]。因此，对风速和功率的波动进行关联特性分析是十分必要的，研究风速不同波动过程下其对应的风电功率的波动情况，对提高风电功率预测精度和构建风电功率时间序列模型具有重要的参考意义，同时实现对风电功率预测的不确定性进行评估。

目前，风电功率预测方法大概可分为3种：物理方法[5-6]、统计学方法[7-8]和人工智能方法[9-10]。其中，物理方法是根据数值天气预报中的风速、风向等信息，根据风电功率曲线将风速转化为输出功率[11]。但由于实际并网运行的风电机组出力与风速是非线性映射关系，部分学者选择对风速与风功率波动特性进行研究。

大部分学者对风速与风功率波动进行概率分布建模：文献[12]对比了3种概率分布模型拟合风电场功率波动的效果，得出Laplace拟合效果最佳；文献[13]从相关性和平滑性两个方面，研究了不同时空尺度下风电出力波动性的统计学规律，并提出混合高斯分布进行概率分布分析；文献[14]提出一种基于非参数核密度估计的风功率波动性概率密度建模方法；文献[15]提出FLM 模型描述风场功率波动特性，并分析在不同时空尺度下的风功率波动情况。上述文献虽然对风速与风功率波动的概率分布模型进行了研究，但并未进行风速与风功率波动过程划分，只是针对单一时间点进行分析，并不能有效地为风电功率预测提供支持。

近年来，学者们发现传统的波动性研究着眼点侧重于单个时刻的风速或风电功率存在一定的局限性，因此波动过程已逐渐成为研究的新热点：文献[16]通过时序图简单分析了风速与风电出力波动过程；文献[17]考虑到风速波动与功率波动之间的匹配关系，提出基于波动过程的功率预测模型；文献[18-20]首先划分风电功率波动过程，然后得到了不同波动过程与预测误差的相关性；文献[21]同样针对不同的风电功率波动过程，建立对应的预测误差修正模型；文献[22]基于天气波动过程与功率波动过程的关联关系，建立了波动过程关联的短期组合预测模型。上述文献在风功率预测时考虑到了波动过程划分对风功率预测的影响，但并未专门针对风速与风功率波动进行研究。

综上所述，现有文献大多对风速、风功率等相关概率分布[23-24]进行研究，对风速或风电功率波动过程也有了一定的研究，验证了对风速和功率波动过程及关联特性分析能提高风功率预测精度。

不同波动过程的划分对关联性分析结果至关重要，聚类分析算法有严格数学基础理论，在面对各种线性与非线性数据时能够把一个数据集分割成不同的类或簇。因此，本文采用聚类算法对风速和功率波动过程进行划分，将风速和功率波动划分为5个不同的波动过程，对风速不同波动过程下的风速与功率波动量进行关联性分析。

1 波动过程的定义与划分

风电功率波动和风速波动的关系并不固定，对于风速波动的不同阶段，风电功率波动表现出不同的情况，因此需要首先对风速波动的波动过程进行划分，然后对比研究风速不同波动阶段对应的风电功率波动特性，分析对应的风速波动与风电功率波动之间的关联性。

1.1 定量描述波动过程

波动过程定义为一段时间内风速或风功率时间序列相邻时刻波动情况。以风速时间序列为例，1 h为1个时间段，每小时的波动情况为一个波动过程,波动过程如图1所示。

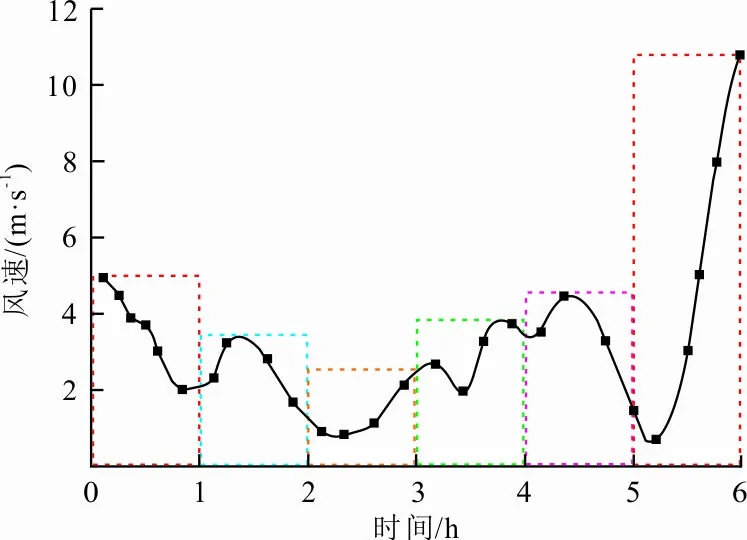
图 1 波动过程

为了能够划分不同的波动过程，需要定量描述风速波动，选取风速波动量Δvt和风速波动偏移量Avt作为描述风速波动的指标，以此为依据划分风速波动过程:

Δvt=vt+1-vt

(1)

(2)

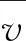
同样，选取风电功率所对应风电功率波动率ΔPt和风电功率波动偏移量APt作为描述风电功率波动的指标，并以此为依据划分风电功率波动过程：

ΔPt=Pt+1-Pt

(3)

(4)

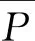
1.2 聚类算法划分波动过程

有了定量描述波动过程的指标，还需应用算法将相似的波动过程归类。聚类分析的基本思想就是根据规则对事物的某些特性进行归类，把具有相似性质的作为一类，使同一类的数据相似性大。常见的聚类分析方法有：K均值聚类算法、模糊C均值聚类算法、最大似然估计算法和基于图论的算法等。

其中，K均值聚类算法是应用最广泛的经典硬聚类算法。它进行优化时，目标函数常常用一个数据点到中心点的一个距离来表示，通过迭代运算获得最终结果[25]。硬聚类把每个待识别的对象严格地划分某类中，具有非此即彼的性质，而模糊C均值算法则是一种柔性的模糊划分，建立了样本对类别的不确定描述，更能客观地反映客观世界，从而成为聚类分析的主流[26]。

本文将分别采用这2种应用最广泛的聚类算法对风速波动和风电功率波动的波动过程进行划分，并对比2种不同聚类方法聚类结果是否存在差异。

1.3 波动过程划分步骤

步骤1：根据式(1)、(3)分别计算t时刻的风速波动量，风电功率波动量。

步骤2：以一个小时为一个数据单元，对每一个数据单元的3个风速波动量或3个风电功率波动量求平均值，作为衡量风速波动状况、风电功率波动状况的第1个指标。

步骤3：根据式(2)、(4)求得每个数据单元的风速波动偏移量、风电功率偏移量，作为衡量风速波动状况，风电功率波动状况的第2个指标。

步骤4：采用K均值聚类算法对风速波动量和风电功率波动量的平均值进行聚类，将其划分为①绕均值稳定波动、②上升波动、③下降波动3个波动过程。

步骤5：采用K均值聚类算法对步骤4所得①类波动过程以风速波动偏移量、风电功率波动偏移量为聚类指标进行第2次聚类，将①类波动过程划分为(a)稳定波动、(d)先上升后下降、(e)先下降后上升3个波动阶段。

步骤6：综合统计步骤4与步骤5的划分结果，最终将风速与风电功率波动过程分为(a)典型稳定波动过程、(b)典型上升波动过程、(c)典型下降波动过程、(d)先下降后上升波动过程、(e)先上升后下降波动过程的5大类，分别保存。

步骤7：采用模糊C均值聚类算法重复步骤5和步骤6，并分类保存。

2 算例分析

本文采用的数据为中国西北地区某风电场2016年1月1日至2020年12月31日的实际运行数据，时间分辨率15 min。该风电场满发额定功率为400.5 MW，运行5年平均发电功率73.12 MW，容量系数0.183。该5年内的风电场风速波动量、风电功率波动量的概率密度直方图及概率分布拟合情况如图2、3所示。

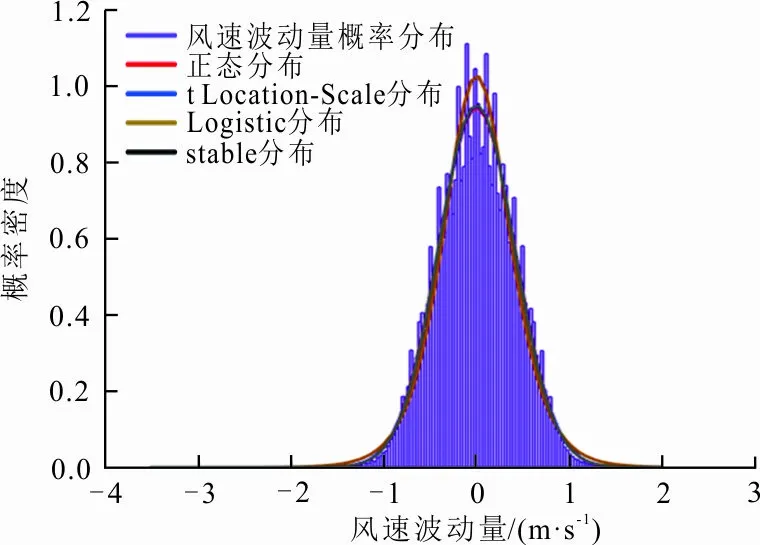
图 2 风速波动量的概率分布拟合

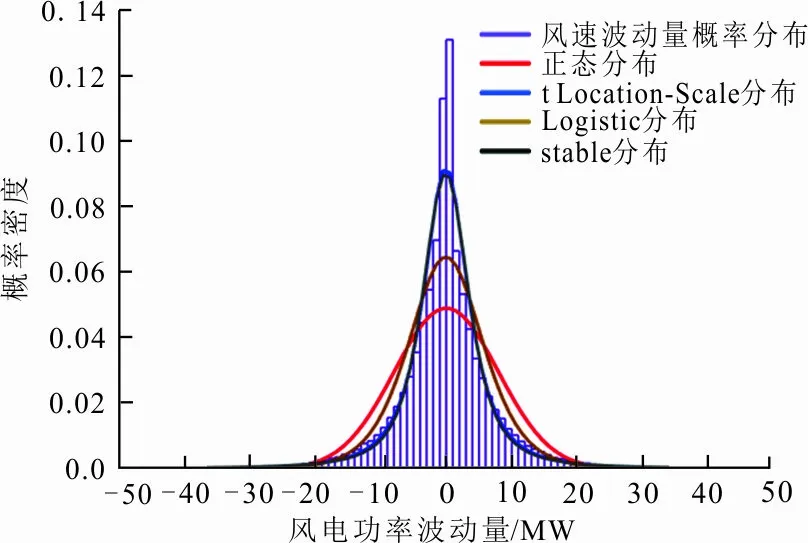
图 3 风电功率波动量概率分布拟合

虽然风电功率并不随着风速波动而实时线性波动，但从图2、3可以看出，风电场风速波动量、风电功率波动量的概率密度分布均可用t Location-Scale分布拟合，可知两者之间存在一定程度的关联性。

2.1 K均值和模糊C均值聚类算法聚类结果

K均值和模糊C均值聚类算法以每个数据单元风速波动量聚类指标的聚类结果见表1。

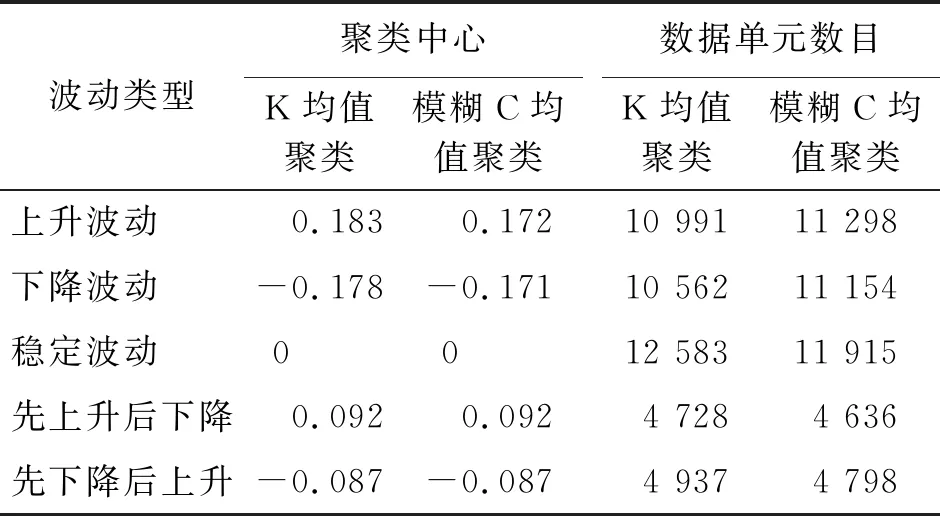
表 1 风速波动K均值/模糊C均值聚类结果

表1中，通过用K均值和模糊C均值聚类对每个数据单元的风速波动量平均值进行聚类划分，将风速波动粗略地划分为上升波动过程与下降波动过程，2个波动过程数据单元数目相差不多，但还存在大量绕均值波动的数据单元，需要进一步细分。进一步细分之后，可将绕均值波动的风速波动划分为稳定波动、先上升后下降和先下降后上升。稳定波动过程包含的数据数目与上升过程和下降过程相差不多，同时其余数据为先上升后下降和先下降后上升2个过程。

K均值聚类和模糊C均值算法以每个数据单元风电功率波动量为聚类指标的聚类结果见表2。

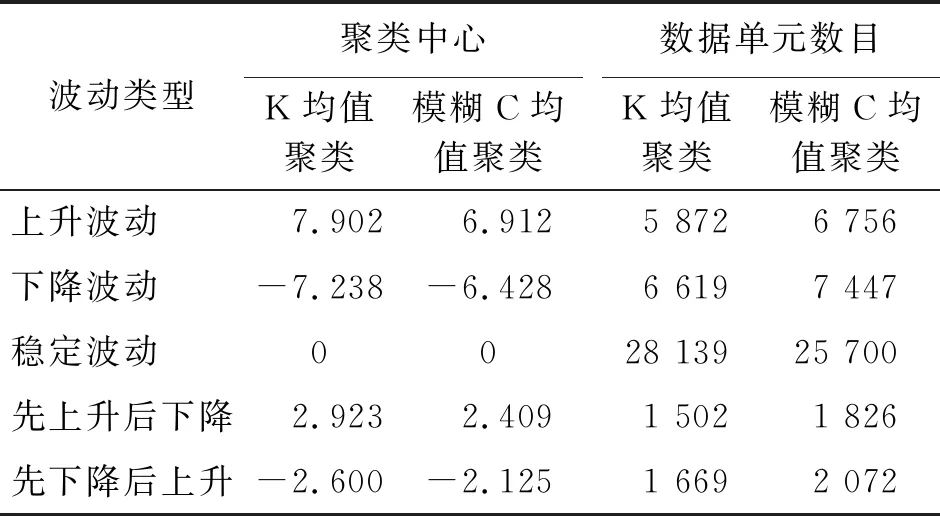
表 2 风电功率波动K均值/模糊C均值聚类结果

表2中，通过用K均值和模糊C均值聚类对每个数据单元的功率波动量平均值进行聚类划分，将功率波动粗略地划分为上升波动过程与下降波动过程，2个波动过程数据单元数目相差不多，但还存在大量绕均值波动的数据单元，需要进一步细分。进一步细分之后，可将绕均值波动的风速波动划分为稳定波动、先上升后下降和先下降后上升。功率波动稳定波动过程包含的数据数目仍然远大于其他类别，同时其余数据为先上升后下降和先下降后上升2个过程。

对比分析表1、2可知，K均值聚类算法与模糊C均值聚类算法在进行风速波动与功率波动划分时，K均值聚类算法将更多的数据聚类为稳定波动，而模糊C均值聚类的聚类结果更加均匀，将K均值聚类算法划分的稳定波动正确地划分到其他波动过程类型。

2.2 典型波动过程

2种聚类算法得到的波动过程基本一致，因此这里只展示其中一种聚类算法的结果，由K均值聚类算法得到的风速5种典型波动过程，如图4所示。

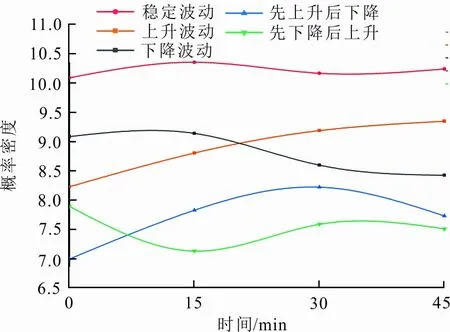
图 4 风速典型波动过程

从图4可以看出，风速波动的不同阶段有其明显的特征。稳定波动中，风速围绕10.2 m/s上下波动，从总体趋势上来看既不增大也不减小；上升波动过程中，风速波动过程中总体从8.3 m/s增大到了9.4 m/s；下降波动过程中风速在波动过程中虽然有略微上升的趋势，但保持风速减小的总趋势，风速从9.1 m/s减小到了8.8 m/s；先上升后下降与先下降后上升波动过程中，均存在一个极值，与过程起点或终点的风速差大于过程起止两时刻风速差。

3 风速波动与功率波动的关联性分析

本节选用皮尔逊相关性系数与灰色关联度2个指标评价风速与功率波动的关联性。相关性系数是一个经典的统计量，反映变量之间的线性关系。灰色关联度则反映两变量之间发展趋势的相似或相异程度，两者变化的态势(方向、大小和速度等)基本一致，则它们之间的关联度较大。

本文对K均值聚类算法和模糊C均值聚类算法所划分的风速波动不同波动过程下风速波动量与风电功率波动量进行相关性检验，结果见表3。

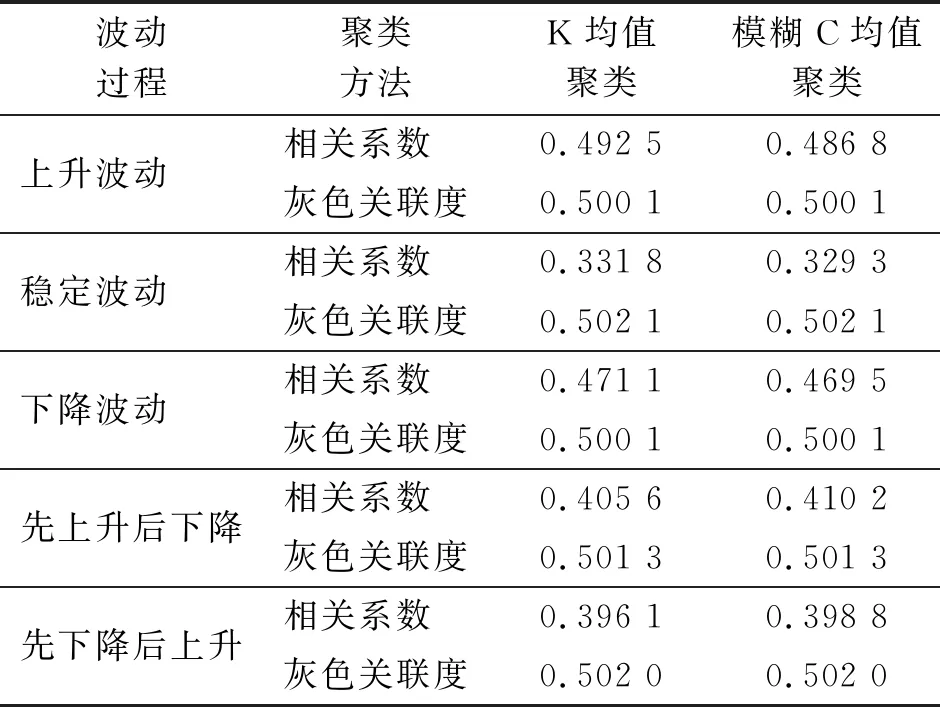
表 3 K均值/模糊C均值聚类风速波动过程下的关联性检验

从表3可以看出，基于2种聚类算法所得不同风速波动过程下的风速波动量与风电功率波动量相关性系数相差0.1，灰色关联度没有差别。其中，风速上升波动过程下两者波动量的相关系数最大，其次是下降波动过程，而稳定波动时相关系数最小。推测原因，可能是由于风功率随风速指数变化，即使当风速表现为平稳波动，风功率也会有较大波动。

所有风速波动过程下，灰色关联度差别不大，说明风速波动与功率波动趋势相似。

4 结 论

本文对风速和功率波动及关联特性进行了研究，定义5种风速波动和功率波动过程，通过聚类算法划分波动过程，分析了不同过程下风速波动量与功率波动量的关联性，结论如下：

1) K均值聚类与模糊C均值聚类结果有所差别，K均值聚类算法聚类中心之间距离较远，倾向于将数据归于绕均值波动的类别中，而模糊C均值聚类结果则比较平均。

2) 对比风速波动聚类结果和风电功率波动聚类结果，风电功率波动聚类结果更多的数据被归于绕均值稳定波动。

3) 基于2种聚类算法所得不同风速波动过程下的风速波动量与风电功率波动量相关性系数相差0.1，灰色关联度没有差别。

4) 风速上升波动过程下两者波动量的相关系数最大，其次是下降波动过程，而稳定波动时相关系数最小并且所有波动过程下，灰色关联度差别不大，功率波动与风速波动趋势相似。

但仍存在一些问题没有解决，比如风速波动与功率波动在几秒至十几秒的时间尺度下存在明显的滞后现象，限于数据的采样频率，本文并未对其进行深入研究；本文仅就风速波动与功率波动之间的关联性进行了研究，未能提出可行的方法对风电机组或控制系统方面的优化方案来提高二者之间的关联性；后续可以考虑针对以上2个方面进行深入研究。