具有轨迹偏移的自适应迭代学习控制

王守勤，贺兴时，耿 燕

(西安工程大学 理学院，陕西 西安 710048)

0 引 言

迭代学习控制(iterative learning control， ILC)是一种具有学习功能的高效控制方法，适用于具有重复运动特性的控制系统[1-2]。ILC通过学习先前迭代时的输入信息和误差情况，更新进入下一次迭代的控制输入，在有限时间内实现输出轨迹与期望轨迹的偏差趋于零[3-4]。自ARIMOTO等提出迭代学习控制理论后，引起了研究者的广泛关注[5]。为达到满意的控制效果，通常假设输入与输出间的参数矩阵是已知且不变的。然而在实际运行过程中，参数矩阵是未知且变化的[6-8]。为处理这种参数不确定的情况，学者们开始从自适应角度来设计迭代学习控制策略，从而形成了自适应迭代学习控制(adaptive iterative learning control,AILC)理论[9-11]。

一方面，传统的D-型(derivative-type)、P-型(proportional-type)及最优ILC要求期望轨迹在系统运行过程中沿着迭代方向严格重复[12-15]。期望轨迹作为系统跟踪的参考对象，其性能很大程度上影响了系统跟踪的难易程度。在跟踪过程中，由于噪声、环境、气候等因素，会出现输出跟踪难度大、轨迹偏移等问题。如何解决轨迹偏移问题并提高系统的跟踪性能，是一项极具挑战性的难题，目前这方面的研究甚少。文献[16]针对含有未知不确定参数的非重复线性离散系统，提出一种迭代学习控制策略，实现了系统的跟踪任务。然而，算法的收敛条件仍依赖于系统参数矩阵的对角元素的精确信息。文献[17]研究了迭代学习控制系统在期望轨迹偏移时的输出跟踪问题，提出一种鲁棒自适应迭代学习控制算法。但是，只有当所有系统参数都收敛时，才能实现该算法的收敛性。文献[18]通过最优化目标函数设计ILC控制器，给出了一种自适应迭代学习算法处理期望轨迹批量变化问题。然而文章所描述的期望轨迹依赖于参数矩阵的精确信息。如果文献[16-18]中的系统参数信息未知或不可用，那么所设计的ILC策略将失去意义。不仅系统的收敛性条件无法满足，而且系统输出对偏移的期望轨迹的跟踪也无法实现。另一方面，D-型、P-型等传统的ILC控制策略的收敛性条件都依赖于精确的系统模型参数(或矩阵)。值得注意的是，最优ILC算法不仅收敛性条件依赖于精确的模型信息，学习控制律的构建也依赖于精确的模型信息。

本文针对参数未知的单输入、单输出离散时变系统，分析ILC算法在期望轨迹偏移的情况下的鲁棒性能。首先，通过最小化实际输出与估计输出之间的误差设计参数自适应算法；其次，将估计的系统下三角参数矩阵和偏移的轨迹信息引入到ILC算法的构建中。最后通过数值仿真验证所提AILC算法的有效性。

1 问题描述

考虑下述单输入、单输出的线性离散时变系统：

(1)

式中：TN-1={0,1,…,N-1},TN={1,2，…,N};k∈N+，为系统迭代运行的次数；t为离散时间；uk(t)∈R和yk(t)∈R分别为系统的单输入和单输出向量；xk(t)∈Rn为系统的状态向量；A(t)、b(t)和c(t)分别为具有恰当维数的参数矩阵。为了方便文章的叙述与说明，将系统的期望轨迹设为rk(t)，随着迭代次数的增加而发生变化。

为了进一步的讨论，将输入uk(t)、输出yk(t)用超向量形式表示，即

yk=(yk(1),yk(2),…,yk(N))T

uk=(uk(0),uk(1),…,uk(N-1))T

因此，系统(1)可改写为

yk=Puk

(2)

式中：矩阵P是由A(t)、b(t)和c(t)形成的下三角参数矩阵，即

记为

将矩阵P中的下三角部分用不同维数的向量pi∈Ri表示，即

p1=p11，p2=(p21,p22)T，…，

pN=(pN1,pN2,…,pNN)T

综上所述，系统(2)可转换成向量形式:

(3)

由于系统参数信息未知，导致参数矩阵P和向量pi未知。然而,传统的P-型、D-型ILC算法的收敛性条件依赖于部分参数信息。本文考虑利用参数矩阵P的估计信息代替精确值，减少ILC收敛或鲁棒性条件对参数信息的依赖性。

假设rk=(r(1)+Δrk(1),r(2)+Δrk(2),…,r(N)+Δrk(N))T是具有不确定性的期望轨迹，迭代学习控制的目标是产生控制输入序列{uk+1}驱动系统(2)(或者(3))，使得输出轨迹随着迭代次数的增加尽可能快地跟踪上期望轨迹rk。为了进一步讨论，考虑如下假设成立:

假设1参数矩阵P是非奇异的。

假设2参数矩阵P是有界的。

假设3期望轨迹rk是有界的。因此，存在常数h，使得∀k∈N+，有‖rk‖2≤h成立。

2 自适应迭代学习控制机制设计

(4)

(5)

式中：μ>0,是权重因子。

(6)

(7)

引理1[19]A、B、R、Y和X分别是适当维数的矩阵。若矩阵A、B和R都是非奇异的，A-1已知，且已知矩阵B=A+XRY，则矩阵B-1可由式(8)获取：

B-1=A-1-A-1X(R-1+YA-1X)-1YA-1

(8)

根据引理1，易得

(9)

(10)

(11)

针对自适应迭代学习控制系统的轨迹偏移问题，考虑通过目标函数(12)获取迭代学习控制策略：

(12)

对目标函数(12)关于uk+1求偏导，并令偏导数为零，得到控制输入的更新策略为

uk+1=uk+(PTP)-1PTζk=uk+P-1ζk

(13)

式中：ζk=rk+1-yk。

(14)

3 收敛性分析

(15)

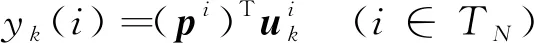
(16)

对式(15)两边同时取2-范数，并将式(16)代入其中，可得

(17)

(18)

根据式(17)和(18)，可得

(19)

将式(19)依次迭代进行下去，可得

(20)

证明根据跟踪误差的定义ek=rk-yk，可得

(21)

(22)

在式(22)两侧取2-范数，可得

(23)

由假设3可知，∀i∈{1,2,…,k}，存在正整数N1，当k>N1时，有

‖Δri‖2=‖ri-ri-1‖2≤2h

(24)

(25)

(26)

式中：0

由定理1的结论可知，存在正整数l，当k-m>N2时，有

(27)

利用范数不等式性质及式(27)，可得

(28)

(29)

根据式(25)、(26)和式(29)，当k-m>max{N1,N2}时，有

(30)

式中：d1+d2

将式(24)、(30)代入式(23)，可得

(31)

从而当k→∞时，可得

(32)

因此输出误差ek是有界的。

4 数值模拟

为了分析所设计的自适应迭代学习控制算法在轨迹偏移问题中的有效性，考虑利用文献[20]的一个线性离散系统的实例进行仿真。该线性SISO离散系统模型描述为

(33)

式中：t∈TN，t的最大值为N=200。选取迭代变化的期望轨迹为

(34)

式中：m(k)是在区间[-0.03,0.03]上均匀分布且迭代变化的随机数。m(k)的迭代变化情况如图1所示。

图 1 随机变量m(k)的迭代变化

为了更清晰明了地展示本文所描述的AILC方案的效果，考虑将其与经典的P-ILC算法(35)的跟踪性能

uk+1=uk+γek

(35)

进行比较。式中：ek为输出误差；γ为学习增益。图2为本文所设计的AILC算法与学习增益γ=0.2和γ=0.5的P-ILC算法的跟踪误差对比结果。

图 2 AILC与P-ILC的‖ek‖2对比

从图2可以看出：随着迭代次数k的增加，跟踪误差的范数都是逐渐减小并趋于零。值得注意的是，AILC曲线下降的速率最快。表明相对于γ=0.2和γ=0.5的P-ILC算法，本文设计的AILC算法的跟踪性能更好。

图3(a)和图3(b)分别描述了具有轨迹偏移的自适应迭代学习控制算法的第二次输出和第六次输出情况。从图3可以发现：虽然期望轨迹沿着迭代轴不规律变化，但随着迭代次数的增加，仍然能够在有限时间区间内实现系统输出对期望轨迹的完美跟踪。体现了本文所设计AILC算法的有效性。

(a) AILC算法的第二次输出

图4展示了AILC算法的跟踪误差随时间轴和迭代轴的三维变化图像。从图4可以发现，跟踪误差逐渐减小并趋于零。进一步说明了本文所设计AILC算法的有效性。

图 4 具有轨迹偏移的AILC算法的跟踪误差

5 结 语

针对轨迹偏移的迭代学习控制系统，通过设计参数自适应更新算法解决参数未知的问题。利用参数矩阵的估计信息和轨迹偏移的期望轨迹信息设计自适应迭代学习控制算法。通过理论分析证明了参数估计误差的有界性，保证系统跟踪误差有界且具有较好的跟踪精度。仿真实验证明了本文的自适应迭代学习控制策略在轨迹偏移时的有效性。