以CPI指数和GDP平减指数衡量货币供给量对英国通货膨胀的影响

林汝星

(谢菲尔德大学 经济学院，英国 谢菲尔德 S10 2TN)

1 研究意义和目的

全球通胀日益严重，各国政府相继采取控制货币供给量的紧缩性货币政策，以抑制价格水平上升，达到稳定有效地治理通货膨胀的目的。因此，为了准确有效地衡量货币供给量与通货膨胀率之间长期和短期相关性，理论分析和实证检验都是必要的。

在经济领域，关于通货膨胀的原因和性质以及相应的政策已经形成了比较完整和系统的理论，大致有两种观点：相关性是存在的和相关性是值得怀疑的。笔者查找了相关文献研究，认为两者分歧的主要原因是不同的样本区间和不同的建模方法。总体而言，货币供给量是长期影响通货膨胀的主要原因。因此，笔者尝试探究以CPI指数和GDP平减指数衡量的货币供给量对英国通货膨胀的影响。

2 研究方法

2.1 数据选择

选取英国货币供给量(M4)、英国消费者价格指数(UKCPI)和英国GDP平减指数(UKGDP)的季度数据，从1970年第一季度到2020年第四季度，记为1970q1到2020q4。

英国CPI指数和GDP平减指数数据来自圣路易斯联邦储备银行(Federal Reserve Bank of St. Louis)，基准年价格水平为2015年。M4的数据来自英格兰银行(Bank of England，BoE)。

本文分别对三个变量的自然对数进行取值，以减轻波动幅度造成的影响并消除时间序列数据中的异方差，从而得到三个时间序列：LM4、LUKGDP和LUKCPI。

2.2 模型选择

(1)

通货膨胀和价格水平是稳定的，只有货币供给量可以长期影响通货膨胀，因为它比其他变量更直接地影响价格水平。

(2)

货币供求平衡时，均衡价格水平由外生货币供给量决定，即由中央银行控制。因此，在M增长率固定的长期均衡状态下，i是固定的：

(3)

其中，π是通货膨胀率，ηY是货币供给量的弹性。由于ηY的存在，货币供给量的增加将被部分吸收，而超出的部分便会引起通货膨胀。

M4的增加伴随通货膨胀率的上升，但当经济遇到冲击时，GDP平减指数的增长率比CPI指数的增长率呈现更大波动。2020年，COVID-19疫情席卷全球，英国GDP下降11.3%，GDP平减指数的增长率迅速波动了1%左右，而英国CPI指数的增长率则一直较为平稳。值得注意的是，LUKCPI和LM4的波动速度几乎相同。因此，可以认为LUKCPI对LM4的变化更敏感，M4和CPI指数之间更可能存在长期和短期均衡关系。

图1 1970—2020年LM4、LUKGDP和LUKCPI的变化及增长率的波动性

(4)

(5)

其中，Yt代表通货膨胀，Xt代表货币供给量。β1i和γ1i捕捉ΔYt相对于ΔYt-1和ΔXt-1的短期动态，μ1t是白噪声误差项。α1和α2反映了对协整关系值的调整速度。本文VECM模型被估计为一个VAR模型，使用OLS估计长期关系Yt=θXt+εt。

(6)

(7)

VAR(q)模型的一般方程如下，A0是截距系数；Ai是自回归系数；Et是误差项。

Xt=A0+A1Xt-1+A2Xt-2+A3Xt-3+…+ApXt-p+Et

(8)

3 研究过程

3.1 平稳性检验

本文使用Stata软件分别对三个时间序列进行平稳性检验(ADF检验)：描述自然波动的平均值(LM4、LUKGDP和LUKCPI)，描述自然波动增长率的一阶差分序列(DLM4、DLUKGDP和DLUKCPI)，以及描述增长速度的二阶差分序列(D2LM4、D2LUKGDP和D2LUKCPI)。

表1 ADF检验结果

续表

从表1可以得出，平均值时间序列以及一阶差分时间序列都不平稳，而二阶差分时间序列是平稳的。因此， LM4、LUKGDP和LUKCPI都是I(2)时间序列。

3.2 Johansen协整检验

3.2.1 LUKGDP和LM4之间的协整关系

根据滞后项长度分析决定使用VAR(6)和VAR(2)模型，因VAR(2)模型在跟踪检验和最大特征值检验中表现不显著，最终选择VAR(6)模型。

表2 LUKGDP和LM4的协整检验方程

从表2可以得出：

-LUKGDP+26.1789LM4-393.4015=0

(9)

LUKGDP=26.1789LM4-393.4015

(10)

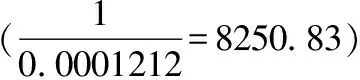
3.2.2 LUKCPI和LM4之间的协整关系

重复滞后期长度分析决定VAR(6)模型的选择，并且VAR(6)模型在跟踪检验和最大特征值检验中表现显著。

表3 LUKCPI和LM4的协整检验方程

从表3可以得出：

-LUKCPI+23.7634LM4-353.3308=0

(11)

LUKCPI=23.7634LM4-353.3308

(12)

3.2.3 LUKCPI、LM4和LUKCPI之间的协整关系

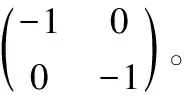
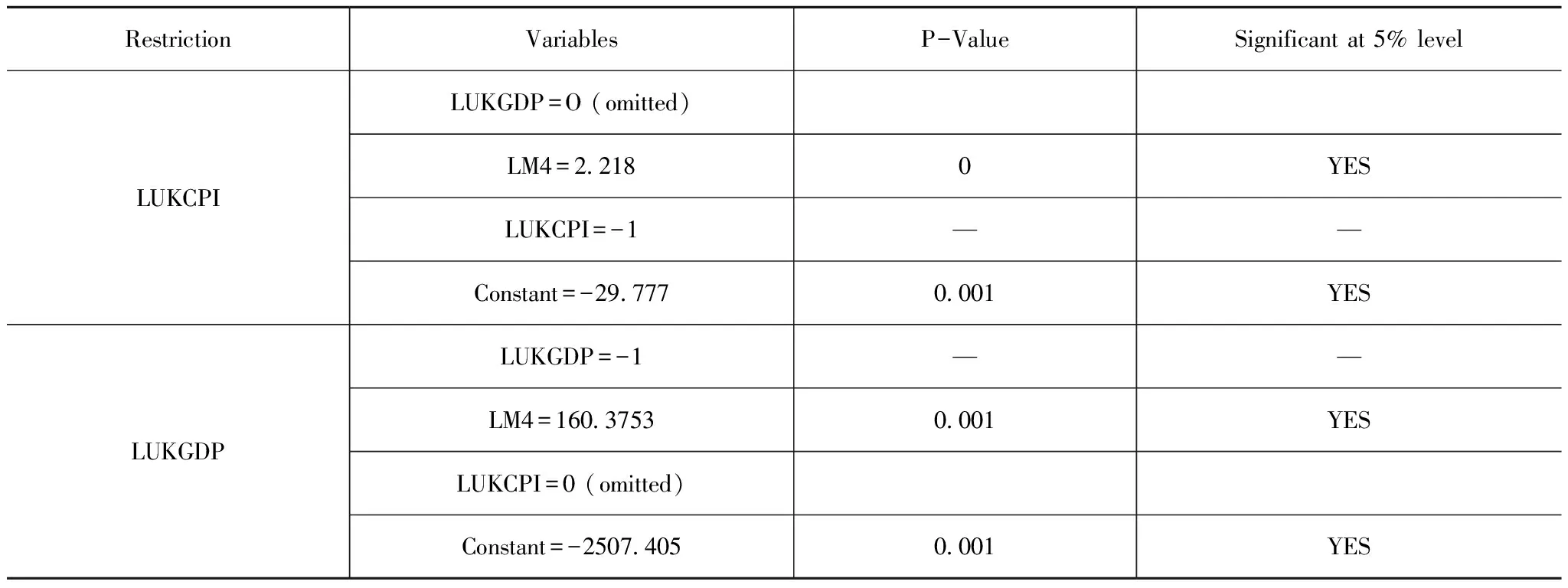
表4 LUKGDP、LM4和LUKCPI的协整检验方程

从表4可以得出：

-LUKCPI+2.218LM4-29.777=0

(13)

LUKCPI=2.218LM4-29.777

(14)

-LUKGDP+160.3753LM4-2507.405=0(15)

LUKGDP=160.3753LM4-2507.405

(16)

方程(14)中M4系数相对接近于1，这与相关经济理论结果一致。方程(16)中M4系数和常数值都很大，单位M4变化，GDP平减指数都有巨大差异和明显波动，在预测通货膨胀方面表现不佳。与之相比，CPI指数变化相对不受M4波动的影响。LUKCPI的调整速度参数为0.0099181，与LUKCPI的系数符号相反，表明单位时间LUKCPI的偏差将增加0.0099181。LUKGDP的调整速度参数为-0.0001211，符号与LUKGDP的系数相同，表明单位时间LUKGDP的偏差将减少0.0001211，低于CPI指数，即GDP平减指数对历史波动的反应不如CPI指数。换言之，CPI指数的波动趋势与M4的波动趋势更为相似，即CPI指数更加敏感和有效。

3.3 格兰杰因果检验

格兰杰因果关系被用来检验每个变量是否改善了另一个变量的预测，即该变量对其他变量的未来价值的预测能力。

表5 VAR(6)模型的格兰杰因果关系Wald检验

结果表明，M4的变化不是CPI指数和GDP平减指数的格兰杰原因，考虑M4历史值的基础上，M4变化的历史值不能改善对CPI指数和GDP平减指数的预测。然而，CPI指数和GDP平减指数都是M4变化的格兰杰原因，概率分别为96.5%和91.7%。综上所述，M4变化对引起CPI指数变化更明显也更敏感，更适用于预测通货膨胀。

3.4 SVAR模型和脉冲响应函数

在相关经济理论基础上，对上述VAR(6)模型施加进一步限制条件，生成结构性VAR(SVAR)模型来进一步识别LM4、LUKCPI和LUKGDP之间的因果关系。结果显示，GDP平减指数的R2=0.7456，而CPI指数的R2=0.8314，表明CPI指数在模型拟合程度上更优。

由于没有理论依据认为M4会受到GDP平减指数和CPI指数的同期影响。此外，GDP平减指数和CPI指数并不同时受到对方的影响，设定b12=b32=b13=b31=0。

(17)

因此，M4方程可以写成：

-0.2826LUKGDP+LM4+0.486LUKCPI=0

(18)

LM4=0.2826LUKGDP-0.486LUKCPI

(19)

为分析GDP平减指数和CPI指数如何应对M4的一次性正向冲击，生成脉冲响应函数，其中LM4是脉冲变量，LUKGDP和LUKCPI是响应变量。

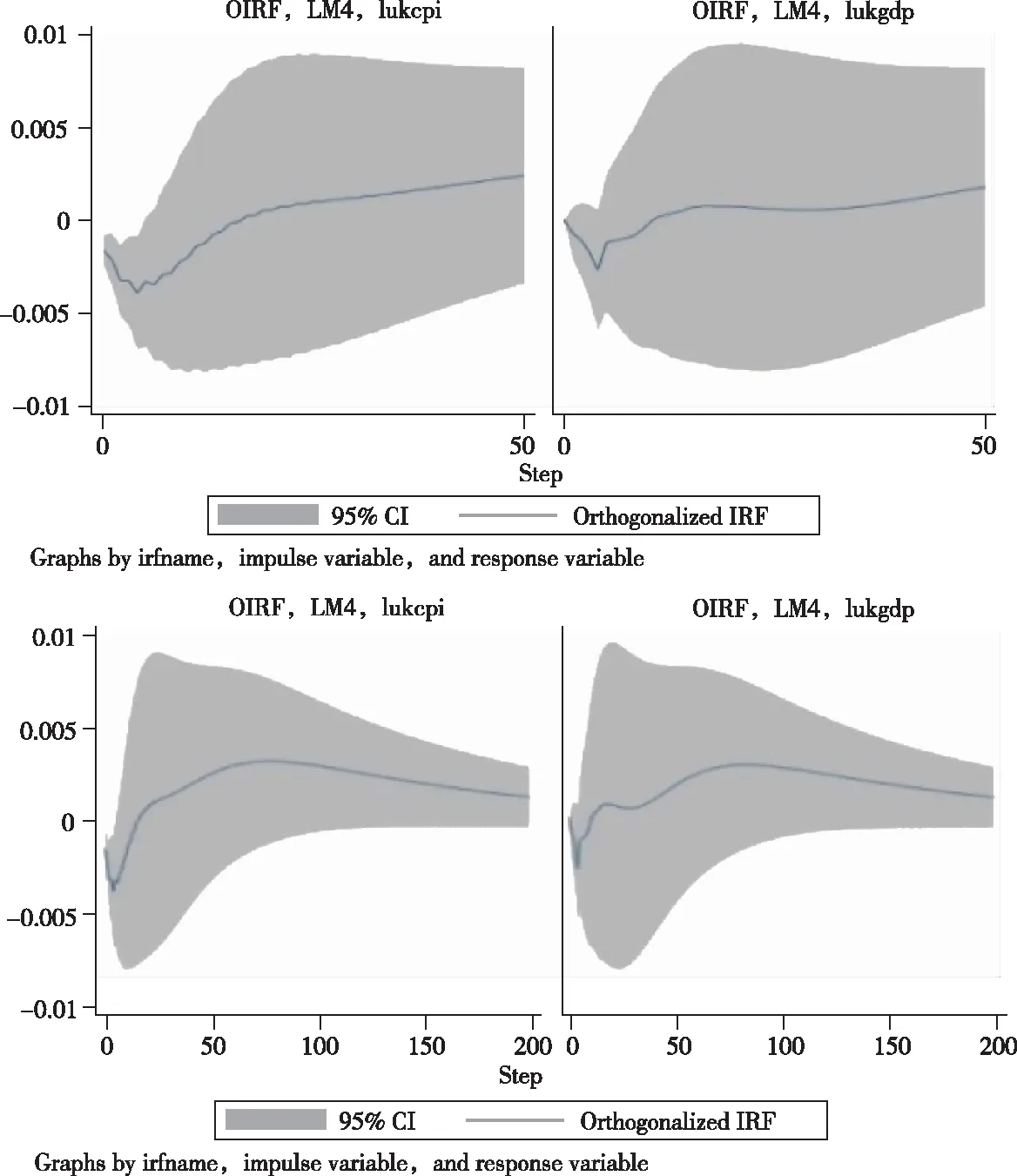
图2 50和200个季度的脉冲响应函数

从图2可以看出，CPI指数对M4冲击的反应从零季度开始下降并达到最低点。自第五季度，反应上升并逐渐趋于稳定。初始阶段，M4对GDP平减指数冲击反应趋近于零。但在后续十个季度，冲击影响急剧增涨并达到顶峰。总体来说，M4冲击对CPI指数有显著而长期的影响，而对GDP平减指数则是短期波动更为明显。因此，M4是长期调整CPI价格水平的一个更有效的变量，能够更有效地预测通货膨胀。

4 结论与建议

货币供给量和通货膨胀之间既存在短期波动效应，又存在长期均衡分布。从长期来看，货币供给量的增加与通货膨胀之间存在显著的正向协整关系。由于外部冲击，短期波动显著。如果货币供给量迅速增加，GDP平减指数的波动将超过CPI指数。因此，如果GDP的某个组成在短期内迅速上升，却没有引起价格水平变化时，GDP平减指数的波动将大于CPI指数，此时利用GDP平减指数预测通货膨胀可能会高估通货膨胀水平。除此之外，货币供给量的增加不能归因于通货膨胀率的上升，即通货膨胀率的上升或下降，并不会引起货币供给量的变化。

在实践中，应考虑结合使用CPI指数和GDP平减指数来更有效准确地衡量和预测通货膨胀水平。但是，GDP平减指数只能按年度或季度计算，不能及时反映价格波动，使其不适合用于短期波动预测。

在撰写本报告时，英国CPI通胀率(2021年第二季度)为3.2%，存在着持续高通胀的风险，促使英国央行实行更紧缩的货币政策。本文研究表明，监测货币供给量的变化并在短期内收紧货币政策可以帮助英国央行将通胀率带回目标。然而，本文是基于经济稳定的假设，没有考虑英国脱欧带来的影响，所以本文的结论并不完全适用于现阶段和未来英国通胀分析。

本文可以在以下三个方向上进行扩展。首先，虽然模型重点是英国通胀动态，但该模型对其他国家亦有借鉴性。其次，本文结果表明将英国的通货膨胀建模为经济政策不确定性函数模型是合理的，以有效反映英国脱欧影响和未来发展。最后，非线性模型在样本外预测通胀的能力是具有探究性的，需要未来更深入的探究。