异形拉伸弹簧的横向刚度及强度研究

唐嘉诚，黄志辉*，林柄宏，姜旭涛，陈坤亮

（1.西南交通大学牵引动力国家重点实验室,四川 成都 610031；2.广东恒力精密工业有限公司,广东 中山 528415）

拉伸弹簧是一种利用材料弹性来工作的机械零件，用以控制机件的运动、贮蓄能量、测量力的大小等[1-3]。米彩盈[4]提出了铁道车辆二系高圆簧横向刚度分析方法，并将理论分析结果与试验结果进行对比；李红艳[5]采用ANSYS 建立螺旋弹簧的几何模型，并对弹簧进行强度分析和疲劳寿命校核；钟文彬[6]利用有限元法和理论计算方法求解压缩弹簧的垂向、横向和弯曲刚度，发现有限元法可以更加准确快速得到弹簧各向刚度特性；周凯林等[7]基于ANSYS 建立了转向架一系圆柱压缩弹簧的几何模型，对弹簧的垂向刚度及横向刚度进行有限元分析计算，并与理论计算结果进行对比。对弹簧横向刚度的研究，目前所查阅到的文献都是以压缩弹簧为研究对象。本文以异形拉伸弹簧为研究对象，对其横向刚度进行研究，并分析了拉伸弹簧钩环位置对其强度的影响。

此异形拉伸弹簧为汽车座椅弹簧，用于汽车座椅靠背调节。实际使用时，该弹簧不仅承受轴向载荷，还承受横向载荷。本文针对其横向刚度和强度进行研究，并利用HyperMesh 与ANSYS 联合仿真进行分析和验证，还分析了拉伸弹簧不同钩环位置对其强度的影响，找到了应力最小位置，为进一步延长其工作寿命提供了参考。

1 异形拉伸弹簧的理论分析

1.1 异形拉伸弹簧的研究模型

此异形拉伸弹簧为圆柱螺旋弹簧。该弹簧中间段簧圈中径一致，两端部簧圈中径先增大后减小，各簧圈之间并紧无间隙，通过热处理和喷丸等工艺处理后消除应力，最后起耳完成整个结构，钩环偏置于弹簧同侧。其结构参数标注如图1 所示。异形拉伸弹簧的几何尺寸如表1 所示。表1 中：n为有效圈数；d为簧丝直径；D为弹簧中径；L1为钩环中心距离；R1为钩环半径。汽车椅弹簧两端簧圈中径均匀变化，弹簧最大簧圈中径为32.2 mm。弹簧材料采用SWP-B 琴钢丝，其材料属性如表2 所示。表2 中：E为弹性模量；ρ为密度；μ为泊松比；σs为抗拉强度。

表1 异形拉伸弹簧几何参数

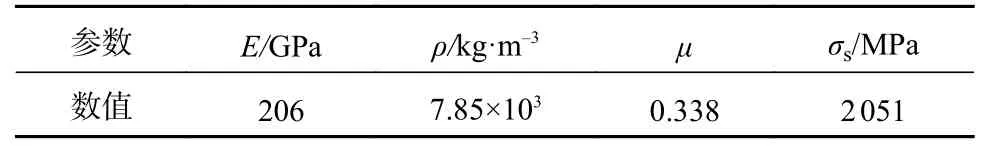
表2 SWP-B 琴钢丝材料属性

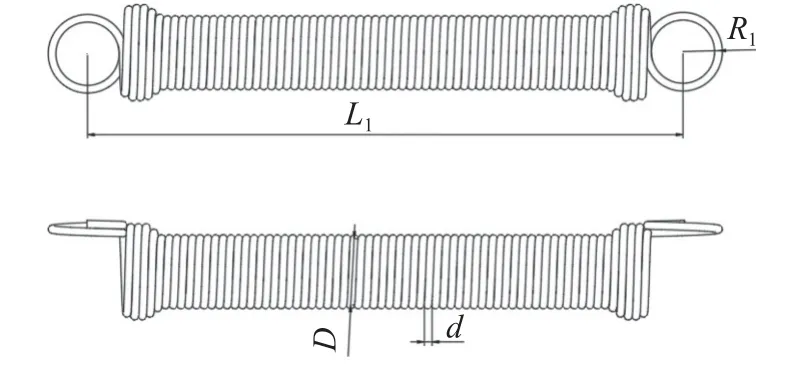
图1 异形拉伸弹簧结构参数示意图

1.2 异形拉伸弹簧横向刚度理论分析

将弹簧等效为一等截面悬臂梁，其等效弯曲刚度的理论计算公式[7]为

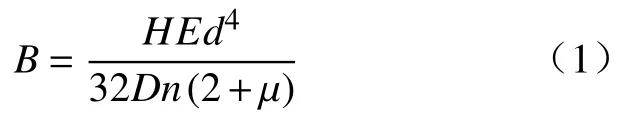
式中：B为弯曲刚度，N·mm2；H为弹簧工作高度，即受轴向载荷后的高度，mm。

该弹簧的轴向刚度为0.509 24 N/mm[8]，受到轴向工作载荷177.9 N 时，H为596.9 mm，将弹簧的参数代入式（1），计算可得弹簧的近似弯曲刚度B为61 600 N·mm2。

该异形拉伸弹簧受到轴向载荷与横向载荷时的受力简图如图2 所示，图中：F为轴向载荷；Fr为横向载荷；fr为弹簧最高点的横向变形量；z为弹簧任一点的高度；x为弹簧任一点至最高点的横向距离。

图2 异形拉伸弹簧受力简图

根据悬臂梁的挠曲线方程，可知

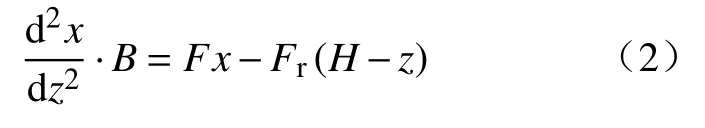
式中：F为轴向载荷，N；Fr为横向载荷，N；z为弹簧任一点的高度，mm；x为弹簧任一点至最高点的横向距离，mm。该方程的通解为

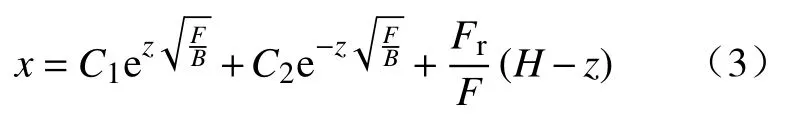
式中：e 为自然常数；C1和C2为比例系数，可由式（4）、式（5）确定。其边界条件z=0 时，=0；z=H时，x=0。

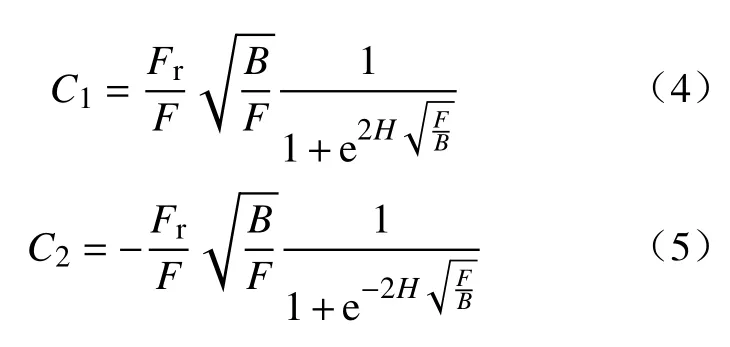
将式（4）、式（5）代入式（3），且当z=0 时，x=fr，从而得到拉伸弹簧在受到轴向载荷与横向载荷时的横向变形为

由式(8)可得，该异形拉伸弹簧的横向刚度为0.30763 N/mm。

2 异形拉伸弹簧的有限元分析

2.1 异形拉伸弹簧有限元模型的建立

本文通过CATIA 软件建立异形拉伸弹簧三维模型，将三维模型以stp 格式导入HyperMesh 中，对模型进行网格划分，赋予材料属性及单元属性。模型共包含节点147 700 个，单元110 754 个。在进行有限元计算前，对弹簧模型进行工况加载，即在弹簧的一端钩环处施加全约束，另一端钩环处施加不同大小横向载荷Fr和数值为177.9 N 的轴向载荷F，如图3 所示。

图3 异形拉伸弹簧受力及约束位置

2.2 异形拉伸弹簧横向刚度有限元分析

前处理完成后导入ANSYS 中进行多种工况有限元计算。笔者在有限元计算过程中发现，弹簧在仅受轴向载荷而未受横向载荷时，其受力端钩环仍产生轻微变形，如图4 所示。因此，在研究横向变形时，应减去不受横向载荷时产生的微变形。

图4 异形弹簧在仅受轴向载荷下的变形

不同的横向载荷对应的变形量如表3 所示。表3 中：Fr为横向载荷；x为横向位移，即考虑轴向载荷引起的钩环横向变形量；Δ为净横向变形量，即不考虑轴向载荷引起的钩环横向变形量。

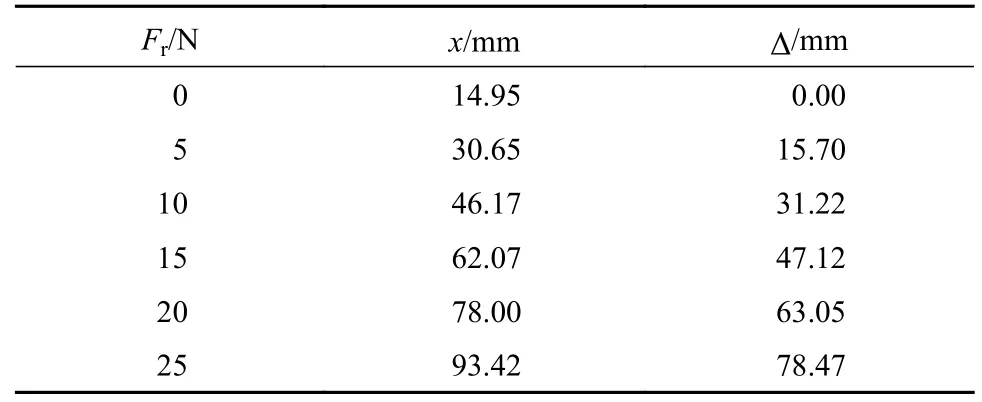
表3 异形拉伸弹簧横向载荷与净横向变形量

由表3 数据可得到异形拉伸弹簧横向载荷与净横向变形量的关系，如图5 所示。由图5 可知，该异形拉伸弹簧的横向载荷与净横向变形量之间呈线性关系，通过有限元分析得到横向刚度为0.318 58 N/mm，与理论计算结果相差3.4%，相对误差小于5%，从而验证了三维模型是有效的。

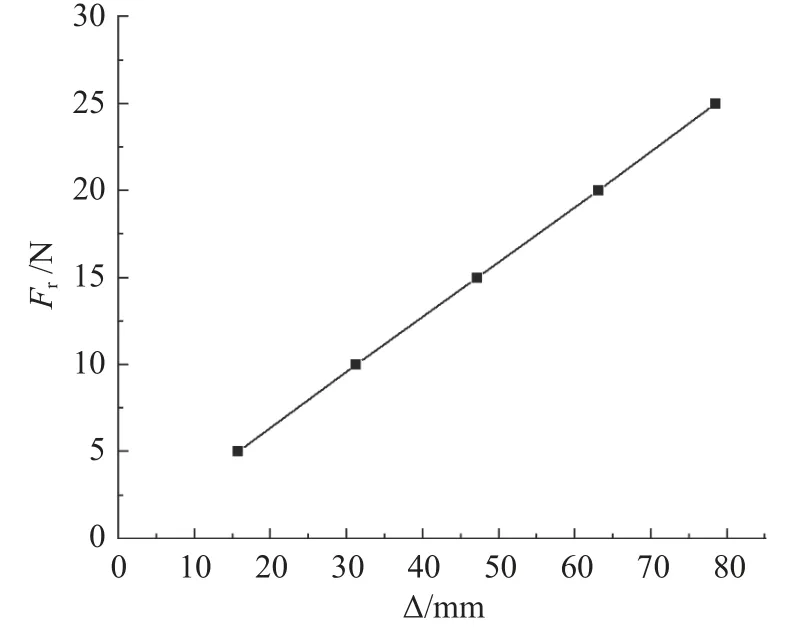
图5 横向载荷与净横向变形量关系

3 异形拉伸弹簧强度与寿命校核

该异形拉伸弹簧为汽车座椅弹簧，其实际使用情况是：安装工况为受106.2 N 的轴向载荷且其轴线与纵向成6°夹角；极限工况为受177.9 N 的轴向载荷且其轴线与纵向成10°夹角。2 种工况的剪切应力云图如图6 所示，安装工况剪切应力τmin为442.2 MPa，极限工况剪切应力τmax为720.8 MPa。

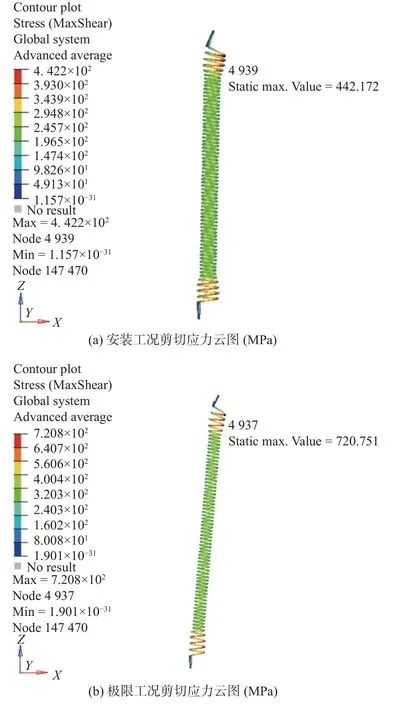
图6 2 种工况弹簧的剪切应力云图

3.1 异形拉伸弹簧的静强度校核

静强度校核的计算公式[9]为

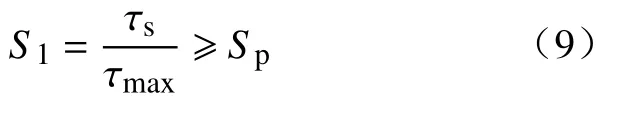
式中：S1为静强度安全系数；τs为抗扭屈服极限；Sp为许用安全系数，一般取1.3～1.8。

将参数代入式（9）计算，其中：查表[9]可知抗扭屈服极限τs=0.5σs=1 025.5 MPa，τmax为720.8 MPa。计算得到弹簧的静强度安全系数S1为1.42，满足静强度要求。

3.2 异形拉伸弹簧的疲劳强度校核

疲劳强度校核的计算式[10]为

式中：S2为疲劳强度安全系数；τ0为脉动疲劳极限。

将参数代入式（10）计算，其中，查表[9]可知，脉动疲劳极限τ0=0.35σs=717.85 MPa，τmax为720.8 MPa，τmin为442.2 MPa。计算得到弹簧的疲劳强度安全系数S2为1.46，满足疲劳强度要求。

3.3 异形拉伸弹簧的疲劳寿命校核

疲劳寿命校核的公式[11]为

式中：γ为循环特征，其计算结果为0.61。

4 钩环位置对其强度的影响

在异形拉伸弹簧的有限元分析过程中发现，在一端钩环施加全约束，一端钩环仅受轴向载荷的情况下，其受力端簧圈末端的中轴线会呈抛物线，与常规弹簧变形情况不相同。分析原因，可能是钩环位置导致的。为此，本文在钩环中置与偏置2 种情况对该弹簧等效应力和剪切应力的影响进行了仿真分析。

基于CATIA 建立的钩环偏置弹簧与钩环中置弹簧三维模型如图7 所示。将三维模型导入到HyperMesh 中进行离散，并将弹簧一端的钩环处施加全约束，另一端钩环处施加大小为177.9 N 的轴向载荷，最后将处理好的有限元模型导入ANSYS进行求解，2 组不同钩环位置的弹簧等效应力云图与剪切应力云图如图8、图9 所示。整理得到2 组弹簧的有限元计算结果如表4 所示。

图7 不同钩环位置弹簧的三维模型

图8 不同钩环位置弹簧的等效应力云图

由图8、图9 和表4 可知：钩环中置的弹簧相较于钩环偏置的弹簧最大等效应力减少327.23 MPa，降低18.54%；最大剪切应力减少87.6 MPa，降低12.21%。钩环中置的弹簧在仅受轴向载荷的情况下，其中轴线为一条直线，钩环偏置的弹簧在仅受轴向载荷的情况下，其中轴线末端呈现抛物线，且结合应力云图可知，钩环中置的弹簧受力更加均匀。所以，在安装位置允许的条件下，将弹簧的钩环位置中置能有效改善其受力情况，提高其强度安全系数，延长使用寿命。

图9 不同钩环位置弹簧的剪切应力云图

表4 2 组弹簧有限元计算结果

5 结论

1）基于悬臂梁理论推导的拉伸弹簧横向刚度与有限元分析结果较吻合，理论公式可有效计算拉伸弹簧的横向刚度。

2）该弹簧满足实际使用时的静强度、疲劳强度和疲劳寿命要求。

3）钩环中置的弹簧相较于钩环偏置的弹簧所受应力更小、更均匀，能有效提高其强度安全系数和延长使用寿命，所以在安装位置允许的条件下，应尽量使用钩环中置的弹簧。