基于无标度网络的信用风险传导模型
2022-11-11黄小莉冯婉琪吴蕾蕾
黄小莉,冯婉琪,吴蕾蕾
(1.西华大学电气与电子信息学院,四川 成都 610039;2.弗里堡大学物理系,瑞士 弗里堡 1700)
随着经济建设进程的不断深入推动,经济的稳定增长成为我国经济社会发展的重要目标。风险贯穿了金融工作业务往来的始终,如何利用技术创新更好防范风险是金融学者研究的重点,更是金融科技未来发展的趋势。在防范金融风险方面,倪琦瑄[1]采用图卷积算法聚合邻居节点的属性和连接信息,将复杂网络的拓扑结构投影到低维向量空间,有效挖掘和保存了信贷用户网络的深层信息,提高了信贷风险预测准确性。陈君[2]通过弱化信息不对称性和完善评估工具来完善信用评估体系,应用大数据进行信贷风险管理,建立了扁平化风险管理体系。李兆辉[3]利用神经网络算法建立了评判决策的信贷风险量化分级模型,做出了信誉等级图,可直观读出各企业信用等级。
由于现代金融体系具有高度市场化和风险分散性的特征,传导性风险在企业之间传播速度、强度以及范围都不断扩大加强。Allen 等[4]利用规则网络进行仿真,得出完全结构的银行间债务网络受到流动性冲击时更有稳定性的结论,对于债务网络与风险传染的研究具有开创性的意义。Thurner 等[5]利用星形网络、随机网络、全连接网络模拟债务传染的过程。Gai 等[6]通过模拟随机网络上银行债务传递,发现银行破产数量随着连接数量增加而减少。然而,随着研究的深入,学者们发现包含银行间债务网络在内的企业间业务网络并不是规则网络或随机网络。Upper 等[7]和Craig 等[8]研究发现,在银行间债务网络中规模较小的银行往往不会借钱给其他小银行,而是更倾向于与其他规模大、信誉好的银行进行往来。Boss 等[9]分析奥地利债务市场后也发现节点度服从幂律分布,即具有无标度特征。隋聪等[10]分析了中国银行间数据,得出中国同业网络具有无标度特性的结论。
在从复杂性研究的新视角探究传导模型方面,Zhang 等[11]提出了一种考虑超级传播机制的谣言和权威信息传播模型,并将BA 无标度网络[12-13]上的仿真结果与实际微博数据进行比较验证。Zhu 等[14]结合时间与空间 2 种维度来探究谣言传播的过程。Huang 等[15]深入研究了一类具有弱保护和强保护敏感节点的新型网络传染病模型。Ma 等[16]提出了一种新方法,实现精准识别单时延、多时延和分布式时延,并在实验中揭示了空气污染物作为疾病的原因。
由以上关于传导性风险以及传导模型的分析可知,在对信用风险的传导研究时可从复杂性的视角切入。复杂网络不仅研究各类网络的静态结构,还可以分析网络的动力学特性,适用于分析谣言、舆论、疾病等的传播过程。因此,本文从复杂网络的动力学系统出发,提出一种基于无标度网络的信用风险传导动力学模型——NCAR(normal-credit risk occurred-affected-recovered from credit risk)模型。该模型更注重信用风险的内在传导机制,并且考虑了各类干预措施对于模型的影响以及底层网络的无标度特性,同时也考虑了由于风险冲击导致企业破产和新企业成立的问题,这些都使得模型更符合实际情况。
1 信用风险传导分析
1.1 企业间网络结构分析
在企业构成的链接网络中,将企业个体抽象为节点,企业之间的业务往来抽象为连边。假定该网络中有n家企业,在不考虑企业间业务往来的权重大小,只考虑是否存在业务的情况下,企业间的业务往来网络可以用n阶的邻接矩阵来表示。
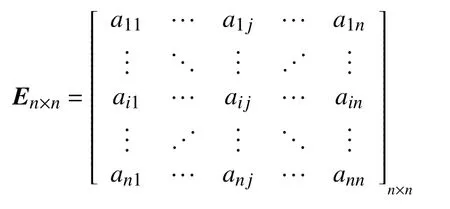
式中:ai j=1表示企业i与企业j之间存在业务往来;ai j=0表示企业i与企业j之间不存在业务往来。
网络中企业的同质性是指企业个体之间高度无差异,不论是规模、声誉、资产流动性等都相同。这种假设会更注重从宏观角度讨论市场发展规律,对于企业个体的作用考虑不足,并且在现实社会中也不可能存在有这样的企业,因此,本文风险传导模型的研究是基于企业具有异质性的。具有异质性的企业更倾向于与规模更大、声誉更好、资产流动性更高的企业进行合作,这一点恰好符合无标度网络中节点更倾向于链接度值较大节点的特征。无标度网络由于节点个体异质性,使得节点之间连线数量的分布状况存在差异,网络中大部分节点只拥有少量连线,少量节点拥有大部分连线。本文提出的动力学模型就是基于无标度网络的,网络度分布满足幂律分布。
1.2 经典传染病模型
传染病模型即是传染病的基本数学模型。根据传染病的各项参数建立的合理模型,可以更好研究传染病的传播速度、范围以及内在传播机制等,对于防治传染病,管控其扩散传播有着十分重要的意义。经典传染病模型有SIS 模型[17]、SIR 模型[18]等。这2 类模型将人群分为了几类:S(susceptible)类易感者、I(infected)类感染者和R(recovered)类恢复者。S 类指还未被感染疾病但有感染可能的人群;I 类指已经感染疾病且有传播能力的人群;R 类指已感染疾病但恢复了健康并且有免疫能力的人群。
传染病模型虽然最开始提出是为了刻画传染病在整个传播过程中的扩散机制,但是现在已经广泛用于舆情传播、谣言演化、信息传播等行业[19-21],尤其是金融风险领域。从较为微观的层面分析看,当金融风险在企业之间传播的时候,其环境、对象和传播机制都很类似于传染病传播。文献[22 -24]指出金融风险的传播非常类似疾病传播。传染病模型因在刻画金融风险扩散传导方面的优势而不断被扩展和创新,出现了SIRS模型、SEIR 模型等[25]。
1.3 NCAR 模型的建立
在发生系统性风险前,相关监管部门可以允许信用风险在各个经济个体之间传播扩散,财务状况良好的企业能够顺利度过危机,而财务状况本就存在问题的企业则会濒临破产,这一机制使得经济个体在市场作用下自发进行优胜劣汰。然而相关监管部门的“不干预”政策也会在一定程度上导致社会经济的剧烈波动,因此,面对较大范围的风险蔓延和可能会发展成为系统性风险的情况,监管部门还是会采取一定的措施来进行市场干预。
典型的风险干预手段有2 种。一种是当某企业受到信用风险的传导时,其他企业积极提供帮助,那么该企业的违约概率就会大大降低甚至不会产生违约行为,不会对网络中的其他企业产生影响,该策略被称为“救援策略”。第二种是受到信用风险传导的企业主动切断与其他企业的业务往来联系,通过改善资本结构等措施来增强自身抵御风险传染的能力,该策略被称为“免疫策略”。
基于以上2 种策略,本文提出了NCAR 模型,流程图如图1 所示。
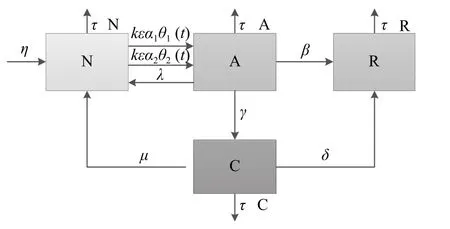
图1 NCAR 模型流程图
该信用风险传导模型由4 类节点组成,分别为:
1)尚未发生信用风险的正常企业N(normal),该类企业自身财务状况良好,但容易受到其他企业的信用风险传导;
2)自身陷入信用风险危机的企业C(credit risk occurred),该类企业财务状况较差,已经发生信用风险,且具备传导风险的能力;
3)被传导信用风险的企业A(affected),该类企业资本结构脆弱,抗风险能力较差,已被其他企业传导信用风险;
4)已从信用风险中恢复的企业R(recovered from credit risk),该类企业经过各项干预手段,已经脱离了此次系统性风险。
信用风险传导过程为:N 类企业因C 类企业的传导以概率α1转变为A 类企业,因A 类企业的传导以概率α2转变为A 类企业;A 类企业若也因自身原因陷入了信用风险,则以概率γ转变为C 类企业;因为“救援策略”的干预,A 类企业和C 类企业分别以概率λ和μ转化为N 类企业;因为“免疫策略”的干预,A 类企业和C 类企业则分别以β和δ的概率转变为R 类企业。其中,ε表示N 类企业抵抗信用风险的能力,能力越低越容易被传导风险,而θ1和θ2则分别表示了N 类企业受到C 类和A 类企业传导的概率。模型中还考虑了新企业成立加入经济网络以及现有企业破产退出经济网络的情况,用概率η表示新企业的迁入率,用概率τ表示现有企业的迁出率。
令Nk(t)、Ck(t)、Ak(t)和Rk(t)分别表示t时刻在度值为k(k=1,2,3,···,n)的节点中各类企业的相对比例。根据平均场理论,可以得到NCAR 动力学方程,为:
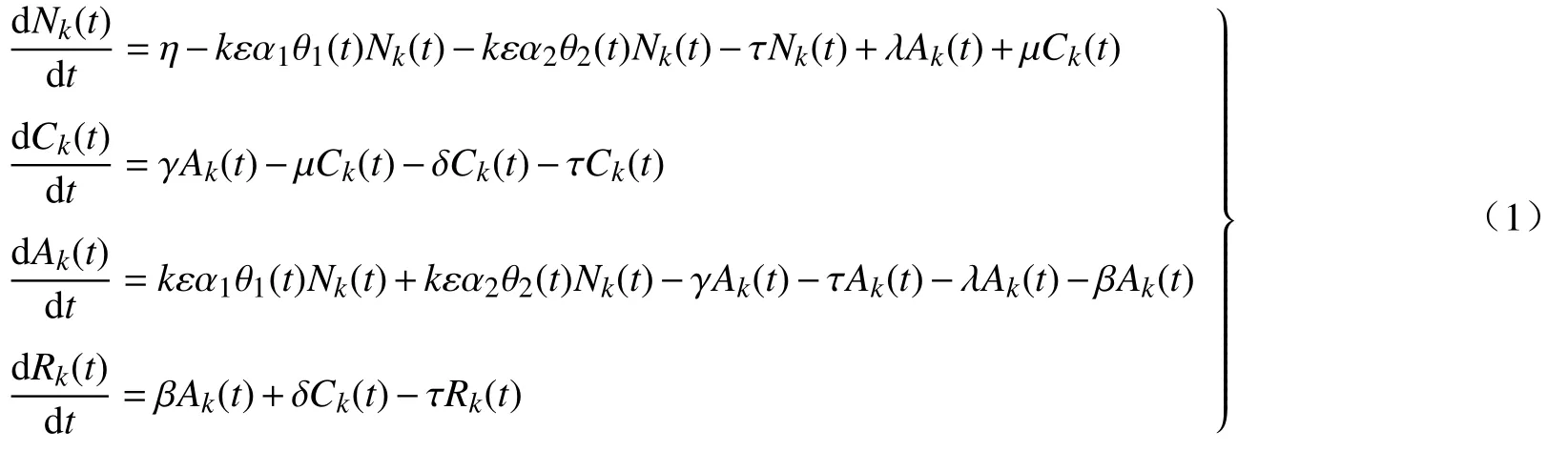
式中:θ1(t)代表在t时刻N 类企业与C 类企业之间存在信用风险传导的概率,满足
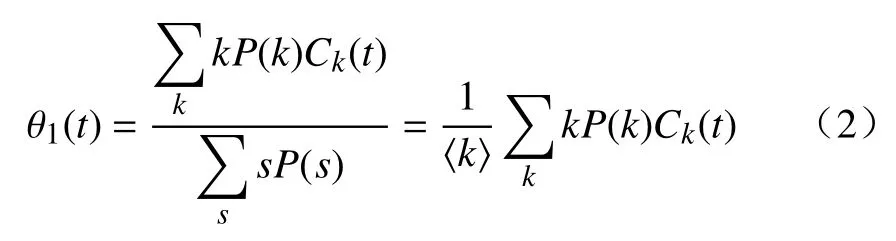
θ2(t)代表在t时刻N 类企业与A 类企业之间存在信用风险传导的概率,满足

因此,在t时刻,总站点数满足
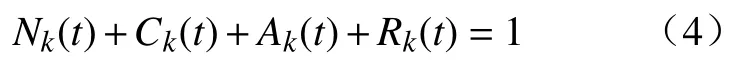
在t=0 初始时刻,4 种站点的比例应该满足:
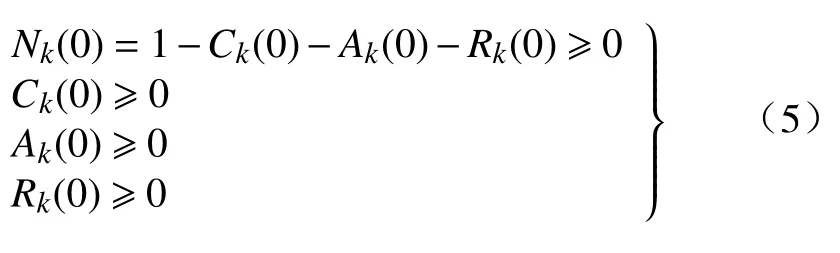
2 模型的平衡点分析
在传染病模型中,基本再生数(basic reproductive rate)指一个病例在全部都是易感者的人群中直接造成的新感染者的平均人数。在本文NCAR 模型中,基本再生数指的就是一个陷入信用风险的企业在平均风险传导期内所能传播的企业数量。
令基本再生数为

则可以得到:
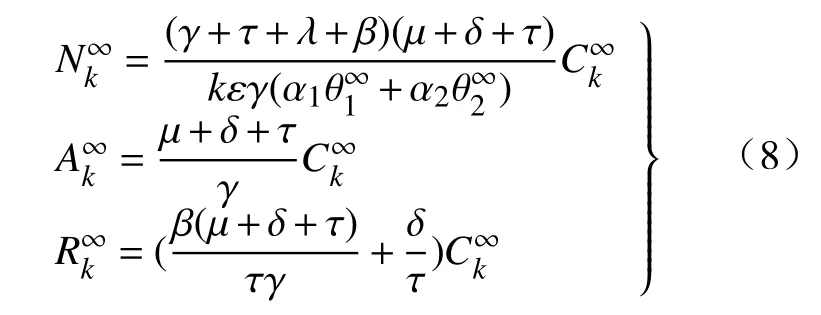
根据式(2)和式(3),可以计算出
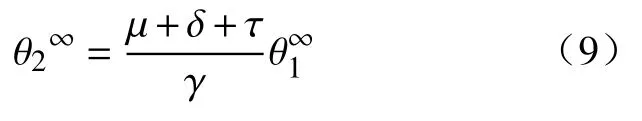
根据Nk(t)+Ck(t)+Ak(t)+Rk(t)=1,可得到
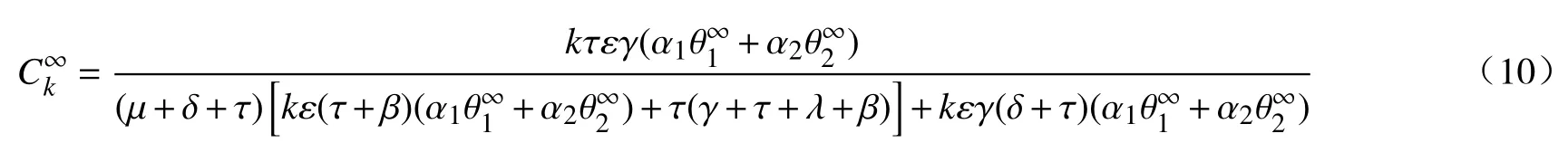
将方程式(10)代入式(2),可得到
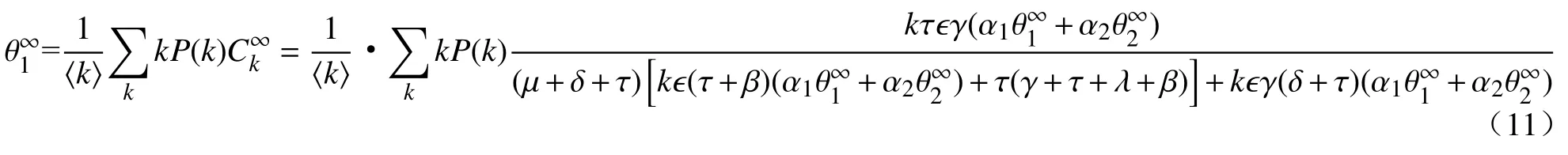
再将式(9)代入式(11),可得
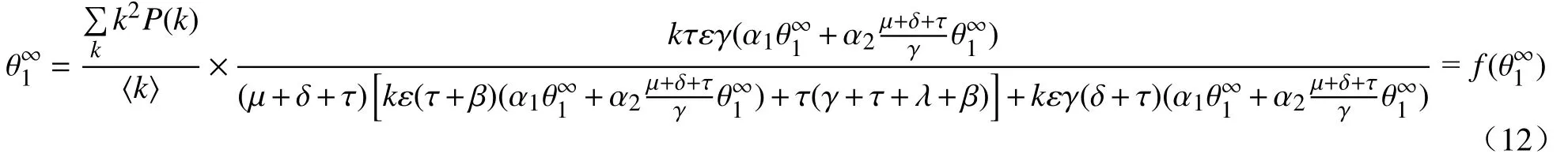
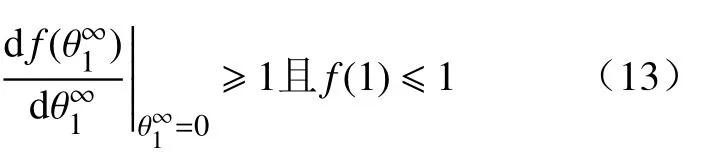
综上所述,可以得到该系统中的阈值,即基本再生数为
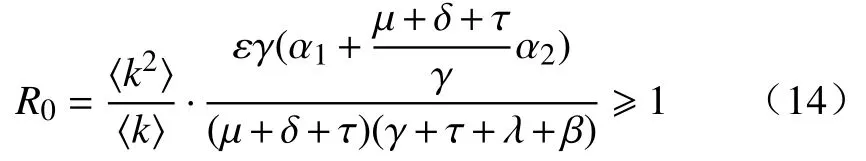
由此可知,当且仅当R0≥1 时,方程存在非平凡解。将非平凡解代入方程式(10),可得到,由方程式(8)得到:

由证明过程可知,系统的基本再生数R0受复杂网络的拓扑结构影响,即复杂网络关于平均度的参数〈k2〉/〈k〉越大,系统的基本再生数越大,即信用风险越容易在企业之间进行传导。通过更改参数大小可以控制企业间信用风险的传导范围,这为制定措施控制风险,加强信用体系建设提供了新的解决思路。
3 信用风险传导仿真结果
3.1 模拟风险传导效应的结果
模型的仿真实验均基于MATLAB 平台。仿真实验中,设置各类企业的初始状态分别为:Nk(0)=0.4,Ck(0)=0.3,Ak(0)=0.3,Rk(0)=0。并且设定NCAR模型处于无标度网络中,规模的大小为站点数S=1 000,平均度值 〈k〉=4,其度分布满足P(k)=2m2k-3。
下列参数的设定均经过多次实验调整,使各类企业比例变化曲线离散程度最大,仿真结果最好。
3.1.1 无干预手段下的仿真结果
在不采取措施干预风险传导的情况中,选取参 数α1=0.8,α2=0.6,γ=0.2,β=0.1,δ=0.1,ε=0.1,λ=0.1,η=0.1,τ=0.1,μ=0.1,仿真结果如图2 所示。
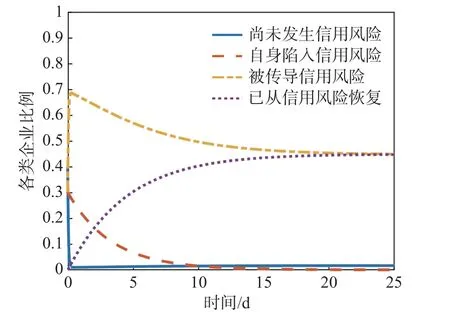
图2 无干预手段下信用风险传导过程
由图2 可知,在没有外力干预下,信用风险开始在企业之间传导。尚未发生信用风险的企业在传播开始后比例骤降,而被传导信用的企业比例则迎来了激增。自身陷入信用风险的企业通过改善自身资产结构逐渐恢复了正常,比例逐渐减少。信用风险在前10 d 内迅速在企业之间传播,比例最终在第20 d 达到稳定。这表明从第20 d 起,整个网络中的风险传导达到了一个稳定的状态,此时基本再生数为
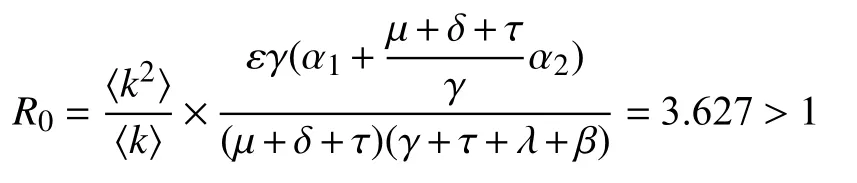
经济网络达到了信用风险持续传导的平衡点,仿真结果与模型结论一致。
由图1 可知,影响信用风险向外传导的参数一共可分为2 类。1)由于救援策略的干预,企业间信用风险降低,但该类策略的实行取决于其他企业的救助,因此,被救援后的企业仍有可能被传导新的风险,在这里就将救援策略抽象为了A、C 类企业转化为N 类的概率λ和μ;2)免疫策略则是企业调整自身结构,提升抗风险能力从而避免信用风险传导,因此A、C 类企业由概率β和δ转化为R 类企业。下面就分别模拟这2 类策略干预下的信用风险传导过程。
3.1.2 模拟救援策略干预下的风险传导仿真结果
将救援策略的2 个参数分别设定为几个不同值,保持其他参数不变的情况下,观察被传导信用风险的企业比例变化。仿真结果如图3 所示。
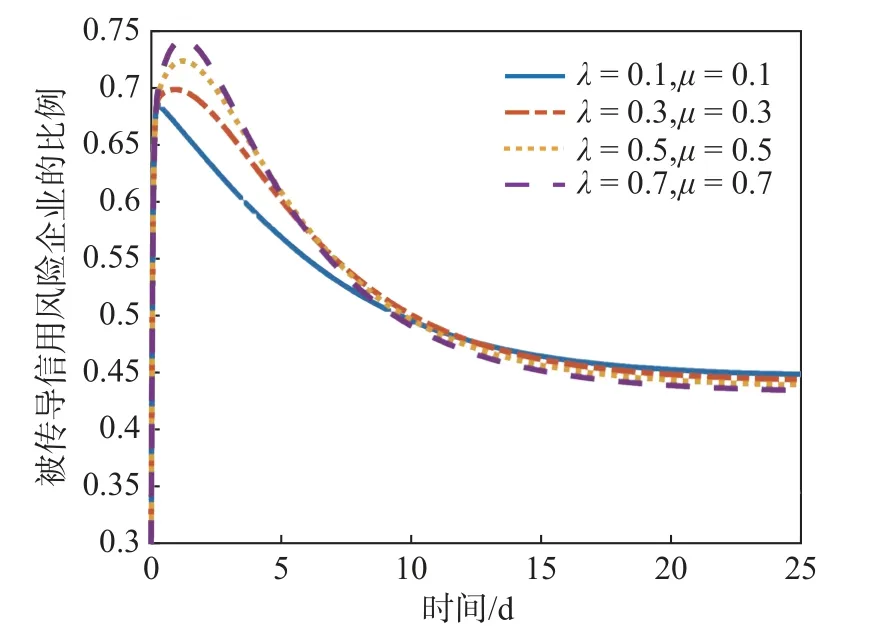
图3 救援策略干预下信用风险传导过程
由图3 可知,当几乎不采取措施(λ=0.1,μ=0.1)时,被传导信用风险的企业在第20 d 时比例稳定在45.3%,而当相关部门采取一定救援措施后,受传导企业的比例就会下降,即信用风险对经济造成的损害也随之降低,λ和μ值越大,受传导企业的最终比例就越小。该结果表明,监管部门的救援策略会较为有效地降低企业受到信用风险波及的可能,同时,如果投入的救援成本越高,甚至可能直接达到无风险的稳定状态,使整体经济快速平稳发展。
3.1.3 模拟免疫策略干预下的风险传导仿真结果
将免疫策略的2 个参数分别设定为几个值,保持其他参数不变的情况下,观察被传导信用风险的企业比例变化。仿真结果如图4 所示。
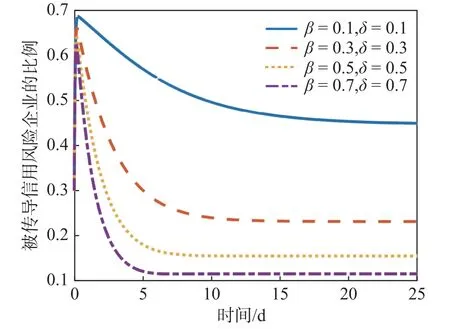
图4 免疫策略干预下信用风险传导过程
由图4 可知,在不采取免疫措施(β=0.1,δ=0.1)的情况下,被传导风险的企业比例在第23 d 时达到45%,而当监管部门采取免疫策略后,受传导风险企业的比例显著下降。如β=0.3,δ=0.3 时,在第10 d 就下降到了23%;当β=0.5,δ=0.5 时,在第9 d达到了15.6%;当β=0.7,δ=0.7 时,比例迅速下降,在第7 d 就降至11.6%。这表明,免疫措施力度越大,就可以越早遏制住风险的扩散。可见,当发生危险事件时,免疫策略比救援策略更为迅速有效,这为以后各项方案的制定提供了参考。
3.2 信用风险传导模型的灵敏度分析
3.2.1 改变α1和α2的值
设定参数:γ=0.02,ε=0.1,λ=0.5,η=0.1,τ=0.1,μ=0.2,β=0.2,δ=0.5。逐渐增大α1和α2的值,观察被传导信用风险企业的比例变化情况。仿真结果如图5 所示。
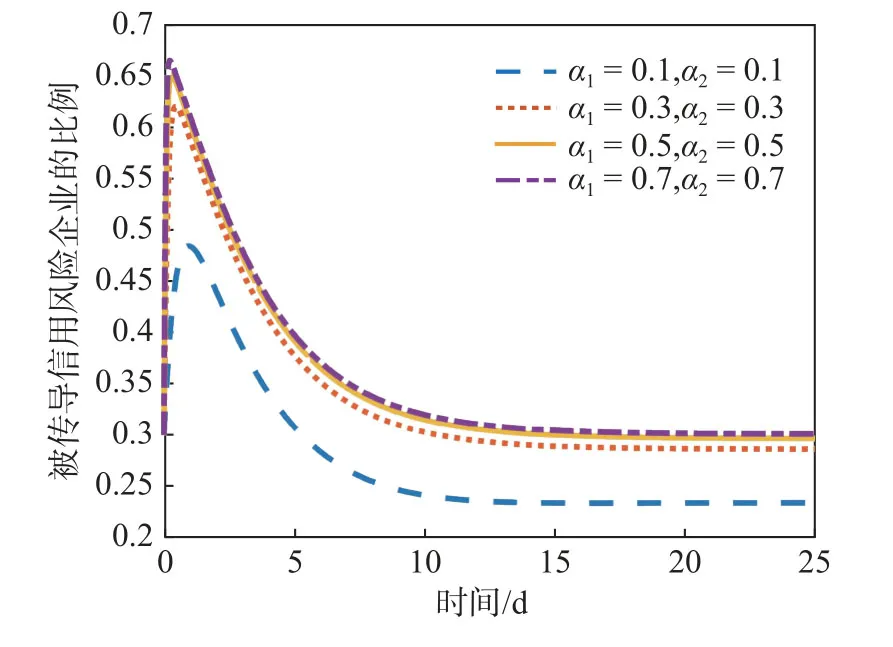
图5 NCAR 模型对于α1 和α2 的灵敏度
由图5 可知,被传导风险的企业的比例会在开始传导过程后迅速提高,在达到峰值后随着时间缓慢下降。随着α1和α2的逐渐增大,被传导信用风险的企业的最终比例逐渐增高,此时的信用风险更具破坏性。当传导能力较弱时(α1=0.1,α2=0.1),比例的峰值最低,且最终稳定在0.24。当传导能力加强时,比例的峰值和最终值都会有较大的增长,但并不因为α1和α2的均匀变化而均衡改变。这代表整个传导过程的影响因素很多,α1和α2值的影响也是有限的。
3.2.2 改变γ的值
设定参数:α1=0.1,α2=0.1,ε=0.1,λ=0.5,η=0.1,τ=0.1,μ=0.2,β=0.2,δ=0.5。改变γ的值,观察被传导信用风险的企业比例的变化。仿真结果如图6所示。
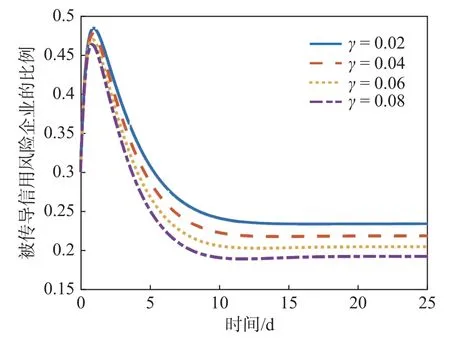
图6 NCAR 模型对于γ 的灵敏度
由图6 可知,当风险开始传导后,被传导风险企业的数量先会在第1 d 迎来快速增长,达到峰值后,数量逐渐减少,到第10 d 左右稳定在最终值。原因可能是企业通过自身的抵抗能力和各类干预措施恢复了正常业务往来摆脱了风险转变为R 类企业,也有可能是因为企业自身陷入无法履行合同的危机转变为了C 类企业。从图中还可以看出,γ值越大,被传导企业风险的数量下降得更快,且最终比例也最低,此时被传导风险的企业更多地转化为了C 类企业,即网络中有了更多的风险传导源头,这时的经济面临着更大危机。
3.2.3 改变各类企业的初始值大小
设定参数:α1=0.1,α2=0.1,γ=0.02,ε=0.1,λ=0.5,η=0.1,τ=0.1,μ=0.2,β=0.2,δ=0.5。改变各类企业初始值大小,观察被传导风险企业的比例变化。仿真结果如图7 所示。
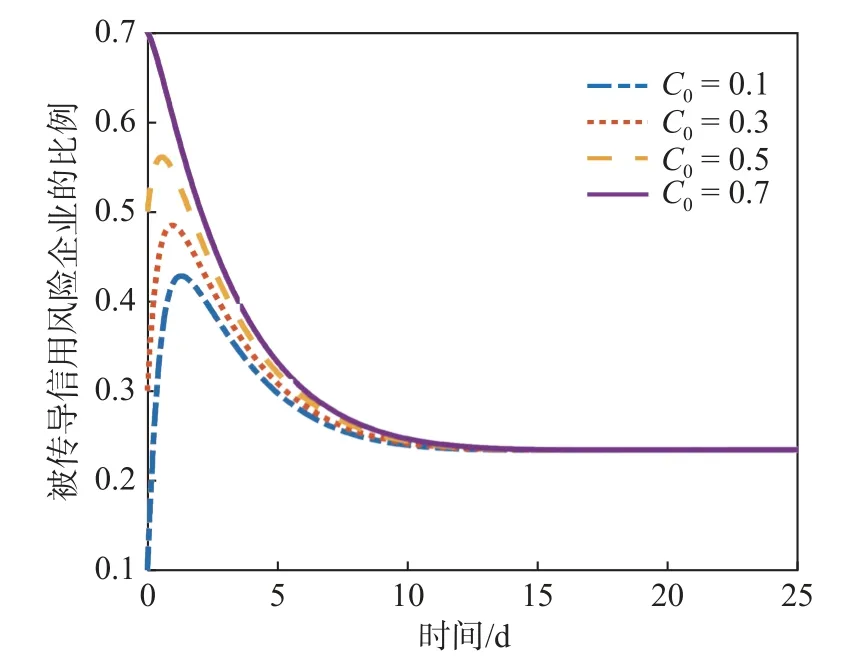
图7 NCAR 模型对于初始值大小的灵敏度
由图7 可知:当C 类企业的初始值为0.1、0.3和0.5 时,被传导风险企业的数量先迎来迅速增加,在第2 d 达到峰值后缓慢下降;当C 类企业的初始值为0.7 时,被传导风险企业的数量会持续下降。无论初始值大小为多少,C 类企业的比例都会在第13 d 左右稳定在同一个值。这证明了初始值大小并不影响模型的演化过程,即风险开始传导时,无论各类企业最开始数量为多少,只要企业抵抗风险能力和各类参与措施力度不变,最终达到稳定时的企业数量也保持不变。出现这种结果的原因是:观察基本再生数的计算公式,其中不包含初始值大小,因此不管初始值如何改变,都不能加快或延迟模型的演化。这一点对于控制风险传导的时间和范围有一定借鉴意义。
3.2.4 改变度值的大小
设定参数:α1=0.1,α2=0.1,γ=0.02,ε=0.1,λ=0.5,η=0.1,τ=0.1,μ=0.2,β=0.2,δ=0.5。改变度值大小,观察被传导风险企业的比例变化。仿真结果如图8所示。
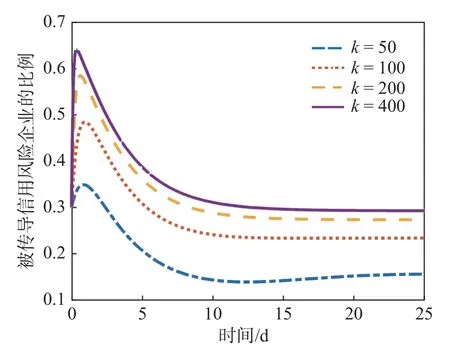
图8 NCAR 模型对于度值大小的灵敏度
由图8 可知,当度值增加时,即网络模型内部关联结构更复杂时,被传导信用风险企业的比例峰值和稳定值更高。当度值为50 时,企业比例最终稳定在0.16 左右;当度值为100 时,企业比例最终稳定在0.24 左右;当度值为200 时,企业比例最终稳定在0.28 左右;为当度值为400 时,企业比例最终稳定在0.29 左右。这说明当一个企业度值越大,与其余企业的业务往来越频繁,越容易受到信用风险的传导。因此当已有企业陷入危机时,积极采取手段加强自身抵抗风险能力,尽快暂停与危机企业的业务合作非常重要。
4 结束语
本文根据平均场理论列出了信用风险传导模型的动态方程,在计算出方程的基本再生数和平衡点后进行了仿真实验。通过理论推导和仿真实验可以得出,信用风险会在无标度网络的传导过程中逐渐收敛到稳定状态。决定风险的稳定状态是消失还是持续存在,就在于基本再生数的大小。当基本再生数大于等于1 时,信用风险将会持续影响经济网络,系统将会收敛至有风险的稳定状态;当基本再生数小于1 时,市场会自发修复信用风险冲击造成的失衡达到无风险稳定状态。风险稳定水平所对应的被传导企业比例,与表征救援策略的λ和μ呈负相关,与表征免疫策略的β和δ呈负相关,与表征传导概率的α1和α2呈正相关,与转化为自身陷入风险概率的γ呈负相关,与度值k呈正相关,与初始值大小无关。在多数情况下,监管部门的政策干预是必要的。如果任由危机蔓延,很可能引发整个体系的金融风险,在一定措施的干预下,危机蔓延的过程可以减缓甚至逆转。从干预效果来看,免疫策略优于救援策略。
