大峰露天矿边坡稳定性分析与治理措施研究

侯 敏

(国家能源集团 宁夏煤业有限责任公司，宁夏 银川 750000)

根据统计数据显示，露天矿山数量较多，特别是铁矿和有色金属矿就约有1 500个，其中大型矿山数量分别达到40个和12个。截至2017年，全国建材类矿山露天开采量占100%，冶金辅助材料露天开采量占总开采量90.5%，铁矿石露天开采量占总开采量86.4%，有色金属矿露天开采量占总开采量49.6%，煤炭露天开采占总开采量5%。露天开采由于安全条件好、机械化程度高、资源回收利用率高等优点，成为浅埋矿床首选方法[1-5]。

由于露天开采优越的交通环境，为了进一步提高矿山开采效率，越来越多先进高效的钻孔设备得到应用，大孔径、高台阶爆破技术得到发展，特别是在矿岩硬度比较大的露天矿φ310 mm牙轮钻机逐步取代了φ200、φ250 mm潜孔钻机，露天矿开采出矿量越来越大，年开采深度越来越深，矿山开采效率逐步增大的同时，边坡安全隐患也越来越多。

20世纪50年代，我国边坡稳定性研究开始起步，主要以材料力学和简单的土力学进行边坡稳定性计算。60年代，边坡研究理论得以发展，其中以岩体结构理论和流变理论为代表。70年代，结合矿山实际情况，建立了相应的过程地质模型，开展了工程地质力学研究[6]。80年代开始推广应用数值模拟技术及边坡可靠性分析，经过近70年的发展，边坡稳定性研究理论不断成熟，将传统的方法不断发展，结合新的理论和试验，逐步形成了定性和定量分析法[7-11]。大峰矿煤层具有“太西无烟煤”称号，品味高，含有杂质较少，工业生产过程中，燃烧值高，污染较少，在冶金和化工等方面得到广泛的应用。1958—1996年为露天小规模开采，1996—2006年为井工开采，由于地采受火区影响停止生产，2011年开采呈规模露天开采，由于大峰矿煤层较多，赋存条件复杂，随着开采深度不断加大，边坡失稳现象逐步增多。因此本文通过对大峰露天煤矿进行详细的现场勘查及资料收集整理，利用已知的矿岩性质，运用相关理论进行边坡安全系数计算，并采用FLAC3D分析软件建立特征边坡模型，分析不同结构参数下边坡终了状态的位移、应力分布特征等，对大峰露天煤矿终了边坡的稳定性进行深入系统的研究，提出边坡防护措施并应用于现场实践。

1 工程概况

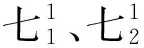
2 边坡稳定性系数理论计算分析

边坡的安全系数是边坡稳定性的最重要的衡量指标，根据《岩土工程勘察规划》(GB 50021—2001)(2009年版)，边坡稳定性系数对于新设计的边坡：重要工程宜取1.3～1.5，一般工程宜取1.15～1.30，次要工程宜取1.0～1.15。本工程边坡稳定性安全系数允许值取k0=1.3。

2.1 非工作帮边坡系数理论计算分析

非工作帮边坡中含有2层软弱的煤层，煤层与相邻的岩体物理力学性质差别较大，近似于两条平行的层理，根据文献[12]顺层边坡的滑坡特点，层理面平行于砂岩岩层，且非工作帮终了边坡层理贯穿岩体，在层理作用下极可能发生顺层滑坡。

岩体结构面与边坡坡面的产状对于边坡稳定起着控制作用，大峰矿顺层边坡滑动受力分析如图1所示。

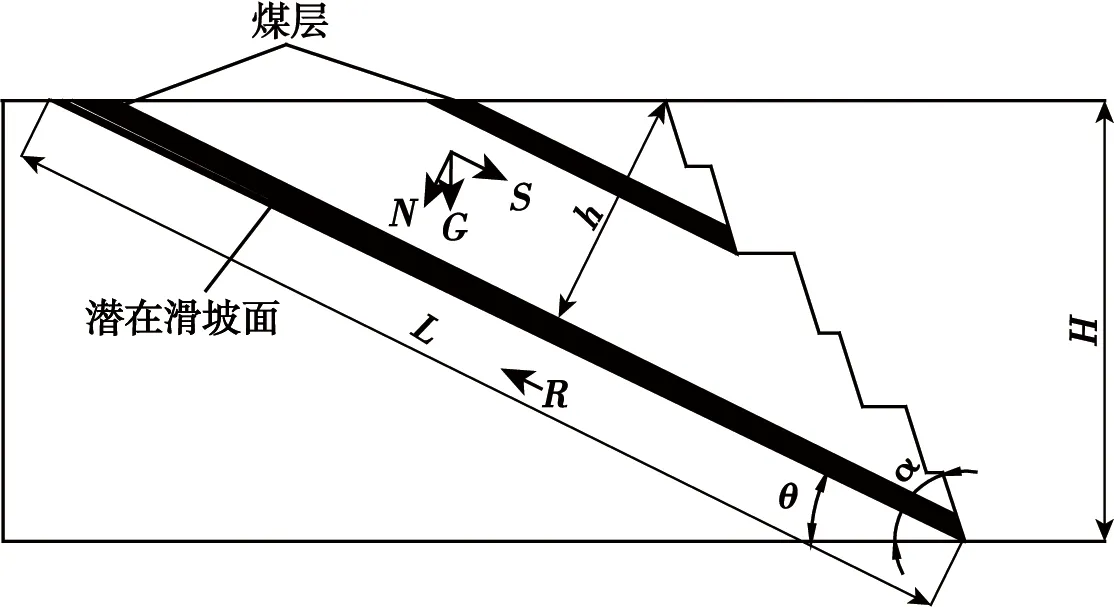
图1 大峰矿顺层边坡滑动受力分析Fig.1 Stress analysis diagram of slope slide of Dafeng open pit mine

边坡稳定性系数k可以由抗滑力R与下滑力S之比表示：

(1)

式中，c为岩体内聚力；θ为潜在滑面倾角；φ为岩体内摩擦角；L为潜在滑面长度；α为开挖坡角；G为岩体自重；γ为岩体的容重；H为边坡高度；h为边坡切层高度。

(2)

将式(2)代入式(1)，整理得：

(3)

大峰露天煤矿开采过程中，若忽略人为因素，由式(3)可知，非工作帮边坡不同结构参数安全系数分析可得：影响安全系数的可变参数为台阶高度和坡面角，并且安全系数随着台阶高度增大而降低，随着坡面角的增大而降低。

2.2 端帮边坡系数理论计算分析

大峰矿终了边坡端帮层理面呈水平分布，与砂岩岩层的夹角较大，根据文献[13-15]对圆弧滑动的判断，确定端帮的可能滑坡属于圆弧滑坡。采用圆弧形条分法对圆弧滑坡的土坡稳定性进行分析，这种方法认为边坡岩体的滑动属于平面问题，并假定滑面为圆弧形，其位置和安全系数要通过反复试算确定，计算中不考虑条块间的作用力。计算模型如图2所示。

图2 圆弧形滑动计算模型Fig.2 Calculation model of circle failure

计算在每一条块上的力，将每一条块的自重分解为垂直于滑动面的法向压力Ni和平行于滑动面的切向力Ti，即：

Ni=Wicosαi

(4)

Ti=Wisinαi

(5)

式中，φ为岩体的内摩擦角；αi为通过条块重心的垂线与底边线的夹角；C为条块滑面上的内聚力。

作用在该条块所对应的长为Li，滑面上尚有摩擦力Nitanφ与总内聚力CLi，此二力是抵抗滑动的抗滑力。

在条块界面上还有垂直于平行条块界面的E1，E2，T1和T2等作用力，为简化计算，假定T1=T2，E1=E2，故在计算中这些力不予考虑。

计算各条块的下滑力对圆弧圆形O点的力矩M1：

(6)

计算各条块抗滑力对O点的力矩M2：

(7)

则安全系数n为：

(8)

式(8)为端帮终了边坡安全系数计算理论，由于公式较复杂，无法直接算出安全系数，因此采用数值模拟进行分析和计算。

3 边坡稳定性数值模拟分析

3.1 岩体物理力学参数

三维模型计算时需要赋予矿岩物理力学性质，包括体积模量K和剪切模量G，通过以下公式进行计算：

(9)

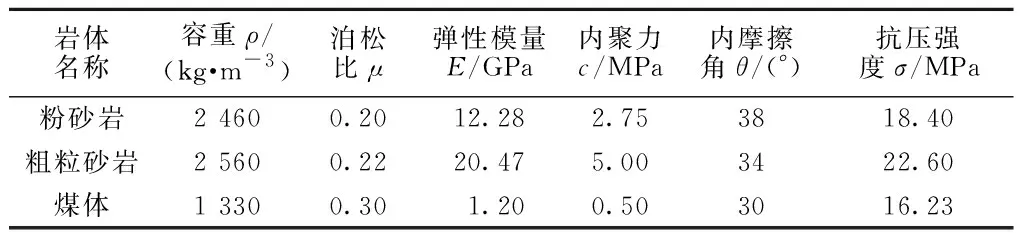
表1 岩层物理力学参数Tab.1 Physical and mechanical parameters of rock formations

(10)

3.2 三维数值模型

由第1节分析可知，根据大峰露天开采根据岩层产状及边坡特征，终了边坡主要存在2种破坏模型：①非工作帮边坡破坏模型；②端帮边坡破坏模型，在有限元软件Midas-Gts上建立了大峰露天煤矿2种终了边坡工程地质三维仿真模型。

非工作帮边坡高度约96 m，边坡无大型结构断裂，但是存在2个煤层，2煤层夹在边坡中，且煤层倾向与最终边坡的倾向大致平行，煤层厚度取3 m，如图3所示。由于煤的物理力学性质与周边岩石的物理力学性质差别较大，煤层在边坡中类似于层理面，对边坡的破坏形态起决定性作用。三维建模时岩体网格划分越小，计算结果越精确，因此，本模型三维尺寸为，x∈(0，10)，y∈(0，100)，z∈(0，96)，共建立15 214个节点，27 912个单元。本次模型以横剖面Ⅷ剖面为基础，上层岩体结构为粉砂岩，下层岩体为粗粒砂岩。

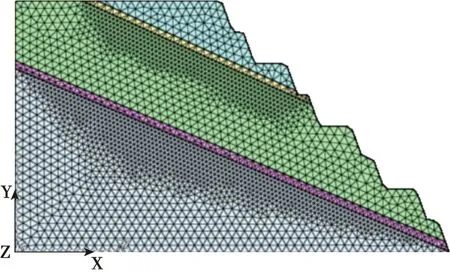
图3 非工作帮边坡计算模型Fig.3 Calculation model of non-work wall slope

端帮边坡高150 m，边坡内部无大型的结构断裂，存在3层煤层与水平面大致平行，岩体上部为粉砂岩，下部为粗粒砂岩，如图4所示。煤层厚度取3 m，模型以矿山纵剖面9剖面为基础，共有 184 292个节点，35 464个单元。边坡在3个坐标轴上的位置分别为：X∈(0，130)，Y∈(0，100)，Z∈(0，150)。

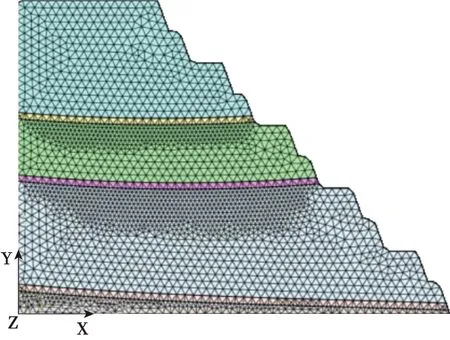
图4 端帮边坡计算模型Fig.4 Calculation model of slope

3.3 边坡稳定性数值结果

基于第3.2节有限元软件Midas-Gts对两种边坡建立数值模型的基础上，再将模型导入FLAC3D三维软件进行计算并分析边坡应力特点。根据其应力分布判断边坡潜在的破坏特征，分析结果如下。

(1)非工作帮边坡。模型中有2个煤层，即2个断裂面，经过数值计算后，由图可以看出，在第1层煤层应力符合自重应力分布特征，无应力集中点，但是在第2层煤附近出现了应力的集中，主要体现为应力在岩滑动面较周边岩体应力明显的突变，说明终了边坡的滑面出现在第2条层理面。

由图5—图8对X、Y、Z三个方向应力进行分析后发现，非工作帮终了边坡由于存在2层倾斜的层理(煤层)，层理结构上覆岩层沿着层理面存在较大的下滑力，且第2层层理结构下滑力明显大于第1层层理面，第2层层理埋藏大于第1层层理面，说明在第2次层理面上，自重应力在层理面上的分力大于层理面的摩擦力，终了坡面下滑力明显增大，非工作帮终了边坡出现顺层滑坡破坏特征。

图5 X方向应力云图Fig.5 Stress nephogram of X-direction

图6 Y方向应力云图Fig.6 Stress nephogram of Y-direction

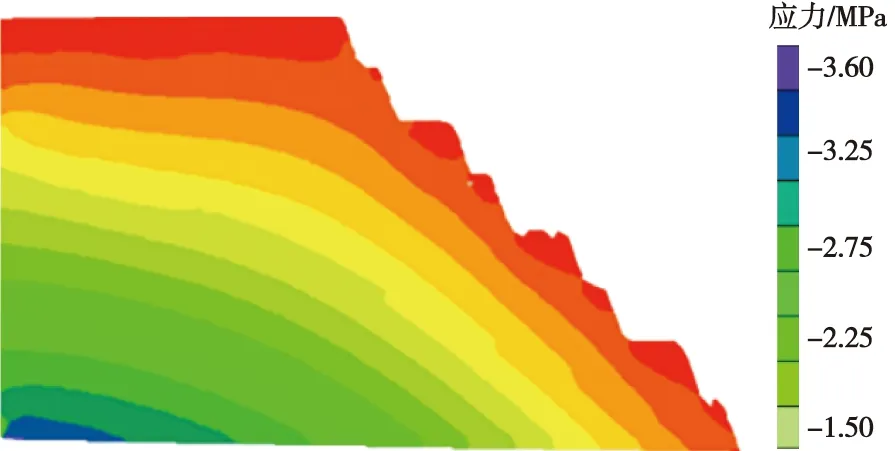
图7 Z方向应力云图Fig.7 Stress nephogram of Z-direction

图8 最大主应力云图Fig.8 Nephogram of maximum principal stress

(2)端帮边坡。由图9—图12对端帮进行数值模拟分析发现，其破坏模式较非工作帮有较大的区别。端帮的节理断层更多，但是由于其节理与水平面平行，与坡面近乎垂直，因此层理面对于坡面的影响较小。但是通过应力云图发现，X与Y方向应力和位移在节理面均有明显的变化，Z方向应力呈现弧形变化，说明在自重应力作用，端帮边坡出现圆弧形破坏特征。

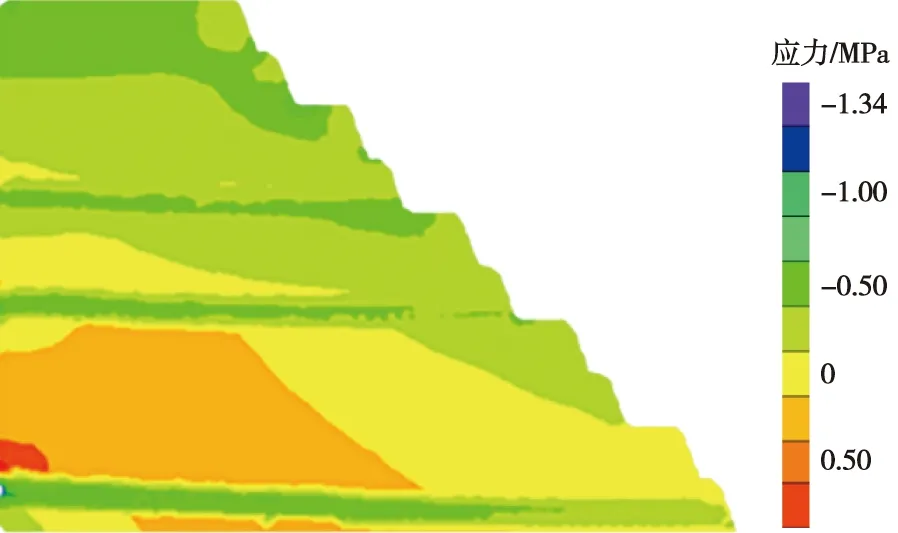
图9 X方向应力云图Fig.9 Stress nephogram of Y-direction

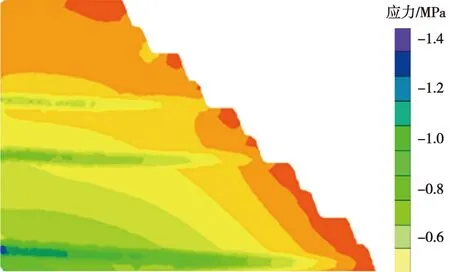
图10 Y方向应力云图Fig.10 Stress nephogram of Y-direction

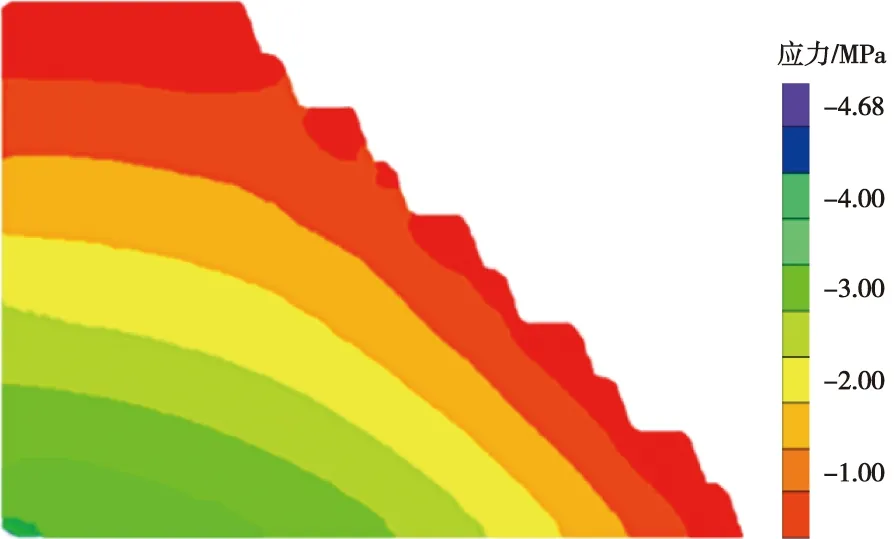
图11 Z方向应力云图Fig.11 Stress nephogram of Z-direction

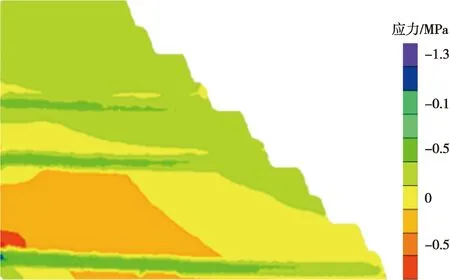
图12 最大主应力云图Fig.12 Nephogram of maximum principal stress

由上述数值结果分析可知，非工作帮边坡出现顺层滑坡破坏特征，端帮边坡出现圆弧形破坏特征，验证了第2节理论分析得出的2种边坡各自潜在的破坏形态。

4 边坡稳定性正交试验分析

由第2节与第3节分析可知，若不考虑其他人为因素的影响，影响矿山岩质边坡稳定性的主要因素为台阶高度、台阶坡面角、平台宽度，根据大峰矿初步设计建议，每个因素有一定的取值范围，不同取值对于终了边坡稳定性将造成较大影响。由于3个因素取值水平较多，采用常规的试验将进行3n次试验，试验次数繁多，效率低。因此，本次试验采用正交试验分析，正交试验分析就是选择其中一部分有代表性的水平组合进行试验分析，提高工作效率，减少工作量，3个因素三水平对于采用正交按L9(33)正交表(表3)，只需进行9次试验。

本次试验有3个因素，表示为A：台阶高度；B：台阶坡面角；C：平台宽度。试验方案见表2。

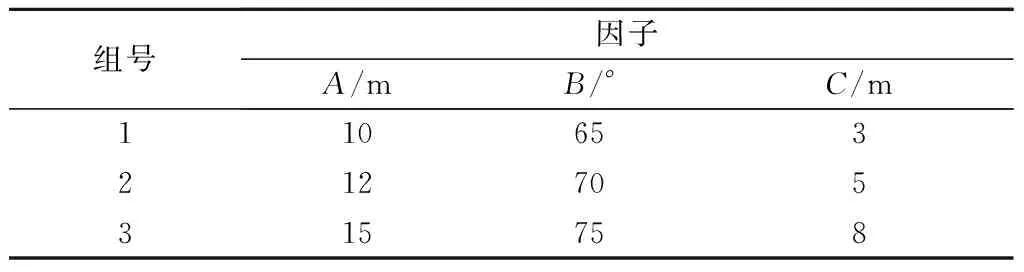
表2 边坡稳定性因素试验方案Tab.2 Slope stability factor test protocol

(1)安全系数计算方法。采用理论式(8)对圆弧性滑坡进行计算涉及参数众多，影响因素较多，在理论计算过程中计算繁琐且结果存在一定误差。FLAC3D能够用于边坡安全计算，且能够快速实现重复大量的计算。FLAC3D边坡的安全系数为滑面实际抗剪强度指标与发生破坏临界状态时虚拟的折减强度指标的比值，其计算原理为：

(11)

式中，K为安全系数；L为折减强度指标；φ为内摩擦角；c为岩体内聚力。

根据实际情况，逐步改变相关参数，得到不同的c′、φ′，代入FLAC3D反复迭代计算，直至坡体达到临界状态，坡体达到临界状态的K值即为边坡安全系数。利用莫尔—库伦强度准则，将边坡不收敛作为破坏标准，其表达式为：

(12)

式中，φ为内摩擦角；J2为应力偏量第二不变量；I2为应力张量第一不变量；c为岩体内聚力；θσ为应力罗德角。

按照表3所示方案采用FLAC3D分别对非工作帮与端帮终了边坡安全系数进行计算，运用正交试验分析表格进行统计分析，目标值为安全系数n。

(13)

R=max{K1，K2，K3}-min{k1，k2，k3}

(14)

式中，Ki为i列同一因子影响目标值之和；ki为i列目标值平均数；R为极差。

由表3(左列数据)可以明显看出3个因素的主次顺序依次B、A、C，即台阶坡面角对终了边坡稳定性影响最大，其次为台阶高度，最后为平盘宽度，因此影响非工作帮最主要的因素为台阶坡面角的设置，非工作帮为顺层边坡，坡面角越大，顺层坡上覆岩层压力越大，顺层滑坡几率越大。根据正交试验结果，边坡安全系数不小于1.3相对安全，安全系数越大，终了边坡剥离量越大，经济性越差，因此综合考虑安全因素和经济因素，非工作帮最优的边坡结构参数为A1B2C2，即台阶高度为10 m，台阶坡面角为70°，台阶平盘宽度为5 m时，效果最佳。

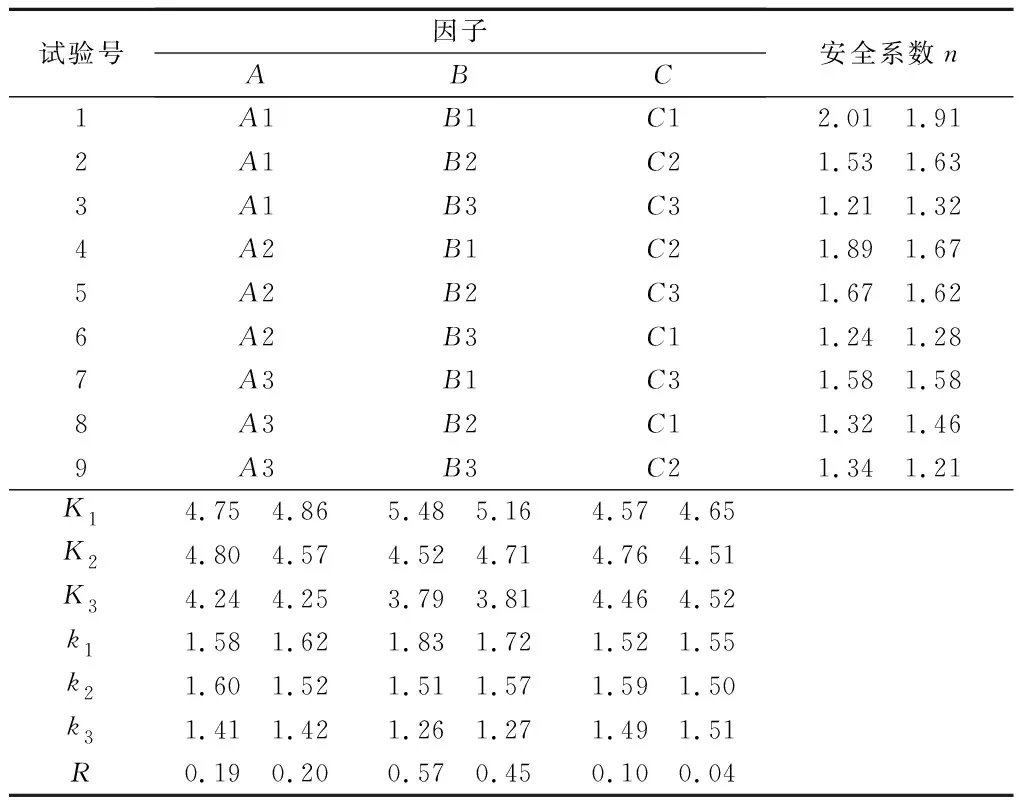
表3 非工作帮与端帮正交试验分析Tab.3 Orthogonal test analysis of non-working wall

从表3(右列数据)可以明显看出3个因素的主次顺序依次BAC，即台阶坡面角对终了边坡稳定性影响最大，其次为台阶高度，最后为平盘宽度，因此影响端帮最主要的因素为台阶坡面角，坡面角越大，其终了边坡角越陡，越不利于边坡的稳定，通过理论分析及数值模拟发现，端帮的破坏主要以圆弧形破坏为主，终了边坡角过大时，圆弧形破坏的趋势越明显。根据正交试验结果，边坡安全系数不小于1.3相对安全，安全系数越大，终了边坡剥离量越大，经济性越差，因此综合考虑安全因素和经济因素，端帮最优的边坡结构参数为A3B2C1，即台阶高度为15 m，台阶坡面角为70°，台阶平盘宽度为3 m时，效果最佳。

根据数值模拟的最佳结构参数，为减少大峰露天煤矿不同边坡产状滑坡的危害，大峰露天矿山非工作帮：台阶坡面角选择70°，台阶高度10 m，台阶平盘宽度为5 m；端帮边坡：坡面角选择70°，台阶高度15 m，台阶平盘宽度为3 m。数值模拟分析的优化方案应用于现场，同时通过工程经验采取一些其他优化措施，比如：排水过程、锚固技术与加强对边坡的监测等措施，最终大峰露天矿山未出现失稳现象，取得了较好的效果。

5 结论

(1)根据大峰矿边坡层理的分布特征，将边坡的潜在破形态分为2类：非工作帮为例的顺层滑坡与端面为例的圆弧形滑坡，通过理论分析得出影响2类边坡稳定性的主要因素有：台阶高度、台阶坡面角、平台宽度。并根据理论公式对2类破坏形态边坡的稳定性进行分析得出：安全系数随着台阶高度增大而降低，随着坡面角的增大而降低。

(2)采用FLAC3D分析软件对矿山边坡进行了三维建模数值仿真计算分析，对非工作帮与端帮边坡的应力、位移进行特征分析，验证了结论(1)2类边坡对应的破坏形态。

(3)运用正交实验分析法对边坡结构参数进行优化分析得出：非工作帮终了边坡台阶高度为10 m，台阶坡面角为70°，台阶平盘宽度为5 m时，安全系数为1.53；端帮最优的边坡结构参数为台阶高度为15 m，台阶坡面角为70°，台阶平盘宽度为3 m时，安全系数为1.46，均大于允许值1.3。优化方案在现场进行应用，取得了较好的效果。