基于可预测适合度的选择性模型修复
2022-11-11张力雯方贤文邵叱风王丽丽
张力雯 方贤文 邵叱风 王丽丽,3
1(淮南师范学院机械与电气工程学院 安徽淮南 232038) 2(安徽理工大学数学与大数据学院 安徽淮南 232001) 3(嵌入式系统与服务计算教育部重点实验室(同济大学) 上海 201804)
过程挖掘技术是从信息系统所记录的事件日志中提取知识发现过程模型,并通过提供技术和工具对其实现性能上的改善.过程挖掘技术主要从3个方面对业务流程进行分析:过程发现、服从性校验、过程完善,其中服从性校验与过程完善之间有着密切的联系[1-3].模型修复是过程完善的一种,其旨在使事件日志能够回放于过程模型,且修复后的模型与初始模型尽可能相似.通常使用一致性校验的4个度量标准来对模型修复方法的性能进行评估,即适合度(fitness)、精度(precision)、简化度、泛化度[4].适合度是指事件日志在过程模型上的回放程度,而精度则描述了回放形式的准确程度[5].能够回放的活动不一定被准确回放,而准确回放的活动一定可以被回放.简化度决定了修复后模型的结构复杂性[6].泛化度表示修复后模型与初始模型之间的相似性,也就是说过程模型被限制为事件日志中可观测行为的程度.如果仅根据事件日志的可观测行为修复过程模型,则泛化度将受到影响;否则,过度泛化会降低精度造成欠拟合的情况[7].模型修复主要处理使得事件日志无法在过程模型上正常回放偏差活动,因此适合度和精度是评估其性能最为重要的2个指标[8-9].
模型修复通过一致性校验的方式检测事件日志回放于过程模型时产生的偏差,并基于这些偏差信息对过程模型进行修复[10-11].一致性校验主要包括迹对齐与行为关系匹配2种方法,且最优对齐是迹对齐中最优的一种检测方式[12-13].行为关系匹配用于发现对应活动之间不同的行为关系,也就是产生偏差的非拟合行为[14].最优对齐能够检测出事件日志与过程模型之间发生次数最少的偏差,并确定其具体发生位置.通过层层排除的方法构建最优对齐,并根据偏差的不同单位成本进一步分析其最优性,从而获得任意业务流程的最小偏差成本[15].模型修复通常基于偏差信息执行相应的操作,其中主要包括2种类型的偏差[16]:1)事件日志产生的可观测偏差,该偏差的修复形式同时影响适合度与精度;2)过程模型产生的偏差,其会阻碍事件日志正常地回放,这种偏差的修复形式仅对适合度有影响.就平衡适合度与精度而言,需要考虑第1类偏差的修复问题,现存技术主要对这类偏差采用2种修复形式:1)以自循环的方式将可观测偏差插入过程模型;2)构建偏差与隐变迁的冲突子结构,并将其添加于过程模型的合适位置.前者无法准确回放非迭代的可观测偏差,而后者不能回放迭代的可观测偏差,因此适合度与精度始终无法得到很好的平衡[17].由于循环路径的重复性,因而使得一些相同的偏差不断地发生.现存方法通常没有单独对循环部分的修复问题进行分析,而是采用与非循环部分一致的修复方法.因此,当事件日志与过程模型之间存在循环路径产生的偏差时,很容易在改善适合度的同时导致精度成倍地下降.理想的修复性能是在合理程度上保证适合度的同时尽可能提高精度,且不增加修复活动的数量(拥有相同标签和位置的所有偏差被视为一个修复活动).值得注意的是,为了准确计算适和度与精度,每一个需要被修复的偏差活动都被看作一个独立的单位成本进行核算(其中包括偏差的迭代发生)[18].
图1使用业务流程模型与标注(business process model and notation, BPMN)描述了一个投保流程的模型M.M在信息系统中会不断变化,并被记录为一个事件日志L={(a1,…,an)1,(a1,…,an)2,…,(a1,…,an)m}.其中,(a1,…,an)1,…,(a1,…,an)m表示从初始活动a1到终止活动an之间所有活动组成的m条迹,L则为m条迹的集合.图1设定L={(ABEIIIJK),(ABFJIIIK),(ACDGGGHIJK),(ADCGHIJK)},统一使用A到K之间的字母表示L中所有活动的对应标签.通过最优对齐可搜索到L与M之间非循环部分存在的3种偏差:1)L中的非迭代可观测偏差{D,G,I,J};2)M上能够捕获且使得L无法正常回放的偏差{D};3)L中的迭代可观测偏差{I2,G2}(偏差右上角的数字表示事件日志中偏差自身迭代发生的次数).将偏差活动的单位成本设置为1,可计算出L与M之间的适合度和精度分别为fitness=1-Devcost/(|L|+|ML|)≈0.67,precision=1(Devcost为偏差成本,|L|+|ML|为日志与模型在对齐过程中所有元素的个数).初始模型上没有自循环路径产生的迭代活动时,核算精度需要将日志预处理为与模型完全拟合的子日志,因而在这种情况下精度始终为1[19].上述第2类偏差均来自于M,因此其修复形式不影响精度.通过在此类偏差元素的原有位置添加隐变迁进行修复,可以使这部分的适合度得到完整提升.上述第1类和第3类偏差均来自于L,以自循环方式将其插入M进行修复,则第1类偏差无法被准确回放.修复后L与M之间的适合度为1,但精度却下降了0.32.将L中的偏差元素与隐变迁组建为一个冲突子结构,并添加到过程模型上的合适位置,该方法无法回放第3类偏差.修复后L与M之间的精度为1,但适合度却只有0.88.这种情况下,要么以大幅度牺牲精度为代价来保证适合度最终为1,要么精度为1但适合度则不够合理.
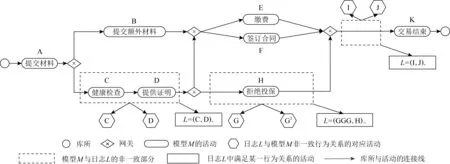
Fig. 1 Life insurance application process and deviations based on information system图1 人生保险申请过程和基于信息系统产生的偏差
本文针对如何同时兼顾适合度与精度对模型的修复问题主要进行了2方面的改进:1)根据迭代可观测偏差的总成本预测使用配置方法进行整体优化后的适合度,并当其满足给定阈值范围时确定对所有可观测偏差进行配置优化.2)当预测适合度不满足阈值时,利用行为关系的匹配性发现事件日志与过程模型之间存在的变体,并通过检测每个变体中是否包含迭代可观测偏差来执行合适的操作.由于低频过滤不在本文的研究范围之内,因此本文默认事件日志是已经过滤后的有效事件序列集.
1 相关工作
本文所提出的方法主要涉及模型修复与配置优化2种技术[20-21].模型修复的目标是使事件日志能够在修复后的过程模型上回放,并尽可能地维护原始模型的特有行为.采用伪布尔约束来处理多目标问题,该方法以最小代价实现了模型的最大回放[22].与自动操作相比,手动修复可以尽可能地避免过程模型中不必要的冗余行为[23].上述伪布尔约束方法和手动修复方法在合理提高适合度的同时尽可能降低修复成本,但其忽视了一致性度量中的其他重要标准,即精度.将定义的扩展对齐添加到过程模型的可达标记中,计算模型中的偏差并对其进行修复[24].通过Petri网和各选择结构之间的转换关系确定模型的修复位置[25].上述2种方法综合考虑了各种度量标准的改进,但仅适用于选择结构的网系统.将多个经典问题的解决方案用来搜索事件日志与过程模型之间所需的修复活动,旨在以最小的代价处理最多的偏差[26].这种方法需要牺牲大量精度来换取适合度的提升.基于4个度量标准分析过程模型的修复方法,并将满足并发关系的可观测偏差子结构以自循环方式插入到过程模型上,其在一定程度上改善了修复后的精度,但仍然无法对非迭代插入偏差进行准确修复.在保证适合度为1的前提下根据当前变体的实际情况选择执行不同的操作,其往往由于过分追求适合度而导致精度仍然可能存在不合理的现象[27].
配置优化在给定约束条件下发现一个业务流程中具有共性的参考模型,并将其与变化模型之间产生的变量进行兼容[28-29].这种技术通过在控制流中添加/移除可配置活动的选择子结构来实现优化[30-31].基于事件日志所记录的真实行为构建可配置片段,并通过对其进行优化获得一个具有共性和个性行为的过程模型[32].配置优化技术构建日志中可观测偏差与隐变迁的冲突子结构,并通过将其添加到过程模型的合适位置实现修复[33].使用这种方法不能回放日志中自循环路径产生的迭代可观测偏差,因而无法保证修复后的适合度在合理范围内.本文首先对整体配置后的适合度进行预测,并根据阈值条件选择是否对初始模型执行整体配置.当不能进行整体配置时,需要发现事件日志与过程模型之间的变体,并根据每个变体中是否包含迭代可观测偏差选择执行不同的操作.循环部分的修复要根据循环中产生偏差的不同情况来执行,从而最大程度地兼顾适合度与精度.
2 准备工作
定义1.事件日志.将元组L=(κ,q,e,ϖ,,∠)记为事件日志,其中包含事件日志L的元组中包含所有可能出现的符号标注.κ为日志中的一条迹,q为多重迹的统一案例号.由于事件日志中可能存在不同的多重发生迹,因此其中所有案例号都属于一个案例集q*,即∀q=q*.e为日志中的事件元素,记作∀ei∈L.ϖ为事件日志中所有事件的标签集,且将每个事件指定为其对应的标签,为相邻事件之间的流关系,记作∠⊆E×E.
定义2.标签工作流网系统.将元组N*=(P,T,F,Z,λ,δ,D,pini,pfinal)定义为标签工作流网系统.P,T,F分别表示网系统N*上的库所、变迁以它们之间的流关系,F⊆(PF)∪(FP).Z为网系统N*中所有变迁的标签集,且λ将每个变迁指定到对应的标签,为网系统上从初始结点到终止结点之间的一条完整序列,d为每条序列δ的案例号,记作δd.由于网系统N*中可能存在不同的序列,因此其中所有发生序列都属于一个序列集即与pfinal∈P分别为工作流网的初始库所与终止库所,当且仅当|pini|=|pfinal|=1时网系统N*为工作流网.
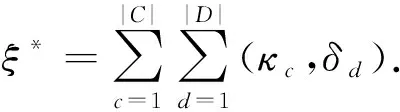
定义4.拟合模式与非拟合变体.非拟合变体是指引起事件日志与过程模型之间部分偏差的对应子模式[34].在最优对齐中划分由不同行为变化所产生的偏差,并根据每个行为变化中的活动在所有对齐中的行为关系确定变体类型.
例如,L={(ABCDEFGHK),(ACBDEFGHK)}被回放于过程模型上,该过程模型的发生序列集为δ*={(ABCDEIJK),(ABCEDJIK),(ABCDEIJK),(ABEDJIK)}.图2中找出3组偏差(B,C),(F,G,H),(I,J)分别属于并发/因果、插入因果行为包含及跳过因果行为包含的变体,记作v(C,D)L+∧N*,v(F,G,H)L⊆,v(I,J)N*⊆.值得注意的是,事件日志或网系统N*中单个出现的偏差可被看作一个独立的变体,记作vL‖N*((ei)‖λ(ti)).图2中B=(D,E)和Bfit(a)=(A,K)表示事件日志与过程模型之间拟合的行为模式,其中B=(D,E)为拟合的因果行为模式,而Bfit(a)=(A,K)则是单个活动的拟合行为模式.
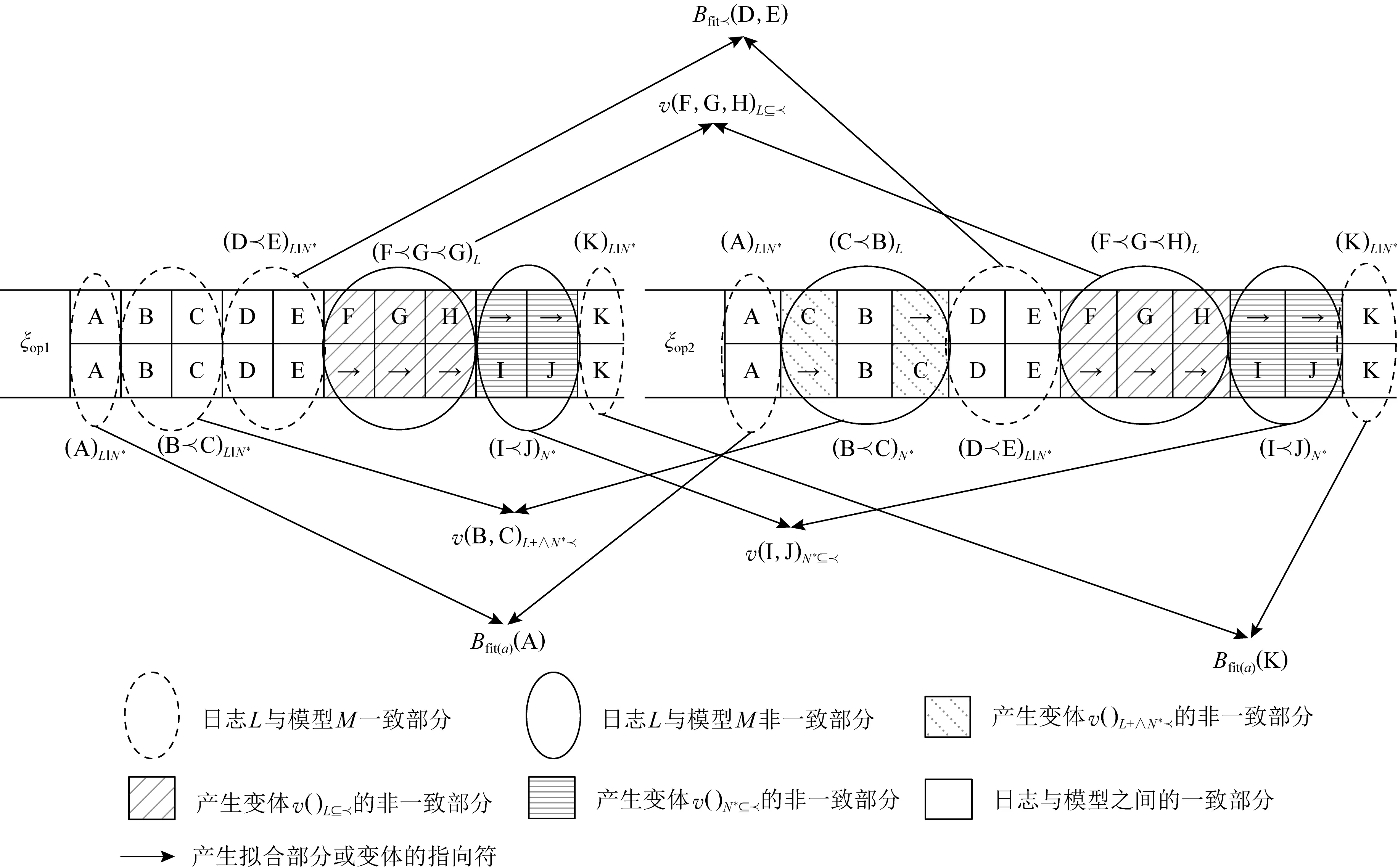
Fig. 2 Search for variants based on optimal alignment图2 基于最优对齐搜索变体


Fig. 3 Examples of repair operation and configuration operation图3 修复操作与配置操作的实例
定义6.修复操作与配置操作.修复操作利用最优对齐检测偏差的完整信息,并采用自循环插入日志中的偏差或隐变迁跳过模型中的偏差对网N*进行修复.根据偏差的不同结构类型,可将修复操作分为2种:1)单个活动的修复操作RO=sl_Esert(ei)或者RO=Skipλ(tj);2)子结构的修复操作RO•=sl_E((e1),…,(ei))或者RO•=Skip(λ(t1),…,λ(tj)).图3(a)中描述了修复操作的实例.配置优化通常是对业务流程之间所有不匹配的行为进行优化,而本文则只考虑回放过程中非拟合行为变体所产生的差异.图3(b)所示的配置操作是在模型上添加日志中不可回放的行为或者通过隐变迁隐藏模型中阻碍日志回放的行为,并将配置操作执行的所有行为称作可配置行为[35].根据可配置行为的不同结构类型将配置操作分为2种:1)单个活动的配置操作是CO=Add((ei))=((ei),τ)×或者CO=Hide(λ(tj))=(τ,λ(tj))×;2)子结构的配置操作CO•=NAdd((e1),…,(ei)),+,×=(((e1),…,(ei)),τ)×或者CO•=NHide(λ(t1),…,λ(tj)),+,×=(τ,(λ(t1),…,λ(tj)))×.
3 操作确定及故障诊断
事件日志与过程模型在实际运行中可能会存在一些不被期望的非一致行为,其中模型修复主要对日志回放于模型所产生的非拟合行为进行处理.本节根据可预测适合度是否在给定合理范围内来确定不同的修复方案,并分别从2种角度对一个变体中的故障进行检测与分析.
3.1 确定不同情况下的修复方式
为了尽可能兼顾事件日志与修复后模型之间的适合度与精度,可设定适合度的合理范围,并在此范围内最大化提升精度.使用配置操作对初始模型进行整体修复后的新模型不包含迭代活动,且任意事件日志与该模型之间的精度值始终为1.然而,这种情况下所有迭代插入偏差不能被回放,以至于适合度可能会受到不同程度的影响.因此,当使用配置操作整体修复后的可预测适合度值低于合理范围时,需要发现事件日志与过程模型之间的变体,并根据每个变体的具体情况选择执行配置操作和修复操作[36].
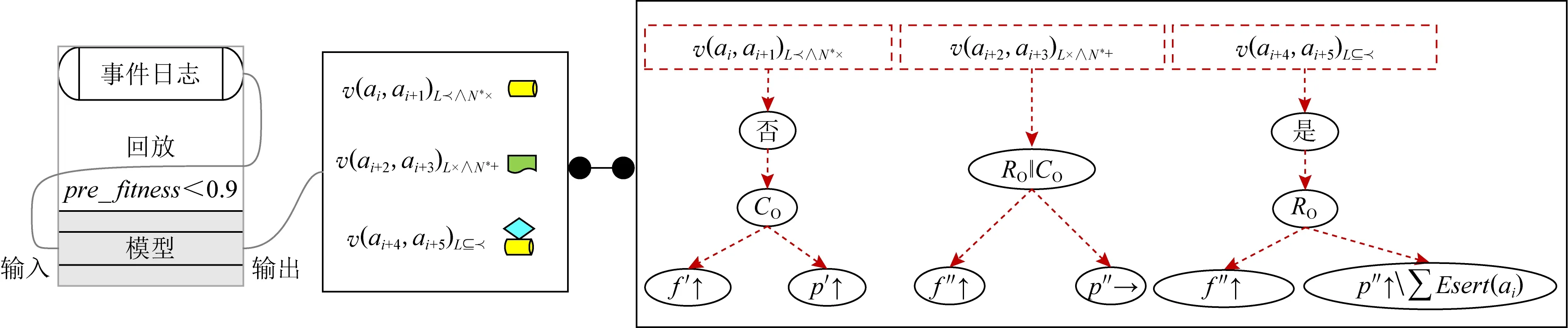
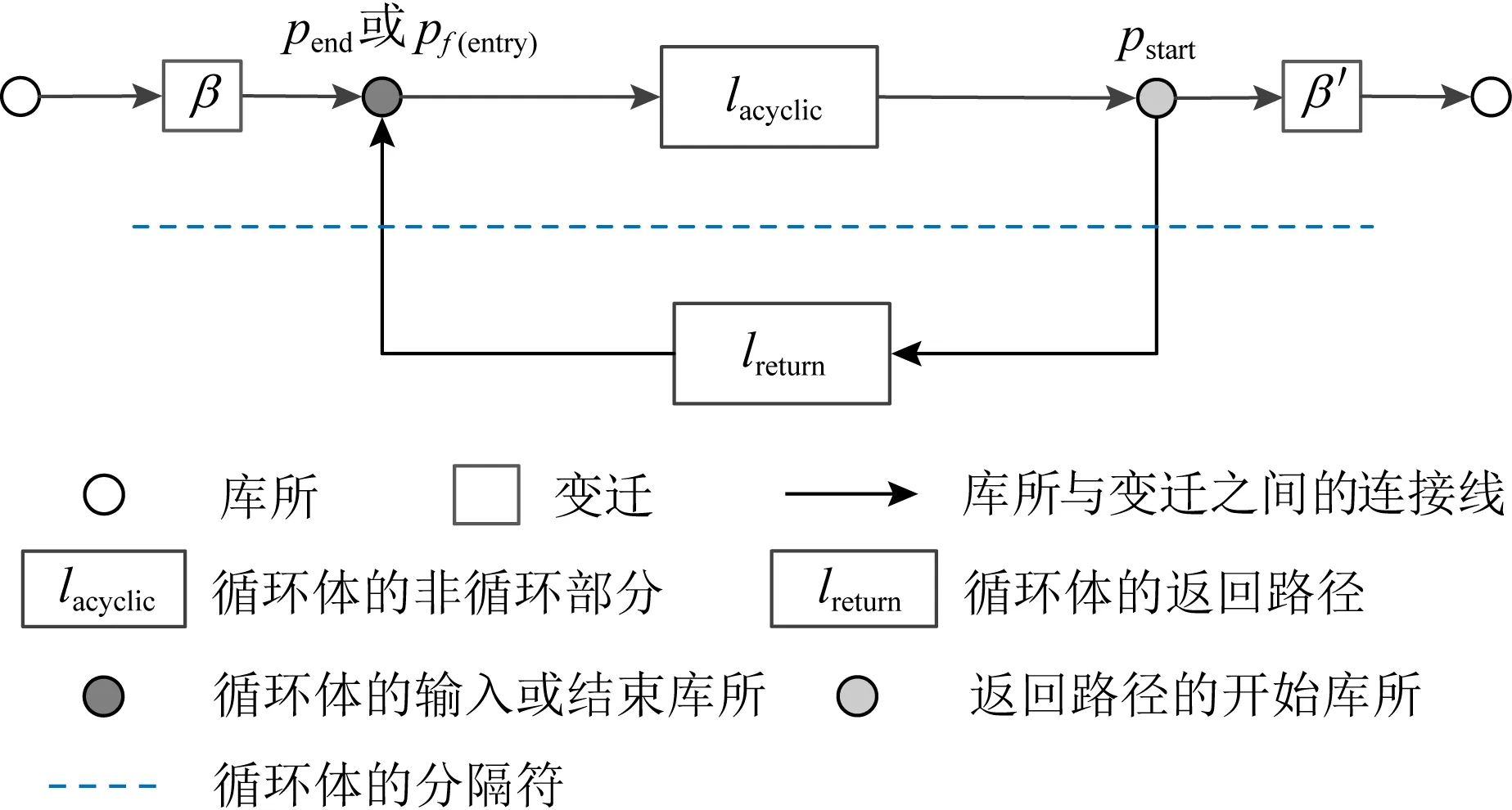
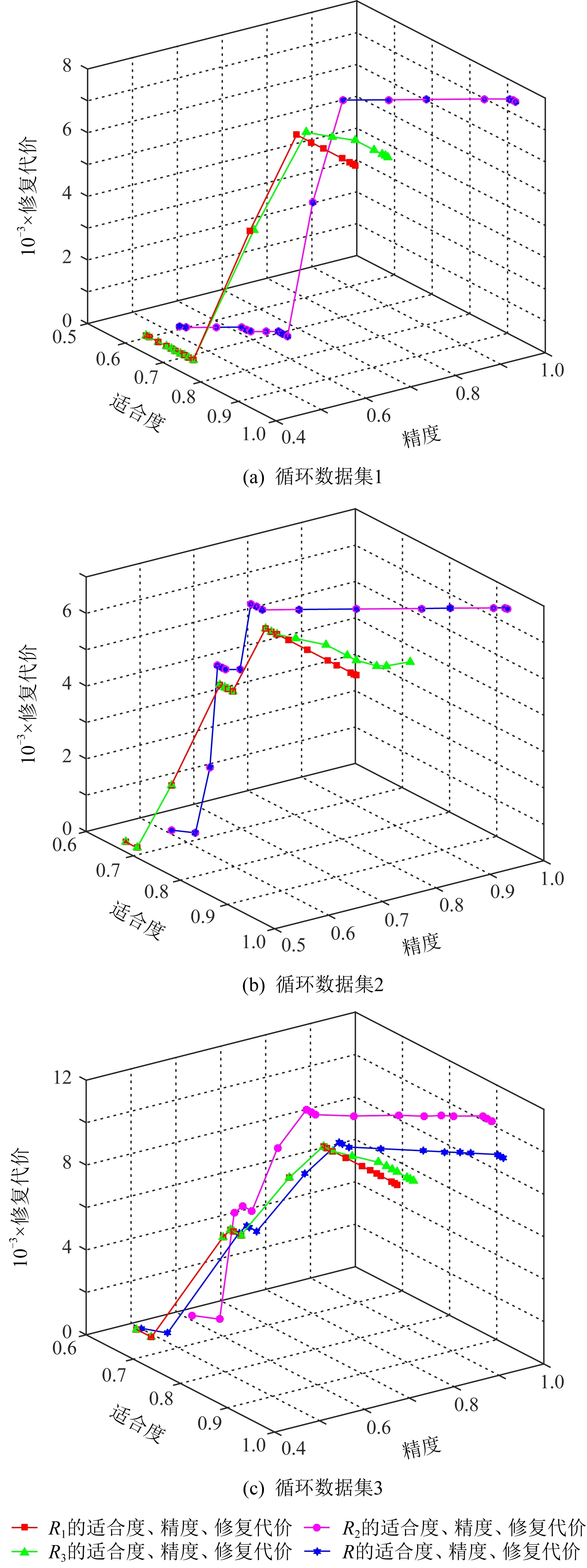
可预测适合度是指使用配置操作对初始模型进行整体修复后的适合度,其中所有迭代插入偏差无法被修复.根据迭代插入偏差总成本核算可预测适合度的公式为per_fitness=1-IDevcost/(|L|+|ML|),其中IDevcost为迭代插入偏差的成本函数.当pre_fitness≥0.9时,使用配置操作对初始模型进行整体修复(给定阈值被设置为0.9,且0.9 Fig. 4 The alternative principle for different operations图4 不同操作的选择原理 Fig. 5 Three optimal alignments图5 3组最优对齐 修复操作依赖于最优对齐检测到的偏差元素来优化过程模型,其中迭代插入偏差是一种特殊的偏差类型,即只有当日志记录的单个偏差元素经过自循环路径时才会发生[37].设定事件日志L回放于初始网系统N*={(ABCDG),(AEFG)}时产生了图5中的3组最优对齐. 根据图5中的3组对齐可获得一个变体v(C,D)L+∧N*,并且还有6个完全由自循环路径产生的迭代插入偏差,即ξop1中的IEsert(B)2,IEsert(C)1,IEsert(D)1和ξop2中的IEsert(B)1,IEsert(D)1,IEsert(C)1.由于它们在正常路径下不能发生,因此即使只发生1次也会被看作迭代插入偏差处理.ξop2中的插入偏差IEEsert(D)2既产生于并发/因果的变体也产生于自循环路径,且ξop3中的非迭代插入偏差Esert(D)包含于ξop2中的迭代偏差IEEsert(D)2.值得注意的是,ξop2中有来自于变体v(C,D)L+∧N*的插入偏差,其可与IEsert(D)1合并在一起,并记作IEEsert(D)2(根据定义5可知,IEEsert(D)2中D的迭代次数为1). 配置是一种将参考模型与定制模型之间不匹配行为相互兼容的优化技术.在发现可配置行为的过程中,将事件日志看作是不含有迭代插入偏差的一个参考过程模型,而给定过程模型则是一个变化模型[38].为了能够更好地兼顾适合度与精度,在一定条件下需要基于可配置行为在初始模型上执行配置操作,从而完成模型修复的功能. Fig. 6 Execution program and effect of real-time repair图6 实时修复的执行方案及效果 设定事件日志与过程模型之间的变体分别为{vL(ad),v(ag,ah)L×∧N*+,v(ai,aj)L⊆+},其中vL(ad)为仅日志中可观测到的单个活动变体,因而被看作一个可配置活动Add(ad).v(ag,ah)L×∧N*+可展开为(agHide(ah))‖(Hide(ag)ah),其中选择发生的可配置活动之间满足冲突行为关系,将它们构建为可配置的冲突子结构NHide(ag,ah)×.v(ai,aj)L⊆+展开为(Add(ai)Add(aj))‖(Add(aj)Add(ai)),其中直接跟随的可配置活动之间满足并发行为关系,将它们构建为可配置的并发子结构NAdd(ai,aj)+.配置操作根据定义6描述的方式在初始模型上对可配置活动或子结构进行修复.值得注意的是,当可预测适合度在合理范围时,无需发现事件日志与过程模型之间的变体,而是直接使用配置操作对初始模型进行整体修复.在这种情况下,将最优对齐检测出的迭代插入偏差移除,并使其余偏差转换为相对应的可配置行为. 适合度与精度是衡量业务流程一致性的2个重要依据,因此关于事件日志对过程模型进行修复时需要同时兼顾适合度与精度.修复操作与配置操作在修复中分别对适合度和精度进行优先考虑,使用其中一种操作对初始模型进行整体修复,往往会造成回放性能的改善过于局限.综上所述,为了能够合理地权衡适合度与精度,需要在修复初始模型时根据具体情况选择不同的操作. 事件日志与过程模型之间的可预测适合度在阈值范围之内时,需采用配置操作对过程模型进行整体修复.当可预测适合度不在阈值范围内时,则根据每个变体中是否包含迭代插入偏差选择修复操作或配置操作.本节介绍各种非循环部分产生变体的修复方式,也就是修复操作与配置操作的选择性执行.一个包含迭代插入偏差的变体中也可能存在非迭代插入偏差,因此需要执行修复操作.修复操作能够使这种变体中的所有插入偏差回放于过程模型上,但其中非迭代插入偏差不能被准确回放.另一方面,在不包含迭代插入偏差的变体中执行配置操作,可以使其中所有插入偏差被准确回放.图6首先判定可预测适合度不在合理范围内,并给定事件日志与过程模型之间存在的3个变体v(ai,ai+1)L∧N*×,v(ai+2,ai+3)L×∧N*+,v(ai+4,ai+5)L⊆.v(ai,ai+1)L∧N*×中包含插入偏差但没有迭代插入偏差,使用配置操作可完整提升该变体的适合度和精度.v(ai+2,ai+3)L×∧N*+中不包含插入偏差,因此使用修复操作或配置操作都能够完整提升它的适合度,且精度不受影响.v(ai+4,ai+5)L⊆中包含迭代插入偏差,使用修复操作可完整提升其适合度,但精度会由于非迭代插入偏差无法被准确回放而受到影响[39]. 如图7所示,L与N*之间的变体分别为v(C,D)L+∧N*,v(E,F)L+∧N*×,v(H,I)L⊆+,它们可选择的修复方式分为2种:1)弯虚线表示当前变体中含有迭代插入偏差时所做的修复操作;2)直虚线描述了当前变体中不包含迭代插入偏差时所做的配置操作(空心箭头连接的隐变迁表示修复操作与配置操作的共有部分).值得注意的是,当pre_fitness≥0.9时使用直虚线描述的配置操作对过程模型进行整体修复. Fig. 7 Repair instance of the acyclic part based on an optional operation图7 基于可选操作的非循环部分的修复实例 根据3.1节的方法检测出变体v(C,D)L+∧N*和v(E,F)L+∧N*×中含有迭代插入偏差,因此选择执行修复操作.由于变体v(H,I)L⊆+中没有迭代插入偏差,则选择执行配置操作.v(C,D)L+∧N*和v(E,F)L+∧N*×中包含的偏差分别为(IEEsert(D)3(21),Skip(D)1(21))和(IEEsert(F)3(9),Esert(E)1(2)),其中IEEsert(D)3(21)中3表示迭代次数,21表示迹发生的多重次数,该偏差元素的成本为3×21.v(H,I)L⊆+中包含的偏差为(Esert(H)1(7+21+9+2),Esert(I)1(7+21+9+2)).在v(C,D)L+∧N*和v(E,F)L+∧N*×上执行修复操作后能够修复的偏差成本为84和29,而准确修复的插入偏差成本则为42和18,也就是说非迭代插入偏差Esert(D)1(21),Esert(F)1(9),Esert(E)1(2)无法被准确修复,且跳过偏差Skip(D)1(21)的修复不影响精度,因而不被计入需要准确修复的偏差中.在v(H,I)L⊆+上执行配置操作后能够修复的偏差成本为78,而能够准确修复的插入偏差成本也为78.综上所述,根据不同情况选择执行2种操作后的适合度与精度分别为fitness=1-和0.91.由于并发行为中活动发生顺序的随机性会使配置回放图表的结构较为复杂,因此当vL+∧N*和vL+∧N*×中的活动个数大于2时,可分别根据图8和图9中描述的方式寻找配置操作CO,并确定其具体位置.图8和图9中使用矩形方框来标注vL+∧N*和vL+∧N*×所对应的配置操作CO. Fig. 8 Search for configuration operation in concurrency/causality variant图8 搜索并发/因果变体中的配置操作 Fig. 9 Search for configuration operation in concurrency/conflict variant图9 搜索并发/冲突变体中的配置操作 非循环部分的变体主要由非一致的行为轮廓关系和行为包含产生,算法1描述了非循环部分产生变体的配置操作与修复操作. 算法1.非循环部分产生变体的选择性修复. 输入:网系统N*、事件日志L、所有偏差之和∑d、迭代插入偏差的成本判定函数ψ、选择任意一个或几个元素的函数σ、配置操作cO(cO∈CO)、修复操作rO(rO∈RO); 输出:配置操作集CO、修复操作集RO. ①CO←∅,RO←∅; ② for eachei∈Ldo ③ for eachtj∈Tdo ④ for eachak∈Zdo ⑤ ifpre_fitness=1-IDevcost/(|L|+ |ML|)≥0.9 then ⑥CO(∑d); ⑦ else ((a1,a2)‖((a1,a2,…,an), (an+1,an+2,…,an+m))) then ⑨ ifψ(IDevcost)=0 then ⑩cO1←(Add(a2)∪Hide(a2)) ‖(NSkip∪sl-Esert(an+1,an+2,…,an+m)∪sl_Esert(σ(a1,a2,…,an+m))); vL×∧N*+(a1,a2) then (Hide(a1)∪Hide(a2)); Nsl_Esert((a1,…,an),(an+1,…,an+m))×) ‖rO2cO2; (Hide(a1)∪Hide(a2))); rO3cO3; τ)×τ)/(τ(τ, (NHide(a1,a2)‖+‖×,τ)×τ)); rO4cO4; 算法1中,将空集赋予配置操作与修复操作的集合CO,RO(行①).首先判定可预测适合度是否在合理范围内,如果在合理范围内则统一使用配置操作修复所有偏差(行⑤~⑦).当可预测适合度不在合理范围内时,根据以下不同变体中是否包含迭代插入偏差选择合适的操作:1)构建并发和因果行为关系产生变体的配置操作(行⑧~)或修复操作(行);2)构建并发和冲突行为关系产生变体的配置操作(行~)或修复操作(行);3)构建因果和冲突行为关系产生变体的配置操作(行~)或修复操作(行);4)构建3种行为包含产生变体的配置操作(行~)或修复操作(行).由于迭代插入偏差的发生是随机的,因此所有自循环插入偏差的情况都被关联于修复操作集中,即RO(V(L+∧N*),(L+∧N*×),(L∧N*×),(L⊆,+,×))←χ.不包含插入偏差变体的修复操作与配置操作可互换,即RO(V(L×∧N*+),(L×∧N*),(N*⊆,+,×))←CO(V(L×∧N*+),(L×∧N*),(N*⊆,+,×)).最后,返回可能在因果、并发、冲突、行为包含引起变体中执行的所有配置操作集CO与修复操作集RO. 循环部分的修复首先需要识别其所发生的位置,由于长度为1或者2的短循环可通过∂+算法来识别[40],因此这里仅对包含3个及以上活动的循环进行分析.设定pstart…lreturn…pend为一条循环路径,其中pstart和pend分别表示循环路径上的起始库所与结束库所,lreturn表示返回路径上的行为模式.loopbody=(pf(entry)…pstart,pstart…lreturn…pend)表示一个完整的循环体,也就是循环中所包含的所有活动以及它们之间的行为关系,其中pf(entry)…pstart为非循环部分.判定一个循环体结构的存在需要满足2点:1)循环体输入库所pentry的因果后置库所pf(entry)与结束库所lend是一致的,即pf(entry)=pend;2)pf(entry)的执行配置尺寸小于pend,记作pf(entry)=pend∧C(pf(entry)) Fig. 10 Path partitioning of the cyclic part图10 循环部分的路径划分 通过一个不等式来描述返回路径上的活动: 循环部分可能出现的变体有3种:1)只有事件日志中含有循环路径;2)非循环部分存在变体(这个问题在4.1节进行讨论);3)返回路径上存在变体. 修复循环部分需要根据以上3种情况产生的变体执行操作,本节在不考虑非循环部分的情况下对其中2种进行分析: 2) 事件日志与过程模型中都含有循环路径,但在返回路径lreturn上的行为不一致.例如,图11(b)所描述的网系统N*中的循环路径是lend…lf(entry)=D/C…B/C,而事件日志L中的循环路径则为lend…lreturn…lf(entry)=D/C…E(A)…B/C,由此产生变体vL(E(A)).图11(b)中使用弯虚线描述了vL(E(A))中含有迭代插入偏差时对网系统N*所做的修复操作,其位置为loc(Esert(E))∪loc(τ)=p6∪(p6~(p1∪p4)).反之,则采用直虚线所表示的配置操作,其位置为loc(Add(E))=((pC1∪pC3)~(pC2∪pC4)). 当上述第1种情况下非循环部分一致,且返回路径上没有活动存在时,2种操作都直接使用隐变迁连接循环路径,从而准确回放当前变体中的所有偏差.值得注意的是,如果可预测适合度在合理阈值范围内,则对循环部分统一实行直虚线描述的配置操作. 算法2是在默认非循环部分可回放的前提下,构建循环路径产生变体的2种操作.首先,将空集赋予循环路径的修复操作集COloop和配置操作集ROloop(行①).根据网系统N*是否包含循环路径分2部分进行讨论:1)仅事件日志包含循环路径,此时若返回路径上没有活动则修复操作与配置操作相同(行⑤~⑥).当返回路径上存在活动时,判定可预测适合度是否在合理范围内,如果在合理范围内则统一使用配置操作修复所有偏差(行⑦~),如果不在合理范围内就根据循环变体中是否包含迭代插入偏差选择合适的操作(行~).2)事件日志与网系统都包含循环路径时,仍需要判定可预测适合度是否在合理范围内,如果在合理范围内则统一使用配置操作修复所有偏差(行~),如果不在合理范围内就根据具体情况在返回路径上执行配置操作和修复操作(行~).最终,返回对循环路径上所有情况下可能执行的配置操作集COloop与修复操作集ROloop(行). 算法2.循环部分产生变体的选择性修复. 输出:配置操作集COloop、修复操作集ROloop. ①COloop←∅,ROloop←∅; ② for eache∈Lloopdo ③ for eacht∈Tdo ④ for eacha∈Zdo ⑤ iflend…lf(entry)∈Lloop∧lreturn=∅ then ⑦ end if ⑨ ifpre_fitness≥0.9 then ⑩CO(∑dloop); 对包含迭代插入偏差的变体执行修复操作,无法准确修复其中所有的非迭代插入偏差.针对这一问题,将此类变体中满足一定行为关系的非迭代插入偏差构造成子结构[42].多个偏差被看作为一个整体会减少事件日志中需要被修复的插入偏差个数.这种方法对于精度改善的逻辑表达式为 Esert((e1),(e2))+/→ 其中,E_Devcost为插入偏差的总成本,Esert((e1),(e2),…)+/表示在一个变体中满足并发/序列关系的偏差元素.插入偏差的个数不能通过冲突子结构减少,因而修复操作的偏差子结构仅由并发和因果关系组成. 实验将本文方法R与现存3种方法进行比较,并通过分析不同数据集上4种方法修复后的适合度与精度评估它们的性能.现存3种方法分别为:1)在过程模型上使用自循环的方式插入事件日志中可观测的单个偏差,记作R1;2)构建隐变迁与可配置行为的冲突子结构,从而将事件日志中可配置行为添加到过程模型,记作R2;3)构建满足并发/序列关系的插入偏差子结构,并使用自循环的方式将其插入过程模型,记作R3.值得注意的是,由于模型中跳过偏差的修复不影响精度,因而4种方法都使用隐变迁跳过的方式对其进行修复.部分现存模型修复方法的性能可以使用Prom框架进行验证,但它的原始代码并没有提供其他方法的改变部分.为保证实验结果的公平性,我们在此基础上使用Java语言编写程序验证4种修复方法的性能. Table 1 Information of Data Sets表1 数据集信息 为保证适合度与精度的改善能够被更加清楚地观测到,实验数据默认4种方法的精度初始值均为所有插入偏差都无法被准确修复的结果,并通过变体的逐个修复不断产生变化. 5.2.1 人造业务流程数据集的实验结果 图12中3个数据集的方法R可预测适合度分别为0.76,0.89,0.84,因此R需要通过校验各种变体中是否包含迭代插入偏差,并根据校验结果选择合适的操作对每个变体进行修复.R2使用配置操作对所有偏差进行修复,因此能够使精度最终为1.然而,R2不能修复迭代插入偏差,以至于适合度无法得到保证.R2修复后的适合度分别为0.76,0.89,0.84,且均不在适合度的合理范围内.R能够修复所有偏差,但不能准确修复包含迭代插入偏差变体中的非迭代插入偏差.因此,包含迭代插入偏差变体中的非迭代插入偏差成本占比越小,R的精度就越高.图12(b)中包含迭代插入偏差变体中的非迭代插入偏差成本在总成本中的占比最小,因此其修复后的精度比图12(a)(c)分别高出0.16和0.19.相较于R1,R3来说,R能够准确修复不包含迭代插入偏差变体中的所有非迭代插入偏差.因此,在适合度一样的前提下R修复后的精度始终高于或等于R3,且R3始终高于或等于R1.图12中的结果表明,提出方法R在确保适合度合理的情况下,精度在4种方法中最高. Fig. 12 The running results of an artificial business process图12 人造业务流程的运行结果 5.2.2 真实业务流程数据集的实验结果 图13(a)(c)中方法R的可预测适合度分别为0.86和0.83,因此需要切换执行2种操作修复不同的变体.图13(a)中使用R修复后的精度远高于R1和R3,这是由于这个数据集中迭代插入偏差在总偏差成本的占比最大.如图13(c)所示,虽然R1与R之间精度的差异很大,但R3与R之间精度的差异却仅为0.05.这是由于图13(c)的数据集中能够组建为子结构的偏差最多,其可以有效减少日志中需要修复的插入偏差个数.图13(a)(c)中,使用R2修复后的适合度为0.86和0.83,因而不在合理范围内.图13(b)中R的可预测适合度为0.95,因此使用配置操作对所有偏差进行修复.这种情况下R2和R修复后的适合度与精度相同,也就是适合度为0.95而精度则能够达到1.图13中3个数据集的结果均显示,提出方法R能够在保证适合度合理的前提下使得精度达到最高. Fig. 13 The running results of an real-life business process图13 真实业务流程的运行结果 5.2.3 有循环数据集的实验结果 图14中描述了有循环数据集的修复性能,结果表明使用提出方法R修复后可在保证适合度合理的情况下使精度最优.图14(a)(b)中方法R的预测适合度均为0.92,并使用配置操作修复所有偏差.图14(c)的预测适合度为0.89,则需要根据当前变体是否包含迭代插入偏差选择合适的操作.由于循环可能产生很多重复的偏差,因此当非循环部分产生变体中不包含迭代插入偏差时,会造成使用R与R1修复后的精度差异很大.迭代插入偏差成本在总偏差成本中占比越小,R与R1之间精度的差异越大.图14(b)中迭代插入偏差的占比比图14(c)低0.09,然而图14(c)中R相较于R1在精度上的改善反而比图14(b)高了0.04.造成这种情况的原因为图14(c)中仅事件日志中有循环,且其返回路径上无活动.因此,R与R1,R3都使用隐变迁连接循环路径,从而使3种方法对这种循环产生的偏差具有相同的修复效果. Fig. 14 The running results of an business process with loop图14 有循环路径的业务流程运行结果 召回度是指修复后模型能够回放的偏差成本在总偏差成本中的占比,准确度是指能够准确回放的偏差成本在总插入偏差成本中的占比,修复活动是指修复过程中不同标签或不同位置的偏差个数.选择图13(a)、图14(b)(c)中的3个数据集进行验证,图15(a)(c)中方法R的数据集的可预测适合度分别为0.86和0.89,R1,R3,R的召回度最终都能够达到1,且R的准确度高于R1,R3.然而,图15(a)和15(c)中R2受迭代插入偏差无法被修复的影响,它们的召回度分别为0.55和0.71.图15(b)中方法R的数据集的可预测适合度为0.92,R2与R的召回度均为0.78,且准确度为1. Fig. 15 Recall, accuracy, and number of repair activities图15 召回度、准确度以及修复活动个数 本文提出一种新的方法来修复事件日志无法回放于过程模型的行为,并根据不同情况选择合适的修复方式.该方法能够在确保适合度合理的前提下,尽可能改善精度,其主要从3方面进行分析: 1) 根据迭代插入偏差预测适合度,并设定合理的阈值范围. 2) 预测适合度合理时,使用配置操作对所有偏差进行修复,从而能够很好地兼顾适合度与精度.反之,则需要发现事件日志与过程模型之间的变体,并检测每个变体中是否包含迭代插入偏差. 3) 一个变体包含迭代插入偏差时,将其中所有直接跟随的非迭代插入偏差根据行为关系构建为子结构,并执行修复操作.反之,则对其执行配置操作.由于本文的修复方法将配置优化引入到模型修复中,因此使部分修复后的变体在精度上得到完整提升. 此外,本文将循环路径的修复问题单独提出,根据循环路径产生变体的不同类型从3方面进行分析.这样可以针对不同情况对修复方案进行调整,从而进一步改善循环部分的修复性能. 作者贡献声明:张力雯调研相关文献,确定文章的创新点,撰写文章,设计实验方案;方贤文把控文章的创新点,对文章内容进行修改与凝练;邵叱风完成文章的实验;王丽丽检查文章,配合完成实验.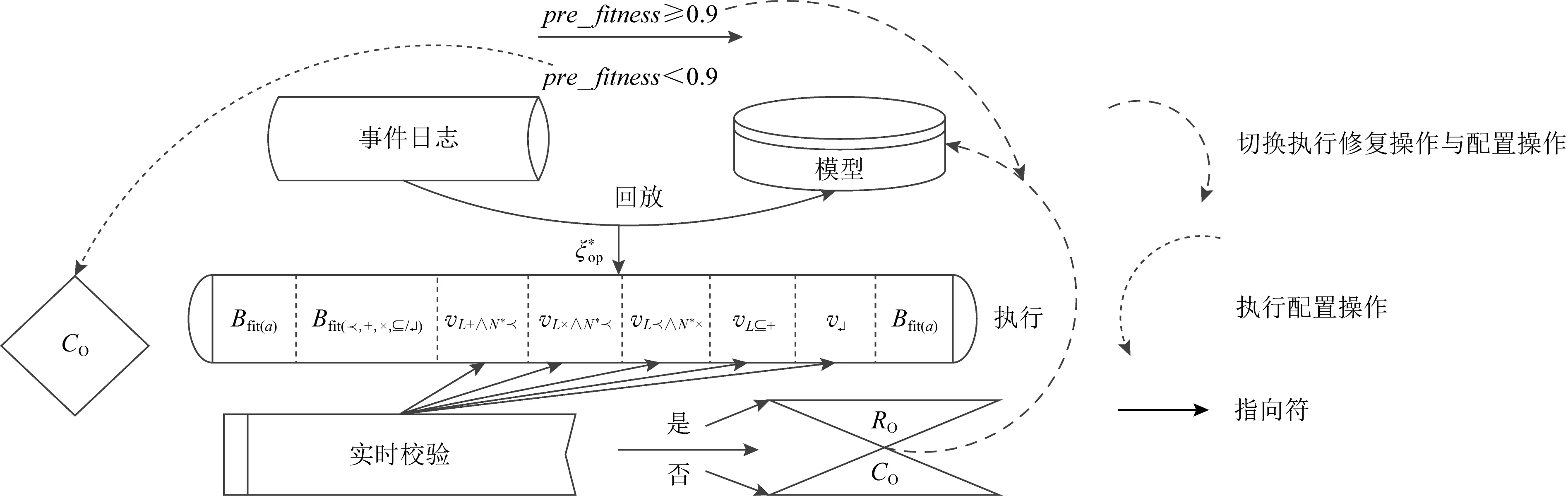

3.2 检测偏差
3.3 识别可配置行为
4 基于可预测适合度的选择性修复
4.1 非循环部分的选择性模型修复
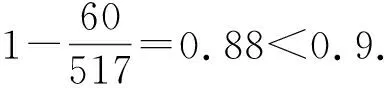


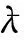
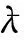


4.2 循环部分的模型修复


4.3 基于偏差子结构改善修复操作
5 评 估
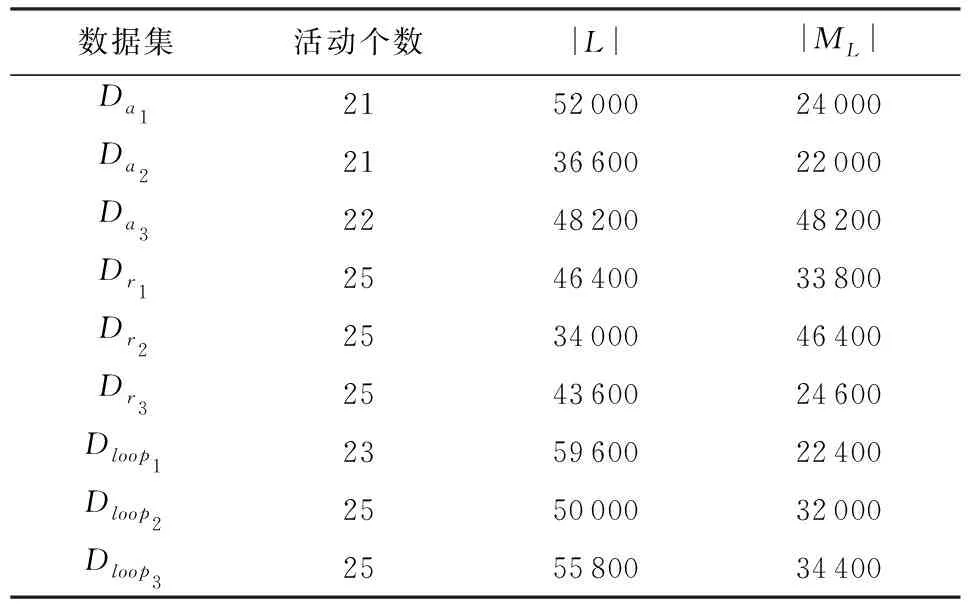
5.1 数据集

5.2 实验结果


5.3 召回度、准确度以及修复活动的数量

6 总 结
