燃气轮机旋向槽-迷宫密封结构设计与动力学分析
2022-11-10周金海焦映厚曲秀全
张 翔 , 周金海 , 焦映厚 , 曲秀全
(哈尔滨工业大学 机电工程学院,哈尔滨 150001)
0 引言
燃气轮机和汽轮机被称为制造业王冠上的珍珠,是传统工业中最为复杂的两套动力系统,被广泛应用于火力发电、船舶、航空等领域。传统的燃气轮机通常由压缩机、燃烧室和涡轮机部件组成。在燃气轮机内部复杂的轮系结构中,定子和转子之间均存在一定的间隙,以防止初始微小的扰动带来碰撞事故的发生。然而,由于该间隙的存在,压气机及涡轮内部的工质会产生一定的泄漏,降低整个机组的运行效率和经济性。流体密封结构作为一种相对轻质的密封结构,可有效减少流体工质的泄露,成为燃气轮机和汽轮机的重要组成部分[1-2]。
密封结构的增加在降低泄漏量的同时,也带来了不同程度的气流激振力。气流激振力的存在会导致转子在运行过程中出现失稳,进而造成重大事故。故对于密封结构的设计,除了对泄漏量的控制,还需对密封转子系统的稳定性进行权衡。对此,国内外的专家学者进行了大量的理论、仿真以及实验分析。Alford[3]、 Black[4]基于密封气流激振力对转子密封系统的影响规律,先后提出了描述气流激振力最基本的八参数模型,及参照短轴承理论提出的考虑惯性质量项的密封力模型。Muszynska等[5]在此基础之上考虑了切向流带来的影响,提出了另一经典的Muszynska模型。此外,通过对密封腔室进行划分,并作为整体单元进行考虑的控制体模型[6],也被证实具有一定的应用价值。仿真分析方面,基于Fluent的瞬态求解器[6]与稳态求解器[7]均被应用于求解密封结构的动力学特性参数。而在实验分析方面,Childs所在的实验室自20世纪以来,对不同的密封结构,如光滑环形密封、迷宫密封、孔型密封、蜂窝密封、袋式阻尼密封等结构进行了详细的实验测试和分析[8-12],相关成果被美国国家航空航天局(NASA)收录作为燃气轮机设计的重要参考文献[13]。
自20世纪80年代以来,国内学者通过对经典模型的再现和验证[14-15],对流体密封问题进行了一系列研究,近年来取得了令人可喜的成果。何振鹏等[16]详细对比研究了不同截面形状的蜂窝密封在篦齿-蜂窝混合密封结构中的表现,得到了大间隙、高转速及高压比工况下篦齿-圆形蜂窝密封最具优势的结论。张元桥等[17-18]重点关注螺旋篦齿-刷式密封,探讨了刷式密封所处的相对位置对密封性能及动力学特性的影响规律,并详细对比了刷丝分别处于上、下游时混合密封结构的多工况性能。Cao等[19]通过数值模拟的方式,研究了一种使用超临界S-CO2气体作为工质的交错齿迷宫密封结构。Zhou等[20]则将轴向交错齿的设计思路应用在了周向腔室上,设计得到一种交错螺旋齿迷宫密封结构,交错排布引起的较高湍动能耗散带来了相比于传统迷宫密封更好的密封性能。
随着对密封结构研究的深入,专家学者已不再满足于较简化的模型和较简单的工况条件。李志刚等[21]针对单相和多相流工况下的环形密封结构研究进行了总结和展望,指出现有对于单相环形密封的研究所使用的实验测试、基于Bulkflow模型的数值计算与计算流体力学(Computational Fluid Dynamic,CFD)方法的仿真模拟手段已具有相对成熟的可行性,未来还需深入探讨更高效的抑振方法及提升多相流数值预测的精度。顾乾磊等[22]在使用实验测试与数值分析对迷宫密封临界稳定性进行研究的基础上,进一步探讨了人为施加预旋气流对传统迷宫密封动静特性的影响规律。顾乘璟等[23]也考虑了相似的预旋进口流体对蜂窝密封的动力学与泄露特性的影响规律,研究均表明负预旋工况能在不改变密封结构的情况下,有效降低交叉耦合刚度系数、提高有效阻尼系数,进而提升系统的稳定性。
由于传统迷宫密封、刷式密封及阻尼式的蜂窝、孔型密封等核心密封形式,已经被工业实践所检验具有一定的抑制泄漏的能力,现行对密封结构的改造一般也以上述类型密封为基础进行结构的优化升级。同时,针对不同形式密封的对比研究[24-25]可以发现,相比于周向腔体完全联通的传统迷宫密封结构,部分联通以及部分阻断的阻尼及类阻尼式密封均能获得更高的有效阻尼,且对于不同的预旋工况具有更敏感的适应性能,这为获得泄露性能和动力特性均能得到更大提升的新型密封结构设计,提供了研究基础和发展方向。
针对传统迷宫密封结构,设计并研究分析一种周向间隔布置数个特定开槽角度微槽的旋向槽-迷宫密封结构。通过Fluent软件的稳态求解器获得该新型密封的泄漏量及动力学特性,并与传统迷宫密封进行对比。在此基础之上计算不同设计参数下新型密封结构的特性变化曲线,为获得更优密封与动力学性能的密封结构提供可供借鉴的材料。
1 模型建立
1.1 旋向槽-迷宫密封结构设计
传统迷宫密封结构一般由一系列排布于定子或转子上的周向短齿构成,如图1a、图1b所示。气流从前端进入,通过多级密封齿顶端的节流效应与密封腔内涡流的耗散效应,将左端的高压来流能量进行耗散和转化,在右端出口端进入下一级工作部件或排放入大气。在实际运行过程中,由于转子自身的高速旋转,以及可能出现的涡动旋转,转子与密封之间的流场会拥有一周向速度,该周向速度也被称为环流速度。通过Muszynska[5]及后来众多学者的研究可知,随着环流速度的增大,密封-转子系统的稳定性将逐步降低。
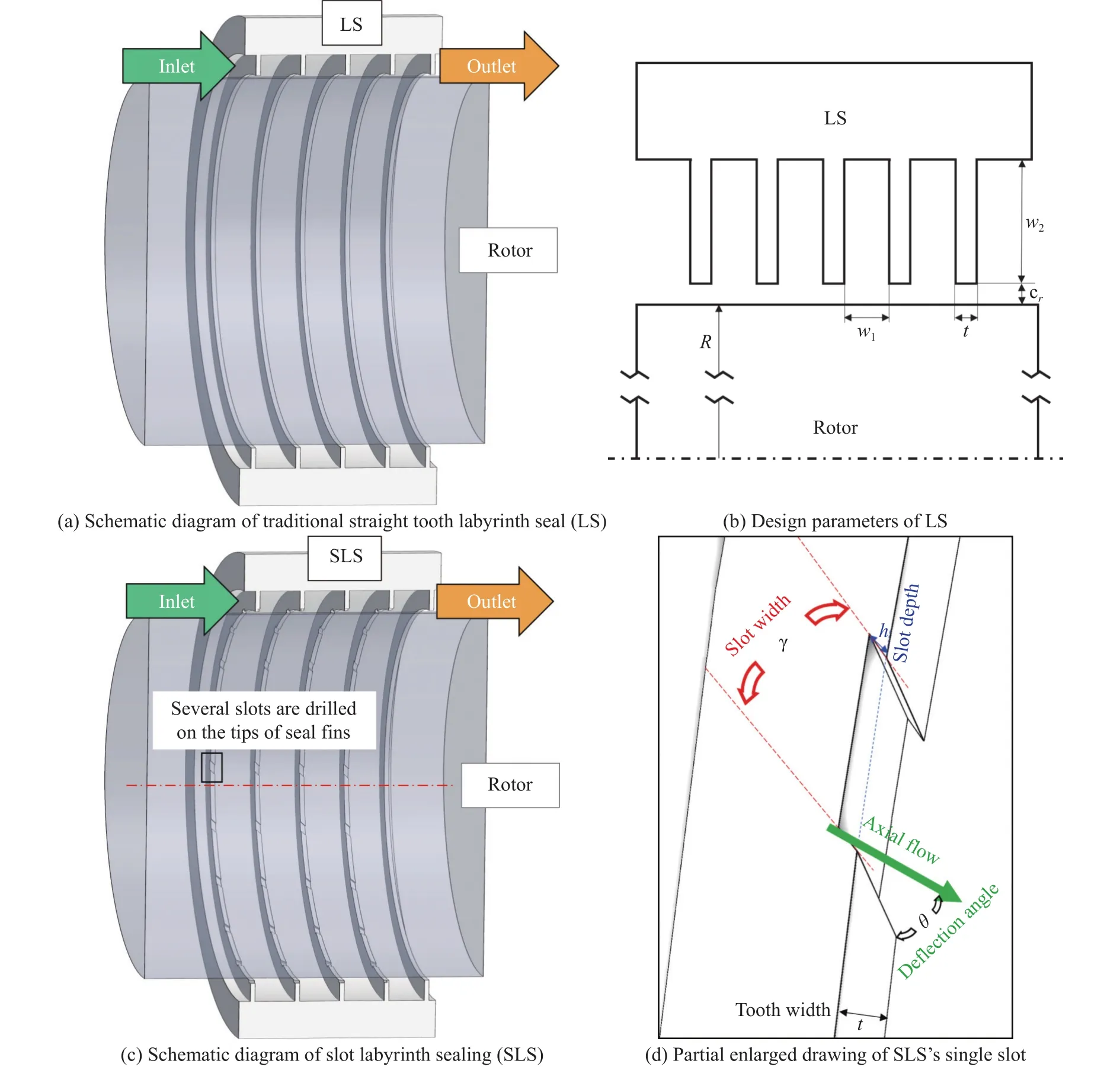
图1 传统直齿迷宫密封与旋向槽-迷宫密封示意图Fig.1 Schematic diagram and design parameters of traditional straight tooth labyrinth seal (STLS) and slot labyrinth seal (SLS)
本研究所提出的旋向槽-迷宫密封结构如图1c、图1d所示,是在传统迷宫密封的基础之上,在除最后一级密封齿外的每一级齿顶挖有一系列周向宽度为 γ、深度为h、 轴向偏转角为 θ的微槽。通过与转子自转方向呈反向偏转角 θ的微槽结构,对周向较大的环流速度进行一定的抑制,从而起到提高密封-转子系统稳定性的作用。表1列出了2种密封结构的结构参数。
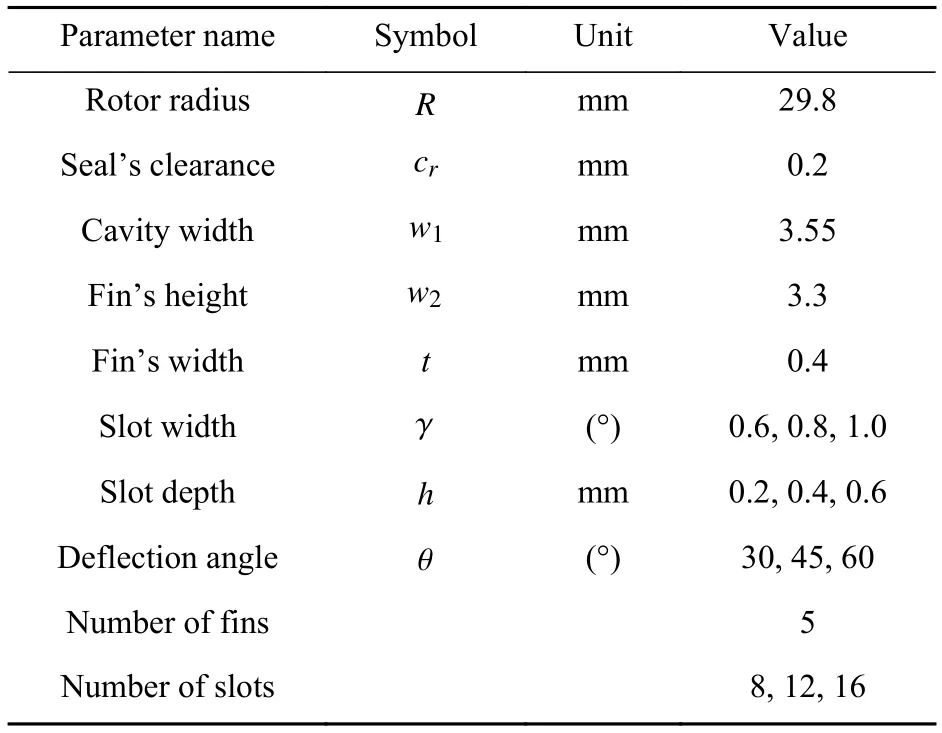
表1 2种密封结构的设计参数Table 1 Design parameters for two different seals
1.2 动力学建模
如图2所示,转子在实际运动过程中,会因为自身不平衡质量、非线性气流激振、非线性油膜激振等多重因素,使得转子中心与定子中心存在OOr的偏移,这一偏移一般使用e来表示,称为偏心距。由于偏心距的存在,工质气流在定子与转子之间的分布出现了不均匀现象,考虑定子固定时,该作用就可以被表征为转子受到的气流力F。
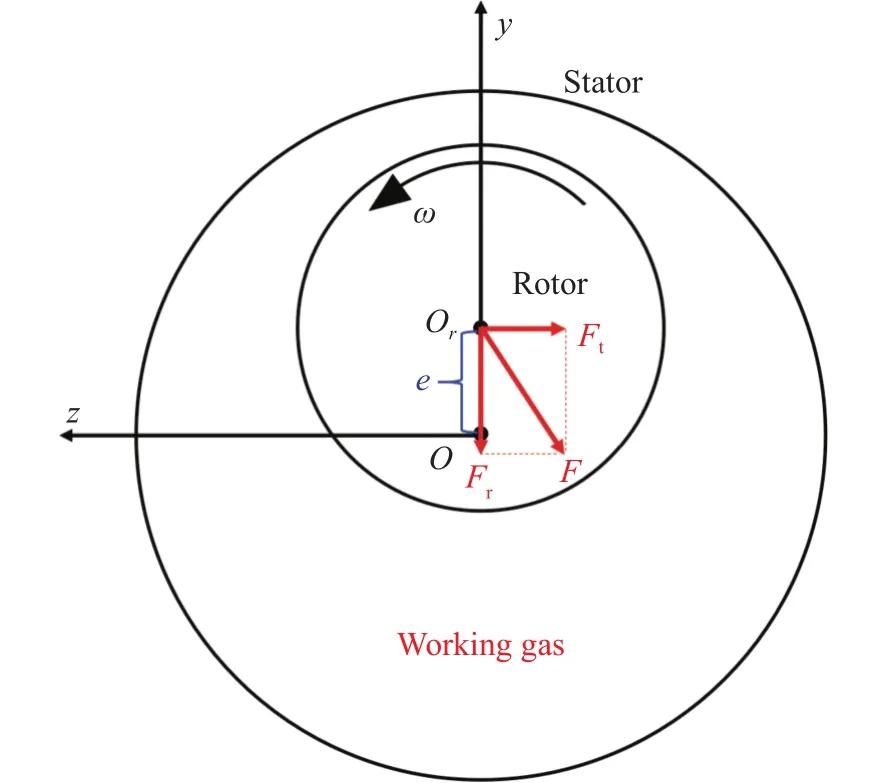
图2 转子运动模型Fig.2 Rotor-seal system model
F可以进行正交分解,分解为沿着偏心距方向的径向分量Fr和沿相对偏心距垂直方向的切向分量Ft。对于密封-转子系统,不考虑周向气流惯性因素的八参数模型被广泛应用于对密封结构的动力学特性进行描述,系统的动力学模型可以写为:
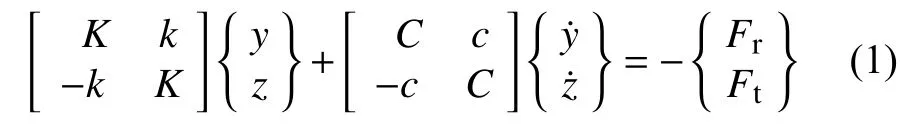
式中:K与k分别表示直接刚度系数与交叉耦合刚度系数,C与c分别表示直接阻尼系数与交叉耦合阻尼系数。假设转子以涡动角速度 2 πΩ进行涡动旋转,则式(1)中的位移与速度则可写成含涡动角速度的形式:

式中:T为考虑时域运动的时间参量。则此时径向力分量Fr与切向力分量Ft可被求得:
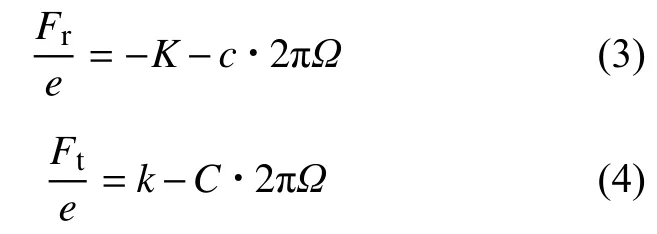
当不考虑涡动频率的影响(即 Ω =0时),又可进一步简化为:

综上,表征密封-转子系统稳定性的参数K与k可通过求解转子在无涡旋运动时受到的气流力直接求得。
2 仿真手段
有限元仿真是求解流体机械问题的一种高效方法,随着近些年CFD的发展,仿真求解的精度也得到了大幅提升,在边界条件、载荷、湍流模型等条件选取得当的情况下,所得到的结果已经具有足够的精确度。
本文使用ANSYS Fluent对密封的流体域进行求解,以求得密封-转子系统的密封气流力,进而通过式(5)、式(6)计算得到不考虑涡动频率时,表征密封-转子系统稳定性的直接刚度与交叉耦合刚度系数。所使用的计算参数见表2。
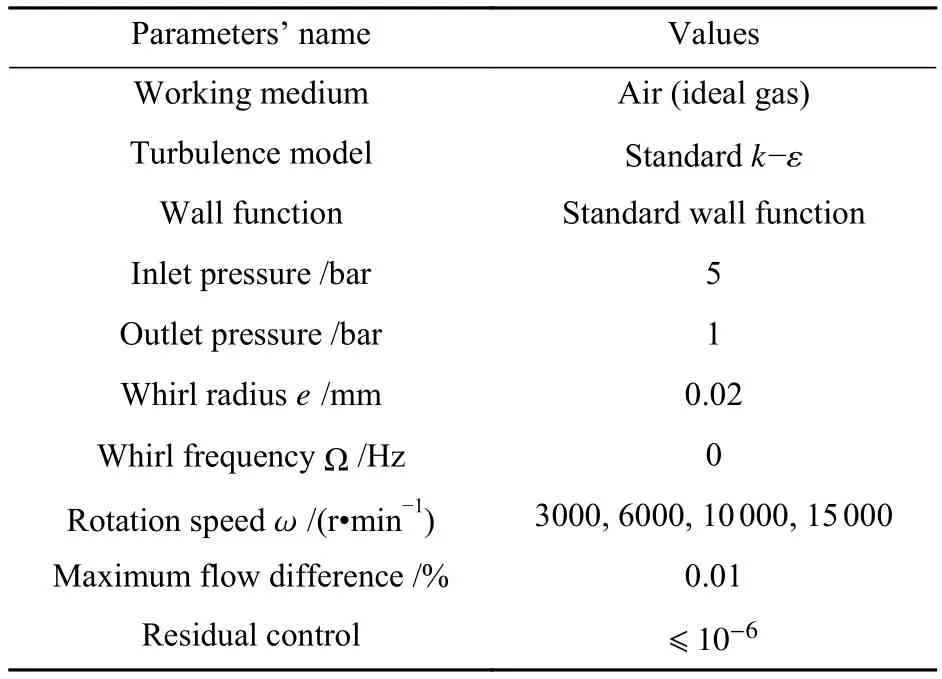
表2 计算工况Table 2 Calculation conditions
流体计算一般需要进行网格无关性验证,而由于类似的结构已在早先发表的论文中[24,26]进行了验证,且一般对于相似尺寸的密封求解也只需要不少于200万网格即可[22],故此处不再进行相关的网格无关性验证。图3a为传统迷宫密封的网格示意图,所划分的网格数为442万。而旋向槽-迷宫密封结构是在传统迷宫密封结构的基础之上设计得到,仅在旋向槽位置进行了额外的块划分与网格划分,故图3b仅展示旋向槽处的网格示意图。旋向槽-迷宫密封结构计算域所划分的总网格数为605万。
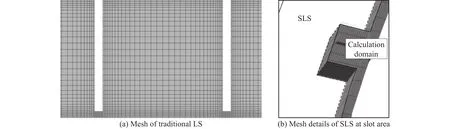
图3 传统直齿迷宫密封与旋向槽-迷宫密封网格示意图Fig.3 Grid diagram of traditional labyrinth seal and slot labyrinth seal
3 结果分析
3.1 两种密封结构对比
选取周向布置8个轴向偏转角为45°、微槽深度为0.2 mm、微槽宽度为0.8°的旋向槽-迷宫密封结构,并通过式(5)、式(6)计算出表征密封-转子系统稳定性的参数,即直接刚度系数与交叉耦合刚度系数。通过不同转速下2种密封结构的动力学特性和泄露性能的对比分析,对旋向槽-迷宫密封结构的设计思路进行验证。对比结果如图4所示。
由图4a可以发现,相较于传统迷宫密封,旋向槽-迷宫密封直接刚度系数在不同转速下的最大提升约为4.2%,且变化相对较稳定;从图4b中可以发现,交叉耦合刚度系数有33.4%的降低,且在较低的转速下具有负的交叉耦合刚度系数,能更大限度地提升系统稳定性。但由于前四级密封齿的开槽设计,导致密封齿对轴向流的节流效应出现了下降的趋势,反映为图4c中旋向槽-迷宫密封相较传统迷宫密封结构具有大约3.2%的泄漏量增值。
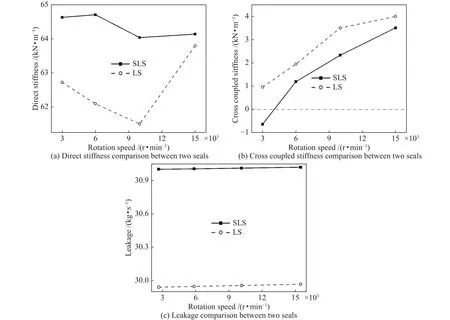
图4 不同转速下传统迷宫密封与旋向槽-迷宫密封结构的对比Fig.4 Comparison between traditional LS and SLS at different rotating speeds
由于旋向槽的提出是为了降低密封腔内的环流速度,且对于交叉耦合刚度系数的计算也获得了与之相匹配的结果,故进一步对两种密封结构的密封腔内和齿顶间隙区域的周向速度进行对比,结果如图5所示。

图5 不同位置传统迷宫密封与旋向槽-迷宫密封结构的切向速度对比Fig.5 Comparison of average circumferential velocity between traditional LS and SLS at different locations
从图5中可以发现:由于旋向槽的添加,不论是在齿顶处还是在腔室内,旋向槽-迷宫密封的平均周向速度均低于传统迷宫密封结构,甚至最大获得了44.47%、71.56%的降幅;其中所有4个密封腔室中的降幅比例持续增大,而齿顶间隙处的周向速度在最后一齿前也具有同样的变化规律;最后一齿由于并未设置旋向槽,故气流周向速度出现了回升,但依然相对传统迷宫密封有着31.85%的下降。
3.2 旋向槽-迷宫密封参数分析
在验证了旋向槽-迷宫密封结构相较传统迷宫密封结构,具有更优异的动力学特性的基础之上,按照表2所列不同结构参数进行了大量的仿真,得到了旋向槽不同参数对密封动力特性的影响规律如图6所示。
图6a反映了旋向槽宽度对动力特性的影响。可以发现,随着旋向槽宽度的增大,密封的直接刚度系数先增大后减小,上下波动在1 kN/m 范围内,影响较小;但同时交叉耦合刚度系数却从-0.6 kNs/m变为了正值,且在旋向槽宽度为0.8°时获得最大0.72 kNs/m的正值。由于交叉耦合刚度系数为正时会进一步降低转子系统的稳定性,直接刚度系数获得0.4%的提升并不能有效抵消交叉耦合刚度系数2.15倍的提升所带来有效阻尼系数[27]的降低,故较窄的旋向槽更利于提升系统的稳定性。图6b展示了密封动力系数随微槽数量变化的规律。随着微槽数量的增大,直接刚度系数出现了上下波动,其中,在周向8槽与16槽时获得了极大值,平均比0槽(对应传统迷宫密封结构)与12槽提升约3.3%;同时,交叉耦合刚度系数也出现了明显的下降,虽然在16槽时出现了一个回升,但在12槽处获得了最大1.39倍的降低。综合直接刚度系数与交叉耦合刚度系数,更多的旋向槽设计更有利于提升系统的稳定性。图6c绘制了密封动力系数随微槽深度的影响规律。可以发现,随着微槽深度的增大,直接刚度系数与交叉耦合刚度系数均朝着有利于提升转子稳定性的方向变化,并最终在0.6 mm处获得了6.0%的直接刚度提升与89.2%的交叉耦合刚度系数下降。更深的微槽会导致更多的气流出现周向速度的下降,从而提升稳定性,但是更大的开口却可能会带来更高的泄漏量。图6d则分析了微槽轴向偏转角度对密封动力特性的影响规律。随着轴向偏转角度的增大,直接刚度系数单调下降,但是交叉耦合刚度系数却出现了先增大后下降的趋势,且在30°、60°时交叉耦合刚度系数获得了基本一致的值;这是由于随着微槽轴向偏转角度的增大,上一级泄漏流在微槽处撞击微槽表面后会有更多的气流产生阻碍槽内射流的运动,导致参与抑制轴向环流的气流质量分数降低,最终导致了交叉耦合刚度系数的波动变化与直接刚度系数的持续降低。
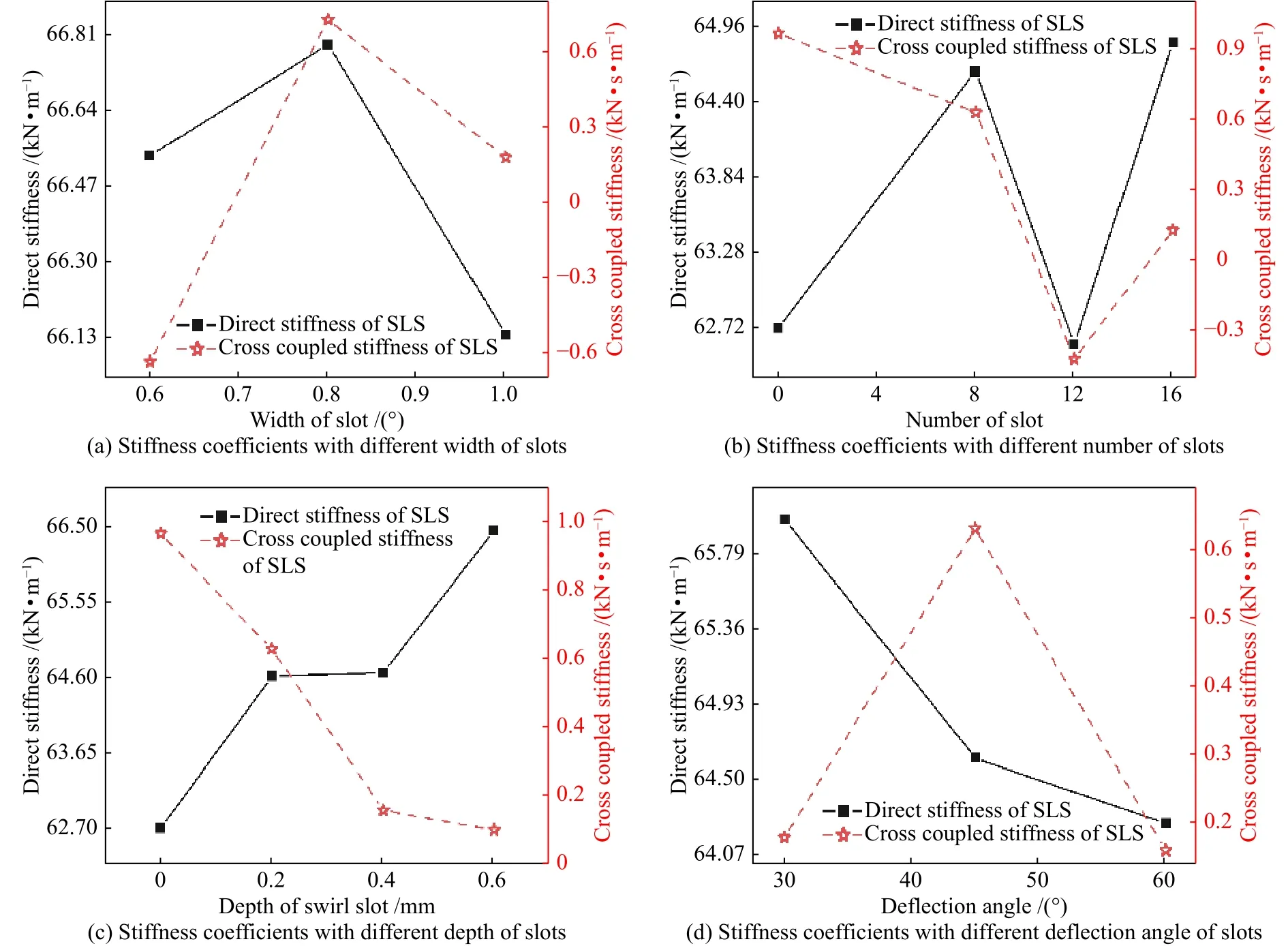
图6 旋向槽参数对密封动力特性的影响规律(转速3000 r/min)Fig.6 Influence of slot’s parameters on dynamic characteristics of SLS (with rotation speed 3000 r/min)
同时,将相应结构参数对泄漏量的影响规律绘制成如图7所示的曲线。
从图7中可以发现,旋向槽-迷宫密封结构参数对泄漏量的影响基本均为单调变化。除去上文提到的由于轴向偏转角度的增大导致通过微槽的流体质量降低所带来的泄漏量下降以外,增大旋向槽-迷宫密封结构的微槽宽度、微槽数量以及微槽深度都会一定程度的增大密封结构的泄漏量。

图7 旋向槽参数对泄漏量特性的影响规律(转速3000 r/min)Fig.7 Influence of slot’s parameters on leakage performance of SLS (with rotation speed 3000 r/min)
综合旋向槽结构参数对密封动力学系数以及泄漏量的影响规律可以得到:微槽宽度为0.6°、数量为16、深度为0.6 mm及轴向偏转角为60°时,能获得相对较好的稳定性能与相对较低的泄漏量性能。
4 结论
1)通过对传统迷宫密封齿的开槽设计,可大幅降低齿顶间隙及密封腔室内的工质环流速度,不同转速下的降低幅度可达44.47%、71.56%。

2)相对于传统直通齿迷宫密封结构,旋向槽-迷宫密封结构能获得约4.2%的直接刚度提升与33.4%的交叉耦合刚度降低,具有更好的动力学特性。但由于旋向槽处的分流,导致增加3.2%的泄漏量。
3)旋向槽宽度为 0.6°、数量为 16、深度为6 mm、轴向偏转角为60°时,能获得具有相对较好的稳定性能与较低泄漏量性能的旋向槽-迷宫密封结构。
