基于样本对选择的分层分类特征选择算法研究
2022-11-10折延宏武晋兰贺晓丽
折延宏,武晋兰,贺晓丽
(1.西安石油大学 理学院,陕西 西安 710000;2.西安石油大学 计算机学院,陕西 西安 710000)
0 引 言
大数据时代,数据的产生和收集速度急剧提升,样本数量、特征维度都在爆炸式增长,人们面临的分类学习任务也变得越发复杂,需要学习的类别数量迅速增加.另外,分类任务的规模还随着样本特征的维数疾速增加,给分类建模带来了新的挑战.标签的增加,及标签间可能会存在的语义结构,导致了结构化学习任务的产生.这种结构通常可以用层次树来表示,我们将这类任务称为分层分类.层次结构是分类学习的重要辅助信息,我们可以借助其挖掘到更多潜在有效信息.
特征选择的目的,是在保证分类准确性不发生降低的前提下,选择一个能够代表数据有效信息的特征子集.在高维度、大体量数据的分类任务中,特征选择可以降低算法时间复杂度,对后续处理步骤的运行时间和准确性都有重要影响.在特征选择中,一般会涉及实数型特征和离散型特征的处理.经典的粗糙集仅适用于离散型特征数据,模糊粗糙集作为描述条件属性和决策属性之间不一致性的有效数学工具,模糊粗糙集可以直接应用于数值或混合型数据.在模糊粗糙集模型中,可以通过定义模糊相似关系来度量样本之间的相似性,不再需要对数值属性值进行离散化,从而避免了重要信息的丢失,也就提高了分类精度.
在大规模数据的分类任务中,分层方法能够比平面分类技术产生更好的性能.Deng等[1]利用基于WordNet层次结构的类别距离度量方法推导了一个层次感知的分类代价函数.另外,由于类的层次结构提供了类的外部信息,一些研究侧重构建一个层次结构来处理大规模分类.Freeman等[2]将遗传算法融合到特征选择中,构造树状结构分类器.每个基本分类器都将数据集分割成一个越来越小的类集.为每个基分类器单独选择特征,同时进行树的设计和特征的选择.Jia等[3]设计了一种基于信息增益和特征频率分布的层次分类系统特征选择算法,以此得到具有较强判别性的特征子集,从而提高了分类效率和准确率.
近年来,模糊粗糙集理论在机器学习和模式识别领域中得到了广泛的关注,相关的应用研究也不少.Hu等[4]提出了一种信息测度来计算经典等价关系和模糊等价关系的识别能力,构造了基于该信息测度的两种贪婪降维算法,分别用于无监督和有监督数据降维.Jenson等[5]使用基于经典和模糊粗糙集的方法,设计了语义保持的降维方法.还有不少学者关注使用代表实例来进行特征选择.Zhang等[6]研究了基于模糊粗糙集的代表性实例的特征选择问题,对依赖函数进行了新的定义,并提出了有效的约简算法.次年该团队研究了将代表实例应用于基于模糊粗糙集的信息熵的增量特征选择,并在文献[7]中提出了主动增量特征选择算法.另外,Hu等[8]将高斯核与模糊粗糙集相结合,设计了一个基于核的模糊粗糙集模型,这是一种适用于大规模多模态的特征选择算法.对于分层分类的应用,Zhao等[9]设计了一种基于模糊粗糙集的分层分类的特征选择方法,利用类的层次结构关系构造模糊粗糙集模型,提出了基于兄弟节点的特征选择算法.后来,Zhao等[10]又提出了基于递归正则化的分层特征选择框架,将数据的分类拆分成多个子分类任务.但基于模糊粗糙集的分层分类方法研究仍然较少,鉴于模糊粗糙集对于描述不确定信息的优势,我们对其进行了更加深入的研究,并提出本文的分层分类方法.
本文提出了一种用于分层分类的模糊粗糙集模型,并开发了相应的特征选择算法.接下来的内容组织如下.在第1节中,给出了一些关于模糊粗糙集的预备知识,以及在分层分类中的相关作用.然后,在第2节中,提出层次辨识矩阵和样本对选择的概念,并给出了基于此的特征选择模型.在第3节引入了分层分类的评价指标.在第4节中,给出了实验结果并分析了分层特征选择算法的有效性.最后,在第5节,总结了本文并提出未来研究方向.
1 预备知识
1.1 模糊粗糙集属性约简
1.1.1 模糊粗糙集
(U,C,D)称为模糊决策系统,其中U为对象的集合,C是条件属性集,D是决策属性,其将样本划分为子集{d1,d2,…,dk}.
设U是一非空论域,R是U上一模糊二元关系,如果R满足以下:
1) 自反性:R(x,x)=1;
2) 对称性:R(x,y)=R(y,x);
3) 最小最大传递性:miny(R(x,y),R(y,z))≤R(x,z).
则称R为模糊等价关系.
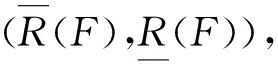
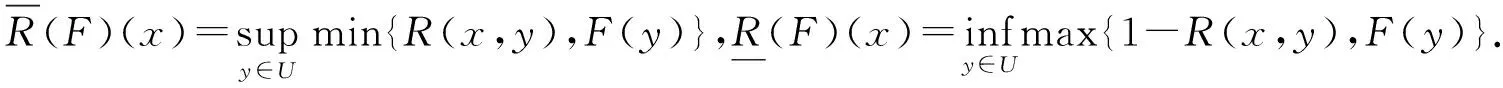
对于任意x∈U,如果R是一个模糊相似关系,D是经典决策属性,di是决策类,x对于di的隶属度定义为:
那么,模糊上、下近似分别为:
假设(U/D)={d1,d2,…,dk},D相对于C的正域定义为:
定义1[11]设(U,C∪D)为一个模糊决策系统,称子集P⊆C为C相对于D的一个约简,如果满足以下:
1)对于任意x∈U,PosP(D)(x)=PosC(D)(x);
2)对于任意a∈P,一定存在x∈U满足PosP-{a}(D)(x)=PosP(D)(x).
1.1.2 辨识矩阵[12]
设U={x1,x2,…,xn},如果cij是可以区分样本对(xi,xj)的可辨识性特征集,则MD(U,C)=(cij)n×n称为(U,C∪D)的辨识矩阵,其中元素cij的定义如下:
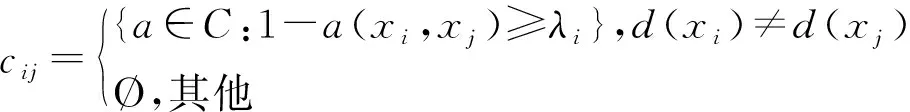
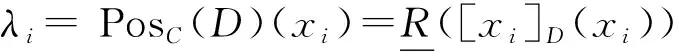
对于任意cij,如果在MD(U,C)中不存在另一个元素作为其子集,则称cij为MD(U,C)中的极小元素.
1.2 分层分类中的模糊粗糙集
1.2.1 分层分类
本论文针对的是基于树的层次类结构,其他结构暂不考虑.层次结构信息在决策类之间强加一种父子关系,这意味着属于特定类的实例也属于它的所有祖先类.分类通常可以形式化地表示为(D,),其中D是所有类的集合,“”表示从属关系,它是具有以下属性[13]的关系的子类:
1) 不对称性: 对于任意di,dj∈D,若didj,则不会有djdi.
2) 反自反性: 对于任意di∈D,都不会有didi.
3) 传递性: 对于di,dj,dk∈D,若有didj且djdk,那么一定有didk.
1.2.2 分层分类中的模糊粗糙集
经典模糊粗糙集的下近似在不同类别上的最小距离处取得,上近似在同一类别上的最大距离处取得.层次结构定义了类节点之间的从属关系,鉴于此,本文给出一种基于兄弟策略的模糊粗糙集模型,以进行特征选择以及分类.
基于树的层次结构可以表示为
定义2设(U,C,Dtree)为一个模糊决策系统,若R是一个模糊相似关系,Dtree是满足从属关系的经典决策属性,对于任意x∈U,兄弟策略下近似定义为:
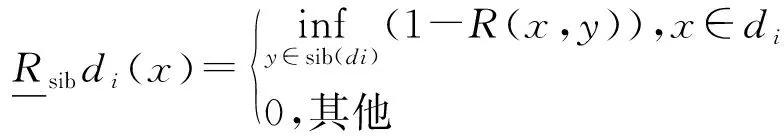
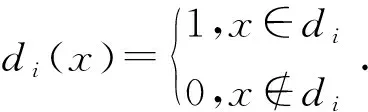
与经典模糊粗糙集中下近似的定义相比,我们有以下结论[9]:
命题1已知
命题2已知
2 分层特征选择
传统的特征选择算法假定所有的类别是相互独立的,部分学者借助类层次结构将复杂的问题分而治之,没有将层次结构信息融合到特征选择任务中.粗糙集理论可以有效地利用条件属性与决策类之间的相关性来进行特征选择.本文将叶节点设为实际类,采用上一节中的兄弟策略下近似来进行特征选择.
2.1 层次辨识矩阵
定义3给定一个分层分类问题
如果a∈C满足PosC-{a}(Dtree)=PosC(Dtree),则称a在C中相对于Dtree不必要,否则称a在C中相对于Dtree必要.对于P⊆C,如果有PosP(Dtree)=PosC(Dtree),且P中任何一个条件属性在P中相对于Dtree都必要,则称P是C的相对于Dtree的属性约简.C中相对于Dtree的全部必要条件属性集合称为C相对于Dtree的核心,记为CoreDtree(C).如果用RedDtree(C)表示C相对于Dtree的全部属性约简集合,易证CoreDtree(C)=∩RedDtree(C).
定义4对于一个分层分类问题
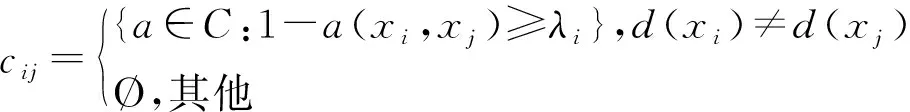
式中:λi=PosB(Dtree)(xi).
布尔函数fU(C∪Dtree)=∧(∨cij),cij≠Ø,是决策系统(U,C∪Dtree)的辨识函数,其中∨(cij)是所有满足a∈cij的变量的析取.设gU(C∪Dtree)是fU(C∪Dtree)通过尽可能多的分配律和吸收律得到的最小析取形式,则存在t和Bi∈C,i=1,2,…,t,使得gU(C∪Dtree)=(∧B1)∨… ∨(∧Bt),其中Bt中每个元素只出现一次.
定理1:假设P⊆C,那么P包含C的一个相对约简,当且仅当对于任意cij≠Ø有P∩cij≠Ø成立.
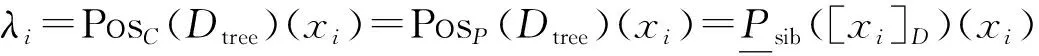
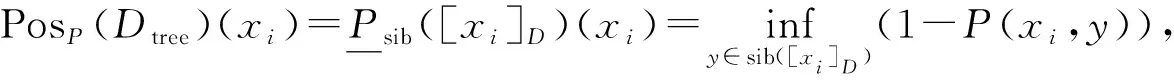
2.2 寻找约简
在本节中,首先用一个例子说明行文的动机.然后利用条件属性的相对辨识关系来刻画层次辨识矩阵中的极小元素.最后,设计了一个算法找到属性约简集.
例:假设U={x1,x2,…,x7},C={c1,c2,c3,c4},R={R1,R2,R3,R4}是由四个条件属性导出的模糊相似关系,Dtree={d0,A,B},d0是根节点,A和B是d0的直接子类.U被决策属性划分为{A,B},A={x1,x2,x5},B={x3,x4,x6,x7}.对于模糊决策系统(U,C∪Dtree),由条件属性导出的模糊相似关系及由整个条件属性集导出的模糊相似关系R为:
根据层次辨识矩阵的定义有:
由极小元素的定义可知,{2},{1,4}以及{3,4}是层次辨识矩阵的所有极小元素.辨识函数通过吸收律可以简化为fU(C∪Dtree)=(R2)∧(R1∨R4)∧(R3∨R4).如果我们可以在计算整个层次辨识矩阵之前得到这些极小元素,那么寻找约简的搜索范围就会得到压缩,计算复杂度也会大大降低.现在关键问题是如何不计算整个层次辨识矩阵就能得到极小元素,接下来的理论可以为解决这个问题提供支撑.
定义5对于一个分层分类问题
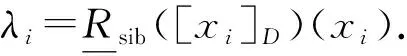
DIS(C)=∩a∈CDIS(a).显然,(xi,xj)∈DIS(a)⟺若cij≠Ø则有a∈cij.
定义6[15]Sij=∩{DIS(a):(xi,xj)∈DIS(a)}.
对于(xi,xj)∈DIS(C),一定存在a∈C满足(xi,xj)∈DIS(a),那么一定存在Sij满足(xi,xj)∈Sij,所以有∪Sij=DIS(C).
这里我们明确极大样本对集的定义:对于任意Sst≠Sij,都有Sij⊄Sst,则称Sij是极大的.
推论1从DIS(C)中删除DIS(a),会删除所有满足a∈cij的Sij.
定义7Nij=|{a:(xi,xj)∈DIS(a)}|.
Nij是满足(xi,xj)∈DIS(a)的条件属性a的个数,容易看出Nij=|cij|.
对于Sij,Nij和cij,有下面的定理:
定理2.1对于任意(xs,xt)∈Sij,(xs,xt)≠(xi,xj),有Sij⊇Sst和Nst≥Nij.
证明:(xs,xt)∈Sij,Sij=∩{DIS(a):(xi,xj)∈DIS(a)}=∩{DIS(a):a∈cij},那么能区分(xi,xj)的属性也能够区分(xs,xt),但也存在其他属性能够区分(xs,xt),因此有cij⊇cst.故由Sij定义知Sij⊇Sst,由Nij定义知Nij≤Nst.
定理2.2对于两个极小元素cij和cst,有(xi,xj)∉Sst和(xs,xt)∉Sij.
证明:对于两个极小元素cij≠cst,存在P∈cij,Q∈cst,但又P∉cst,Q∉cij.即(xi,xj)∉(DIS(Q),(xs,xt)∉(DIS(P),由Sij的定义知(xi,xj)Sst,(xs,xt)Sij.
定理2.3当且仅当Sij是极大的,cij是MDtree(U,C)中的极小元素.
证明:“⟸”:若cij是极小元素,由极小元素定义,对任意cst≠cij,都有cst⊄cij.即存在a∈cst,a∉cij,则(xs,xt)∈DIS(a),(xi,xj)∉(DIS(a).根据Sst的定义及集合间的包含关系有(xi,xj)∉Sst.又对于任意Sst≠Sij,一定有(xi,xj)∈Sij,由此能够推出Sij⊄Sst,故Sij是极大的.
“⟹”:已知Sij是极大的,要证cij是极小元素,即对于任意cst≠cij,存在a∈cst且a∉cij.若cst≠cij,那么cst⊂cij或cst⊄cij.根据Sij的定义,cst⊂cij,由此可推出Sij⊆Sst,然而,这与Sij是极大的相矛盾,故cst⊄cij,即存在a∈cst且a∉cij.
推论2从DIS(C)中删除极小元素cij对应的极大样本对集Sij可以删除所有的Sst⊆Sij,但不会完全删除其他极小元素cst对应的Sst.
推论3Nij最小的样本对(xi,xj)对应一个极小元素cij.
定理2.4∪{Sij:cij是极小元素}=DIS(C).
证明:左边⊆右边显然成立.下证右边⊆左边:对于任意(xs,xt)∈DIS(C),有(xs,xt)∈Sst.由于极大样本对集对应极小元素,当存在极大Sij使得Sst⊆Sij时,有(xs,xt)∈Sij,这时cij是极小元素.若不存在,那么Sst就是极大样本对集,cst是极小元素.故对任意(xs,xt)∈DIS(C),有(xs,xt)∈∪{Sij:cij是极小元素}.
推论4当且仅当DIS(C)=Ø时,所有极小元素cij对应的Sij都从DIS(C)中被删除.
根据以上定理和推论,通过对DIS(C)中的样本对(xi,xj)升序排序,可以从DIS(C)中依次删除最小Nij对应的Sij,直到DIS(C)=Ø,这样可以得到MDtree(U,C)中所有极小元素的集合.进而通过辨识函数,可以找到所有约简.但实际上我们只需要一个约简,即找到辨识函数的最小析取形式中的一个合取范式.我们只需选择辨识函数中的一个元素a∈cij,而忽略辨识函数中其他包含a的元素,这与我们由辨识函数化为其简化形式的思路一致.
结合极小元素的这些性质,我们设计以下算法来得到条件属性集的一个约简:

算法:基于样本对选择的分层特征选择算法(HierSPS-FS) 输入:U,C,Dtree输出:特征子集REDUCT1 初始化REDUCT为空集;2 计算每个特征的相对辨识关系DIS(a),DIS(C)和Nij;3 while(DIS(C)≠Ø) do4 找到DIS(C)中的最小值Ni0j0对应的(xi0,xj0);5 for(a∈C) do6 if((xi0,xj0)∈DIS(a)) then7 if(a∉REDUCT) then8 向子集REDUCT中追加特征;9 更新DIS(C)=DIS(C)-DIS(a);10 end if11 将Ni0j0设为inf;12 end if13 end for14 end while15 返回约简集REDUCT;
在特征选择算法中,我们首先计算每个特征的层次相对辨识关系,然后计算原始特征集的层次相对辨识关系,以及每个样本对能够被多少特征区分.在接下来的循环中,我们根据Nij的大小对样本对进行排序,找到Nij值最小的样本对.然后遍历整个特征集,找到能够区分该样本对的特征并加入约简集.这里我们只要找到一个能够区分该样本对的特征就退出该次循环,去寻找下一个关键的样本对,因此节约了将冗余特征加入约简集的时间,但又保证约简集的辨识能力.
3 评价方法
传统的多分类任务指标,例如F1度量能够反映分类器对于不同类别的分类能力,但是它在分层结构中无法准确地描述错分的程度.图1是动物的类别层次结构,绿色方框表示某个样本的真实标签,黄色方框表示两个分类器的预测标签.假设该样本的真实标签是猫,一个分类器将其预测为老虎,另一个分类器将其预测为青蛙,那么这两种错误的程度是不同的,但传统分类评价标准无法实现这种对于错误程度的区分,故需要一些基于层次结构的分层分类评价指标.
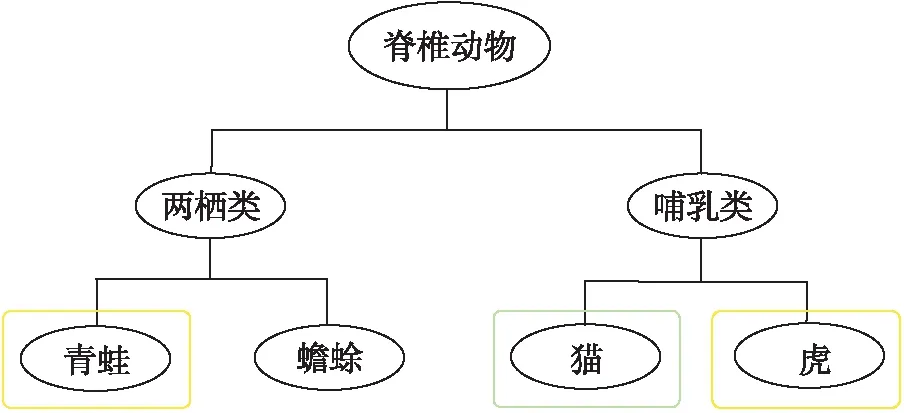
图1 动物的类别层次Fig.1 Categorical irony level of animals
3.1 树诱导损失
3.2 分层F1测度
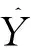
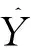
分层F1测度的定义为:
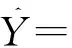
3.3 最近公共祖先(LCA) F1测度
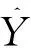
4 实验分析
在本节中,首先介绍我们实验中使用的两个数据集.然后,将提出的分层特征选择与[17]中提出的平面特征选择进行比较.所有数值实验均在MATLAB R2018b中实现,并在运行速度为 3.00 GHz、内存为 16.0 GB,64位Windows 10操作系统的Intel Core i7-9700上执行.在训练集上选择特征子集,并分别使用SVM、KNN和NB分类器在测试集上进行测试.对于SVM分类器,使用线性核和c=1进行十次交叉验证.对于KNN分类器,在初步实验的基础上为类决策设置了参数k=5.
4.1 数据集
实验使用了三个数据集,表1提供了这些数据集的基本统计数据.

表1 数据集基本信息
第一个数据集是来自加州大学欧文分校提出的用于机器学习的数据库UCI中的Bridges[18],它一般用于分类,是一个小型的数据集,只有108个样本.
第二个数据集是DD数据集[19],它是一个蛋白质数据集.它有 3 625 个样本和473个特征.它有27个实类和4个主要结构类.
第三个数据集F194也是一个蛋白质数据集[20],它有 8 525 个样本和473个特征.此数据集中有194个类,都是叶节点.
最后一个SAIAPR[21],是图像相关的数据集,每个图像都经过手动分割并根据预定义的标签词汇表对结果进行标注;词汇是按照语义概念的层次结构组织的.根据文献[22],物体可以分为六个主要分支:“动物”、“景观”、“人造的”、“人类”、“食物”或“其他”.
4.2 实验步骤
为了评估文中的分层特征选择算法的性能,进行了一些对比实验.具体的实验研究安排如下:
1) 基线对比:将选择所有原始特征和进行特征选择后实验情况对比.文中的基于样本对选择的分层特征选择算法记为HierSPS-FS.
2) 使用分层评价指标进行比较:将所提出的算法与平面特征选择算法进行了比较.这里采用的平面特征选择算法也是基于模糊粗糙集的特征选择算法,CHEN等[16]定义了条件属性的相对辨识关系,用相对辨识关系来表征模糊辨识矩阵中的极小元素,进而提出了一个基于模糊粗糙集的约简算法这里记为FlatSPS-FS.
3) 将提出的算法与其他两种分层方法进行比较.文献[9]中的HierDep-FS也是一种基于模糊粗糙集的分层分类算法,其本质是根据模糊近似空间中下近似以及特征的依赖函数,最后得到能够代表整个特征空间的约简集.该论文的作者还在文献[10]中研究了一种基于正则项的特征选择方法HiRR-FS,该方法是一种局部约简方法,为每个子分类器选择不同的约简集.
4.3 实验结果分析
在以下几方面来评估所提出的特征选择算法的性能.
1) 与基线方法的比较(选择所有特征)
文中的算法是针对具有层次关系的大规模数据集而设计的,因此可能会出现特征量成百上千,甚至更多的情况,但数据具有判别性的特征,事实上只占很小一部分.如果直接对原数据进行训练,那么其他无关特征可能会影响分类准确率.其次,特征量和样本量都是影响运行时间的重要因素,巨大的特征量使模型训练需要更长的时间,几个小时甚至几天.图2是本文使用的四个数据集在进行特征选择和直接用原特征集进行分类的时间对比,由于Bridges数据集的样本量和特征数量均较小,运行时间对比并不明显,但根据其他几个较大数据集的实验数据仍可以明显看出,本文所提出的特征选择算法对分类运行时间的压缩效果.
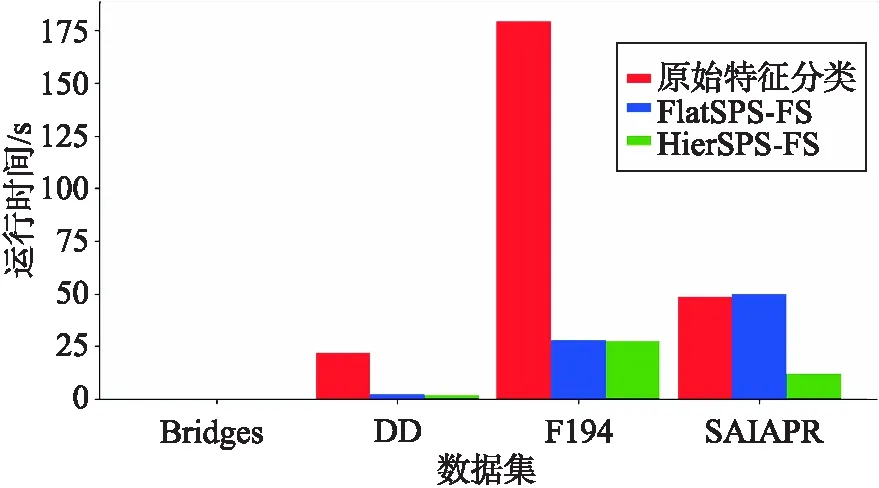
图2 运行时间对比Fig.2 Comparison of runtime
接下来,在表2中列出的数据集上,直观地比较所提出算法与平面算法以及不进行特征选择的分类精度.每项指标的最佳表现都以粗体突出显示.可以观察到,通过分层方法选择的特征的性能优于平面方法.

表2 基线算法、平面特征选择算法和分层特征选择算法在不同数据集上的分类准确率
2) 使用分层评价指标进行比较
在平面分类问题中,通常使用SVM、KNN和NB等算法来测试分类精度.在层次分类问题中,文中仍然使用这三种最常见的分类器,但由于层次分类的输出只是类层次结构的一部分,因此使用的评价指标有所调整.在上一节中,详细分析了平面分类和分层分类的特点,并引入了分层分类的评价指标.因此,我们接下来使用分层评价指标来评估本文算法的性能.表3中,我们使用不同的分类器来测试不同的数据集上的树诱导损失以及基于最近公共祖先的F1测度,可以直观地比较所提出算法在3种分类器下的效果.可以观察到,在SVM上使用分层方法选择的特征的分类准确度更高.
树诱导损失TIE可以体现由层次结构引起的一些不同程度的错误,TIE之后的“↓”表示该值“越小越好”;Hierarchical-F1和LCA-F1是基于集合的度量,能够平衡分层精确度和召回率,其后的“↑”表示该值“越大越好”.在表3中描述了在3个数据集上分层评价指标的结果.可以看出,分层特征选择比平面特征选择具有更好的性能.

表3 不同数据集上的分层评价指标
关于表3中的三项评估度量,有以下发现:
(1) TIE的值与数据集中决策类的层次结构的规模有较大关系.
(2) 对于任意一个数据集来说,F_LCA的值都小于F_Hierarchical的值.这是因为有许多共同的祖先往往会使错误变得过于严重.LCA-F1可以避免此类错误.
(3) 与其他分层方法进行比较
表4列出了不同数据集上不同特征选择算法的分层F1度量结果.对于分层F1度量,越高越好.

表4 不同分层方法的Hierarchical_F1测度比较
5 结 论
为了加快大规模数据集的分类速度,以及更好地评估具有层次结构数据集的分类准确度,本文提出了一种基于样本对选择的分层分类特征选择算法.基于大规模数据集复杂的数据结构,使用兄弟节点的样本作为负样本集来计算模糊下近似值,提出了一种考虑兄弟策略的层次辨识矩阵,并引入了新的相对辨识关系,最后通过一些严谨且巧妙的方法找到约简.
该算法目前仅考虑了决策类标签的树结构,事实上还有一些其他复杂的结构,比如有向无环图和链结构等.在未来的研究工作中,将讨论这类任务的特征选择算法.此外,该算法仅从原始特征集合中选择一些判别行特征,对层次关系的利用不够充分.可以扩展模糊粗糙集的优势,根据类标签结构,为每一个子分类任务选择一个约简子集.未来将设计相关用于分层特征选择的模型和算法.
