基于几何一致性加权的二部图点云配准方法

夏坎强

(上海理工大学机械工程学院，上海 200093)

0 引言

近年来，随着3D 采集技术的迅猛发展，三维传感器逐渐从实验室走进了大众的视野，例如各种类型的3D 扫描仪、激光雷达与RGB-D 相机。与2D 图像相比，三维数据可以表达更加丰富的几何、形状等信息并能够以更好的视角描绘物体整体面貌。点云配准是将具有重叠部分、在不同视角下采集到的点云，通过变换矩阵的转化，统一到同一坐标系的算法。点云配准在不同领域有很多应用，如三维重建[1]、三维定位[2]与姿态估计[3]等。

传统的点云配准算法是由Besl 等[4]提出的迭代最近点(ICP)算法，该算法采用点对点的距离度量，通过迭代的方式最小化两点云对应点间的欧式距离解决配准问题。李绕波[5]等提出一种基于对偶四元素描述的配准方法，利用线面的几何约束关系构建空间变换函数并利用最小二乘法计算变换矩阵，该方法对面特征较少的点云效果不佳。Segal[6]等提出一种广义的ICP，允许点到点和点到面变量中包含任意协方差矩阵，其基本思想是将点云看作一个采样的二维流形，用局部表面法线来表示点云。王珊[7]等提出一种基于特征点的匹配算法，对特征点使用双向最近邻距离比匹配并根据不同点云设置收敛阈值，但算法对收敛阈值较为敏感。李新春[8]等提出一种基于邻域特征点提取与匹配的配准方法，提高了特征点的分辨率，但该算法配准时间较长。陈强[9]等提出一种基于特征空间匹配的点云配准算法，利用PointNet 模型提取特征空间，通过RANSAC 与ICP 完成粗配准与精配准，但该算法设计参数较多，配准流程较繁琐。张旭春等[10]提出一种基于多尺度集距离约束的配准方法，通过在FPFH 算法提取不同尺度下的特征点并结合距离约束条件完成点云配准，但该算法运行速度较慢。

本文提出一种基于图的优化配准方法，实现了对点云中错误对应关系的筛除以及变换矩阵的求解。结合点云对应点对的几何一致性，在几何空间与特征描述符的复合空间上度量特征点对的相似性。同时，从特征点对全局配准的角度出发，将点云配准问题转化为二部图的匹配任务并应用Kuhn-Munkres(KM)[11]算法求解正确的对应关系，最后通过SVD 分解计算变换矩阵。

1 方法原理

1.1 方法框架

本文算法流程如图1 所示。首先，利用内部形状描述子(ISS)算法检测待配准点云特征点并计算其3DSC 特征描述符以编码特征点局部信息。同时，利用快速点对特征直方图(FPFH)构建点云初始候选对应点对并利用几何空间一致性确定置信度较高的基准点对，以此计算后续匹配点对的几何一致性系数。接着，将点云对应点匹配任务描述为一个代价函数，它在3DSC 特征和欧式几何空间上对特征点的全局相似性进行建模，然后，利用KM 算法优化全局代价函数用以确定特征点对应关系，最后，利用奇异值分解(SVD)估计最优变换，实现点云配准。

图1 算法流程图

1.2 几何空间一致性系数

传统特征点对使用欧氏距离确立对应关系，不仅忽略了3D刚性变换的独特性，而且会在配准中带来错误的匹配。由图2 中可知，基础对应点对间的距离是固定的，但错误匹配点对P3与Q3间的距离与基础匹配点对(P1,Q1)的距离相同。故单纯依靠两点云间的欧氏距离会给匹配带来歧义，进而影响最终的匹配效果。几何空间一致性则是利用点云自身特征点间的距离恒定(如P1P2)，其在经过变换后仍满足自身特征点对距离恒定的特点(如Q1Q2)。

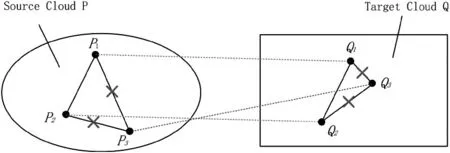
图2 几何空间一致性示意图

几何空间一致性加权依赖于匹配点云的预对应假设，本文选用快速特征点直方图(FPFH)描述子进行预匹配点云匹配对(p,q)，然后通过几何空间一致性筛选候选正确对应点对，如图2 所示。当两组匹配点对(p1,q1),(p2,q2)满足式(1)时，将其列为候选匹配点对。式⑴中，p1,p2表示源点云中的特征点，q1,q2是目标点云中的特征点。‖ * ‖2表示向量2范数。

对于三维空间而言，满足式⑴的候选匹配点对可能会有歧义性，因此需要统计满足公式的对应点对的次数。由于正确的匹配对在计算过程中会被多次使用形成稳定的多边形共面几何结构，所以当统计计数大于计数阈值时，将其定义为基础对应点对。

通过计算待匹配点对(pi,qj)与置信度较高的基础对应点对(pt,qt)之间的几何一致性，可以得到该对匹配点的内在几何一致性度量。具体来说，通过测量源点云中的特征点与基准点的距离与其在目标点云对应的点对距离的均值差来计算几何空间相关性gpq，如式⑵。

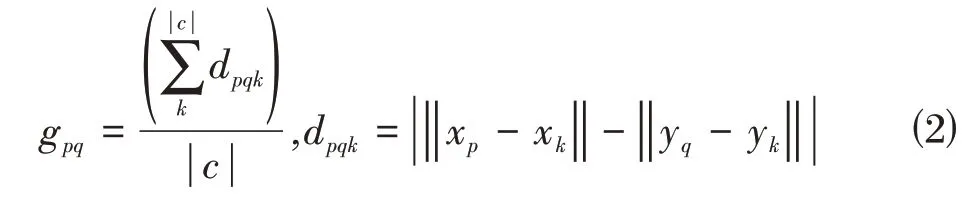
其中，gpq表示点云匹配对(p,q)的几何空间相关性，|c|是基准对应点对的个数，(xk,yk)是源点云与目标点云的基础对应点对，dpqk是源点云中的点对(xk,yk)与目标点云中的点对(yp,yk)的长度差。

由于几何相关性与3DSC 的特征描述符量纲不一致，本文选用威尔式公式将特征点p与q的几何相关度量映射至0-1 区间以此对特征点3DSC 描述符欧氏距离进行加权表示，几何一致性系数ψγ(p,q)如式⑶。其中，ψγ(p,q)表示点云匹配对(p,q)的几何一致性系数，γ代表威尔式公式核宽。

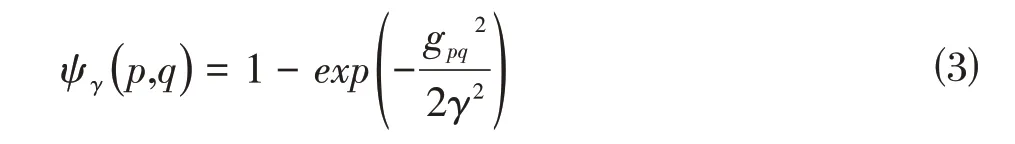
1.3 代价函数构建

从点云特征点对的整体对应关系出发，构造了一个用于特征点匹配的全局代价函数Ecos t来表征对应点匹配的正确性，该函数主要由匹配代价与惩罚代价组成，如式⑷。匹配代价表征源点云与目标点云对应关键点相似性度量，而惩罚代价表征未匹配点对的数量。

对于匹配代价LMatch_cos t，其由特征点描述符欧式距离与几何空间一致性加权和构成，如式⑸所示。

其中，M是两点云的对应匹配集。ED3dsc(p,q)表示匹配点对(p,q)的3DSC 描述符欧氏距离。惩罚代价LPenalty_cos t由未匹配点个数以及惩罚权重表示，|φ|是未匹配特征点个数，Wp是惩罚权重，如式⑹。通过最小化代价函数Ecos t，可以得到匹配集{M,φ}*，如式⑺。

1.4 基于KM算法的代价函数优化

寻找源点云与目标点云特征点对的正确对应关系可以建模为二部图的最优匹配问题。在加权二部图G=(S,T,E)中，两个不相交的点集结点视为源点云S与目标点云T的特征点，结点间的权值大小E可以由特征点描述符欧式距离与几何空间一致性加权表征。KM算法的求解需要满足两点集结点个数一致，故假设源点云中与目标点云中分别检测到m与n个特征点，在特征点个数m与n不一致时，需要添加|m-n| 个虚拟节点Nv来满足算法的运行。每条边e(p,q) 的大小表示源点云S中的p特征点与目标点云T中的q特征点的复合距离即几何一致性加权的3DSC 欧式距离。为防止异常值对算法的影响，设置未匹配点对阈值Tcd，Tcd的计算公式如式⑻。通过计算源点云S与目标点云T中所有特征点对的匹配矩阵Mcd的均值μcd与标准差σcd来获得Tcd，t设置为1。确定未匹配点对阈值Tcd后，对应边权值e(p,q)计算如下：

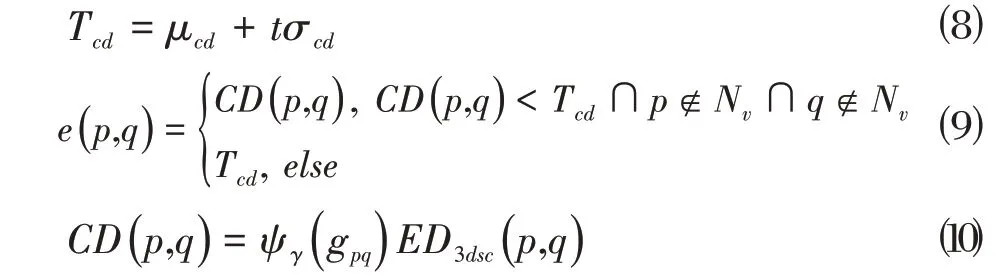
当Tcd=2Wp时，所有边的最小权值和与代价函数相差常数值，如式⑾。因此，代价函数最小值的求解可以通过加权二部图的KM 算法得出。其中，被选中边的权重e*(p,q)＜Tcd最终构成源点云与目标点云的对应匹配集合M*，同时未匹配点集φ*也被确定。图3 展示了KM 算法求解过程的简单示例，其中Mgd表示所有特征点对的几何一致性系数矩阵；M3dsc表示所有特征点对的3DSC 特征描述符欧式距离矩阵；Mbg表示特征点对的二部图矩阵，图3(c)中的绿线连接即为求解的对应特征点对。

图3 K-M算法示意图

以上证明了在给定一个点云对和一个固定阈值的情况下,可以通过求解来计算。给定如上所述的加权二部图G=(S,T,E)，采用KM 算法将寻找最小权重匹配的优化问题转化为寻找点云匹配中对应特征点的匹配问题，输出点云特征点的对应关系。一旦确定对应关系，就可以通过奇异值分解(SVD)来计算变换矩阵，如式⑿。

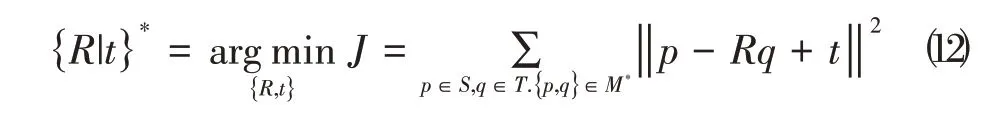
2 实验结果与分析

实验为：实际点云的算法配准实验。

为验证配准算法在实际场景中的配准效果，使用RealSense 设备采集零件点云，并应用该算法进行点云配准。如图4 所示。本文共采集三个零件点云，对实际工件点云应用本文算法时，将原始工件点云与目标工件点云的ISS 特征点检测算法的球邻域半径设置为0.01，非极大抑制半径设置为0.01。为直观地显示配准算法对实际场景中的工件的配准效果，对配准过程进行可视化显示。图4(a)显示了零件点云的初始位姿；图4(b)显示了点云经过粗配准后的结果，从工件在粗配准中的位姿关系可以看出两者已经处于较近的距离，工件场景点云与模板点云已经建立正确的位姿关系，表明算法较好地完成了粗配准的任务。为进一步细化两点云之间的位姿差异，利用ICP 精配准算法对上述模型进行优化迭代。对工件点云模型的最终配准效果如图4(c)所示，可以看到工件原始点云与工件目标点云基本准确配准。

图4 零件点云配准图

为验证本文算法在粗配准阶段的运算时间与精度优势，将该算法与“基于SAC-IA 与ICP 的点云配准算法[12]”和“利用特征点采样一致性改进ICP 算法点云配准方法[13]”的粗配准部分进行对比。分别采用工件a、工件b 和工件c 的原始点云，以及目标点云，点云配准误差由均方根误差表征。对三种不同的配准方法进行比较，其实验结果可视化如图5 所示。实验结果用表1表示不同算法对零件粗配准的精度；用表2表示不同算法对零件的粗配准时间。

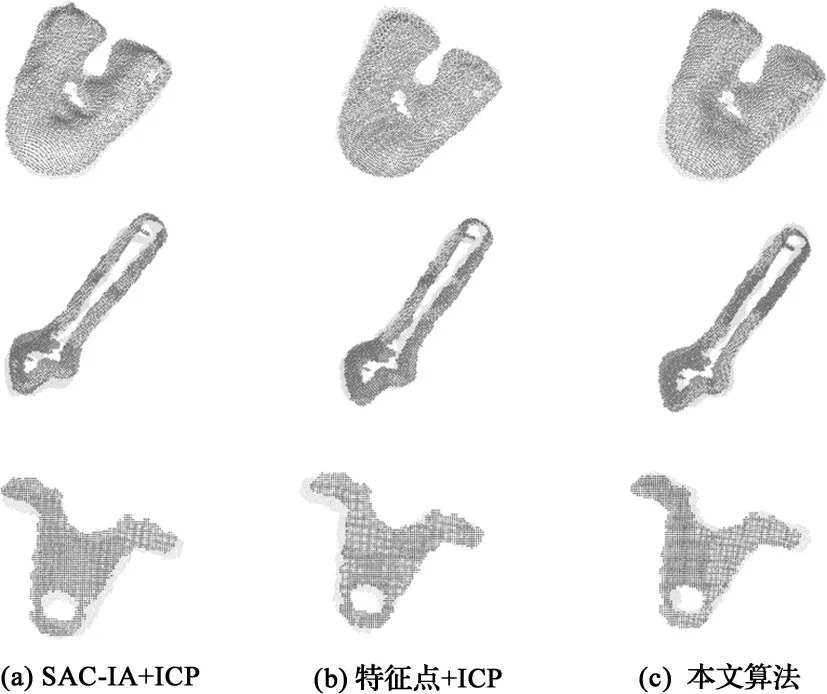
图5 不同算法工件点云粗配准图

表1 不同算法对零件的粗配准精度(mm)

表2 不同算法对零件的粗配准时间(s)

3 结论

针对传统点云配准ICP需要两点云具有相对良好的初始位姿，否则算法容易陷入局部最优而导致配准失败的问题。本文从特征点对全局匹配的思路出发，将对应点对匹配与二部图完备匹配相结合。通过引入几何一致性赋权的特征点对3DSC 描述符欧氏距离来定义二部图的权值矩阵，利用二部图匹配的KM 算法得出特征点对的对应关系并应用SVD 分解完成点云粗配准。所提算法为精配准ICP 提供优化后的位姿，提高了精配准的ICP的精度。实验结果表明，与传统配准方法相比，来算法在保证精度的情况下，提高了点云粗配准的速度。但仍需注意的是，该配准算法对点云质量有一定要求，重叠率较低的点云由于缺少足够的关键特征点会影响算法的最终匹配效果，进而对精配准带来误差。