关注统计概念形成提升学生思维能力

刘秀妹 孙道斌

新课程实施以来，教师的教学理念得到了更新和转变，但是，在一些统计课教学中，“突出统计运算，淡化统计意识的形成”的现象仍然普遍存在，大多数教师会直接给出概念或公式，然后让学生通过反复的训练来强化记忆相关的公式和概念，硬是将学生知识的获得建立在“灌输和操练”的基础之上了．这些做法实际上是将隶属于“统计”的概念连同公式一起混同在“数与代数”课程领域之中了，它与《义务教育数学课程标准（2011年版）》（以下简称《标准（2011年版）》）对该主题的学习定位是相悖的，《标准（2011年版）》明确将“数据分析观念”作为核心概念之一[1]，也就是说，在初中阶段学生学习“统计”的核心目标就是发展“数据分析观念”，因此，学习时一定要让学生经历统计工作的完整过程，尽量淡化课程设计中的统计运算，突出统计意识的形成[2]．基于以上的理解和思考，笔者对“6.4数据的离散程度（1）”（北师大版《义务教育教科书·数学》八年级上册）教学进行了有益的探索和新的尝试，旨在让学生知道为什么要学习方差，方差计算程序是怎么来的，进而揭示方差的本质，让学生经历方差概念学习的形成过程，提升学生的数据分析观念和思维能力，现将这节课的教学设计呈现如下，并解读立意，以供研讨．

1 教学设计

1.1设置情境，引发冲突

师：在统计学中，平均数、中位数、众数是用来描述数据集中趋势的三个特征量，除此之外，还有一类用来刻画数据波动（离散）程度的特征量．本节课，我们将在新的实际问题情境中，来了解这类“特征量”的统计意义并用其解决实际问题．

问题1为了提高农副产品的国际竞争力，一些行业协会对农副产品的规格进行了划分，某外贸公司要出口一批规格为759的鸡腿，现有2个厂家提供货源，它们的价格相同，鸡腿的品质也相近．

质检员分别从甲、乙两厂的产品中抽样调查了20只鸡腿，它们的质量（单位：g）如下：

甲厂：75， 74， 74， 76， 73， 76， 75， 77， 77，74， 74， 75， 75， 76， 73， 76， 73， 78， 77， 72;

乙厂：75， 78， 72， 77， 74， 75， 73， 79， 72，75， 80， 71， 76， 77， 73， 78， 71， 76， 73， 75.

把这些数据表示成下图：

如果只考虑鸡腿的规格，根据这些数据你认为外贸公司应购买哪家公司的鸡腿？说明你的理由，

追问1：外贸公司购买哪家公司的鸡腿，可用什么量来描述？请计算后说明？

师生活动：受前面知识及思维习惯的影响，学生容易用平均数描述．教师引导学生思考、阐明自己的看法，学生很快计算出甲、乙两厂产品的平均质量（平均数）分别是x甲= 75g；x乙=75 g．教师引导学生画出表示平均质量的直线，如图2．

追问2：这个结果说明了什么？

师生活动：学生很容易得出甲、乙两厂产品的平均质量相同，都与规定的规格相同，教师引导学生继续思考，学生意识到，用平均数不能解决问题．

追问3：既然甲、乙两厂产品的平均质量都与规定的规格相同，换言之，仅凭“平均数”这个统计特征量不能解决问题．看来要确定外贸公司会购买哪家公司的鸡腿，得采用新“衡量标准”重新选择，那么用来描述这个“衡量标准”的量又是什么呢？

师生活动：学生积极思考．教师顺势引导，平均数描述的是一组数据的集中程度，由图2可以看出，甲、乙两厂的数据分布情况并不能用平均数来解释，它们是分散在“质量平均线”上下方的，像大大小小的波浪，波峰和波谷大小不一，这就是数据的波动性．引出追问4．

迫问4：从甲厂抽取的这20只鸡腿质量的最大值是多少？最小值又是多少？它们相差几克？从乙厂抽取的这20只鸡腿质量的最大值又是多少？最小值呢？它们相差几克？

师生活动：在学生讨论交流的基础上，教师结合实例给出极差的概念：极差是指一组数据中最大数据与最小数据的差．说明它是刻画数据离散程度（波动性）的一个统计量．

追问5：这是不是说甲、乙两厂产品的质量一样好？

师生活动：学生积极思考，很快算出甲厂的极差是6g，乙厂的极差是9g，得出甲厂产品的质量好，教师引导学生，结合图2进行说明，外贸公司之所以购买甲厂产品，是因为从甲厂产品中抽查的鸡腿质量数据的极差较小，并集中分布在平均质量线附近，说明它的波动性较小，即一组数据的极差越小，这组数据越稳定．

设计意图通过实际问题情境让学生感受仅有平均水平是很难对所有事物进行分析，它需要刻画数据的波动性，从而让学生感受到研究数据波动性的必要性，顺利引入研究数据的其它量度：极差．

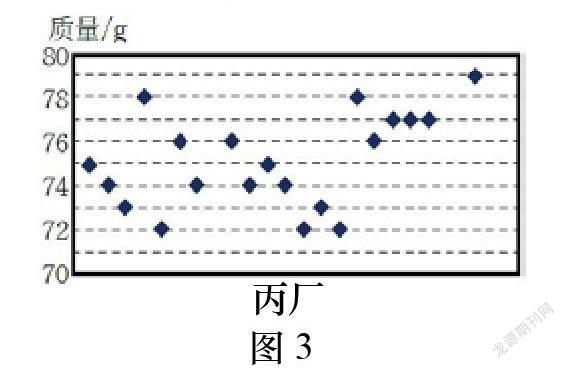
问题2如果丙厂也参与了竞争，从该厂抽样调查了20只鸡腿，它们的质量数据如图3．

（1）丙厂这20只鸡腿质量的平均数和极差分别是多少？

（2）如何刻画丙厂这20只鸡腿的质量与其平均数的差距？分别求出甲、丙两厂的20只鸡腿质量与其相应平均数的差距．

（3）在甲、丙两厂中，你认为哪个厂的鸡腿质量更符合要求？为什么？师生活动：学生很快求出丙厂这20只鸡腿质量的平均数和極差分别是75.1g，7g，这与甲厂鸡腿质量的平均数、极差相近．学生继续思考在甲、丙两厂中，哪个厂的鸡腿质量更加符合要求，教师引导学生观察表1中甲厂和图3乙厂图形的数据分布情况．学生几经讨论都不能断定该如何解释．

设计意图设置知识产生的背景，激活学生的求知欲望，使学生成为探求知识的主人．进而通过对丙厂与甲、乙两厂的对比发现，让学生深刻地意识到，有了极差还不能准确刻画一组数据的离散程度，于是学生急于想解决但仅凭已有的知识又无法解决，这就造成了认知上的“冲突”，为引入方差做好了心理上的准备．

1.2经历过程，形成概念

师：当两组数据的平均数、极差相等或接近时，我们不好说哪组数据波动大，这就需要我们独创一个新的特征量来衡量两组数据的波动大小．

问题3在甲、丙两厂中，当比照对象“平均数”相同或接近（即一般水平相同或接近）时，我们要考虑这组数据的离散程度，即两厂鸡腿质量的稳定程度，但此时“极差”也接近，无法作出决策，那还有没有什么“量”能反映一组数据的离散程度呢？

师生活动：学生先独立思考，再小组交流，教师顺势引导．学生小组讨论片刻后，有学生说，求每个数据与其平均数差（简称“偏差”）的和，通过计算发现，甲、丙两组数据偏差的和都等于0．

追问1：什么原因造成累加之和为0呢？

师生活动：教师引导学生回顾计算的过程，学生很快发现，这些偏差相加，正负相互抵消，

追问2：怎样做才能保证这些“偏差”相加，不会造成正负相互抵消呢？

师生活动：学生探求的热情加上教师的精心引导，思维活跃了，各种想法涌上来，几经筛选，有两个方案，各偏差先取绝对值再相加，或各偏差先平方再相加，第一种方案，学生算出：甲厂数据偏差的绝对值之和为26，丙厂数据偏差的绝对值之和为37，因为37>26，所以甲厂数据比乙组数据“稳定”；第二种方案，学生算出：甲厂数据偏差的平方之和为50，丙厂数据偏差的平方之和为88，因为88>50，所以甲厂数据比乙组数据“稳定”，教师进一步指出，虽然第一种方案在涉及具体数据时较方便，但由于“各偏差先取绝对值再相加”的计算必须依靠绝对值的存在，不适合进一步的代数运算，不利于进一步的统计分析，由此，我们重点研究第二种方案，即“各偏差先平方再相加”的计算方法，

追问3：我们采纳先把各偏差平方再相加的方法，这个“和”不妨用符号y来表示，请同学们计算y甲，y甲·

师生活动：学生很快算出y= 50，y丙=88，显然y甲

设计意图紧张的探索与思考让学生取得了阶段性成功，这容易让学生松懈，一旦松懈下来，思维便会停止不前，这时需要一鼓作气，通过再一次设计新的问题情境来“刺激”他们，以便乘胜追击．

问题4当我们用新设计的特征数y理直气壮地衡量甲厂与丙厂的鸡腿质量时，丙厂却提出了一个条件：仍从我厂产品中抽查20只鸡腿，但要从甲厂的产品中抽查100只鸡腿，同学们是否答应？

师生活动：学生马上表示反对，尽管甲厂产品的质量数据偏差小，较均匀，但多个累加共和必然增大，会导致y甲>y丙，结论会与事实相反．

追问1：看来我们的特征数y还不完善，它受样本容量的影响，换言之，如果两组数据的样本容量不同，样本容量大的其和的值就会相对大，比较两组数据的离散程度时就会因为个数不同而不科学，有没有办法来改进这个量，使其科学公平呢？

师生活动：学习热情再一次被激发，学生努力搜集原有的知识经验，几经争锋，确定两个方法：一是取相同容量的数据，二是求各偏差平方和的平均数．教师顺势引导，学生充分讨论，同意采纳后者来衡量一组数据波动的大小．

追问2：我们将采用“偏差平方和的平均数”这个量来刻画一组数据的离散（波动）程度，同学们能否给这个量命个名字？

追问4：在实际应用中，用方差来描述数据的离散程度时，由于计算中进行了平方，从而可能放大该组数据离散的程度，并且其单位与原来数据的单位不一致，你能继续改进这个量吗？

师生活动：学生积极思考，很快得出求方差的算术平方根，因为开平方和平方相互抵消．教师顺势给出标准差概念就是方差的算术平方根，用“s”表示．教师指出，用标准差刻画一组数据的离散程度更精确、客观．进一步说明标准差的单位与已知数据的单位相同，使用时应当标明单位；方差的单位是已知单位的平方，使用时可以不标明单位，

问题5分析方差公式，你发现用方差刻画一组数据的波动大小时有什么规律吗？请分别计算甲、丙两厂鸡腿质量的方差进行验证，

师生活动：学生结合甲、丙两厂的数据分布图与方差计算公式，分组讨论．教师听取学生的意见，引导学生分析，找出规律：当数据分布比较分散（数据在平均数附近波动较大）时，各个数据与平均数的平方和较大，方差就越大，反之亦然，即：一组数据的方差越小，这组数据就越稳定，学生分组计算后，进一步感受方差描述数据波动大小的合理性，理解用方差刻画一组数据波动大小的合理性．两组数据的方差分别是：

显然s甲

设计意图选取一个实际问题作为探究的线索，完整地展示“发现问题、寻找解决方法、不断完善方法”的过程，学生对概念的形成不仅身临其境，而且还让学生经历了“分析数据”的一个完整过程，从而使一个冗长难懂的概念变得清晰合理，就这样，在教师层层引导下，学生知道了为什么要引入方差，在引入方差过程中为什么要“先平均，再作差，然后平方，最后再平均”，在这一系列问题都解决后，方差的概念也就清晰了．更重要的是，通过这样的引导，学生除了能更轻松、自然地掌握方差概念之外，还经历了一次充满探究解决问题的过程．这个过程，是学生学习数学中收获的最主要、本质的能力，即数据分析这一数学核心素养．

1.3应用概念，解决问题

师：请用你所学统计知识，解決下面的问题，并说明理由．

问题6甲、乙两支仪仗队队员的身高（单位：cm）如下：

甲队：178， 177， 179， 179， 178， 178， 177，178， 177， 179；

乙队：178， 177， 179， 176， 178， 180， 180，178， 176， 178．

哪支仪仗队队员的身高更整齐？怎么判断？

追问1：题目中“整齐”的含义是什么？思考在这个问题中要研究一组数据的什么特征？

追问2：在求方差之前先要求哪个统计量？

追问3：你能总结用方差估计数据波动程度的步骤吗？

师生活动：教师引导学生分析题意，板书解题过程，学生思考问题，并和教师一起计算、判断、解决问题，同时提出问题：我们在什么情况下才会比较方差？进一步加深学生对方差的理解．

设计意图该例题是关于方差的定义和方差的意义的实际应用，通过该例题，让学生进一步理解方差的意义，进一步熟悉公式的计算过程：先计算平均数，再作差，然后平方，最后再平均，进而规范解题格式和步骤．

1.4 归纳小结，拓展升华

师：今天我们学习了刻画数据离散程度的三个“特征量”，请大家结合下面几个问题，一块回顾下．

问题6 （1）方差是反映一组数据的离散程度的，极差也是反映一组数据的离散程度的，极差计算方便，方差计算复杂，学习了极差为什么还要学方差？ （2）方差如何计算？方差的大小和数据的波动程度有何关系？如何理解方差的意义？ （3）回顾方差概念的学习，你经历了一次怎样的探究、解决问题的过程？ （4）除了极差、方差和标准差，还有没有其他数据可以刻画数据的离散程度？思考不使用这些数据的原因．（5）教材的例题，练习中比较两组数据的离散程度时的两组数据的平均数都相同，请问比较两组数据方差时一定要平均数相同吗？ （6）对知识的理解，很大程度上是关注有关概念在实际问题情境中的意义，对于平均数、中位数、众数、极差、方差、标准差等概念，你是否能够区分它们在具体情境中的意义？

师生活动学生先谈一谈本节课的收获，教师再加以总结，并用框图1，2梳理统计相关概念的知识系统，形成对相关知识的结构性理解．

设计意图设置这些问题，意在让学生畅所欲言，共同交流．这不仅仅对本节课所学知识、思想方法进行总结，还可以交流自己在学习过程中的一些感受，最终的目的是发展学生的数学核心素养（数据分析），增强学生的反思意识，进一步让学生认识数据离散程度的意义和影响．

1.5布置作业，深化提高

必做题：课本习题6.5第1，2，3题．

选做题：课本习题6.5第4题．

拓展题请用方差来解释“共同富裕”，并谈谈方差对教育的启示，

设计意图适量课外作业可以加强学生对所学知识的巩固，防止知识遗忘，而作业设置三个梯度，是为了满足不同层次学生的需要，作业分层布置，真正实现“不同的人在数学上得到不同的发展”．

2 设计说明

本节课的设计理念是以现实问题为知识背景，围绕如何构造方差展开探究尝试，以理解数学的本质为前提，以解决问题为知识线索，以培养数学思维能力为重点，以激发求知欲和好奇心为关键，让学生了解了用来刻画一组数据离散程度的三个新“特征量”产生的背景和应用，体验了数学发现和创造的历程，在教学环节的设计上，摒弃了“灌输和操练”，也不再单纯的依赖于记忆和套路，而是通过问题引导学生主动学习，这不但體现了教师为主导、学生为主体的教学原则，而且还实现了培养学生科学的探究精神和创造能力的目标，教与学的过程，始终以问题展开新知探究，并不断地通过追问以问题链的形式引导学生从知识的发生、发展处寻根求源，如此设计既有生命能量，又能触发学生更深的思考，从而使一个陌生繁杂的概念变得清晰直观，达到对概念的正确认识，有效地克服了难点，培养了学生良好的学习动机和浓厚的学习兴趣．

由此可见，“统计”概念课的教学设计，教师同样不应该只告诉学生“做什么”和“怎么做”，更应该让他们知道“为什么”．只有遵循“统计”的课程理念，发展数据分析的数学核心素养，认真研读教材，关注概念的形成过程，才能真正做到以生为本，激活学生思维，进而设计有效乃至高效的教学方案．

参考文献

[1]中华人民共和国教育部制定，义务教育数学课程标准（2011年版）[S]．北京：北京师范大学出版社，2012

[2]义务教育课程标准修订组．义务教育数学课程标准（2011年版）解读[M]．北京：北京师范大学出版社，2012