基于有限时间神经网络求解的时变复数矩阵方程

高 畅,孔 颖,胡汤珑

(浙江科技学院 信息与电子工程学院,杭州 310023)

矩阵方程求解在工程实践中有着非常广泛的应用场景,例如多进多出(multiple-input multiple-output,MIMO)技术[1]、现场可编程逻辑门阵列(field-programmable gate array,FPGA)设计[2]和机械臂应用[3]。矩阵方程的求解主要有两种方法:第一种方法是使用基于迭代思想产生的传统数值算法,如近似迭代法[4]、蒙特卡罗方法[5]和插值分解法[6],由于数值算法计算的串行性,使用它们来处理大规模数据和高维数矩阵时,迭代计算的性能可能不够高;第二种方法是使用一些神经网络算法[7-8],神经网络算法具有高速并行处理数据的能力且能够实时运算,因此在求解高维数矩阵方程和复杂的时变矩阵方程时,计算性能较高。

基于标量取值能量函数的梯度神经网络(the gradient-based neural network,GNN)是一种传统的神经网络,可用于求解矩阵方程。然而,GNN在求解过程中基本上都只考虑静态情况,它不会考虑时变情况造成的影响。因此在求解过程中,它的估计误差可能不会收敛到零。因此,使用该方法求解时变矩阵方程时,精度不高。

为实时求解时变矩阵方程,张雨浓提出了一种归零神经网络(zeroing neural network,ZNN)[9-10]。ZNN是一种递归神经网络,它可以有效地解决GNN中存在的估计误差收敛问题[11],它的估计误差会随时间的变化而最终收敛到零。因此,ZNN能得到时变矩阵方程的准确解。但是,ZNN只能用于求解实数域中的时变矩阵方程,不能作用于复数域。目前,许多时变问题需要进一步考虑到复数域的情况。如计算机视觉中的图像处理[12]和计算机科学中的模式识别[9]。针对上述问题,一些研究者提出了能应用于复数域中的神经网络(complex-valued zeroing neural network,CVZNN)[11,13-14]。但用CVZNN求解时变复数问题时,收敛速度较慢、计算精度不高。根据文献[13],神经网络的收敛速度、计算精度与网络的设计参数和选取的激励函数有关。因此,可以考虑选取实数域中的一些激励函数,将其扩展到复数域,以此来提高神经网络的稳定性和收敛性。

针对时变复数矩阵方程的求解问题,本文首先提出两种新型有限时间归零神经网络(new finite-time zeroing neural network,NFTZNN)模型,该模型在求解上述问题时性能较好。然后,根据李亚普洛夫定理计算出收敛时间上界,再进行稳定性和收敛性的证明来验证理论分析的有效性。最后,通过仿真试验,可验证理论推导的可行性。

1 问题提出和ZNN模型

一般情况下,定义一个时变复数矩阵方程为

F(t)Z(t)=I。

(1)

式(1)中:t表示时间。给定光滑的时变复数矩阵F(t)∈Cn×n和单位矩阵I∈Cn×n,求满足方程的复数矩阵Z(t)∈Cn×n。上述矩阵的维数都是n行n列。因为矩阵F(t)和Z(t)是时变复数矩阵,矩阵中的所有元素都是复数且会随时间变化,所以求解出的Z(t)需要在任意时刻t都满足式(1)。

为实时求解时变复数矩阵方程(1),仿照实值域中ZNN的设计方法[13,15],构造出能应用于复数域的标准ZNN模型。

首先,为估计实际解Z(t)与理论解Z*(t)之间的计算误差,定义误差矩阵E(t)∈Cn×n。当E(t)趋于零时,此时方程中的Z(t)就是方程的理论解Z*(t),误差矩阵

E(t)=F(t)Z(t)-I。

(2)

然后,引入标准ZNN设计公式:

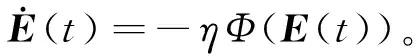
(3)

最后,联立式(2)和式(3),得到时变复数矩阵方程(1)的标准ZNN模型为

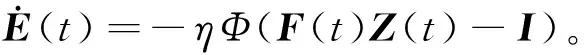
(4)

2 NFTZNN模型

首先在标准ZNN模型(4)的基础上,将实数域中的非线性激励函数扩展到复数域,根据复数域中两种等价地处理非线性激励函数的方法,构建出两种NFTZNN模型。然后,引入了一种新型激励函数来提高两种NFTZNN模型的收敛速度和计算精度。最后,将两种新构建的NFTZNN模型分别命名为NFTZNN-Ⅰ模型和NFTZNN-Ⅱ模型。

2.1 NFTZNN-Ⅰ模型

处理式(4)中非线性激励函数的第一种方法是同时处理复数输入的实部与虚部,具体定义描述如下:

Φ1(E(t))=Ω(U(t))+iΩ(V(t))。

(5)

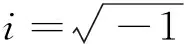
联立式(3)和式(5),可得:

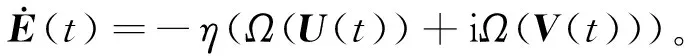
(6)

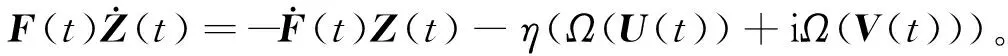
(7)

2.2 NFTZNN-Ⅱ模型

处理式(4)中非线性激励函数的第二种方法是处理复数输入的模,具体定义描述如下:

Φ2(E(t))=(Ω(C(t))∘exp(iD(t)))。

(8)

式(8)中:∘为矩阵之间的哈达玛积;C(t)和D(t)分别为误差矩阵E(t)的模与辐角。

联立式(3)和式(8),可得

(9)

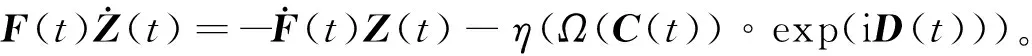
(10)

2.3 新型激励函数

针对复数域中时变问题的求解,将实数域中的非线性激励函数应用到CVZNN模型中,提高了模型的收敛速度[13]。其中,将符号双幂(sign-bi-power,SBP)激励函数应用到CVZNN模型中,可以实现有限时间收敛,并能计算出收敛时间上界。因此,可以寻找一种合适的非线性激励函数,将它应用到NFTZNN-Ⅰ模型(7)和NFTZNN-Ⅱ模型(10)中,来加快两种模型的收敛速度、提高其计算精度。因此,选用新型激励函数

f(x)=a1|x|ksign(x)+a2x,a1>0,00。

(11)

式(11)中:a1、k和a2为激励函数的设计参数;sign(·)为符号函数。新型激励函数是单调递增的奇函数,证明如下

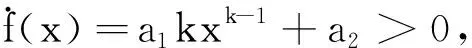
根据文献[11],将它应用到两种NFTZNN模型时可以保持全局收敛。另外,为进行对比试验,列举出SBP激励函数

(12)

式(12)中:r为SBP激励函数的设计参数。

3 理论分析

本节给出四个定理,前两个定理说明当两种NFTZNN模型应用单调递增的奇函数,并被用来求解时变复数矩阵方程时,能收敛到理论解。后两个定理说明当两种NFTZNN模型应用新型激励函数(11),其在求解时变复数矩阵方程时,能在有限时间内收敛到理论解,并可以计算出收敛时间上界。

3.1 稳定性分析

定理1 给定光滑的时变复数矩阵F(t),如果将单调递增的奇函数f(·)应用到NFTZNN-Ⅰ模型(7),那么通过NFTZNN-Ⅰ模型(7)求解的未知矩阵Z(t)从任意初始状态Z(0)开始,最终能收敛到时变复数矩阵方程的理论解Z*(t)。

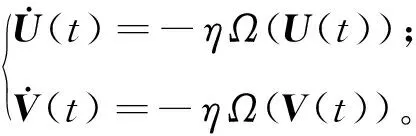
(13)

取矩阵U(t)和V(t)中的各个元素,可得:

(14)

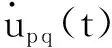
定理1成立。

定理2给定光滑的时变复数矩阵F(t),如果将单调递增的奇函数f(·)应用到NFTZNN-Ⅱ模型(10),那么通过NFTZNN-Ⅱ模型(10)求解的未知矩阵Z(t)从任意初始状态Z(0)开始,最终能收敛到时变复数矩阵方程的理论解Z*(t)。

证明:根据式(9),可得:

(15)

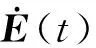
(16)

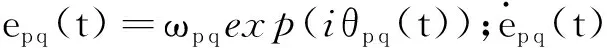
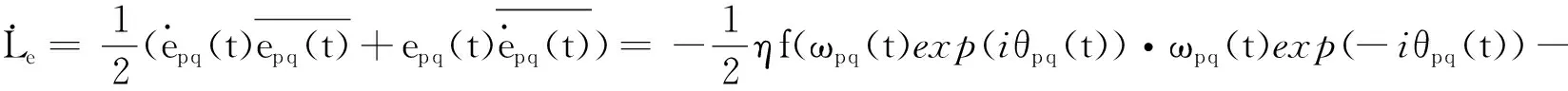
(17)

定理2成立。

3.2 收敛性分析

定理3给定光滑的时变复数矩阵F(t),如果将新型激励函数(11)应用到NFTZNN-Ⅰ模型(7),那么通过NFTZNN-Ⅰ模型(7)求解出的未知矩阵Z(t)从任意初始状态Z(0)开始,最终能在有限时间后收敛到时变复数矩阵方程的理论解Z*(t)。NFTZNN-Ⅰ模型(7)的收敛时间上界

(18)

式(18)中:m(0)=max{|up q(0)|,|vp q(0)|};up q(0)和vp q(0)分别为误差矩阵E(0)第p行第q列元素的实部与虚部。

证明:根据式(14),可得:

(19)

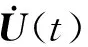
(20)

首先定义李亚普诺夫函数L(t)=|m(t)|2,对它求导:

(21)

将式(21)两边同乘e2η a2t,化简得:

(22)

最后将微分方程(22)两边同时积分,解得:

(23)

由于L(t)=|m(t)|2,故L(t)≥0,因此式(22)中-2ηa1e(1-k)η a2t≥0,可以解得:

定理3成立。

定理4给定光滑的时变复数矩阵F(t),如果将新型激励函数(11)应用到NFTZNN-Ⅱ模型(10),那么通过NFTZNN-Ⅱ模型(10)求解出的未知矩阵Z(t)从任意初始状态Z(0)开始,最终能在有限时间后收敛到时变复数矩阵方程的理论解Z*(t)。NFTZNN-Ⅱ模型(10)的收敛时间上界

(24)

式(24)中:n(0)=max{|ep q(0)|},ep q(0)分别为误差矩阵E(0)的第p行第q列元素的初始状态。

证明:定义李亚普诺夫函数L(t)=|n(t)|2,n(0)是E(t)所有元素中模数的最大值,且初始状态n(0)=max{|ep q(0)|}。可以得出结论,当n(t)趋于零时,E(t)中所有元素都会等于零。因此,若计算出n(t)的收敛时间,就能估算出NFTZNN-Ⅱ模型(10)的收敛时间上界。根据式(16),可以得到n(t)的动态表达式:

(25)

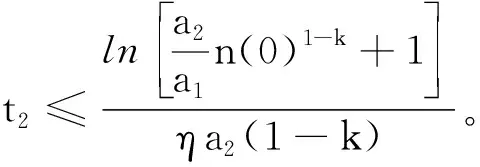
定理4成立。

4 仿真实例

以下通过求解一个时变复数矩阵方程,并在方程中使用不同的矩阵系数,得到两个不同的算例,从而证明使用新型激励函数的NFTZNN-Ⅰ模型(7)和NFTZNN-Ⅱ模型(10)求解时变复数矩阵方程时能保证全局收敛。此外,为说明误差收敛速度的改进,将新型激励函数(11)与SBP激励函数(12)进行比较,并计算出了各自的收敛时间上界。

仿真1 考虑时变复数矩阵方程F(t)Z(t)=I,已知F(t)和单位矩阵I,求未知矩阵Z(t),矩阵系数如下:

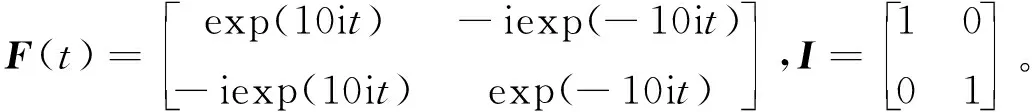
在这种情况下,计算出Z(t)的理论解为

图1为仿真1中NFTZNN-Ⅰ模型和NFTZNN-Ⅱ模型中Z(t)的轨迹变化,描述了使用新型激励函数(11)的NFTZNN-Ⅰ模型(7)和NFTZNN-Ⅱ模型(10),用来求解时变复数矩阵方程时未知矩阵Z(t)的阶段性变化(两种NFTZNN模型中设定η=40,a1=0.6,k=0.5,a2=1)。图中红色实线表示实际解Z(t)的状态变化,蓝色虚线表示理论解Z*(t)的状态变化。图中实线与虚线会在一段时间后重合,这说明Z(t)从初始状态Z(0)开始(仿真中初步设定初值Z(0)=[1+i,1;1+i,1]),最终能在一段时间后收敛到时变复数矩阵方程的理论解Z*(t)。

图1 仿真1中NFTZNN-Ⅰ模型和NFTZNN-Ⅱ模型中Z(t)的轨迹变化Fig.1 Trajectory change of Z(t) in NFTZNN-Ⅰ model and NFTZNN-Ⅱ model in simulation 1

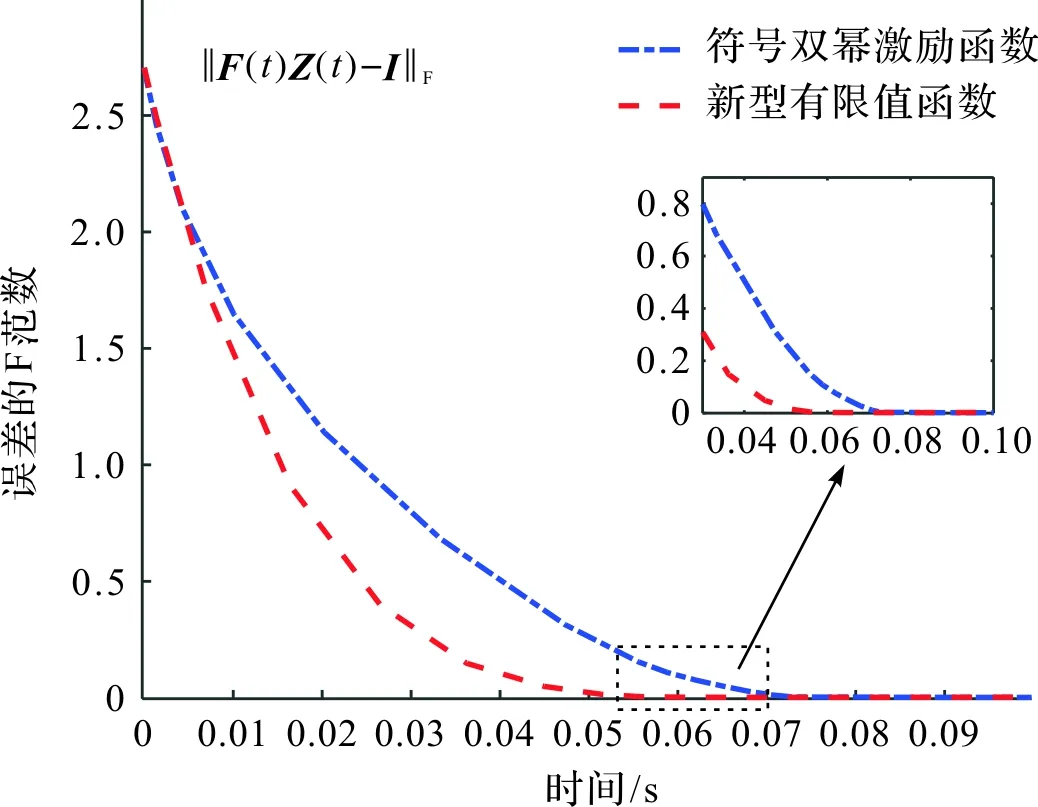
图2 仿真1中新型激励函数与SBP激励函数 的收敛性比较Fig.2 Convergence comparison between new activation function and SBP activation function in simulation 1

图3为仿真1中设计参数k的收敛性比较,描述了用NFTZNN-Ⅰ模型(7)来求解时变复数矩阵方程时,设计参数k对误差收敛速度的影响(固定η=40,a1=0.6,a2=1)。从图3中可以看出,k越接近于零,误差的收敛速度越快。

图4为仿真1中设计参数η的收敛性比较,描述了用NFTZNN-Ⅰ模型(7)来求解时变复数矩阵方程时,设计参数η对误差收敛速度的影响(固定a1=0.6,k=0.5,a2=1)。从图4中可以看出,η越大,误差的收敛速度越快。

图3 仿真1中设计参数k的收敛性比较Fig.3 Convergence comparison of design parameter k in simulation 1

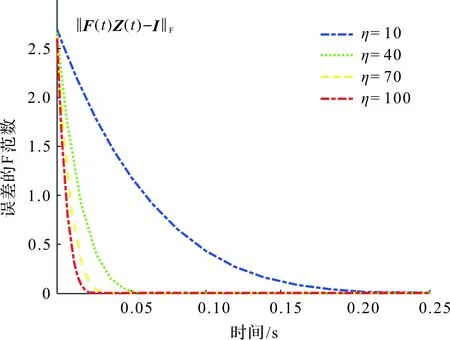
图4 仿真1中设计参数η的收敛性比较Fig.4 Convergence comparison of design parameter η in simulation 1

仿真2 考虑时变复数矩阵方程F(t)Z(t)=I,已知F(t)和单位矩阵I,求未知矩阵Z(t),矩阵系数如下:

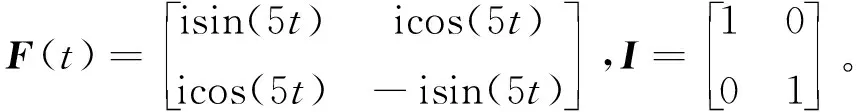
在这种情况下,计算出Z(t)的理论解为

图5为仿真2中NFTZNN-Ⅰ模型和NFTZNN-Ⅱ模型中Z(t)的轨迹变化,描述了使用新型激励函数(11)的NFTZNN-Ⅰ模型(7)和NFTZNN-Ⅱ模型(10),用来求解时变复数矩阵方程时未知矩阵Z(t)的阶段性变化(两种NFTZNN模型中设定η=40,a1=0.6,k=0.5,a2=1)。图中实线与虚线会在一段时间后重合,这说明Z(t)从初始状态Z(0)开始(仿真中初步设定初值Z(0)=[3+2i,4+i;2-i,3+i]),最终能在一段时间后收敛到时变复数矩阵方程的理论解Z*(t)。

图5 仿真2中NFTZNN-Ⅰ模型和NFTZNN-Ⅱ模型中Z(t)的轨迹变化Fig.5 Trajectory change of Z(t) in NFTZNN-Ⅰ model and NFTZNN-Ⅱ model in simulation 2

图6 仿真2中新型激励函数与SBP激励 函数的收敛性比较Fig.6 Convergence comparison between new activation function and SBP activation function in simulation 2

图7为仿真2中设计参数k的收敛性比较,描述了用NFTZNN-Ⅱ模型(10)求解时变复数矩阵方程时,设计参数k对误差收敛速度的影响(固定η=40,a1=0.6,a2=1)。从图7中可以看出,k越接近于零,误差的收敛速度越快。

图8为仿真2中设计参数η的收敛性比较,描述了用NFTZNN-Ⅱ模型(10)求解时变复数矩阵方程时,设计参数η对误差收敛速度的影响(固定a1=0.6,k=0.5,a2=1)。从图8中可以看出,η越大,误差的收敛速度越快。

图7 仿真2中设计参数k的收敛性比较Fig.7 Convergence comparison of design parameter k in simulation 2

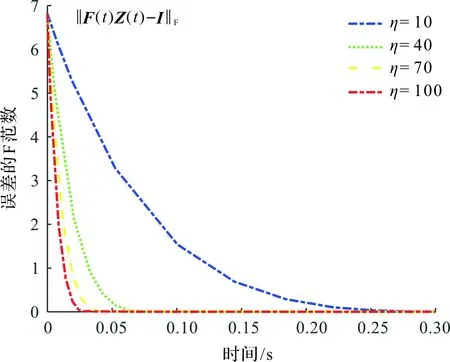
图8 仿真2中设计参数η的收敛性比较Fig.8 Convergence comparison of design parameter η in simulation 2

5 结 语

本研究针对时变复数矩阵方程的求解,提出了两种新型有限时间归零神经网络(NFTZNN)模型。将一种新型激励函数(11)应用到NFTZNN-Ⅰ模型(7)和NFTZNN-Ⅱ模型(10)中,加快两种模型的收敛速度,提高其计算精度。与传统的SBP激励函数(11)相比,应用新型激励函数的两种NFTZNN模型在求解时变复数矩阵方程时,收敛速度更快,收敛时间上界更小。理论分析和数值仿真证明了方法的有效性和可行性。但是,因为新型激励函数是非线性函数,所以使用新型激励函数的NFTZNN模型求解时变复数矩阵方程时,与传统的CVZNN模型相比具有更高的复杂度。未来的研究中可能会考虑噪声对两个NFTZNN模型的影响。