基于曲面分层的大型螺旋桨GMA 增材制造

李鑫磊，韩庆璘，张广军

(哈尔滨工业大学,先进焊接与连接国家重点实验室,哈尔滨,150001)

0 序言

目前，增材制造技术是世界各国争先发展的新型制造技术之一[1-5].成形精度和成形效率的矛盾是增材制造需要解决的主要问题，获得金属增材制造成形精度和成形效率的最优匹配控制策略，实现高精度、高效率增材制造是科技人员追求的目标.

解决成形精度与效率的矛盾，分层切片是关键环节.对于复杂曲面的增材制造，传统的平面分层会出现严重的台阶效应.尤其对于单层高度较大的增材制造方法，如熔化极气体保护电弧(gas metal arc，GMA)增材制造，台阶效应会更加明显，也会增加零件表面的粗糙度，严重影响成形精度.

曲面分层增材制造是指使用一组空间等距曲面代替平面来分割零件三维模型的增材制造方法.相对平面分层，具有以下优势：①表面成形质量更好，减少了大曲率零件采用平面分层时出现的台阶效应；②总熔敷层数更少，单条熔敷道长度更长，熔敷效率更高；③起弧点、熄弧点更少，成形质量更好.独特的优势使曲面分层更适合于表面曲率较大的零件，如螺旋桨.

目前曲面分层算法相关研究较少，He 等人[6]提出了以圆柱面代替平面的方式进行分层切片，实现了柱面分层算法，然而该算法对于一般性的曲面并不适用.Yashpal 等人[7]提出采用 B 样条曲面方程来拟合曲面方法，从而实现了样条曲面分层，该方法控制点需要手动选取，控制点数量有限无法拟合复杂曲面.

曲面分层作为一种新的增材制造模式，还处于萌芽和初步探索阶段，特别是对于 GMA 增材制造，曲面分层方法还存在很多问题.为此，研究了适用于任意曲面的通用曲面分层方法及空间曲面等距轮廓偏置路径规划算法，并将其应用到直径为1 m的扭转棱形螺旋桨机器人GMA 曲面分层增材制造上，扩展了GMA 增材制造的实现方式和研究范围.

1 曲面分层算法

开发的曲面分层算法包括初始分层曲面的确定、等距分层曲面的生成、分层曲面与模型相交轮廓的计算3 个部分.

等距曲面的生成是曲面分层算法的核心内容.为了保证各个位置层间距相同，沿法向平移曲面.而增材制造中使用的光固化立体造型术(stereolithography，STL)模型是由一系列带有法向的空间三角片组成的，由于相邻三角片的法向不同，若直接沿着各自法向平移三角片，得到的分层曲面上三角片之间会出现空隙或重叠.图1 为平移三角片和平移控制点的对比效果.如直接平移三角片，无法生成连续平滑的分层曲面，如图1a 所示.提出平移三角片顶点的思路实现曲面平移，以避免这种情况发生.

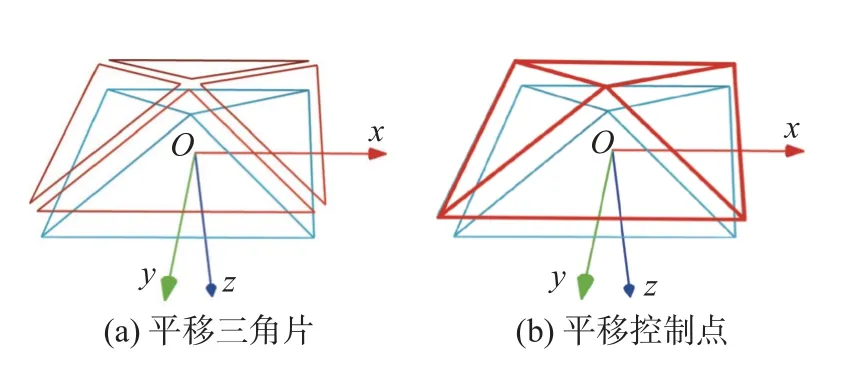
图1 STL 曲面平移方式Fig.1 STL surface translation mode.(a) translate triangle;(b) translate control points

考虑到STL 模型中三角形顶点被多个三角形共有，而这些三角形的法向并不相同，需要综合考虑来确定顶点的平移方向.如图2 所示，当点A 被m个三角片共同拥有时，A 点的平移方向n的计算如式(1)所示，图中B，C，D，I，J，M，N 代表三角网格顶点.

图2 三角片顶点平移方向的确定Fig.2 Determination of triangle vertex translation direction

式中：ni为 第i个三角片的法向；ai为第i个三角片中角i的大小；∂i为角ai所占的比重；n为A 点最终的平移方向.图3 和图4 分别为初始分层曲面为圆柱面、梭形曲面时生成的分层面及与模型相交得到的轮廓.

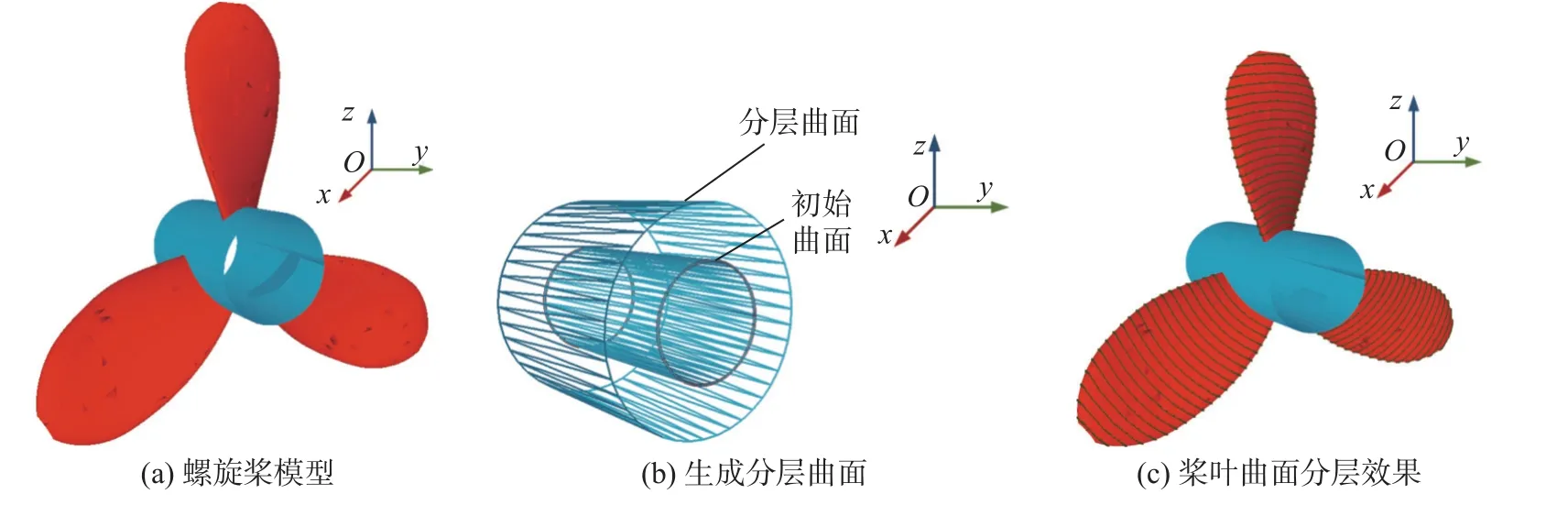
图3 初始分层曲面为圆柱面时生成的分层面和相交轮廓的三维图Fig.3 Generated layers and 3D diagram of intersecting contours when curved layer with cylindrical initial surface.(a) propeller model;(b) generated layered surface;(c) propeller curved layering result

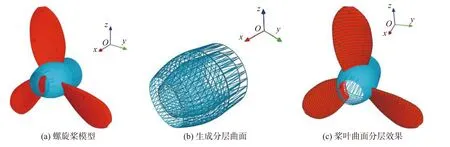
图4 初始分层曲面为梭形时生成的分层面和相交轮廓的三维图Fig.4 Generated layers and 3D diagram of intersecting contours when curved layer with spindle initial surface.(a) propeller model;(b) generated layered surface;(c) propeller curved layering result

沿着每个顶点的平移方向平移初始曲面上的顶点，并保持初始曲面在STL 模型中的拓扑关系，得到新的三角片便构成了连续平滑的等距分层曲面，如图3b 和图4b 所示.依次遍历所得到的分层曲面中的三角片与零件 STL 模型的三角片，并计算两个三角片相交产生的线段.将所有线段首尾相连，便构成这一层的分层轮廓，如图3c 和图4c 所示.

2 曲面轮廓等距偏置路径规划算法

为了保证相邻的熔敷道搭接平整，得到厚度均一的曲面等厚熔覆层，有必要对曲面上的等距路径规划进行研究.与平面上的等距路径规划相比，由于曲面上的曲率是在不断变化的，无法沿着某一个固定的方向进行平移.

提出了一种基于体素化和曲线积分思想的空间曲面上等距路径规划算法.算法具备不会生成局部自交与全局自交环，并对曲面曲率变化的形式、曲面模型三角网格的大小均不敏感，适用于任意形式的空间曲面等优势.算法的具体实现参考李鑫磊等人[8]开展的电弧增材制造中空间曲面等距路径规划算法研究.

图5 为在曲面进行轮廓偏置路径规划的中间步骤及最后效果，算法基本步骤如下.

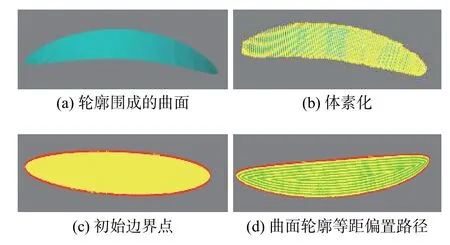
图5 空间曲面轮廓偏置路径规划算法Fig.5 Spatial curved surface contour offset path planning algorithm.(a) curved surface from contour siege;(b) voxelization result;(c) initial boundary point;(d) equidistant curved surface contour offset path

(1)体素化.将分层曲面与螺旋桨叶片相交得到的外轮廓所围成的曲面体素化(分割为众多的小立方体)，并给每一个体素点分配一个属性，代表自己到轮廓的距离.采用kd-tree 结构储存所有的体素点，来优化点云临域查找速度.如图5b 所示.

(2)确定初始点集.遍历所有体素点，将与轮廓距离小于设定阈值的点作为初始点，并将初始点的距离设为0，如图5c 所示.

(3)确定平移点集.将体素点中与初始点直接相邻的点作为下一次迭代中要计算距离的平移点.

(4)计算平移点到初始边界的距离.遍历平移点，计算从初始点指向平移点的平移向量.平移点到轮廓的距离等于平移向量在法平面上的投影长度与初始点的距离之和.

(5)将平移点集插入初始点集，然后重复上述的(3)～ (4)步，即得到了所有点到轮廓的曲面距离.

(6)最后遍历所有的点，其距离为偏置距离整数倍的点，选中为路径点，如图5d 所示.

3 试验验证

以直径为1 m 的扭转棱形螺旋桨为例，进行机器人GMA 曲面分层增材制造验证试验.螺旋桨电弧增材系统的工作过程为：首先，根据熔敷道模型数据库推荐的合理的层高，生成等距分层曲面，并计算分层曲面与模型之间的相交轮廓；其次，结合数据库推荐的道间距，在分层曲面上生成等距轮廓偏置路径；然后，在参数规划模块中，使用层高及道宽查询模型数据库，得到对应的熔敷电流、电压、行走速度；最后，结合规划的焊枪运动轨迹与熔敷参数，生成机器人执行程序.整个螺旋桨曲面分层机器人GMA 增材制造过程如图6 所示.

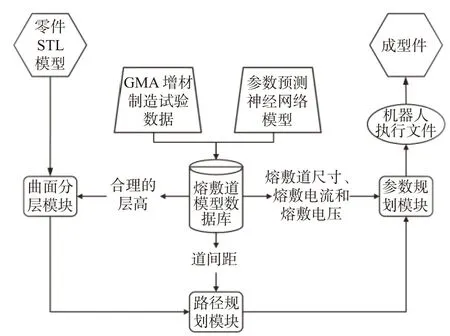
图6 螺旋桨曲面分层机器人GMA 增材制造过程Fig.6 Curved layered robot GMA additive manufacturing process of propeller

图7 为机器人GMA 增材制造的硬件系统，包括Motorman MH24 六轴机器人、旋转倾斜变位机、Panasonic YD-500FR 焊机等.

图7 系统硬件实物图Fig.7 Physical hardware system diagram

桨叶采用空心减重设计，每层由一条熔敷道构成，熔敷道的路径由开发的曲面等距轮廓偏置路径算法规划得到.

螺旋桨直径为1 m，中心轴外径为0.2 m.规划层高度为1.6 mm，熔敷道宽度6.0 mm，共规划堆敷250 层.查寻熔敷道模型数据库，得到工艺参数如下：熔敷电流为130 A，熔敷电压为21.5 V，熔敷速度为5.5 mm/s.试验采用直径1.2 mm 的H08Mn2Si焊丝作为填充材料和Q235B 圆柱金属管作为基板，保护气体采用95%Ar+5%CO2的混合气体，保护气体流量设置为18 L/min ± 0.5 L/min.

图8 为单个螺旋桨叶片采用曲面分层和平面分层的对比.采用平面分层时，总高度为417.2 mm，需要261 层，与曲面分层相比，总层数增加，熔覆效率低；同时，在叶片根部区域会出现很小的熔覆层，导致成形精度低、叶片与中心轴连接处性能差等问题.熔敷过程及最终成形效果如图9 所示.

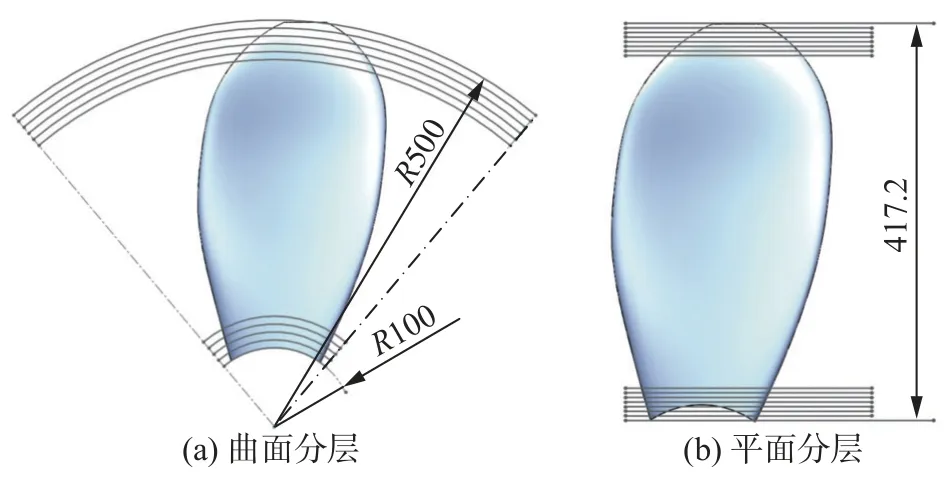
图8 螺旋桨平面与曲面分层对比(mm)Fig.8 Comparison of plane layering and curved layering.(a) curved layer;(b) plane layer

图9 螺旋桨增材制造堆敷过程Fig.9 Propeller additive manufacturing process.(a) 1th layer;(b) 30th layer;(c) 100th layer;(d) overall appearance

为了验证螺旋桨成形精度，采用手持式三维扫描仪对螺旋桨进行三维扫描重建，并与标准模型进行比对，进而统计各个位置与标准模型的误差，其效果如图10 所示.图10a 为螺旋桨的标准模型，图10b 为螺旋桨的扫描模型，采用武汉中观自动化科技有限公司生产的ZG Scan 型扫描仪进行扫描，其测量精度可达0.05 mm.由于标准模型与扫描模型的坐标系不同，不能直接进行对比，首先要通过迭代最近点(iterative closest point，ICP)算法，将其统一到相同的坐标系后进行对比.上述过程通过Geomagic 点云处理软件实现，对比结果如图10c 所示，可见桨叶成形最大偏差在3.0 mm 以下，标准偏差为1.1 mm.

图10 螺旋桨成形精度分析Fig.10 Analysis of propeller forming accuracy.(a) standard model;(b) scanning model;(c) forming dimension error

4 结论

(1) 提出了基于从空间角加权法向方向平移三角网格控制点策略的平移算法，实现了复杂曲面的高适应性曲面分层.采用基于体素化的等距路径规划算法，得到了叶片的曲面轮廓等距偏置路径.

(2) 采用GMA 曲面分层增材制造的方法，堆敷了一个直径为1 m 的扭转棱形螺旋桨.论证了曲面分层相较于平面分层针对螺旋浆等大曲率零件的优势.桨叶的成形尺寸标准偏差为1.1 mm，最大偏差在3.0 mm 以下.