空间曲线的一种微分中值定理

牛丽娜，热比古丽·吐尼亚孜

空间曲线的一种微分中值定理

牛丽娜，热比古丽·吐尼亚孜

（新疆理工学院 理学院，新疆 阿克苏 843100）

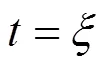
空间曲线；切向量；方向导数；可微；微分中值定理

1　引言及预备知识

在一元函数微分中值定理中，有许多文献给出了拉格朗日中值定理的不同证明方法[1-4]．从拉格朗日中值定理的物理学意义出发，考察平面上两条相交的连续曲线在交点对应区间的两端点内部某一点处函数的导数之间的关系，可以得到定理１．

由定理1可以得到经典的拉格朗日中值定理，也可得到推论．

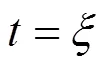
2　主要结果及证明

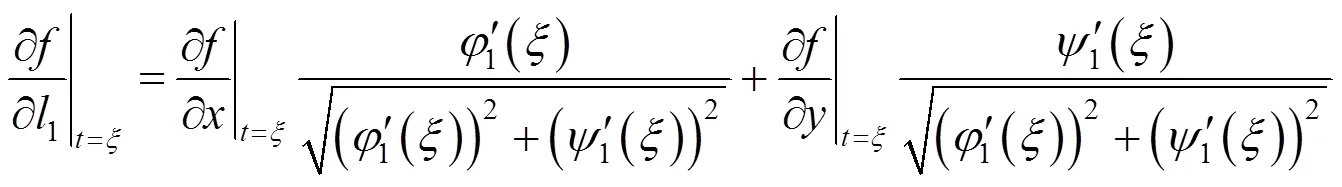
于是有

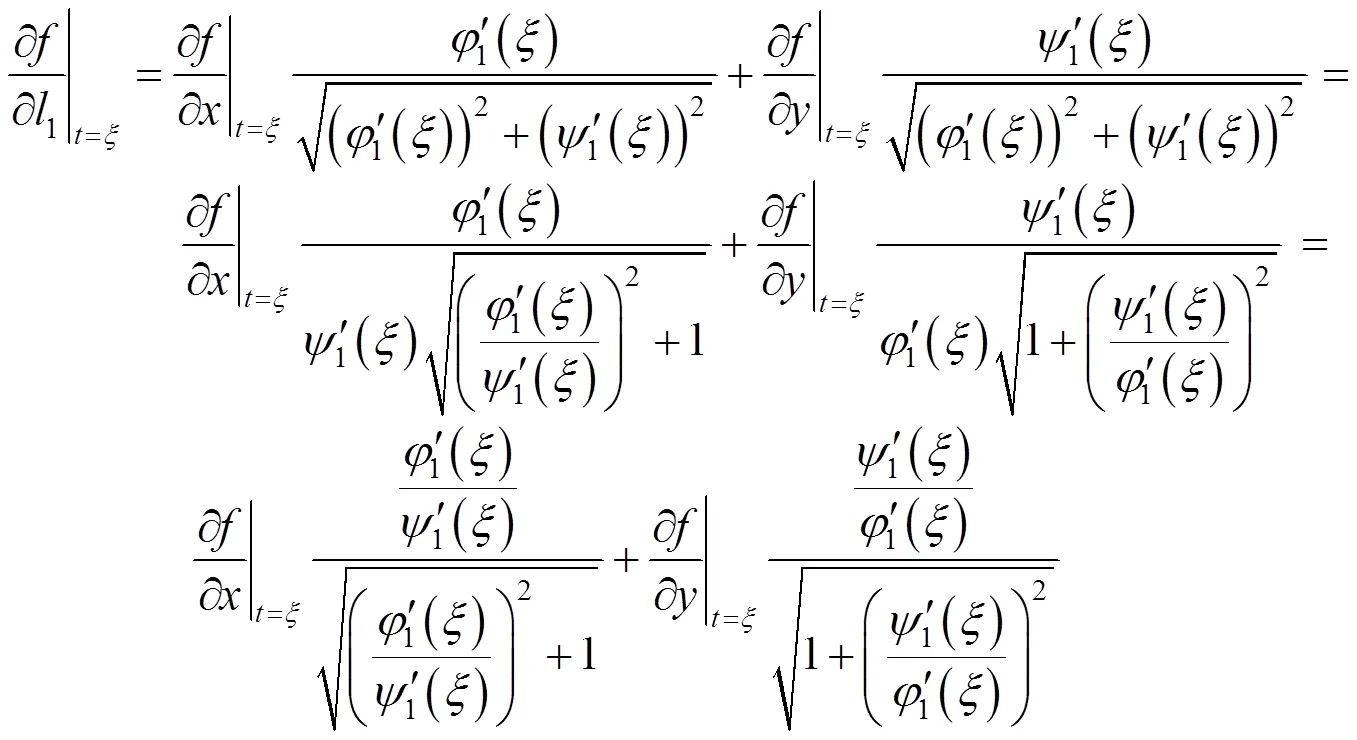
证毕．

进一步地由引理可得

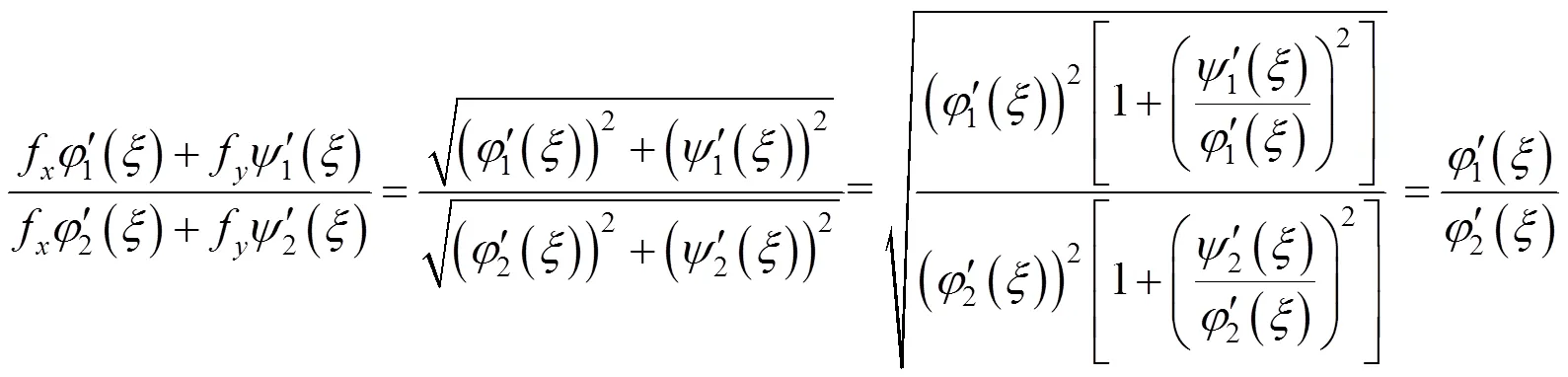
3　结语

从证明平面上两条相交光滑曲线在相交区间内某一点处切线平行的性质出发, 推导出曲面上两条相交光滑曲线在某一点的切向量平行. 这一结果对于加强空间曲线微分学的教学和引导学生更好地认识空间曲线导数间的关系具有一定的帮助作用．

致谢衷心感谢李会师教授提出本文论题并对文章的写作给予细心指导．

[1] 同济大学数学系．高等数学：上[M]．7版．北京: 高等教育出版社，2014：125-131．

[2] 华东师范大学数学科学学院．数学分析：上[M]．5版．北京: 高等教育出版社，2019：111-115．

[3] 王建云，全宏波，赵育林．浅谈拉格朗日中值定理的几种证明方法[J]．数学学习与研究，2021（7）：150-151．

[4] 时秀娟．拉格朗日中值定理证明中辅助函数的不同构造方法[J]．兰州文理学院学报，2016，30（6）：99-102．

[5] 朱灿，洪丹．基于曲线导数的二元函数微分中值定理[J]．大学数学，2016，32（1）：110-113．

[6] 张辉，敬斌，赵伟舟，等．浅谈方向导数的几何意义[J]．数学学习与研究，2014（19）：105．

[7] 郭建新．谈方向导数与梯度的几何意义[J]．甘肃高师学报，2009，14（5）：17-18．

[8] 李晓丹，纪永强．二元函数方向导数的几何意义[J]．湖州师范学院学报，2009，31（1）：132-134．

[9] 徐助跃．二元函数方向导数的解法及推广[J]．吉林师范大学学报（自然科学版），2011（4）：137-140．

Differential mean-value theorem of space curves

NIU Lina，REBIGULI Tuniyazi

（School of Science，Xinjiang Institute of Technology，Akesu 843100，China）

space curve；tangent vector；directional derivative；differentiable；differential mean-value theorem

1007-9831（2022）10-0006-04

O174.55

A

10.3969/j.issn.1007-9831.2022.10.002

2022-03-12

国家自然科学基金项目（11861061）；新疆理工学院校级教改项目（PT-2022020）

牛丽娜（1990-），女，新疆温宿人，讲师，硕士，从事常微分方程研究．E-mail：156513306@qq.com