精密三角高程测量在跨河高程传递中的应用

黄赟，王灵犀，李创

(重庆市勘测院，重庆 401120)

1 引 言

对于河谷等地形起伏大、地貌多变、环境复杂的区域，工程项目的勘察、施工、监测具有较大困难，尤其是对于高程的传递。传统几何水准法往往存在受环境和地形因素影响大、观测距离受限、作业效率低、施测过程复杂等缺点，而三角高程测量方法受地形制约少、观测距离较长、施测简便快速，尤其适用于长距离、大跨度、大高差条件下的高程传递[1～3]，其基本原理是通过观测已知高程点到目标点的竖直角和水平距离来计算两点间的高差，主要误差项包括：距离和角度测量误差、仪器高和觇标高量取误差、大气折光和地球曲率的影响。随着测量机器人和测绘新技术的发展，精密三角高程测量法可满足二等水准的规范要求[4，5]。

本文利用两台高精度测量机器人同时对向观测高低棱镜组的方式，大幅减弱了大气折光、仪器高量取误差、垂线偏差及地球曲率对测量精度的影响。结合重庆某轨道交通工程项目，介绍了精密三角高程测量在跨河高程传递中的主要方法和措施，并分析了观测成果的质量，结果表明，该方法显著提高了测量效率，降低了作业强度，且成果精度能够满足二等水准的规范要求，应用效果良好，对该类工程具有一定的借鉴意义。

2 精密三角高程测量方法

2.1 观测程序

选用两台精度相当的测量机器人，一台标记为主站，另一台标记为辅站，并对仪器加装高低棱镜模拟往返观测[6]，如图1所示。

如图2所示，在水准线路AB的两点间架设Z1到Zn(n为奇数)临时测站作为转点，观测步骤如下：

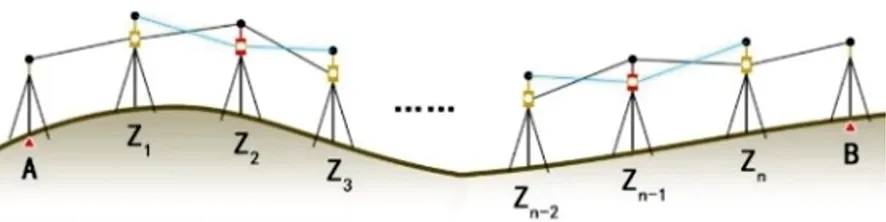
图2 水准线路图

①将强制对中杆架设在起始点A处(对中杆高度固定，在终点B上架设时保持不变)，将主站架设在Z1点处，将辅站架设在Z2点处，并将主站的高低棱镜安装到对中杆上；

②首先主站观测A点处的高低棱镜，得到斜距S和竖直角α，求得高差hz1A，完毕后将棱镜安装到主站上；

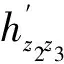
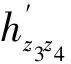
⑥将强制对中杆架设在B点处，将主站的高低棱镜安装到对中杆上，由Zn点处主站观测B点处高低棱镜，求得hznB，完成线路AB的观测。

2.2 基本原理

点Zi-1和点Zi间的高差取两点间往返测高差中数，计算点A和点B间的高差如下：

(1)

hAB=-hz1A+hz1z2+hzi-1zi…+hzn-1zn+hznB

(2)

假设点Zi处仪器高为iZi，棱镜高为tZi，点A到Z1与点B到Zn间的距离大致相等，且数值较小(10 m左右)，则仪器对点A和点B的单向观测所产生的垂线偏差误差项、大气折光误差项以及地球曲率误差项变得微乎其微，在此可忽略不计；同时，转点间的对向观测将大幅削弱大气折光和垂线偏差的影响，完全消除了地球曲率的影响[7]，则简化后hAB的计算公式[8～11]推导如下：

hz1A=Sz1A×sinαz1A+iz1-tA

(3)

(4)

……

(5)

(6)

hznB=SznB×sinαznB+izn-tB

(7)

(8)

由于点A和点B采用同一副对中杆和棱镜，故tA=tB；由于n为奇数，即转点Z1和Zn处为同一台仪器，有tz1-iz1=tzn-izn，故得：

(9)

由式(9)可知，所求高差和仪器高、目标高无关，消除了人为量高的误差，其精度只与距离和竖直角的观测精度有关，通过采用高精度仪器可显著提高观测结果的精度。

2.3 观测方案

对于跨越河流的高程传递，则按图3所示的大地四边形布设跨河水准点[12，13]，观测线路AB、AD、AC、BC、CD、BD共6条边，其中AC、AD、BC、BD为跨河边。

图3 跨河水准网形

以跨河边AC的观测为例，则按图4所示的水准线路进行布点和观测。为了保证偶数条对向观测边，在水准点A、C之间选定1、2、3三个转点作为仪器设站点，其中点1、点3安设主站仪器，点2安设辅站仪器，边A-1和边C-3的距离限制为 10 m～20 m，边1-2和边2-3为对向观测边，为了保证观测质量，点1、2间要求通视良好，且视线高出水面 10 m以上。

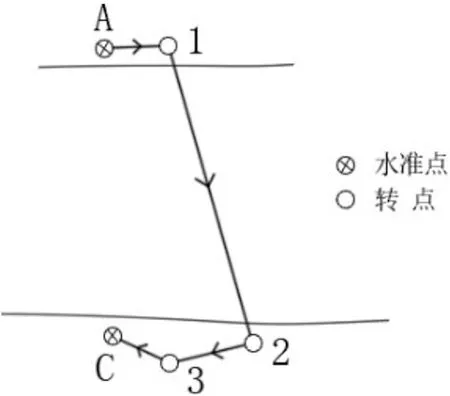
图4 跨河观测线路图

完成线路AC的观测需要辅站和主站各跨河搬站1次，共计2次过河。若采用水准法，则跨河观测线路过长，将大幅提高施测的难度及项目周期，数据质量在一定程度上也会降低；若采用传统三角高程跨河观测法，根据规范要求[15]，观测程序较为复杂，且各观测边均受到大气折光的影响；精密三角高程测量方法则简化了观测流程和程序，且通过两台仪器对向观测的方式，根据2.2相关理论，可大幅消除大气折光的影响。

3 工程应用案例

本文以重庆轨道交通“高家花园大桥跨河高程控制网建设”工程为例开展应用。重庆位于中国西南和长江上游地区，地貌以丘陵、山地为主，区域内山区河流众多，岸坡陡峭、高差起伏大。选用合适的水准测量方法在峡谷、沟壑两岸建立高精度高程基准，是轨道交通工程建设中的关键工作。

3.1 工程概况

高家花园大桥是连接重庆沙坪坝区和江北区的轨道专用桥梁，横跨嘉陵江，全长 594 m，宽 19.6 m，主跨 340 m，是国内最大跨径的轨道专用斜拉桥。根据《城市轨道交通工程测量规范》[14]，水准测量精度应不低于二等水准的规范要求，若采用常规水准测量方法进行高程传递，河两岸相隔不到 600 m的水准点需要单边绕行观测 6 km的水准路线才能完成，长距离测量增加了作业强度和成本，同时多测站又降低了高程传递的精度。本文采用改进的精密三角高程测量法，水准路线长度仅 600 m左右，同时降低了跨河搬站的次数。

3.2 场地选定与点位布设

具体布设如图5所示，其中BM01、BM02、BM03和BM04均为顶端椭球并带有强制对中标志的固定点。由于跨河水准测量边较长，且水面上方空气层与地面不同，使得大气折光差及地球曲率的影响显著增大，为尽可能减弱上述误差的影响，跨河点位的选择及布设应遵循如下原则：

图5 跨河水准测量的网形图

①应选用测线上下游附近较窄河段处，且利于布设水准网和开展观测；

③在两岸处应保证仪器与水边的距离大体相等，其周围地形地貌不应有较大差异，仪器应架设在开阔、通风之处；

④跨河视线方向应避免正对阳光。

3.3 仪器选用

由式(9)可知，测量的精度取决于距离和角度观测的精度，本次选用的两台仪器为徕卡的TM30测量机器人，测角精度为±0.5″，测距精度为±(0.6 mm+1×10-6D)，其中一台作为主站，另一台作为辅站，如图6所示加装高低棱镜，模拟往返观测进行互相校核。

图6 TM30测量机器人

3.4 观测方法

采用改进的精密三角高程测量法施测，以BM01-BM04为例，详细介绍其观测顺序：

①将主站设在靠近BM01处的点A，将辅站设在靠近BM04处的点B，由于BM01-A和B-BM04为单向观测，为降低观测误差，A点和BM01及B点和BM04的距离应大致相等，且限制为 10 m～20 m；

②在BM01处安设强制对中杆，将主站高低棱镜安装到对中杆上，A点处仪器依次观测BM01处高低棱镜；

③A点仪器不动，将对中杆上的高低棱镜安设到A点仪器上，A点和B点处仪器依次进行对向观测高低棱镜；

④B点仪器不动，将对中杆及A点高低棱镜一起搬移至BM04点上，B点处仪器观测BM04处高低棱镜。

按上述步骤依次完成其他3条跨河边的观测，同岸水准点由于距离较近，其高差可采用几何水准测量的方法直接测定。

3.5 成果分析

(1)限差分析

根据二等水准的规范要求，每条边各测回间高差互差应不大于式(10)计算的限值。

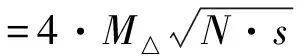
(10)

式中，dH限为测回间高差互查限值(单位：mm)；M△为每千米水准测量的偶然中误差限值(单位：mm)，二等水准规范[15]中M△=1 mm；N为总测回数；s为跨河视线长度(单位：km)。

根据各条边观测所得高差计算由大地四边形组成的三个独立闭合环的闭合差W，应不大于式(11)计算的限值。

(11)

式中，MW为每千米水准测量的全中误差限值(单位：mm)，二等水准规范[15]中MW=2 mm；s为跨河视线长度(单位：km)。

在本项目中，水准网形中的跨河边长度在 500 m～600 m之间，故每条跨河边高低棱镜各观测8个测回，即N=8，取s=0.5 km，计算可得dH限=8.0 mm，W=8.5 mm。以低棱镜观测作为往测，高棱镜观测作为返测，经观测后各测段高差值及独立闭合环的闭合差统计结果分别如表1、表2所示。

表1 测段高差统计结果

表2 闭合差统计结果

由表2可看出，环闭合差最大值为 3.4 mm≤W=8.5 mm，满足二等水准的规范要求。

(2)平差计算

以观测距离定权，对水准网进行平差计算。经计算，每公里水准测量的偶然中误差为M△=0.56 mm≤1 mm，每公里水准测量全中误差MW=1.39 mm≤2 mm，均满足二等水准的规范要求。

4 结 论

本文详细介绍了精密三角高程测量的理论、观测流程和方法，利用两台高精度测量机器人进行对向观测高低棱镜组开展精密三角高程跨河水准测量，通过在重庆某轨道交通跨河水准测量工程中进行应用，结果表明，该方法具有受地形条件影响较小、作业效率高、成果精度满足二等水准的规范要求等优势，尤其对长距离、大跨度等复杂地形下的工程项目具有一定的借鉴意义。