固定式倾角传感器在深层水平位移测量中应用关键技术研究

徐郁峰， 李一鸣， 柯宇

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.华南理工大学 建筑设计研究院有限公司，广东 广州 510640)

基坑测斜是指利用测斜仪观测土体内部的水平位移，一般用于挡土墙变形监测、深基坑边坡监测等，针对不同的边坡变形形式，测斜仪均能够测量其水平位移[1-2]。测斜仪是一种测定钻孔倾角和方位角的原位监测仪器，现有的测斜仪分为便携式和固定式两种，在实际工程现场，应用最广的是便携式测斜仪。

便携式测斜法使用数字垂直活动测斜仪探头，测斜仪上安装有滑轮装置，可以通过控制电缆来控制测斜仪的位置，配合读数仪可以观测测斜管的变形。测量时，先将探头下放到测斜管底部，然后通过电缆将探头从测斜管底部拉向顶部移动，每向上0.5 m进行一次测量角度的工作[3-4]。通过测量角度可以转换为水平位移。对比初始位置可以得到水平位移的变化量。便携式测斜法数据采集过程需要人工拉升传感器，耗时较多，人力时间成本较高的问题比较突出。

固定式测斜法是把传感器用连接杆串联安装后放置在测斜管内的固定高度处[5]，由于传感器位置固定，因此可实现自动化采集，从而大大减少便携式测斜法采集过程人力成本较高的问题。但是由于测斜传感器单价较高，如单孔中的传感器仍参照便携式测斜法的0.5 m一个测点的间距来布置，对深度超过10 m深基坑，单孔需要布置的传感器数量多，导致单孔传感器成本非常高，影响了该方法的推广应用。

增大传感器的布置间距可有效降低成本，目前实际工程应用中一般取1～3 m，但该间距是否合适缺乏理论依据，同样影响了该方法的推广应用。

该文介绍倾角传感器的误差分析方法，包括分段误差和测角误差，得到满足一定测量精度下的固定式倾角传感器的测点布置规律，为深层水平位移的测点布置方案提供理论指导，并在试验室设计试验，以验证该方法的可行性。

1 倾角传感器测量变形原理

Δωi=L1tanθi

(1)

则第i节段末端处挠度为前i-1段所有分段挠度的累积，即：

(2)

式中：L1为每节段的长度；θi为第i节段中点处倾角变化值即该节段倾角传感器测量值；Δωi为第i节段前后端挠度差；ωi为第i节段末端挠度值。

通过测量倾角计算挠度是一种间接的方法，而通过不同的数学模型计算挠度都是近似结果，即不是准确的挠度值[6-7]。倾角传感器测量变形原理见图1。

图1 倾角传感器测量变形原理图

2 固定式倾角传感器测量变形误差分析方法

利用倾角传感器测量基坑变形是一种间接测量方法，首先要对由分段直线代替曲线产生的误差进行分析，然后需要考虑倾角传感器本身的测量精度。通过考虑倾角传感器的分段误差以及测角误差，即可完成倾角传感器选型。

基坑的形式多种多样，实际工程中，需要对基坑开挖过程进行深层水平位移的测量，由于基坑的种类繁多，并且基坑的深度深浅不一，根据深基坑及浅基坑的分类，选取不同基坑深度进行分析。因此，针对不同深度基坑(5、15、25 m)开挖过程(开挖1/4、开挖1/2、开挖3/4、开挖完)中的变形，确定倾角传感器的布置方案。

2.1 基坑变形曲线

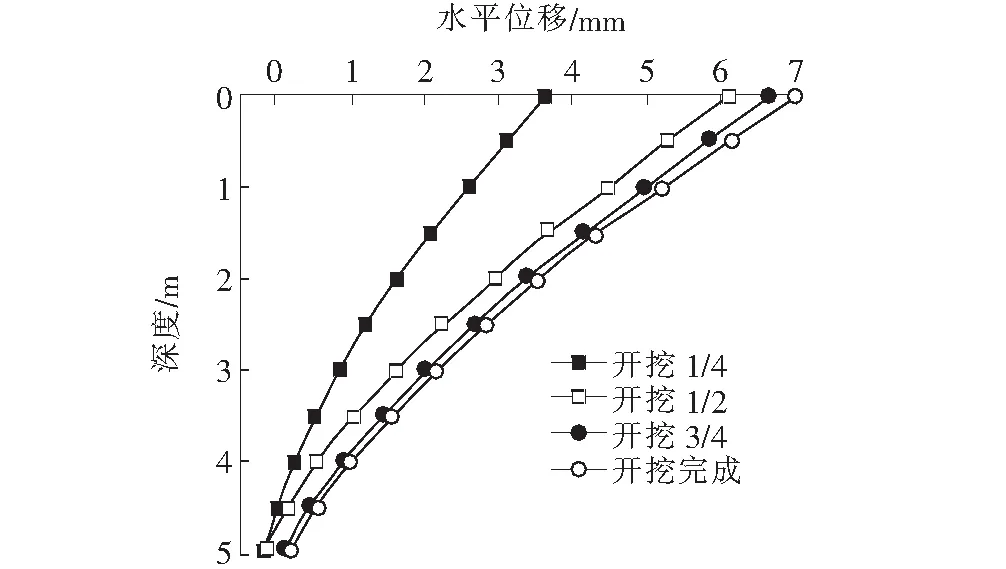
对不同深度基坑的开挖过程进行模拟，采用Midas GTS软件分别建立5、15、25 m基坑开挖二维模型。根据模型，得到不同深度基坑不同开挖过程中，基坑地下连续墙的理论水平位移，如图2所示。

由图2可以看出：5 m基坑变形曲线为一条无“拐点”的曲线。15 m和25 m基坑的理论变形曲线均存在一个“拐点”。

(a) 5 m

基坑深层水平位移，一般是连续光滑的曲线，且曲线次数不会太高，因此可采用多项式函数进行拟合。5 m基坑的变形曲线采用二次函数拟合，15、25 m基坑不同开挖过程均采用四次函数拟合。

2.2 分段误差分析

利用倾角传感器测量变形，需要将角度转化为位移。首先需要将基坑按照深度进行分段，倾角传感器布置在每一段的中间点，将倾角传感器所测角度乘以分段长度，即可得到该段的变形，采用分段叠加法，将每一段的变形进行叠加，即可得到每一点的累计变形。

进行分段误差分析，首先需要确定分段数，一般来说，分段数大于等于多项式次数时，分段误差能得到比较好的控制[7]。对于变形曲线上的每条连续光滑的单圆弧，至少应安装两个倾角传感器[8]。

进行分段误差分析时，需要得到变形计算的计算值和理论值。计算值利用分段叠加法得到，理论值通过将某一点的坐标代入理论变形曲线中计算得到，通过比较两者的误差，即可判断分段数对误差的影响。

5 m基坑变形曲线均用二次函数拟合，因此分段数为2、3段。15、25 m基坑不同开挖过程均采用四次函数拟合，分段数为4、5、6段和4、5段。

以25 m基坑开挖1/4工况为例进行分析，利用Matlab进行多项式拟合得到函数为：

y=-0.000 144x4+0.008 326x3-0.120 5x2+0.071 83x-0.205

(3)

式中:x为由基坑底部往上的距离；y为某一点的水平位移。

拟合函数为四次函数，因此分段数取4、5段，对式(3)求导，可得：

y′=-0.000 576x3+0.024 978x2-0.241x+0.071 83

(4)

分段数为4时，每段长度为6.25 m，每个倾角传感器位于每一段的中间，因此可以得到倾角传感器的位置，将位置距离代入式(4)即可得到该处的倾角正弦值，倾角正弦值乘以分段长度，并由基坑底部往上叠加，即得到挠度计算值。同时将每段的末端坐标代入式(3)，即可得到挠度理论值，将基坑中间点的计算值与理论值进行对比。分析过程及结果如表1所示。其他工况及分段数均按表1及上述步骤进行分析。

表1 分段误差分析过程

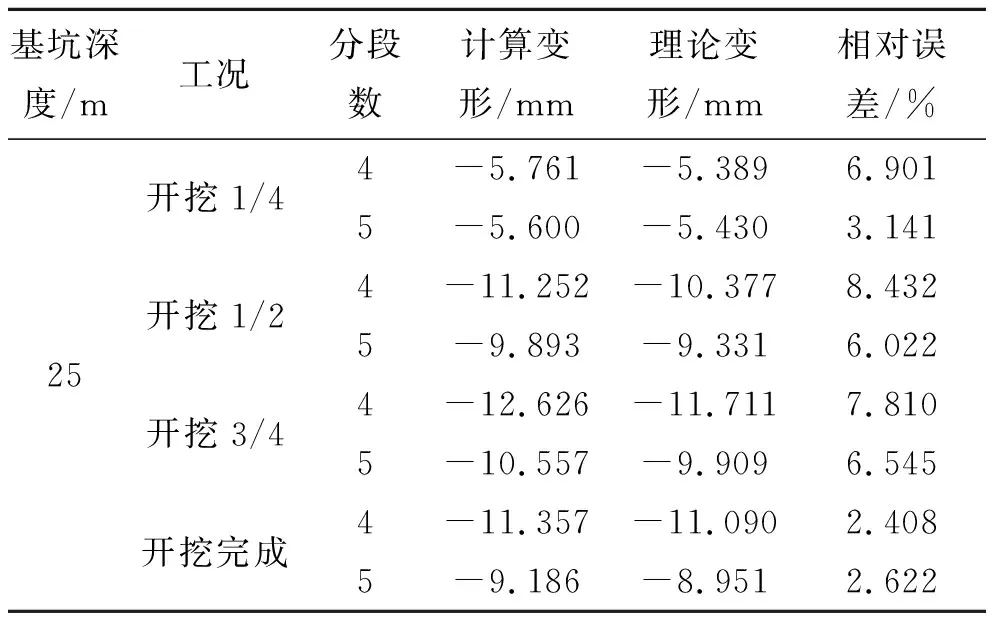
5、15、25 m基坑分段误差分析结果如表2所示。

表2 分段误差分析结果

续表2

由表2可以看出：随着分段数的增加，相对误差不断减小，当分段数为4段时，虽然相对误差最大达到8%左右，但比较计算变形以及理论变形可以发现，5 m基坑的最大绝对误差为0.295 mm，15 m基坑的最大绝对误差为0.502 mm，25 m基坑的最大绝对误差为0.915 mm。考虑到绝对误差较小，因此5 m基坑分段数至少采用2段。15 m和25 m基坑分段数至少采用4段。

2.3 测角误差分析

倾角传感器的误差包括灵敏度误差、零点偏置等系统误差以及输入轴非对准性等随机误差[9]。倾角传感器的测量精度需要将系统误差和随机误差进行组合。倾角传感器测量值的分布是一个符合以倾角真值为均值(数学期望)，以各项精度影响因素的标准差平方和为方差的正态分布[6]。

采用蒙特卡罗法进行不确定度的评定，选取测量精度为0.01°和0.001°的倾角传感器，对每一个倾角传感器的测角误差进行分析，取蒙特卡罗系数M=1 000，对各个倾角传感器进行1 000次随机取值，并作1 000次挠度的模拟测量。

以25 m基坑开挖1/4的分段数为4、测量精度为0.01°进行说明，因此4个倾角传感器测量值的分布规律如下，从基坑底部往上分别为1#～4#倾角传感器。

θm1～N(-24.463,0.012)、θm2～N(-25.024,0.012)、θm3～N(11.700,0.012)、θm4～N(35.868,0.012)

采用蒙特卡罗法进行分析，对4个传感器进行1 000次随机取值，根据分段叠加进行1 000次挠度模拟测量，经过统计分析，结果如表3所示，95%概率相对误差结果如表4所示。

表3 测角误差分析内容

由表4可以看出：当传感器数量即分段数不变时，变形测量的误差与传感器精度成反比，精度越高，误差越小。

2.4 固定式倾角传感器布设方案

综合分段误差及测角误差分析结果，5 m基坑至少采用2个精度为0.01°的倾角传感器。15 m和25 m基坑均至少采用4个精度为0.01°的倾角传感器。

因此，当5 m基坑理论变形曲线无“拐点”时推荐至少采用2个精度为0.01°的倾角传感器，若理论变形曲线出现1个“拐点”，则推荐至少采用4个精度为0.01°的倾角传感器。15 m和25 m基坑理论变形曲线均出现1个“拐点”，推荐至少采用4个精度为0.01°的倾角传感器。在工程实际中，需根据基坑变形曲线确定合理以及经济的倾角传感器布置方案。

3 固定式倾角传感器变形测量对比试验

3.1 固定式倾角传感器变形测量对比试验方案

在试验室设计对比试验，将测斜管分为5段，在每段中间安装倾角传感器，并在每段的顶部安装一个百分表，通过人工主动调节对结构施加变形，测试在不同调节工况下两者的数据，利用倾角法计算得到变形值并与百分表测量的变形值进行对比，即可判断该方法的可行性。试验室验证装置整体图如图3所示。

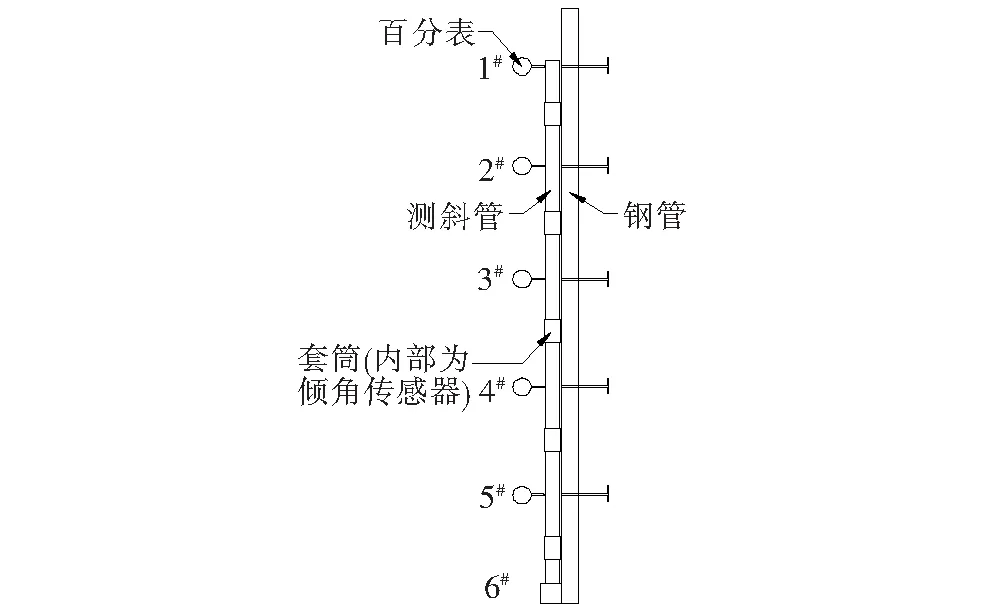
图3 测斜管整体图

3.2 测斜管及固定式倾角传感器的安装工艺

试验室所需仪器设备如表5所示。

表5 试验室仪器汇总

所设计倾角传感器的直径等于套筒的内径，且倾角传感器外壳上设置4处凸起的卡槽。测斜管及套筒为PVC管，在套筒上设计了4处凹槽，因此可以将倾角传感器根据卡槽卡入套筒的中部。起到固定倾角传感器位置的作用。

将套筒卡在测斜管上，倾角传感器、套筒、测斜管之间用云石胶进行密封加固处理，倾角传感器之间采用数据连接线串联的方式进行连接，连接线放置于测斜管内部，可以避免出现线路纠缠的情况。

将各段连接完毕的测斜管焊接于钢管上，将长螺栓安装于钢管上。钢管上的倾角传感器安装位置预先开螺栓孔，施加变形时，利用螺栓往外顶测斜管，从而施加变形，在测斜管上安装5个百分表，根据百分表的读数控制施加变形的大小，并将百分表的读数与倾角传感器数据进行对比。

3.3 对比试验工况

测试过程中，为了较好地对比百分表与倾角传感器所测量数据，设计6个测试工况。各工况详细情况如下：

(1) 工况1：在5#位置利用螺栓对测斜管施加3 mm的变形，使百分表读数为3 mm。

(2) 工况2：在工况1的基础上，使4#位置的百分表读数为3 mm。

(3) 工况3：在工况2的基础上，使3#位置的百分表读数为3 mm。

(4) 工况4：在工况3的基础上，使2#位置的百分表读数为3 mm。

(5) 工况5：在工况4的基础上，使1#位置的百分表读数为3 mm。

(6) 工况6：使3#位置的百分表读数为5 mm。

待结构稳定后，在不施加任何变形的情况下，进行数据采集，将采集的数据作为初值。然后分别按工况1～6施加变形，并待结构稳定后分别读取百分表和采集倾角传感器的数据。

根据倾角计算挠度的原理，将测斜管分为5段，每段长度为1.0 m，将所测倾角值减去初值的正切值乘以分段长度，即可得到该段的挠度变化量，通过由下往上分段叠加即可得到每个测点的挠度值。

3.4 对比试验结果

试验数据如表6所示，不同工况不同位置处水平位移如图4～6所示。

表6 试验室数据汇总

由图4～6可以看出：倾角传感器所测挠度值与百分表挠度值趋势基本一致且误差较小，最大误差出现在工况1的测点4#，百分表与倾角传感器所测挠度误差为0.15 mm，出现误差的原因可能是，测斜管顶部与钢管的连接不牢固，同时倾角传感器所测倾角利用分段叠加法转换为挠度存在误差。

图4 工况1、2对比图

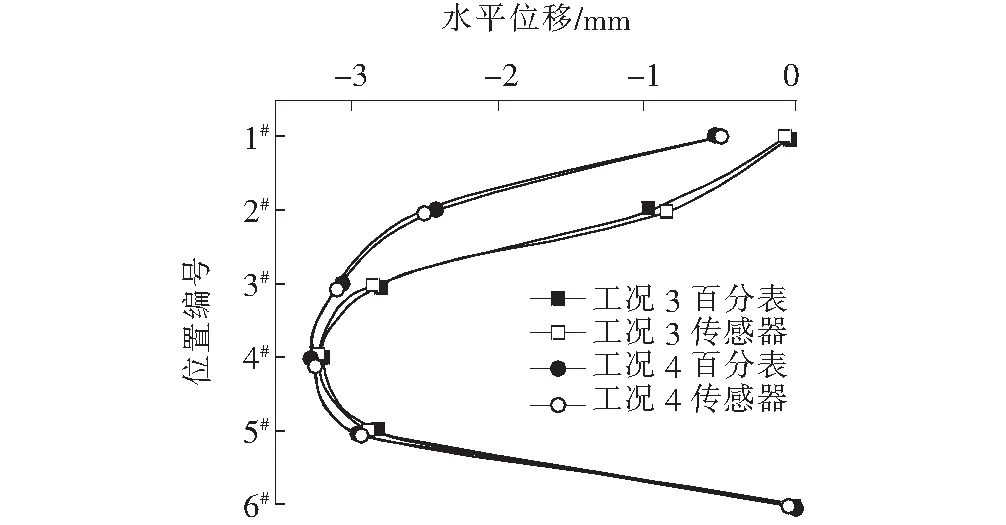
图5 工况3、4对比图

图6 工况5、6对比图

试验室对比试验表明：采用该文方法布设固定式倾角传感器所测量的深层水平位移与真实位移之间的误差能满足工程测量精度要求。

4 结论

(1) 倾角传感器测量变形的分段误差及测角误差的分析方法能够为深层水平位移测点布置提供理论指导，解决了便携式测斜法和固定式测斜法缺乏理论指导的问题。

(2) 当传感器数量即分段数不变时，挠度的测量误差会随着传感器精度的提高而减小，大多数情况下，当分段数大于或等于多项式次数时，分段相对误差可以控制在较小的范围内，随着分段数的增加，分段误差逐渐减小。增加分段数有利于提高测量精度，但考虑到合理性及经济性，传感器的数量不能盲目增加，需根据实际变形曲线确定合理及经济的布置方案。

(3) 通过测角误差和分段误差的分析，得到了一定测量精度下固定式倾角传感器测点布置的规律，即 5 m基坑理论变形曲线没有“拐点”时推荐至少采用2个精度为0.01°的倾角传感器，若理论变形曲线出现“拐点”时，推荐至少采用4个精度为0.01°的倾角传感器。15 m和25 m基坑理论变形曲线出现1个“拐点”，推荐至少采用4个精度为0.01°的倾角传感器。

(4) 通过固定式倾角传感器室内对比试验，采用该文所述布设固定式倾角传感器的方法与真实位移之间的误差能够满足实际工程测量的精度需求。

(5) 该文所述误差分析方法及测点布置规律可对固定式倾角传感器测量深层水平位移提供理论指导，可以取代传统的手持式测斜仪以及固定式测斜仪，并且可以通过布置少量的倾角传感器达到高精度测试的目的，具有实际推广意义。