导管注浆导管-浆土界面拉拔力学性能研究

许杨少君， 周勇， 容洪流*， 潘彦邑， 钟贤勍

(1.广西大学 土木建筑工程学院， 广西 南宁 530004； 2.中国建筑第八工程局有限公司南方公司， 广东 深圳 518100)

导管注浆加固技术作为一种普遍用于隧道、边坡进行施工防护和加固的技术，它的发端可追溯到20世纪50年代出现的小直径桩(微型桩)支护技术[1]。其主要是在不对岩土体进行较大规模开挖的前提下，通过浆液的凝结将导管与土组合成一个整体，根据导管布设和埋深的不同，可形成锚、抗滑桩、群桩、挡土墙等支护结构作用[2-3]。

针对边坡失稳以及隧道内土体滑动这种存在土石方量大，滑动作用时间短等特点的工程问题，使用导管注浆具有施工方便、加固效果明显以及轻型化、小型化等优点[4]，因此导管注浆加固技术长期以来备受岩土工程领域学者及相关工程人员的重视。近年来，诸多国内外学者专家基于导管灌注施工方法，研究导管注浆在处治边坡、隧道失稳及施工加固的作用机理及效果，取得了诸多有益的成果[5]。

在对边坡采用加固措施时，对于加固措施参数的优化十分重要。研究表明：在使用优化过重要参数的锚索支护下，边坡的安全系数提高了近一半[6]。对于采用有相似加固作用的导管注浆对边坡进行加固时，其设计重点主要在于注浆后的加固土性质和导管锚固力的计算，但现行的设计多依靠经验，缺乏理论依据。故需要对导管注浆工程进行更加合理的设计计算以及提供更为明确的理论依据，对于重点的注浆导管的锚固力设计可以根据其自身的特点分为两个部分进行分析：一是导管与注浆土的黏结强度[7]；二是依赖于导管与土体的变形协调所产生的轴力。

研究针对锚固力设计中的导管与注浆土的黏结强度这一部分，通过导管拉拔试验研究浆液水灰比和锚固长度两个因素对黏结强度的影响；并通过对导管拉拔过程进行数值模拟研究锚固体及周围土体受力和位移情况的变化规律；并建立锚固体与周围土体之间的界面力学本构关系。通过试验结果与理论计算的对比得到导管-浆土黏结强度的合理精确分析方法，为注浆导管锚固力的设计提供依据。

1 导管注浆的锚固效应与加固力作用下的边坡稳定计算原理

1.1 导管注浆的锚固效应

导管注浆加固边坡的基本作用原理是：采用带有小孔的小直径钢管，插入需要加固的边坡岩土体中，采用一定的压力向导管中注入加固浆液，在压力作用下，浆液经由小孔向土层喷射，注入岩土中，将岩土固结，形成注浆锚固复合加固体。导管注浆主要通过注浆固结效应以及注浆导管的锚固效应对边坡进行综合加固。注浆导管的锚固效应如下：插入岩土体的小导管按锚杆进行布置时，完成注浆作业后的小导管与浆土通过黏结作用形成整体，边坡岩土发生变形时，应力通过导管与固结岩土体界面传递，此时小导管对边坡起到锚固作用。由于小导管与注浆体形成为一个整体，其直径较锚杆大，锚固作用十分明显，并能够承受边坡下滑所产生的剪切应力；由于注浆导管浆液扩散所形成的导管-浆土的整体影响范围较锚杆更大，因此导管注浆施工对导管的方向性及黏结锚固要求可适当降低。

1.2 加固力作用下的边坡稳定计算原理

对于加固力作用下的边坡稳定计算，目前有很多研究[8]，而使用传统的极限平衡条分法进行分析时，通常将边坡的加固方式简化为一个或多个加固力作用在坡体上。当注浆导管与水平方向呈某个角度贯入时，其加固力可以按锚固力分析，Zornberg等通过离心机试验表明：将加固力作为已知力，通过极限平衡分析法对加固力的作用方式及大小进行模拟试验，再根据试验结果对加固力进行反复调整以满足安全系数的设计需要。在极限平衡原理的基础上，考虑加固力作用的安全系数Fs可表示为：

(1)

式中：F′为已知加固力；TS为平衡所需的剪应力；Tf为土体抗剪强度。

式(1)中的加固力并未考虑强度折减的影响，实际边坡设计中，加固力应作为长期作用力考虑，并通过人工结构物才能发挥效用。如图1所示的锚杆加固边坡时，加固力F′在设计时需考虑：① 抗拉强度；② 徐变特性；③ 安装损坏；④ 锚杆耐久性；⑤ 拉拔抗力；⑥ 边坡内加固体的刚度及允许变形等因素影响。

图1 锚杆固坡原理

根据图1，考虑边坡锚固力时的安全系数Fs以及锚固力T的计算表达式为：

(2)

(3)

式中：Fs为边坡安全系数；[Fs]为安全系数容许值；T为锚固力；c为滑动面的黏聚力；φ为滑动面的内摩擦角；W为滑动土体自重；L为滑动面长度；U1为滑动土体底面孔隙水压力；U2为张拉裂隙中的水压力；δ为锚杆与水平面夹角；β为滑动面倾角。

1.3 使用传统加固力作用下的边坡稳定计算方式计算注浆导管锚固力存在的问题

在使用导管注浆作为边坡加固措施时，考虑如图1所示的坡体失稳状态，在采用刚体极限平衡方法计算导管锚固边坡的稳定性时[9]，会出现设计锚固承载力的增大与计算所得的边坡安全系数增大关联性不如预期的情况，即锚固力在设计上即使大幅增大，其对边坡安全系数的贡献仍然有限，与实际工程情况不符。这主要是因为锚杆所施加的加固力在边坡破裂面上对土体有明显约束挤压效应，相应提高了滑动面土体的黏聚力以及弹性模量，并在计算中低估了锚固力沿破裂面切向分力对土体抗滑的贡献。通常锚杆注浆体位于锚杆端部，位置较边坡破裂面更深，实际破裂面出现时，锚固作用下破裂面上的土体力学参数如何变化，目前在设计上并未有较详细的考虑与规范。锚固力对土体性质具有一定的影响，在加固设计时应给予重视。综上可知：注浆导管锚固力与传统的锚杆锚固力的设计计算不尽相同，所以需要对注浆导管锚固力进行更为合理和精确的分析。

2 导管-浆土界面拉拔力学性能试验研究

2.1 注浆导管拉拔试验设计

导管埋入土层后注浆，使导管周围在浆液扩散半径内形成浆土固结体，导管本身可以起到锚杆锚固作用，因此注浆导管需进行锚固力的拉拔测试试验，明确浆液水灰比，锚固长度[10-11]这两个影响黏结强度的重要因素对其的影响程度。试验设计为：

(1) 浆液采用标号为P32.5的水泥浆液。

(2) 试验模具内预埋直径60 mm塑料管后夯实周围土层，取出塑料管后填充经拌和后的浆土混合体，然后迅速埋入直径22 mm的注浆导管。

(3) 静置养护28 d后，进行拉拔试验测试。

(4) 测试内容：对以水灰比为变量的试验组分级加载，直到拉拔力不随导管位移的增加而增加之后停止加载，记录每级荷载与其对应的导管位移值；对以锚固长度为变量的试验组分级加载，直到荷载达到设计最大荷载时，停止加载，记录每级荷载与其对应的导管位移值，并测量最大导管拔出量、回弹量。

具体试验设计方案如表1所示。试验采用如图2所示HC-20手动拉拔仪进行加载拉拔，千分表在导管顶部装置测量拉拔过程中的位移变化。根据《岩土锚固技术手册》及《土层锚杆设计与施工规范》中相关理论与规定，加载方式为分级加载，每级加载读数3次，读数稳定后，持续5 min再施加下一级荷载。

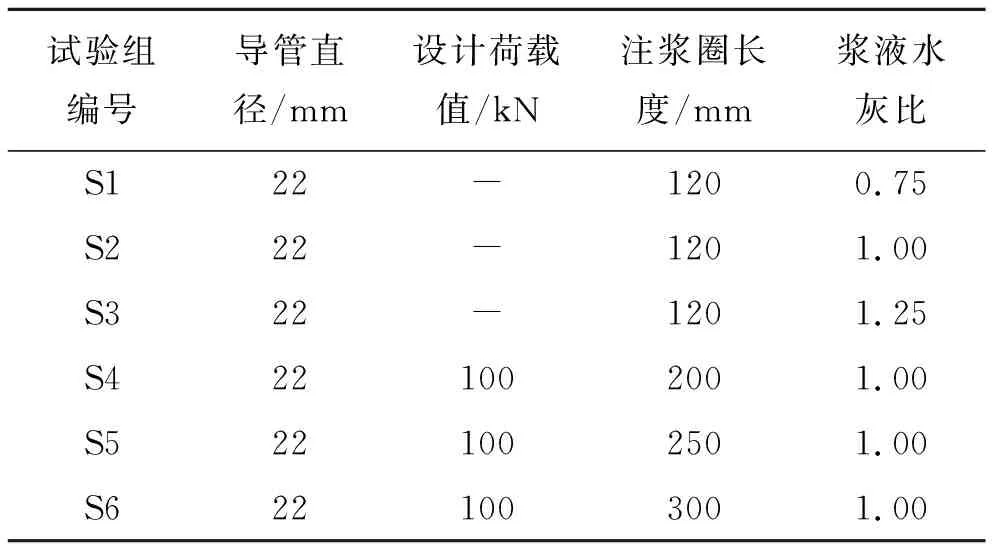
表1 拉拔试验设计

图2 拉拔试验设备

对照试验组S1～S3，其试验目的在于研究分析浆液水灰比对锚固效果的影响。试验不设置目标加载值，每次分级加载值较前次增加约5 kN。

对照试验组S4～S6，其试验目的在于研究分析锚固长度对锚固效果的影响，对于导管注浆形成的锚固效应，将注浆后注浆圈沿导管径向的包裹长度作为锚固长度，实际工程中，该长度为导管径向注浆小孔的分布范围。试验需设置目标加载值，按最大容许试验荷载法，最大试验荷载为锚杆设计轴向拉力值的1.5倍，可根据前3组试验结果数据，得到试验组S4、S5、S6设计最大加载值为100 kN。分8级加载，分级加载设计依次为：15、30、50、60、70、80、90、100 kN。试验直至加载达到最大设计荷载为止。

2.2 拉拔试验结果分析

对照试验组S1、S2、S3导管-浆土锚固体的拉拔力-位移关系如图3所示。可知锚固力在加载初期变化趋势较为一致，水灰比为1.25的试验组S3最先出现峰值点，试验组S2与S1峰值点依次出现；根据试验结果可知：水灰比越低，导管与浆土的黏结锚固作用力越大，表明浆体的性能对导管与土体间的界面力学性能有重要影响。

图3 不同水灰比注浆导管拉拔试验结果

观察分析对照组S1、S2、S3各自的P-s曲线(轴力-位移曲线)峰值后的曲线变化趋势，S1和S2曲线在峰值点后的曲线斜率明显较S3的斜率小，锚杆锚固的力学原理为刚性锚杆与浆土或土层间的界面剪切行为，由于水泥浆液对土体颗粒的固结作用，使得试验中导管与浆土间的结合方式以黏结为主，当拉拔力增大至足以破坏导管与浆土界面的黏结作用时，两者间的咬合及摩擦作用仍在一定程度上阻止了导管与浆土间相对位移的发生，同理作用在浆土与土层的界面上。

因此，低水灰比的浆液对松散土颗粒的固结效果更好，即使导管—浆土—土层间黏结已被破坏，但已经固结成块的浆土仍具有较好的摩阻作用。

对照试验组S4、S5、S6导管-浆土锚固体的拉拔试验结果如表2及图4所示。

表2 拉拔试验结果

图4 注浆导管拉拔P-s曲线图

根据表2可知:注浆圈径向长度对于导管拉拔强度影响明显，试验组S4最终加载峰值为87.63 kN，后一级加载时的P-s曲线已呈下降趋势，卸载导管回弹率为21.58%，如图4(a)所示；试验组S5最终加载峰值为95.50 kN，由图4(b)所示的P-s曲线可知，荷载峰值点后曲线上升趋势放缓，是否已达到最大临界承载值尚不明确，卸载后导管回弹率为52.60%；试验组S6最终加载值为103.34 kN，由图4(c)所示P-s曲线可知，试验组S6加载过程较接近线弹性状态，卸载后导管回弹率57.02%，为3组中最高；表明锚固深度越大，导管锚固性稳定，可承载更大的外部荷载。

2.3 拉拔试验数值模拟分析

由于室内试验仅测试了注浆导管与土层间的黏结强度关系，对于拉拔过程中土层内部的土体变形与应力分布未能了解，很多资料显示锚固体应力的分布并不是均匀的[12-13]，因此建立如图5所示的拉拔试验数值模型用以辅助研究。该模型中，浆液扩散区域内土颗粒与导管固结形成锚固体，实际拉拔过程中，破坏往往首先出现在锚固体与土体接触面上，因此试验测定的拉拔力及位移的数值多为锚固体与土体间的相对摩擦力与相对位移。模型参数见表3。

图5 拉拔试验数值模型

表3 边坡模型物理力学性质参数

在拉拔试验基础上，该文通过建立数值模拟模型，研究分析锚固体及其周围土体在拉拔加载过程中的受力与位移变化，后续在此基础上进一步推导研究两者的界面力学模型。

图6为距离导管不同距离土体径向位移变化情况。每个计算时步对应导管拉伸3.2×10-4cm，径向位移的产生是由于土体剪胀效应引起，由于实际试验中，已经人为控制了注浆圈半径为30 cm，因此将距离小于30 cm的土体位移视为锚固体位移。从图6可以看出：锚固体周围土体的径向位移曲线为单峰值曲线，越靠近锚固体的土体径向变形增量越大；导管锚固受拉破坏前，土层内部径向位移较小。

图6 土层径向位移曲线

图7为锚固体与土层剪切应变分布关系与变化曲线图。由图7可以看出：剪应力沿锚固体轴向并非均匀分布，其最大剪应力分布范围靠近近端锚固体，在破坏前，远端锚固体剪切应力较小。同时，根据不同位置剪切应力变化曲线可以看出：锚固体与土层相切的界面是整个拉拔过程中最大剪切应力出现的部位，因此推断：注浆导管锚固力的形成，实质上是导管与浆土共同组成的锚固体，与周围土层摩擦咬合所形成的力，在锚固体与土层交界的一定范围内存在两者共同工作时的最大应力。

图7 锚固体及土层剪应变曲线

3 注浆导管与土层的界面力学本构关系

通过拉拔试验结果分析，导管与土层透过浆液黏结固结成锚固体，拉拔力超两者间的黏结力时，锚固失效。在分析导管注浆拉拔特性时，将浆液扩散半径范围内的浆土作为锚固体，由数值模拟拉拔过程中土体内部的应变与变形可知：土体的力学效应主要分布在距离锚固体很近的范围内，有学者将这一范围内的土体定义为锚固界面层[14]，如图8所示。锚固体轴向受力产生位移时，土层的位移仅发生在界面层内，且界面层内各点位移连续，具有剪胀效应，位移大小由锚固体向土层衰减，因此假定界面层厚度是稳定的。在此基础上可建立注浆导管与土层在拉力作用时的界面力学关系。

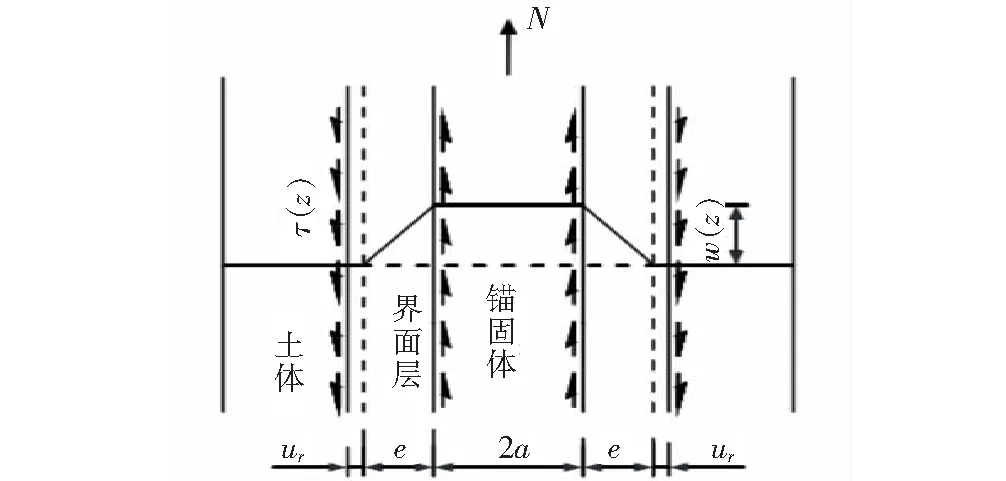
图8 锚固体与界面层分布示意

土作为一种典型的Coulomb材料，满足Coulomb屈服条件相关联的流动法则，Coulomb屈服函数F的表达式为：

F=τ-σntanφ-c=0

(4)

式中：σn、τ为锚固界面层的正应力、剪应力。

再根据塑性位势理论：

(5)

式中：G为界面层内土体的位势函数，土层符合Coulomb屈服法则时，可令G=F，因此可建立界面层内土体应变增量与应力的关系为：

(6)

(7)

(8)

由式(8)可知：当界面土体内摩擦角φ大于0时，界面层具有明显的剪胀性。由图8可知：锚固界面层厚度为e时，令土层的径向位移函数为ur(z)，轴向位移函数为w(z)，则界面层塑性线应变与剪切应变为：

(9)

(10)

假定土层满足理想弹塑性要求，采用Winkler假定研究图8中ur范围内土层的径向变形，则土层正应力表达式为：

σn=kur(z)

(11)

式中：k为土层抗力系数。

将式(11)与式(8)～(10)联立即可得到正应力计算式为：

σn=-0.5kw(z)tanφ

(12)

根据土层锚固的界面力学研究[15-16]，研究如图9所示的锚固单元体，设其单元长度为dz，dN为轴力增量，拉拔试验中为拉拔力沿轴向的增量，当锚固体半径为a时，根据平衡条件，有：

(13)

假定锚固体正常发挥效用时处于弹性阶段，则由胡克定律：

图9 锚固单元体受力分析

(14)

式中：E为锚固体弹性模量，该文为导管与浆土的综合弹性模量(Pa)；A为锚固体横截面积，该文为导管与浆土横截面积和，近似等同于注浆钻孔面积(m2)；w0为整个锚固长度z的位移。

对式(14)的位移z求导两次，得：

(15)

联立式(13)～(15)，令锚固体面积为A=aπ2，则有：

(16)

根据Coulomb屈服条件[式(4)]，可得到锚固体界面位移的微分方程及其通解为：

(17)

(18)

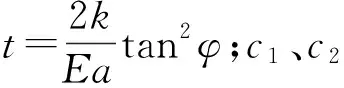
将式(18)代入式(13)、(15)，解出轴向拉力与界面剪切力本构关系为：

N=c1tsh(tz)+c2tch(tz)

(19)

(20)

由式(19)、(20)可知：z=0时，即N为拉拔时施加的拉力；z=L时，即锚固体尾端并无拉力，其受力状态为浆体与导管界面黏结力。

由式(19)、(20)计算试验组S1～S6最大承载力，结果如表4所示。可得S1～S3误差值分别为5.40%、8.04%、1.80%，表明本构理论计算精度良好，可用于锚固设计。

表4 实测值与理论计算结果

4 结论

导管注浆锚固力是导管注浆重要的设计组成部分，根据注浆导管的拉拔试验测定、对拉拔过程的数值模拟以及分析导管浆土界面的力学本构关系，对注浆导管锚固力中的导管与浆土的黏结强度部分进行了全面且完善的分析，所得结论如下：

(1) 注浆导管的锚固效应与锚杆锚固机理一致，但在使用传统的考虑加固力作用下的边坡稳定计算方式时，往往会出现与现实情况不匹配的问题，所以需要对注浆导管的锚固力准确地计算和设计。

(2) 根据注浆导管拉拔试验结果可知，水灰比越低，浆液对松散土颗粒的固结效果越好，导管与浆土的黏结锚固作用力越大，表明浆体的性能对导管与土体间的界面力学性能有重要影响。

(3) 根据注浆导管拉拔试验结果可知，注浆圈径向长度对于导管拉拔强度影响明显，锚固深度越大，导管锚固性稳定，可承载更大的外部荷载。

(4) 通过建立数值模拟分析可知，越靠近锚固体的土体径向变形增量越大，导管锚固受拉破坏前，土层内部径向位移较小。此外剪应力沿锚固体轴向并非均匀分布，其最大剪应力分布范围靠近近端锚固体，在破坏前，远端锚固体剪切应力较小，且整个拉拔过程中最大剪切应力出现的部位为锚固体与土层相切的界面。

(5) 在数值分析基础上建立注浆导管与土层在拉力作用时的界面力学本构关系，得到轴向拉力与界面剪切力本构关系，并通过与拉拔试验结构对比，可知本构理论计算精度良好，可用于锚固设计。