基于附加质量的单点模态振型参数损伤识别研究

孙虎， 狄生奎， 杜祝遥, 王立宪， 项长生

(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室， 甘肃 兰州 730050； 2.陕西国防工业职业技术学院， 陕西 西安 710302；3.西部土木工程防灾减灾教育部工程研究中心， 甘肃 兰州 730050)

近年来，利用梁结构动态响应中的动力特性数据来识别损伤，具有坚实的理论依据与广泛的应用价值[1-3]。在此基础上，已有多种方法[4]提出并初步应用到实践中。但是，这些方法在实践中还有许多问题需要完善，如测量精度、误差以及测量数据的不完整性，对于这些问题可引入工程界最常用的振动模态来解决，即频率和振型[5]。相对测量精度来讲，结构固有频率不仅测量方法简单，而且测量精度比振型精度高[6]。所以，如能用结构频率的改变量识别梁结构的损伤具有很大的工程应用前景。薛松涛等[7]对此方面的研究主要集中在频率灵敏度方法上，但频率灵敏度存在数据量过少以及不适于对称结构的缺点；陈小超等[8]应用移动质量法与分形维数实现梁损伤检测;Zhong S[9]、李雪松等[10]基于附加质量的方法提出新的损伤指标能解决数据量过少的缺点。这些研究在检测中都使用了大量的检测仪器来测量桥梁多点的模态参数，但由于现阶段传感器的局限，很难测量到准确的桥梁振型。据此，该文将模态参数进行组合提出新的损伤指标。该指标具有以下优点：附加质量后结构转化成非对称结构，不同位置的损伤引起不同的模态参数的改变，解决了对称结构对损伤识别的影响；新的损伤指标中利用频率的改变量，而且将附加质量在不同位置附加可得更多的频率参数，所以精度有一定的保证。该指标仅需梁结构上单点模态振型参数即可判断损伤位置，对于梁结构工程损伤检测具有一定的工程应用价值。

1 单点模态振型参数损伤指标的提出

将不同位置附加的质量简化成一个常量力[11]作用在同截面梁结构的对应位置。下面以一个简支梁结构在一个常量力作用于不同位置下的动力响应为切入点[12]，对结构进行动力分析后提出新的损伤指标。

图1中将同截面梁结构分为等间距的M个子结构，每个子结构的长度为l0=l/M，将附加质量简化为常量力作用在同截面简支梁各子结构间的节点位置。假定在开始时，常量力作用于左端固定铰支座处，在变量为i时，常量力F=mg向右移动到距离左端支座为li=i×l0(i=1,2,3,…,M)的位置。忽略梁结构的阻尼，该同截面梁结构在荷载作用下的振动方程为：

(1)

式中：m(x)为梁的总质量；E为梁的弹性模量；I为梁的惯性矩；f(x，t)为作用在梁上的作用力。

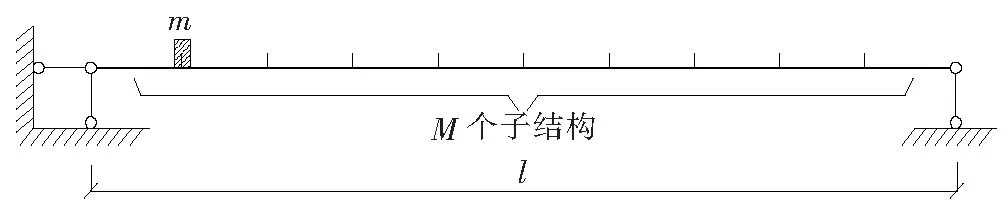
图1 梁结构图

由模态分析理论对方程的解可表示成所有阶模态振型的和：

(2)

式中：y(x，t)为梁的响应值；φj(x)为位移模态振型；qj(t)为模态坐标；j为振型阶数。

将式(2)代入式(1)中：

(3)

对式(3)两边同乘以φn(x)dx，然后对x积分得：

(4)

根据振型正交性：

(5)

(6)

式中：ωk、mk分别为第k阶频率、模态质量。

根据式(5)、(6)对式(4)简化得：

(7)

式中：Fn(t)为外部荷载力f(x,t)基于模态坐标qn(t)的广义荷载力。

因为附加荷载为常量力，所以f(x,t)可以用式(8)代替：

f(x,t)=F×δ(x-li)

(8)

同截面简支梁的振型模态可以表示为：

(9)

将式(8)、(9)代入式(7)中，假定梁结构的总质量m(x)为m不变，得到：

(10)

根据初始条件，求解式(10)的解：

(11)

于是可得同截面梁结构在常量力作用下动力响应方程为：

(12)

将式(9)代入式(12)中，得：

(13)

简写为：

(14)

对式(14)求x的二阶导数：

(15)

由式(15)分析ψn的表达式中，有ωn含有变量x，φn是结构模态振型，为全面准确地反映出结构由于损伤造成的动力响应表达式的改变，提取结构附加质量后动力响应的频率与模态振型的二阶导数组合成目标函数来识别损伤。

附加质量在子结构的不同节点处可以获得节点处的n阶频率，将所获得各频率按照如下位置构成矩阵：

(16)

式中：ωn,i为在第i节点处获得的第n阶频率。

与频率值相对应的振型模态：

(17)

根据式(15)提出近似简化损伤识别指标：

(18)

式中：Δω″n,i为频率损伤前后的二阶导数差；Δφ″n,i为对应振型损伤前后的二阶倒数差。

实际工程中，测量的模态振型参数点与所得数据成正比，对损伤识别指标的精确度影响越大，但是，成本以及运营条件却不允许越大。在分析中发现利用附加质量识别时，梁上任一点的振型参数都可以近似反映该梁振动响应。所以提出单点振型参数的损伤识别指标：

(19)

式中：Δω″n为频率损伤前后的二阶导数差；Δφ″n为任一点对应振型损伤前后的二阶导数差。

然后，将所获得的频率矩阵式(16)、模态振型矩阵式(17)二阶导数的乘积与原系统联立起来求解各损伤参数。

[α][φ″nω″n]=[φ″nsω″ns]

(20)

式中：[α]=[1-α1,1-α2,…,1-αN]T；φ″nsω″ns为原系统振型模态与频率的二阶导数乘积。

2 数值模拟分析

2.1 有限元模型

通过有限元分析软件建立同截面简支梁模型如图2所示，在模拟的过程中，损伤用刚度的折减实现，在软件中用弹性模量的折减实现。图2中梁总长1 m，宽0.05 m，高0.005 m。弹性模量E=2.1×1011MPa，泊松比0.3，密度ρ=7 850 kg/m3。模拟时将梁结构分成20个单元，每单元长度0.05 m。假设13号单元发生损伤，刚度(弹性模量)在无损状态下减小40%，即损伤参数取0.4。

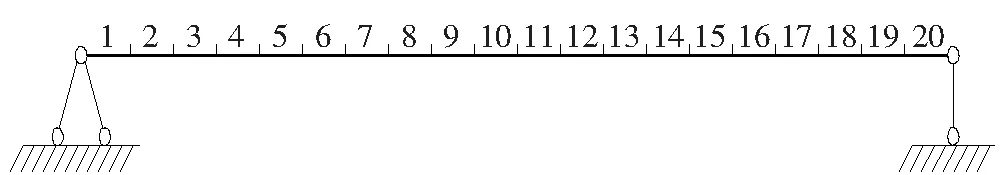
图2 简支梁图

2.2 损伤识别分析

沿同截面梁结构的长度方向在每个单元节点上依次附加0.1 kg质量，即可得到随附加质量位置变化的1阶固有频率值，同时可得到结构任一节点振型的变化值。图3为假定13号节点损伤40%时，在2号节点采样得到的附加质量在各个节点处结构频率变化以及振型变化。

从图3中得到将附加质量沿梁结构的长度方向移动时，相应的频率值以及模型节点的振型都会出现先减小再增大的规律变化。然后根据该文提出的单点振型参数损伤识别指标(βASS)对该简支模型梁2号节点分析的结果如图4所示，由于1、21号节点为支座节点，附加质量对其影响几乎为零，该文中不再考虑。

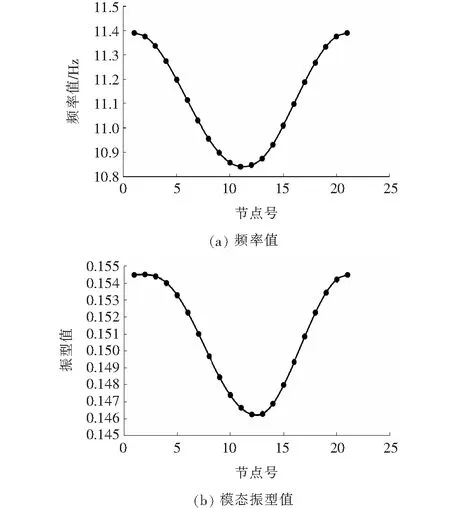
图3 附加质量位置变化作用结果

图4 损伤识别指标(βASS)

根据图4可以得到:在节点13、14处βASS值出现明显突变，可定义为两节点间的单元出现损伤。验证了上文中所提指标βASS能够在梁结构损伤时准确识别出模型梁13号单元为损伤位置，与预先设定相同。

对于损伤程度，根据所得单点数据亦可进行判定，由上文式(20)中1阶频率二阶导数与振型点位二阶导数的乘积在损伤前后的比值分析，即可得出损伤单元的损伤程度。由上述模型2号节点所得数据对13号单元(两节点均值)进行损伤参数求解所得：

α13=1-0.600 316=0.399 684。

所求解值与预先设定损伤参数0.4对比识别的损伤程度误差率仅为0.08%，基本接近零的误差。所以上文提出的新指标βASS能够在梁结构损伤时准确识别位置与损伤程度。

2.3 不同损伤程度的识别分析

将损伤程度设定为不同的等级以分析验证该损伤参数识别的正确性。把上文中模型的13号单元的损伤参数设定为0.1、0.2、0.3、0.4、0.5不同的5个工况，从而验证损伤指标的识别精度。依次在各节点附加0.1 kg质量，得出模态振型参数，运算得出单点振型参数的损伤识别指标βASS来识别损伤位置，图5为2号节点各工况下损伤识别的结果。

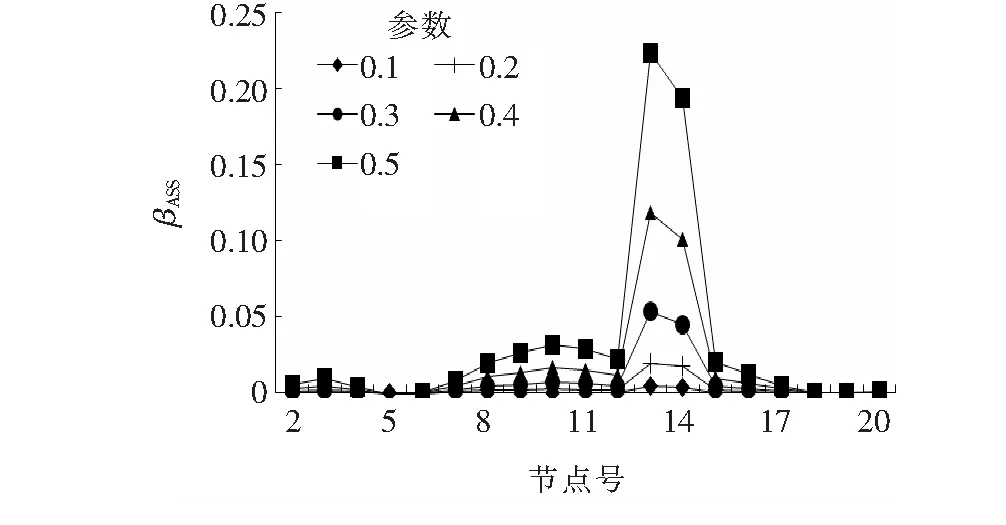
图5 各工况下损伤识别结果

由图5可以看出：βASS可准确识别损伤位置，且随损伤参数的增大损伤指标的敏感性越大，识别的效果越好。对损伤程度进行识别结果如表1所示。

由表1可以看出：所提出的单点振型参数的损伤识别指标βASS基本能够准确识别各种损伤程度，对于小程度损伤参数为0.1时识别的误差较大，但是也能保证在10%以下，随损伤参数的增大识别误差呈现先减小后增大的趋势。所以判断该指标能够在不同损伤参数下准确地识别损伤位置以及损伤参数。

表1 损伤参数识别结果

2.4 附加质量对βASS指标影响分析

为研究附加质量对βASS指标的影响，对附加质量大小进行改变，控制其余参数不变，定义13号单元损伤参数均为0.4。分析中设置如表2中的5个工况对梁结构进行单点振型参数的损伤识别指标βASS模拟分析。最终得出各工况下βASS指标值如图6所示。

表2 附加质量工况

图6 各工况下βASS指标值

从图6各工况下βASS指标值可以看出：在各附加质量工况下利用新提出的损伤指标都可以准确识别损伤位置。而且，随着附加质量的增大指标值也在增大，也就是说附加质量越大指标越敏感。然后根据模型在各工况下2号节点所得数据对13号单元进行损伤参数识别，结果如表3所示。

表3 附加质量损伤参数识别

根据表3中结果所得，所有工况识别出损伤参数误差均在3%以下，而且工况2、3的识别误差最小，可以初步认为所提出指标附加质量占梁总质量的5%～7.5%时识别精度较高。

2.5 分析点的影响

上文中仅对2号节点所得数据进行分析，对于该模型梁共有19个节点(支座节点不考虑)都可进行损伤识别，该小节对该模型梁节点与所提出损伤识别指标之间关系进行研究。利用上文中损伤位置确定与损伤参数识别的方法，对13号单元损伤参数为0.4时进行识别。首先对2～20号节点所得数据进行损伤位置判断，结果如图7所示。

图7 各节点所得数据损伤识别结果

由图7所得：所有节点的数据都可根据指标βASS判断出损伤位置。然后对该模型13号单元的损伤参数进行识别，为简便表述使用13号节点的数据作为识别结果。如表4所示。

根据表4分析各节点损伤参数识别结果，在靠近固定铰支座一端识别损伤参数的误差很小，接近零。而在滑动铰支座一侧识别损伤参数的误差较大。

表4 分析节点损伤参数识别

3 结语

基于附加质量提出了单点模态振型参数损伤指标βASS用以识别同截面梁结构损伤的方法，通过数值模拟算例验证了该损伤识别指标能够准确识别结构损伤位置以及在不同损伤参数下的有效性。对附加质量大小与分析点关于βASS指标影响进行分析，得出所提出指标在附加质量占梁总质量的5%左右以及靠近固定铰支座一端识别精度较高的结论。

该指标是将模态参数进行组合提出新的损伤指标识别方法，附加质量使对称结构转化成非对称结构，不同位置的损伤引起不同的模态参数的改变，有效解决了对称结构对损伤识别的影响。新的损伤指标中也用到结构频率的改变量，识别精度有一定的保证。而且，在所提出识别方法中只需同截面梁结构上单点的模态振型参数即可对损伤位置判断。对于梁结构工程损伤检测有一定的工程应用价值。