基于PFC模拟的曲线漏斗筒仓动态压力研究

赵光明 程远浩

1.华电重工股份有限公司 北京100070

2.机械工业第六设计研究院有限公司 郑州450007

引言

筒仓在卸料过程中动态压力会骤然变大已成为共识，但动态压力增大的原因在国内外尚未有统一的理论基础［1-4］。因此正确认识筒仓动态侧压力的增大机理，进而通过有效手段避免筒仓安全事故的发生是目前所急需的。

有学者提出在筒仓内部安装减压装置，以达到降低筒仓动态侧压力的目的。董承英［5］、徐志军等［6］提出在筒仓侧壁卸料时，在卸料口上方安装流槽，通过改变流态来降低筒仓动态侧压力，但偏心卸料方式在新型筒仓中并不常用，不适用于大部分筒仓。Shie-Yang 等［7］、戴则祐［8］、余平等［9］针对中心卸料，通过在卸料口处安装减压管来改变筒仓的流态进而降低筒仓动态压力，但在实际筒仓卸料过程中存在减压管不易于安装固定且影响筒仓装料等问题。

1963年，有学者提出双曲线漏斗的思路［10，11］，将截面收缩率不断增大的锥形漏斗，改为截面收缩率恒定的曲线漏斗。在实际工程中，曲线漏斗在提高流速、降低筒仓侧壁压力等方面都取得了良好的实用效果。Wang 等人［12］通过试验证明了曲线漏斗具有更好的流动性。李海旺等［13］利用PFC模拟对裤型漏斗进行卸料模拟，验证曲面墙壁受到的动态压力小于直面墙壁。李宝明［14］以圆弧包板式煤炭漏斗车为研究对象，给出了散体煤对漏斗车车体的静、动态侧压力的大小及分布规律。宋加宏等［15］通过几何理论对双曲线煤仓容积进行计算分析。Hanru［16］利用DEM 对不同收缩率曲线漏斗筒仓贮料的出料速率进行对比，发现收缩速率存在临界点，当收缩率等于临界点时，颗粒的流动速率最大。

本文利用PFC模拟的方法，分别对直线漏斗筒仓和曲线漏斗筒仓进行卸料研究，分析两种筒仓在卸料过程中动态侧压力的变化，为曲线漏斗的设计提供参考。

1 曲线漏斗筒仓相关计算

1.1 曲线漏斗工作原理分析

直线漏斗的截面积收缩率随其高度的下降而增大，每下降一个微小高度，颗粒都要重新排列以适应漏斗截面渐渐减小的变化，越接近出料口，截面积越小，截面收缩越快，内摩擦阻力越大。当摩擦阻力的合力超过颗粒自重产生的垂直静压力时，仓内贮料停止流动，从而导致漏斗部分以及漏斗上部贮料堵塞起拱。

尤其在储煤仓中，仓内存煤的水分高、粉煤多、易泥化、粘结力强等内在原因，更是加剧了这种现象的发生概率。曲线漏斗截面收缩率是一个定值，而斗壁上任何一处的倾斜角是变值，越接近斗口时斗壁倾斜角越大，物料在下流时横向挤压无明显增加，可防止堵塞。

1.2 曲线漏斗相关计算

图1 为曲线漏斗各参数计算示意，首先根据《建筑结构设计手册-贮仓结构》，确定曲线漏斗单侧壁曲线计算公式、筒仓漏斗高度计算公式、截面收缩率计算公式、曲线漏斗侧壁任意位置切线角计算公式分别为：

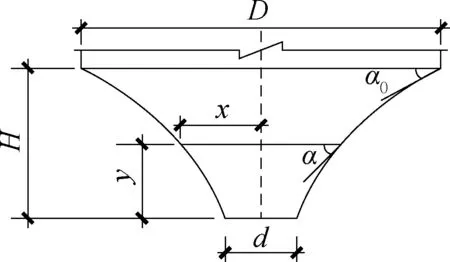
图1 曲线漏斗计算示意Fig.1 Schematic diagram of curve funnel calculation

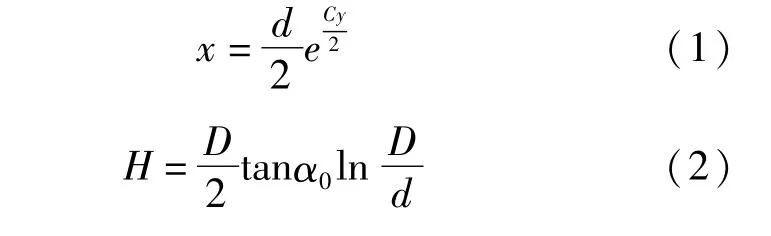
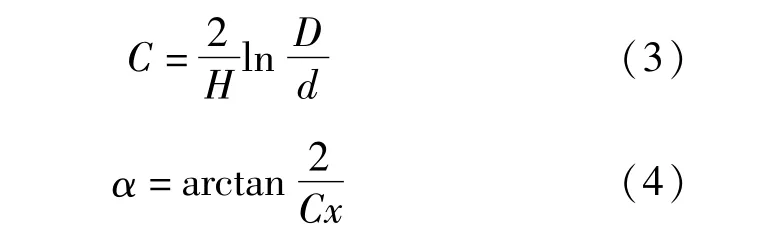
式中：D为漏斗上顶直径（m）；d 为卸料口直径（m）；H 为高度（m）；α 为仓壁切线角（°）；α0为曲线漏斗初始角（°）；C为截面收缩率。

2 两种筒仓PFC模拟动态侧压力结果对比分析

2.1 模型建立

离散元法是一种采用非连续介质模型的数值模拟方法，较之于有限元的连续介质模型，离散元法更贴合筒仓卸料的实情。模型仓以广西某储煤筒仓为依据，原仓高50m，直径27m，高径比为1.85，模型仓等比缩小50 倍，漏斗分别选用倾角为30°的锥形漏斗和初始角为30°的曲线漏斗，将α0＝30°、D ＝0.54m、d ＝0.08m，相继代入式（2）、式（3）中，求得曲线漏斗高度与截面收缩率。将沿漏斗高度方向三等分节点高度值带入式（1）得到与之对应的x 值。最后将截面收缩率与节点的x 值代入式（4）中，可得各节点处的切线角，见表1。

表1 各节点处的切线角Tab.1 Tangent angle at each node

在PFC2D中通过wall命令，建立了筒仓模型，图2 为两种筒仓卸料过程。建立20 段测墙，沿仓壁两列布置，间隔0.1m。颗粒通过ball 命令生成。颗粒粒径为0.001m ～0.01m，重力密度为7.5kN／m3，与煤的物理参数保持一致。颗粒的法向、切向刚度，墙的法向、切向刚度等物理参数通过试验结果对模型进行反复标定来确定，例如，首先通过理论计算公式［17］得出颗粒的法向、切向刚度参考值，然后采用控制变量的方法，不断调整参考值，使得测得的静态压力值接近规范值，最终得到颗粒的法向、切向刚度准确值，具体模拟参数见表2。

表2 模型的主要物理力学参数Tab.2 Main physical and mechanical parameters of the model

图2 模拟仓示意Fig.2 Schematic diagram of simulated bin

2.2 静态侧压力分析

在14 层颗粒全部生成完成之后，执行数次消能循环命令，直至达到静态平衡状态。分别记录下两种筒仓每个测点静态压力值（静态压力值为两列静态压力的平均值），图3 为两种筒仓各个测点的静态压力值与理论计算值随深度变化的折线图。可以看出在PFC2D模拟得到的静态压力值在大小和趋势上与理论值相差不大，存在一些差异，但在可接受范围之内。说明试验和模拟的结果均较为可靠。

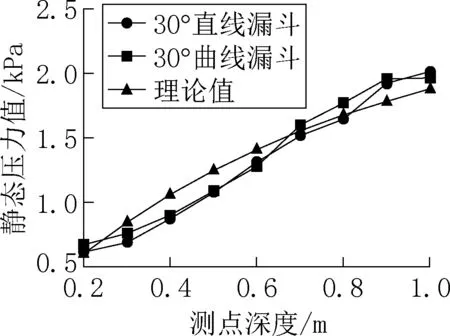
图3 两种筒仓静态压力值与理论值Fig.3 Two silo static pressure values and theoretical values

2.3 动态侧压力分析

在记录静态压力值后，执行卸料命令，提取两种筒仓各测点的最大动态压力值（两列取平均值），见表3。并绘制出动态侧压力与测点深度变化关系的折线图，见图4，以便更清晰地观察直线漏斗与曲线漏斗的不同。

表3 两种筒仓动态侧压力值汇总Tab.3 Summary of dynamic side pressure values of two silos

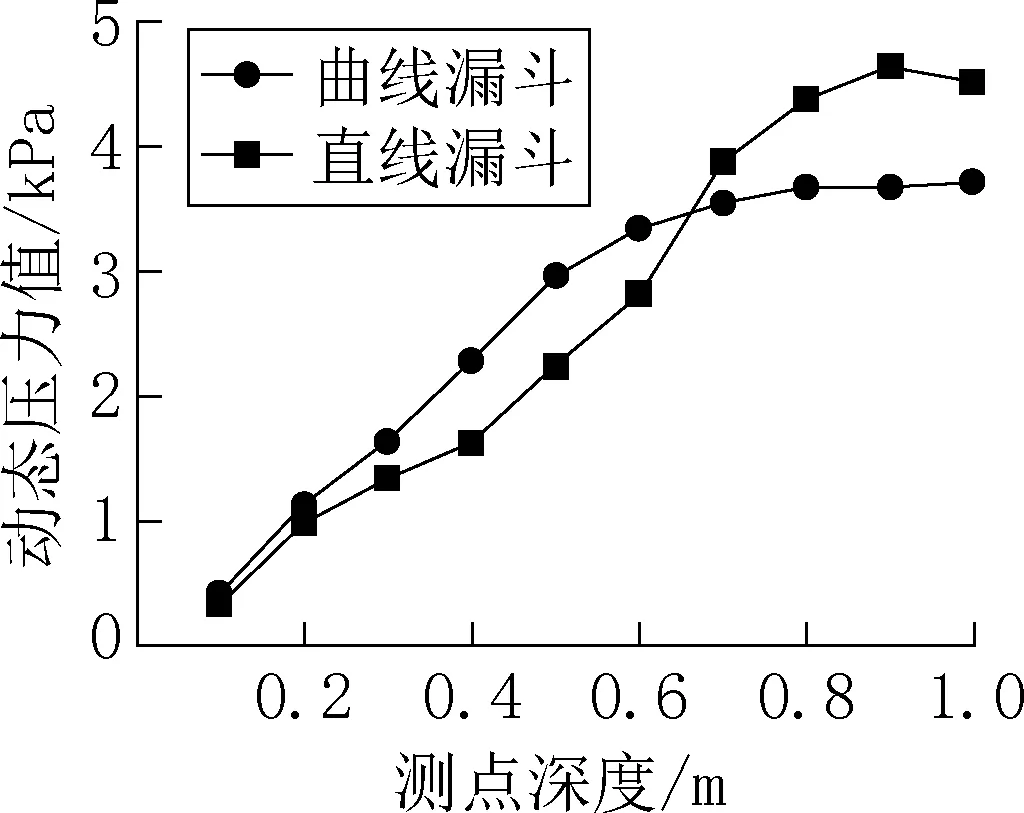
图4 各测点的最大动态压力值对比Fig.4 Comparison of the maximum dynamic pressure value of each measuring point

可以发现，直线漏斗筒仓和曲线漏斗筒仓动态侧压力值的大小与分布存在明显的不同，直线漏斗筒仓最大动态侧压力出现在0.9m深度处，最大动态侧压力值为4.631kPa，曲线漏斗筒仓最大动态侧压力出现在1.0m 深度处，最大动态侧压力值为3.715kPa。在0.7m ～1.0m 范围内，直线漏斗筒仓中较大动态侧压力值大于曲线漏斗筒仓。其中在0.9m深度处，两者差值尤为明显，达到0.955kPa。

通过对比可以发现，两种筒仓动态侧压力均随着仓壁深度的增加而增大，在筒仓底部达到最大，筒仓底部也是最容易发生超压破坏的位置，而曲线漏斗可以降低筒仓底部仓壁处的动态压力值，对筒仓提供有效的保护。

3 结论

本文采用离散元数值模拟的方法，研究直线漏斗筒仓和曲线漏斗筒仓在卸料过程中动态侧压力和流态的变化。分析曲线漏斗改善流态的原因，得到以下结论：

1.两种筒仓静态压力相差不大，说明筒仓静态压力在筒仓形状不变的情况下只与筒仓装料高度有关，与漏斗形状无关。

2.在筒仓壁外形尺寸一致的情况下，卸料过程中直线漏斗筒仓较曲线漏斗筒仓仓壁最大动态压力值高出24.66%，说明曲线漏斗可以降低筒仓动态侧压力，对筒仓有一定的保护作用。