真空系统抽气性能的数值仿真分析

郭嘉炜,黄 思,李松峰,吴泰忠

(1.华南理工大学 机械与汽车工程学院， 广州 510641；2.广东肯富来泵业股份有限公司， 广东 佛山 528131；3.广东省节能环保装备用泵企业重点实验室， 广东 佛山 528131)

0 引言

真空系统主要由真空泵、真空室(被抽容器)、管道、阀门和控制仪表等元件组成，广泛应用于工业生产和各个技术领域[1-3]。真空泵的抽气速率Sp与吸入压力Po的特性关系是决定真空系统性能的主要因素，真空泵机组启动时，被抽容器内部气体经由连接管路排出，泵吸入压力与容器压力逐渐降低。因此，如何快速准确地根据真空泵特性对真空系统抽气过程和结果进行预测，对真空系统设计选型以及运行调度具有重要意义。

近年来，国内外学者相继开展了真空系统抽气性能的研究。在理论计算方面，孔祥龙等[4]和许海虹[5]对真空系统设计方案给出了抽气时间公式，采用抽气过程中抽速恒定的假设，与真空泵实际工况有所区别，计算结果与实际情况会有一定的偏差；为此，部分学者考虑了真空泵抽气速率实际变化的情况，隋吉秋[6]计算了某容积为740 m3的空间环境模拟器的理论压降曲线，与实测对比误差较大；焦喆[7]考虑了抽速变化，建立了容器抽空过程计算的数学模型，并编程对抽气过程进行离散化计算；黄思等[8]以中低真空系统为研究对象，根据管路流动状态选取层流或湍流模型，提出一种新的抽真空时间计算方法，得到了实测结果的验证。在数值模拟计算方面，刘金策[9]以及隋吉秋[6]分别以FLUENT和CFX验证了目前商用计算流体动力学(computational fluid dynamics，CFD)软件真空模拟中低真空(即湍流和粘滞流)是可行的；隋吉秋[6]利用CFX实现了恒定抽速的抽真空过程，但与实际变抽速的过程不符；潘欣钰[10]利用CFD方法模拟大空间抽真空项目的充气过程，证明CFD在模拟大空间负压的变化过程是可行的。综上所述，无论是理论建模还是三维CFD模拟计算，都不太适合多元件且结构复杂的真空系统分析。

Flowmaster是研究流动系统尺度的一维仿真软件。该软件将流动系统中的各个元件使用节点连接，使流体在各元件满足连续性方程、动量方程和能量方程等流动控制方程，它既能计算元件处的流动特性，也可以计算节点处的流动特性。相对于三维数值模拟，Flowmaster具有建模方便、计算速度快等特点，适用于流动系统整体性能的分析计算。因此，本文选取某真空泵组系统作为研究对象，应用Flowmaster研究特定工况下的系统抽气性能，为真空系统设计选型及合理运行提供技术支持。

1 计算模型及方法

1.1 真空系统问题概述

图1为本文选取的研究对象示意图。真空室容积V0=129 600 m3，主管道总长Lm=10 m，直径Dm=2 m，在8、9、10 m处分别有长度Lf=10 m，直径Df=1 m的支管，末端连接同型号的真空泵，管道的相对粗糙度均为0.01。单台真空泵的抽气速率Sp与吸入压力Po的关系曲线如图2所示，拟合后的关系式见式(1)。真空室内介质为20 ℃空气，黏度μ=1.820×10-5Pa·s，密度ρa=1.205 kg/m3，泄漏量Sm=2 kg/s，初始压力为P0=96 kPa，终止压力为Pe=10 kPa。该系统抽气时间t与真空室压力P的设计指标应达到：①P-50 kPa，t≤15 min；②P-20 kPa，t≤30 min；③P-10 kPa，t≤50 min。

图1 真空系统示意图

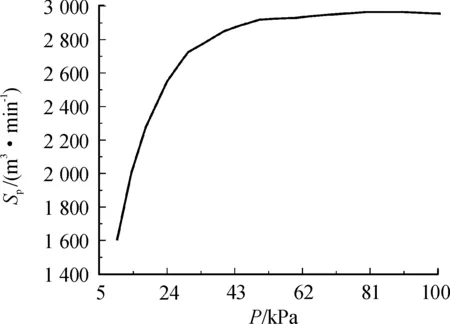
图2 单台真空泵Sp-Po特性曲线

(1)

1.2 Flowmaster计算方法验证

数值计算方法模拟仿真具有使用方便，成本较低的特点，三维CFD软件是在单个元器件的尺度上进行三维流场仿真，而一维数值模拟计算的是系统尺度上的变化，如各支路流量的变化及各节点压力的变化。三维的CFD软件进行计算，对于不需要流场可视化的案例进行计算时，存在建模复杂、需要划分网格且计算耗时较长的缺点，而一维数值模拟相对于三维数值模拟具有建模方便、计算速度快等优点，适用于考虑系统整体性能的分析计算。Flowmaster是一维流体系统仿真解算工具，已内置了丰富的元件库，对于各种流体系统，可以快速有效地建立精确的系统模型。

Flowmaster基于特征线法，将系统分解成一系列的流动元件，元件之间根据节点进行连接，且各个元件满足动量方程以及连续性方程等条件，既能计算元件处的流动特性，也可以计算节点处的流动特性。Flowmaster求解流动方程前，先对流动方程做线性化处理得到线性方程组，再求解压力、流量等参数。以如图3的两接口元件为例，方程组包含进出口质量流量随压力变化的方程：

图3 两接口元件示意图

(2)

其中：A1-A4用于描述压力变化对质量流量的影响，B1与B2用于描述非压力变化的部分。对于不同的元件，其特性对应不同的流量-压力关系，经推导并导入上述的方程组后，不同的元件根据节点关系建立整个系统的系数矩阵，即可求解系统的流动参数。

本文采取与理论方法[8]和Fluent三维模拟计算结果对比的方式验证Flowmaster对真空系统计算的有效性。

将图1的研究对象简化为如图4所示中低真空系统，该系统可简化为由真空室、抽气主管道和真空泵机组所组成。假设流体介质为理想气体，抽气过程近似为等温过程。3个泵在主管道末端并联，等效为一个泵。

图4 理论计算简化真空系统模型

真空系统的抽气方程满足[8]：

(3)

式中：C为总管道流导，m3/s。假定管道粗糙度为0.01，湍流时，相对粗糙度为0.01时，可取阻力系数λ=0.04，按照文献[8]的方法推导管道流导C[8,12]：

(4)

按照文献[8]方法对式(3)进行离散化计算，设定压力变化步长为1 Pa，计算真空室压力P与对应抽气时间t。

根据图1所示的系统及图2所示的真空泵性能曲线在Flowmaster内建立如图5所示的简化计算模型。系统中由真空室、主管道以及3台真空泵合并的机组构成。元件1为真空室，选用accumulator:gas，介质为气体(Gas)，对该元件输入体积和初始压力，近似认为抽气为等温过程，多变指数n=1，抽气过程视作等温过程；元件3为真空泵机组，选取Source:Pressure vs.Flow方式，该部件可采用自定义的泵特性曲线进行计算，对该元件输入3台真空泵合并的特性曲线；元件4为真空系统的泄漏量，选用Source:Flow方式，可设定固定的泄露质量流量，对该元件输入已知的泄漏流量；元件2为主管道，设置管道长度、直径及相对粗等参数；元件5为Y型管，用于真空室与泵抽气和泄漏点的连接。设置计算时间步长为Δt=0.1 s。

图5 Flowmaster真空系统的简化计算模型

Fluent流体域模型以及计算网格如图6所示，真空室长、宽、高分别为51.84、50、50 m，管道位于真空室侧面中心处，划分后的计算网格数为48 120。重力加速度为9.81 s/m2，假设空气为理想气体，湍流计算选择k-ε湍流模型，重力加速度为9.81 m/s2；壁面温度、真空室内初始温度及泄漏环境温度为293 K，壁面与外界绝热，真空室壁面泄为2 kg/s；按Sp-Po关系式(1)采用用户自定义函数(user defined functions，UDF)编程设置出口边界条件以实现真空泵抽速随真空室压力变化而改变的特性，采用速度出口，计算时间步长为Δt=0.1 s。

图6 Fluent流体计算域及网格划分图

图7给出了按理论方法[8]、Fluent和Flowmaster分别计算得到的真空室平均压力P随抽气时间t变化的对比情况。其中Fluent采用体平均方法统计真空室温度，虽然壁面为隔热设置，但由于设置理想气体选项计算抽气过程温度变化，影响压力计算结果，应进行修正处理换算为293 K下的压力[11]。由图7可见，3种算法计算结果趋势一致且数值上有较小偏差。

图7 真空室平均压力P随抽气时间t的变化曲线

表1给出了上述3种计算方法到达50、20、10 kPa所需的抽气时间t。由表1可见，Flowmaster与理论计算结果比较接近，Flowmaster计算与Fluent计算达到50、20、10 kPa的时间相对分别为3.42%、3.66%和3.60%，偏差较为稳定。根据Flowmaster与其余2种算法的计算结果对比，可知Flowmatser用于真空系统抽气性能计算是切实可行的。

表1 不同计算方法达到压力指标的时间

2 Flowmaster计算应用

2.1 Flowmaster实际计算模型

如图8所示，在工程应用中可根据流动系统的具体情况建立更为符合实际的计算模型。将图2的真空泵Sp-Po特性曲线添加到元件3、10和12的真空泵元件中。采用Junction:T (90°)方式，增加元件6、7、16的T型管；采用Source:Blank End (Zero Flow)方式，元件13以中止流体在主管道末端的流动，其余元件的类型和计算设置与相同。

图8 Flowmaster真空系统的实际计算模型

2.2 Flowmaster计算结果分析

图9是Flowmatser实际计算模型若干元件压降ΔP随时间t的变化曲线，图10给出了图5(泵机组合并)和图8(泵机组未合并)2个不同Flowmaster的真空室压力P随抽气时间t的变化。由图9可见，3条曲线均呈随时间快速下降的趋势，其中管道2，9分别是主管道末段和首段，管道9只有一个泵作用，压降极小，阻力可忽略不计，在管道2由于3个泵同时作用流速增大且管道长度增加的原因，压降较大；管道15为代表末端真空泵支管道的压降，管道15的压降大于主管道，相对于直径不变的主管道和支管道，连接主管道和支管道的T型管对压降的影响更大，到抽气过程后期，即使主管道压降接近0 Pa时，T型管压降仍较大。由图10可见，两者趋势相同，结果接近，同一时间t的压力偏差值ΔP随着抽气过程存在先变大后减小的趋势。表2给出了2个模型达到50、20、10 kPa共3个压力指标的所需抽气时间t。由于管道的阻力，图8的实际计算模型达到3个压力指标的所需时间t均增多。模型1、2达到50、20、10 kPa的时间绝对值偏差分别为19、49、74 s，相对值偏差分别为3.25%、3.19%和2.90%，偏差逐渐减小。因此，相对于管径不变的主管道和支管道，T型管阻力是影响抽气过程的最主要因素，不可忽略，T型管阻力对达到特定压力指标所需时间的影响随着抽气过程进行而减小。

图9 Flowmatser实际计算模型若干元件压降ΔP随时间t的变化

图10 Flowmatser模型1、2压力P随抽气时间t的变化曲线

表2 Flowmatser模型1、2达到压力指标的时间

图11、12分别是按图7所示的实际计算模型计算得到的若干节点压力P与密度ρ随时间t的变化曲线，图11中第1条曲线是节点11处真空泵入口压力，此时未受管道影响；第2条曲线是节点14处，位于支管道进口端，压力受支管道阻力的影响；第3条曲线是节点8处，位于T型管进口端，压力受T型管分支处直径变小的影响。由图11可见，在抽气的早期阶段，曲线1、2的差值相对于曲线2、3的差值较小，说明T型管由于进出口直径大小变化对于管道阻力的影响更大；随着时间增加，3条曲线接近重合，T型管还有管道阻力的对压降影响已不明显，在真空室压力达到 10 000 Pa，上述3个节点的压力分别为9 916、9 942、9 995 Pa，相对偏差不足1%。图12中，密度ρ的变化趋势与压力P一致，符合理想气体的中压力与密度为线性关系的规律[12]，其中T型管曲线与其余偏差比较明显，说明相比管道沿程阻力，T型管的局部阻力对气体密度变化影响更大。

图11 Flowmatser实际计算模型若干节点压力P随时间t的变化曲线

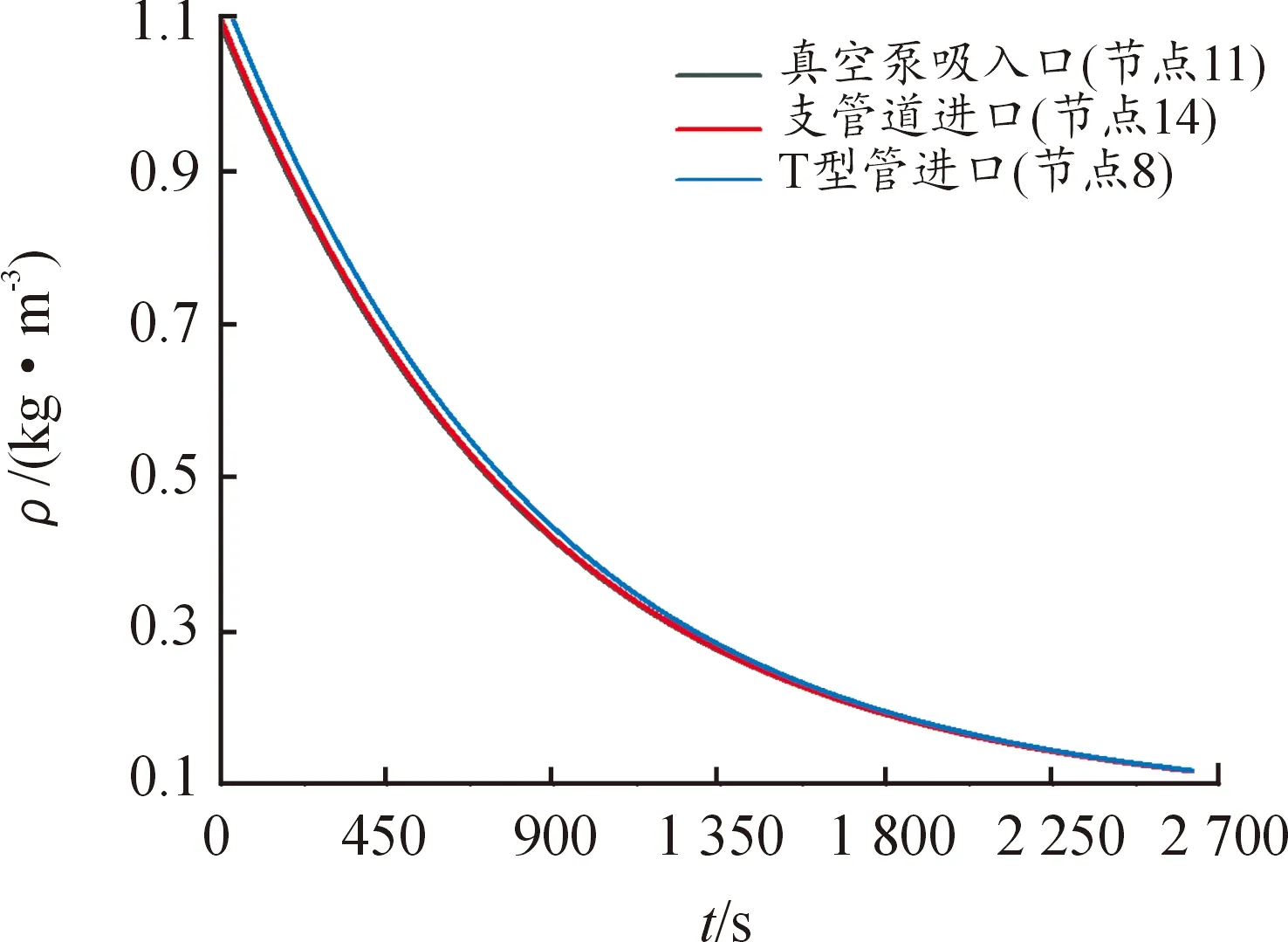
图12 Flowmatser实际计算模型若干节点密度ρ随时间t的变化曲线

图13、14分别给出了实际计算模型中若干节点的气体流速v与对应元件雷诺数Re随时间t的变化曲线。按照图8的建模，节点12、13、14分别是管道14、11、15的进口处，代表了3条支管道的气体流速；管道2连接有3台真空泵，节点2位于管道2的进口处，因此节点2流速代表了主管道初始端的气体流速；管道9连接有一台真空泵，节点7位于管道9的进口处，节点7流速代表了主管道末端的气体流速。由图13可见，节点2速度为节点7的3倍左右，与3个真空泵同时作用的工况相符合；节点12、13、14的3条支管道进口处气体流速曲线重合，说明在管道阻力很小的情况下支管道流速v没有因为管道排布位置不同而产生差别。相对于流速v变化，雷诺数Re随时间t变化更加明显，这是因为雷诺数Re∝ρv[13]，除了受气体流速v的影响，还受气体密度ρ的影响。对于整个抽气过程，整个系统中管道2的雷诺数最大，而管道9的雷诺数最小，但即使雷诺数最小的管道9，计算终止时其雷诺数Re仍远大于2 000，这意味着本文研究的真空系统的所有管道在整个抽气过程中基本处于湍流状态，由此可见文献[8]提出的考虑湍流的理论方法是合理的。

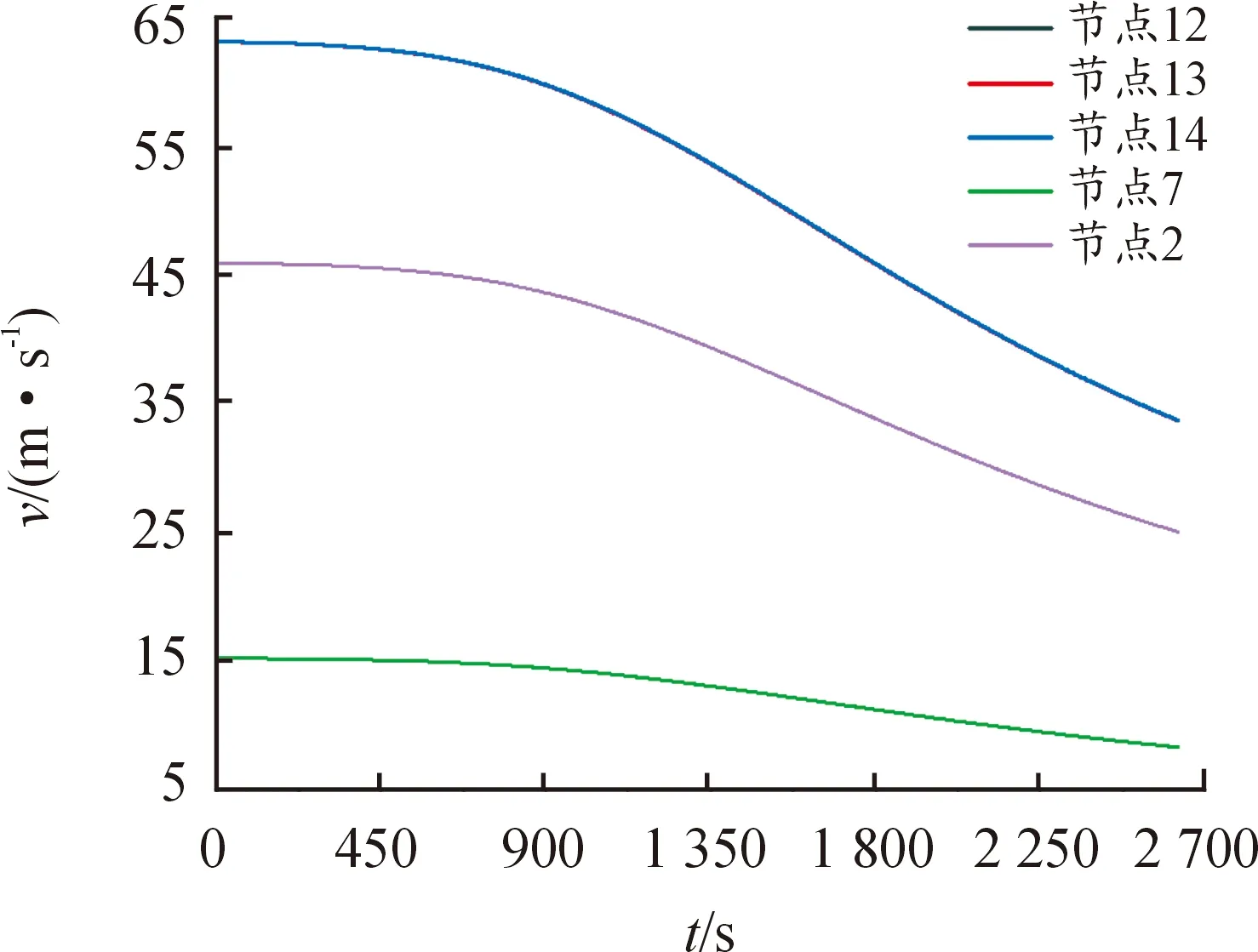
图13 Flowmatser实际计算模型若干节点流速v随时间t的变化曲线

图14 Flowmatser实际计算模型管道雷诺数Re随时间t的变化曲线

3 结论

1) 所研究的真空系统管道在整个工作过程中基本处于湍流状态，因此理论计算模型需要考虑湍流因素并采用合适的方法进行计算。

2) 在所研究的真空系统中，与管道沿程阻力相比，T型管所产生的局部阻力对压降和密度等气体参数变化影响更大，T型管阻力对达到特定压力指标所需时间的影响随着抽气过程进行而减小。

3) 对于简化的真空系统，采用Flowmaster与三维CFD软件计算的系统性能参数变化趋势一致、偏差较小，表明应用流动系统尺度的一维软件，可以有效地分析多元件且结构复杂的真空系统。