分布式驱动差动转向汽车的纵横向力协调控制研究
2022-11-07张纯涛
田 杰,张纯涛
(南京林业大学 汽车与交通工程学院, 南京 210037)
0 引言
分布式驱动电动汽车采用轮毂电机驱动,在节能减排方面展现出巨大的优势[1-2]。轮毂电机运行噪音低、峰值效率高、负荷能力强[3-4],同时由于其转矩独立可控,且转矩响应快速精准[5-6],能有效改善车辆的操纵稳定性和安全性[7],因此成为研究热点。此外,分布式驱动电动汽车还可通过独立控制左右前轮的驱动力矩差来实现汽车的差动转向[8]。它既可以用作线控转向的后备系统,又可以用作汽车唯一的转向系统,后者可进一步简化汽车的结构。

综上所述,目前对差动转向汽车的研究往往只关注单一的横向或纵向的运动。其实,由于轮胎附着椭圆的限制使汽车的纵横向运动之间有一定的耦合关系,也就是说,在特定附着系数路面上,纵向力过大往往会使车轮可以提供的最大横向力减小,反之亦然。此外,汽车转向时,车身的侧倾会加剧车辆的侧向运动,并影响到汽车的纵向行驶车速[17]。因此,针对分布式驱动差动转向电动汽车提出了轮胎纵横向力协调控制的方法,旨在保证转向时汽车纵向速度恒定的同时,每个车轮均不出现滑移,从而提高汽车的操纵稳定性。
1 动力学模型的建立
1.1 分布式驱动电动汽车的动力学模型
本文研究的分布式驱动电动汽车采用四轮轮毂电机驱动。为简化车辆动力学模型,忽略汽车的俯仰和侧倾,采用如图1所示的分布式驱动电动汽车的动力学模型。其中,ls为左右前轮距离的一半;lf、lr分别为车辆质心距前后轴的距离;β为车辆质心侧偏角;vx、vy分别为整车的纵向速度和侧向速度。Fxi表示轮胎的纵向力;Fyi表示轮胎的侧向力;αi表示轮胎的侧偏角;其中i=fl,fr,rl,rr。

图1 车辆动力学模型示意图
考虑到车轮的转角较小且仅前轮转向,假设后轮驱动力大小相同,根据力矩平衡推导出车辆动力学方程[18]。
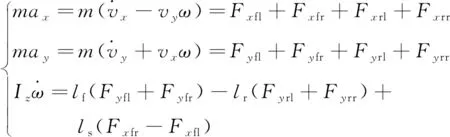
(1)
式中:m为整车质量;ω为车辆横摆角速度;Iz为整车横摆转动惯量;ax、ay分别为车辆的纵向加速度和侧向加速度。
对应的轮胎垂直载荷计算如下:

(2)
式中:h为车辆质心距地面的高度;g为重力加速度。
轮胎侧偏力为:

(3)
kf与kr分别为前后轴车轮的侧偏刚度。考虑同轴轮胎的侧偏角相同且线性轮胎的情况,则有:
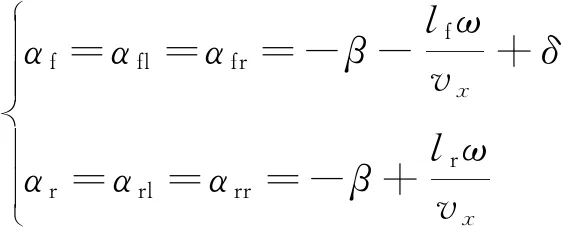
(4)
式中:αfl和αfr分别为前轴左轮和右轮的侧偏角;αrl和αrr分别为后轴左轮和右轮的侧偏角。
当不考虑轮胎非线性时,则可以得到线性车辆模型:
(5)
车辆质心侧偏角β与横向速度vy之间的关系可表示为:
(6)
1.2 差动转向系统的动力学模型
图2为差动转向系统模型结构示意图。轮毂电机驱动车辆的左右车轮可产生不同的驱动力,车轮会向驱动力较小的一侧偏转,从而实现差动转向。图2中,轮胎中心面与主销在地面的投影点之间存在一个距离r,且对于同一辆车来说,左右两侧的r相等。由于这个r的存在,使得左右转向轮轮胎纵向力Fxfl,Fxfr会产生绕各自主销的力矩τ1,τ2。其中τ1=Fxfl·r、τ2=Fxfr·r。

图2 差动转向系统模型结构示意图
当车辆需要转向时,系统根据驾驶员转动的方向盘转角发送指令控制左右前轮的驱动力矩,通过改变左右车轮力矩差实现差动驱动转向的功能。
建立如下差动转向动力学方程:
(7)
式中:Je表示转向系统的等效转动惯量;be表示转向阻尼;ΔM表示两前轮绕主销的力矩之差;τa表示回正力矩;τa=k1Fyf,k1=l2/3;l为轮胎接地半宽;τf表示转向系统的摩擦力矩。
定义同轴左右两轮绕主销的力矩差ΔM如下:
ΔM=τ2-τ1=(Fxfr-Fxfl)r
(8)
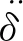
(9)
又因为轮胎力Fi=Ti/Rc,可得:
(10)
式中:Ti为车轮的转矩;Rc为车轮半径;ΔT为车辆左右前轮驱动力矩差值。
联立等式(3)(4)(9)(10),则差动转向动力学方程可改写为:
(11)
1.3 参考模型
为便于分析分布式驱动差动转向汽车的横向稳定性控制,选用2自由度线性车辆动力学模型进行研究。
参考车辆2自由度模型方程为:
(12)
设状态空间变量xd(t)=[βd,ωd]T,系统输入为前轮转角δfd,即ud(t)=[δfd],则参考模型相应的状态方程为:
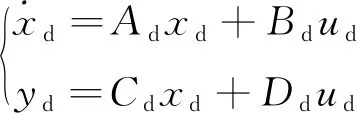
(13)
根据车辆质心侧偏角β与横向速度vy之间的关系,得到参考的侧向速度:
vyd=vxd·tanβd
(14)
由此计算出的理想质心侧偏角、横摆角速度和侧向速度即为驾驶员期望的行驶状态。
2 分层控制系统的设计
针对分布式驱动差动转向汽车,本文设计了如图3所示的分层控制系统。其中,上层控制器就是通过滑模变结构控制获得实现差动转向所需的力和力矩,以使其纵向速度、侧向速度、横摆角速度以及前轮转角跟踪上参考模型。下层控制器则以轮胎负荷率最小为目标函数将力和力矩进行优化,合理地分配给4个车轮。

图3 分层控制系统结构框图
滑模变结构控制是一种鲁棒性很强的控制方法,有着快速响应、对外界变化扰动不敏感等优点,通过指数趋近律的控制可以有效降低系统的抖动[19],因此上层控制器的设计采用了滑模变结构控制器。依据前文中建立的差动转向车辆模型和参考模型,设定纵向速度与目标纵向速度的跟踪误差;侧向速度与目标侧向速度的跟踪误差;横摆角速度与目标横摆角速度的跟踪误差;差动转向车辆车轮转角与参考输入的车轮转向角的跟踪误差分别为e1、e2、e3、e4。
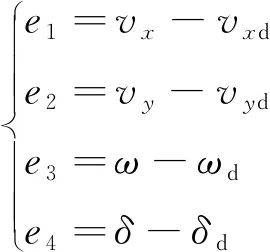
(15)
对纵向速度、侧向速度、横摆角速度和车轮转角的控制分别选取不同的滑模面:
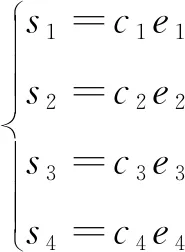
(16)
式中:c1、c2、c3、c4为须满足Hurwitz条件的控制器参数,其值均大于零。
采用指数趋近律的方法以降低系统抖动,表达式如下:

(17)

(18)
为了减小系统的抖振,将式(18)中的sgns替换成饱和函数sat(s/V),如下式:

(19)
式中:Δ为边界层,其值越大越能削弱抖振但同时趋近速度会减慢。
联立式(15)—(19),可求解出滑模控制器的输出,即所需的合力和合力矩:
(20)
3 下层控制器的设计
在下层控制器中需依据一定的性能指标或目标函数,将上层控制器求出的期望合力及合力矩最优地分配给4个车轮。
3.1 目标函数
考虑到轮胎负荷率表征了轮胎的稳定裕度,且轮胎负荷率越低,稳定裕度越大,车轮所能产生的用于驱动或转向的作用力越大,则车辆越稳定[20]。所谓轮胎负荷率是指单个车轮与地面所产生的附着力与当时路面条件下所能产生的最大附着力的比值。因此本文提出以轮胎负荷率最小为优化目标,即以4个车轮的纵向力与侧向力的平方和除以摩擦因数乘车轮垂直载荷的平方作为优化目标函数[21],如下式所示:
(21)
式中:μi为轮胎所处路面的附着系数。轮胎负荷率的取值范围为[0,1],负荷率越小,表明轮胎还能输出更多力矩,稳定裕度就越大;若负荷率的值越接近1,表明轮胎能输出的力矩余量越小,即车辆的可控性越差;当负荷率为1时,表明轮胎已达到其附着能力的极限,若此时车辆受到干扰,就会失去稳定,因为轮胎已没有剩余的力矩来对此扰动做出响应。
3.2 约束条件
3.2.1轮胎合力约束
一般情况下,每个车轮的轮胎附着极限应视为约束条件,可以用摩擦圆的概念来描述。在不考虑车身随动坐标系的情况下,可以将轮胎纵向力和侧向力计算为总的轮胎合力。轮胎合力应位于以μFz为半径的附着圆内,即:
(22)
3.2.2附着圆限制
本文将非线性附着圆约束简化为线性多边形约束。为保证各轮轮胎力的纵、横向力不超过附着圆,设立一个安全附着圆,即给式(22)中的附着圆乘以一个安全系数为0.9,之后在此安全附着圆上外接一个八边形,得到所需的线性约束,如图4所示。

图4 轮胎附着圆线性约束示意图
图4中,附着圆半径R=μFz,八边形的外接圆半径R*计算如下:
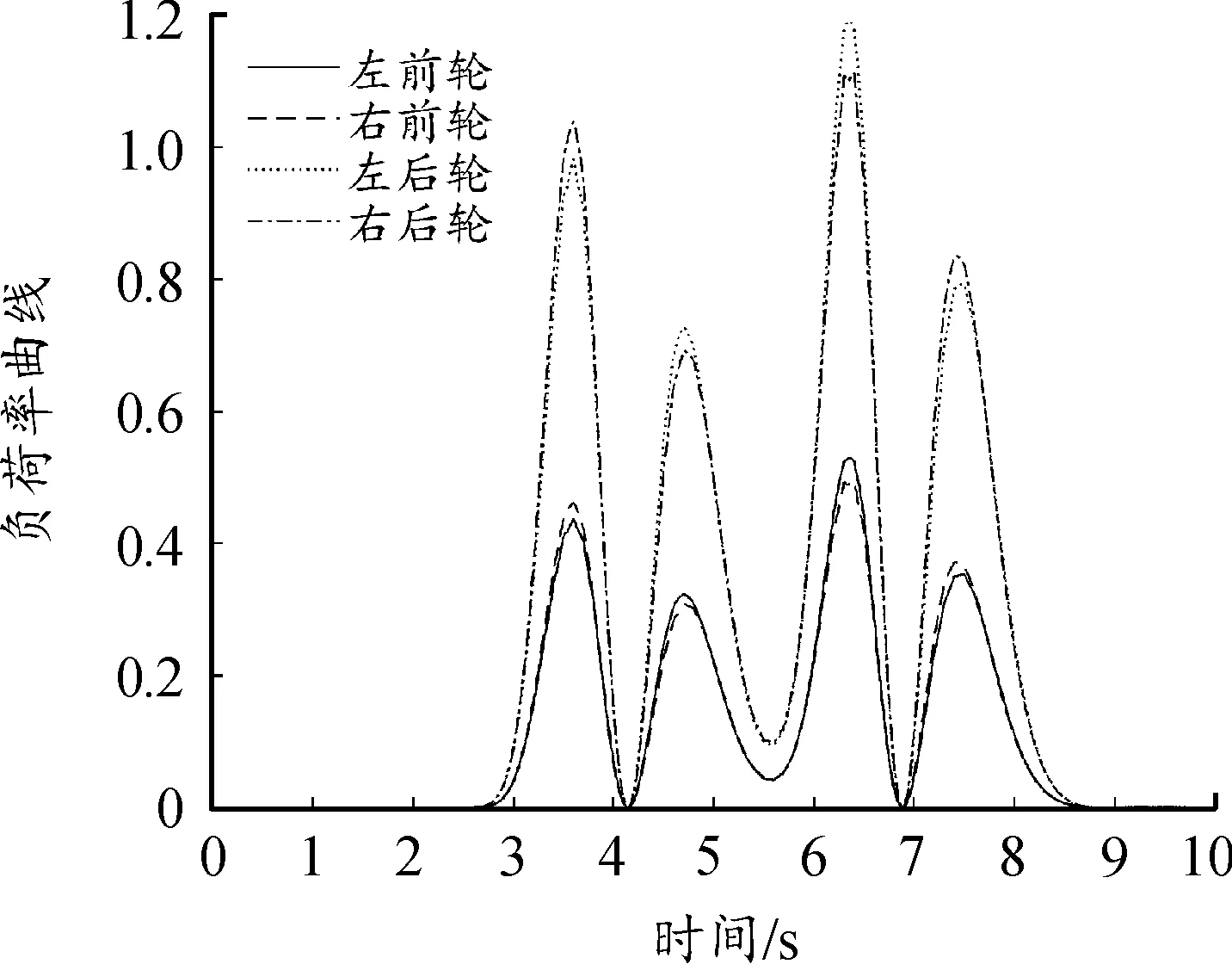
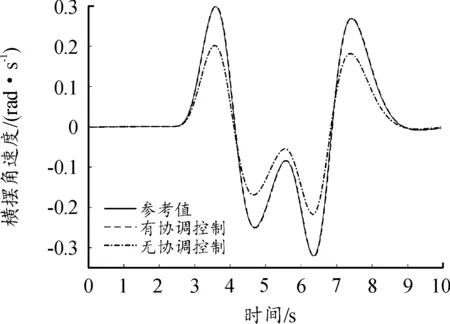
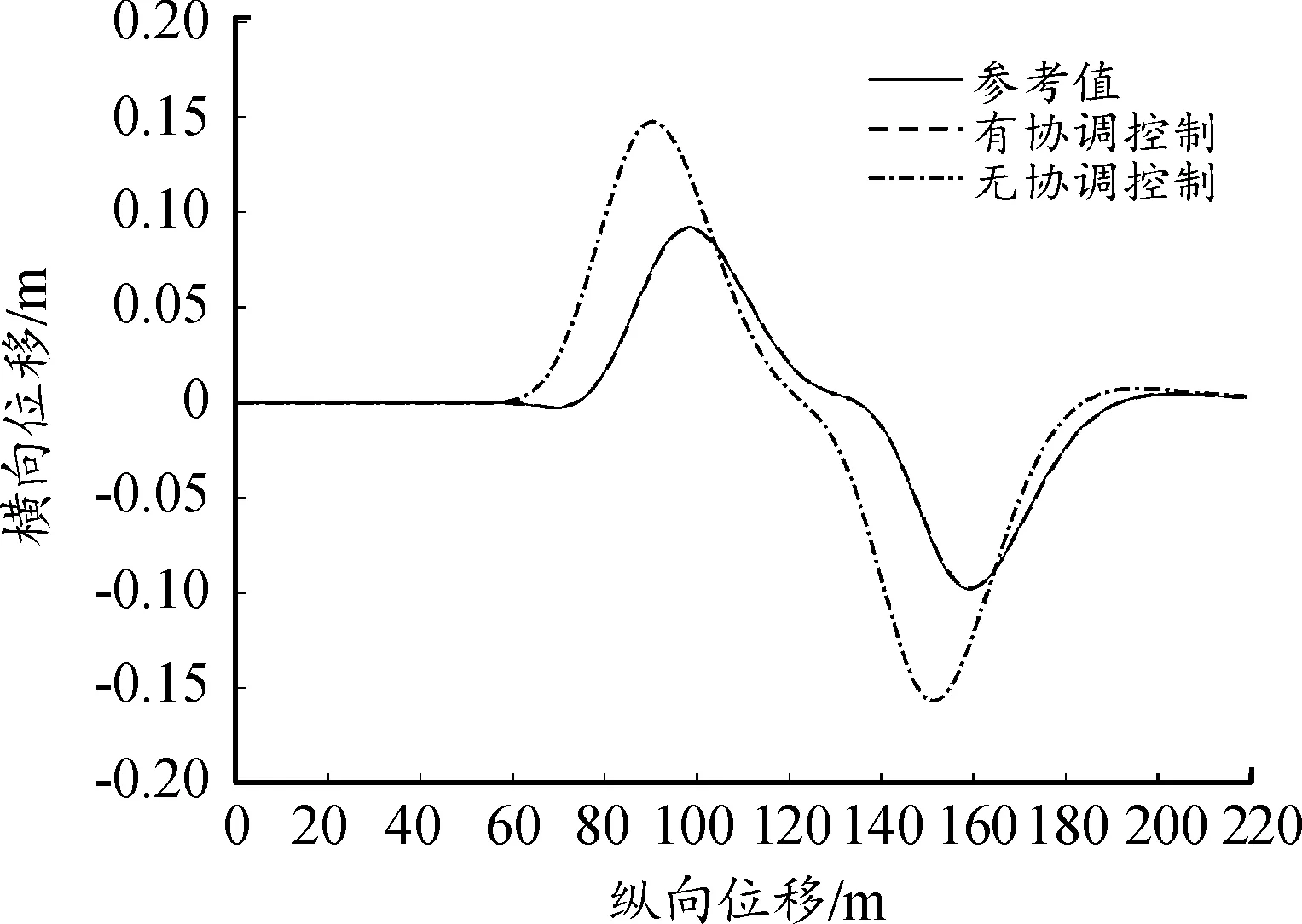
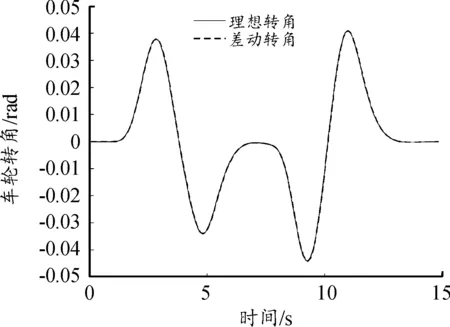
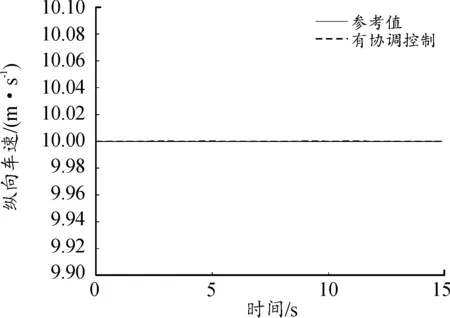
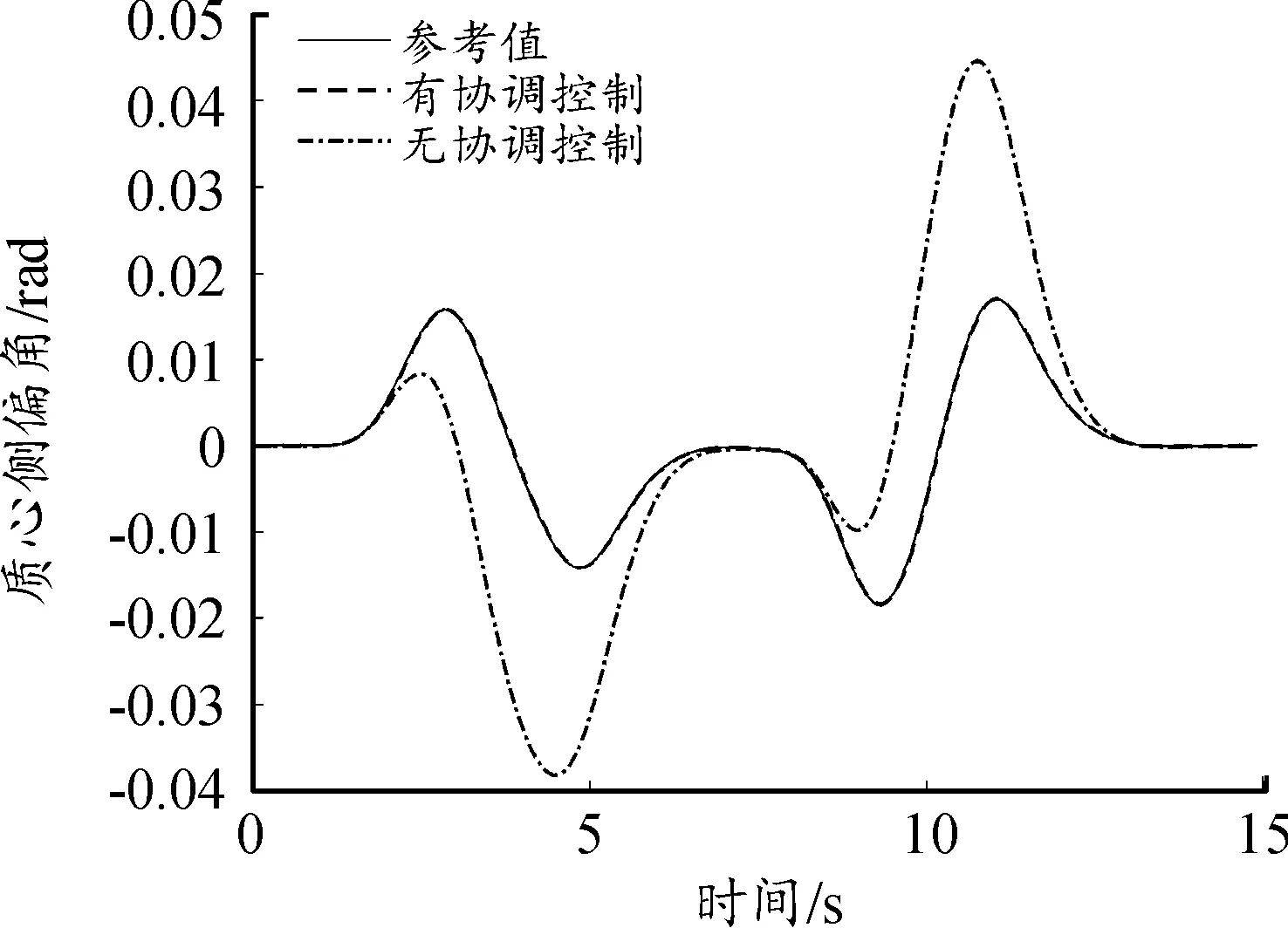
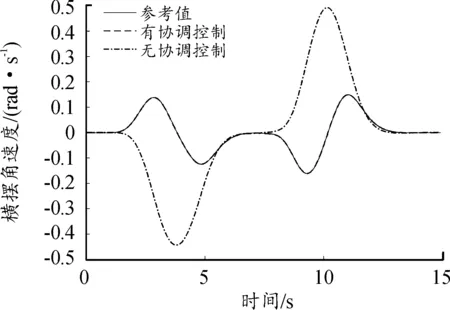
R*=0.9R·sec22.5°≈0.97R (23) 因为八边形外接圆的半径R*小于轮胎附着圆半径,因此每个轮胎力都在轮胎附着极限约束内,其具体的线性约束方程为: (24) 3.2.3电机驱动力限制 本文采用的是分布式驱动电动汽车,各轮转矩由轮毂电机单独控制,故存在最大驱动力的限制。因此,轮胎提供的纵向力限制如下式: -Tmax/Rc≤Fxi≤Tmax/Rc (25) 式中:Tmax为电机最大转矩,取值600 N·m。 上层控制器所输出的期望合力、合力矩须由各个车轮的纵、横向力提供,从而可以得到合力及合力矩约束条件: (26) 综合上述的优化目标函数和约束条件的式(21)(22)(24)(25)(26),建立优化分配算法。 优化问题是一个典型的非线性控制问题。由于本文同时存在等式与不等式的约束条件,而二次规划属于非线性规划,可以很好地对复杂问题或带有等式约束以及不等式约束的问题进行最优化求解[22],故选择二次规划方法用以求解目标函数。 二次规划的标准形式为: (27) (28) 式中的二次项系数矩阵H和一次项系数矩阵fT可以由目标函数式子转化而来,系数矩阵中的A、b、Aeq、beq、lb、ub均可由约束条件中相应的计算式转化而得,在Matlab/Simulink中编译S函数,调用quadprog函数即可求解优化问题,由此可计算得出各个车轮所需提供的纵向力和横向力。 为验证分布式驱动差动转向车辆的纵横向力协调控制器的有效性,分别针对高速高附着路面和低速低附着路面工况对有、无协调控制的差动转向车辆进行了对比仿真试验。其中,无协调控制的差动转向车辆的纵向力分配与有协调控制的相同,以满足相同的转向与纵向行驶需求,所不同的是无协调控制车辆的横向力采用四轮平均分配。 仿真时用到的车辆参数为:m=1 240 kg,h=0.54 m,g=10 m/s2,be=100 N,l=0.036 8 m,r=0.075 4 m,Rc=0.298 m,Iz=1 343 kg·m2,lf=1.04 m,lr=1.56 m,ls=0.74 m。 当路面附着系数为0.8时,kf=95 202×2 N/rad,kr=63 947×2 N/rad;当路面附着系数为0.2时,kf=68 000×2 N/rad,kr=59 000×2 N/rad。 为模拟车辆在高附着路面上高速行驶时变道的情况,设置了高速高附着双移线工况[23]。设路面附着系数为0.8,纵向车速vx=80 km/h保持不变,参考车辆的转向传动比取值为21,理想方向盘转角输入如图5所示,仿真结果如图6—12所示。 图5 方向盘转角输入曲线 协调控制器求解出的左右前轮纵向力存在差值,在此纵向力差值的作用下,车辆左右前轮实现差动转向。转向过程中的前轮转角与理想转角如图6所示。从图6中可看出,其前轮转角与理想转角近似相等且误差极小。 图6 前轮转角曲线 图7为双移线试验时有协调控制车辆的纵向速度曲线。从图7中可知,在纵向速度滑模控制器的作用下,即使车辆开始转向,纵向车速也能很好地维持在80 km/h,几乎没有出现抖振与减速等现象。 图7 纵向车速曲线 从图8和图9的轮胎负荷率曲线可知,无协调控制车辆的轮胎最大负荷率为1.19,已经超过了轮胎附着能力的极限。可知路面所能提供最大的附着力已无法满足无协调控制车辆稳定行驶,而有协调控制车辆的轮胎最大负荷率经优化后为0.81,可知轮胎仍具有一定的稳定裕度,可使轮胎与路面保持稳定的附着关系。 图8 有协调控制的轮胎负荷率曲线 图9 无协调控制的轮胎负荷率曲线 从图10的质心侧偏角曲线可知,有协调控制车辆的质心侧偏角响应明显好于无协调控制的,两者与参考值的最大偏差分别是0.000 2 rad和0.007 rad。这表明协调控制器可将差动转向车辆的质心侧偏角与参考值的误差控制在极小的范围内。从图11的横摆角速度曲线可知,无协调控制车辆的横摆角速度与参考值存在较大偏差,在仿真时间为6.4 s时,偏差值达到0.1 rad/s。而有协调控制车辆的横摆角速度响应效果很好,与参考值曲线非常吻合。 图10 质心侧偏角曲线 图11 横摆角速度曲线 图12为车辆的行驶轨迹曲线。尽管分配了相同的差动力矩用于实现车辆前轮的差动转向,但由于无协调控制车辆的轮胎负荷率未得到优化,其轮胎储备附着小,无法与路面保持稳定的附着关系,因此车辆易失稳。 图12 车辆行驶轨迹曲线 导致其质心侧偏角与横摆角速度都无法很好地跟踪参考值,行驶轨迹也就不能很好地跟踪理想轨迹。相比之下,有协调控制车辆的轮胎负荷率低,轮胎储备附着系数大,轮胎可与路面保持良好的附着,因此其各方面的响应曲线都能很好地跟踪参考值,且与理想行驶轨迹非常吻合,达到了预期的操纵效果。 针对车辆在路面附着系数较低的路面行驶容易失稳的情况,设置了低速低附着双移线工况,以验证协调控制器的控制效果。设路面附着系数为0.2,纵向速度vx=36 km/h保持不变,参考车辆模型的方向盘转角输入如图13所示,仿真结果如图14—20所示。 图13 方向盘转角输入曲线 图14为差动转向过程中的前轮转角与理想转角曲线。可知其与理想转角近似相等且误差极小。 图14 车轮转角曲线 从图15的纵向车速情况分析可知,即使在低附着路面,有协调控制车辆的纵向车速仍能稳定跟踪参考车速36 km/h。 图15 纵向车速曲线 从各项对比图中可以看出,无协调控制车辆的各方面性能响应曲线与参考值偏差很大。从图16与图17的轮胎负荷率曲线可知,其最大轮胎负荷率达到了1.08,可知轮胎与路面无法保持良好的附着关系。而有协调控制车辆的最大轮胎负荷率为0.77,轮胎还有一定的稳定裕度,可使轮胎与路面保持良好的附着关系。且有协调控制的轮胎负荷率相比于无协调控制的,整体分布更为均匀,这也说明了以轮胎负荷率为优化目标的合理性。图18为质心侧偏角曲线,在仿真过程中,无协调控制车辆的质心侧偏角严重偏离参考值,与参考值的最大偏差值达到了0.03 rad,相比之下,有协调控制车辆的质心侧偏角与参考值非常接近。同样地,图19所示的横摆角速度曲线也表明了协调控制器的有效性。无协调控制车辆的横摆角速度与参考值最大偏差达到了0.517 rad/s,而有协调控制车辆的横摆角速度与参考值非常吻合。 图16 有协调控制的轮胎负荷率曲线 图17 无协调控制的轮胎负荷率曲线 图18 质心侧偏角曲线 图19 横摆角速度曲线 图20的车辆行驶轨迹曲线反映出:无协调控制车辆的行驶轨迹与理想轨迹产生了严重的偏移。在仿真时间为9 s时,其最大横向偏移量达到了0.62 m 。有协调控制的车辆即使在低附着路面,也能保持很好的轨迹跟踪性能,可以稳定完成双移线工况的操作。 图20 车辆行驶轨迹曲线 以上仿真试验的结果验证了所设计的协调控制器在不同车速以及路面的工况下,都能有效地控制分布式驱动差动转向车辆满足行驶需求。 1) 针对分布式驱动差动转向车辆在行驶过程的纵横向特性研究,建立了差动转向车辆与参考车辆模型,提出了分层式协调控制方法。上层控制器采用滑模变结构控制求得车辆跟踪参考模型所需的总的纵横向力与合力矩;下层控制器以轮胎负荷率最小化为目标函数计算出分配给每个车轮的纵向力与横向力。随后进行了仿真试验,通过对无协调控制的车辆做对比仿真,验证所提的协调控制器效果。 2) 选取了高速高附着、低速低附着工况进行仿真试验。即使给无协调控制车辆的前轮分配了与有协调控制车辆相同的差动力矩,达到了相同的前轮转角,但由于没有对其轮胎负荷率进行优化,导致轮胎无法为车辆的行驶提供足够的稳定裕度,其各方面的响应曲线都与参考值存在较大偏差。相比之下,在协调控制器的作用下,分布式驱动差动转向车辆的轮胎力得到了合理的控制分配,纵向车速、质心侧偏角、横摆角速度和行驶轨迹都可以很好地跟踪参考值。 试验表明,所设计的协调控制器,有效地协调了车辆纵横向力之间的耦合关系,全面提升了分布式驱动差动转向车辆的动力学性能,在保持车辆纵向速度的同时,有效地保证了车辆的横向稳定性。
3.3 优化问题求解
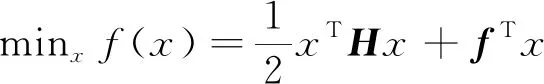

4 仿真结果分析
4.1 高速高附着路面





4.2 低速低附着路面双移线




5 结论
