变道过程非线性模型预测轨迹跟踪控制

卢 静,金智林

(1.南京航空航天大学金城学院， 南京 200016；2.南京航空航天大学 能源与动力学院， 南京 200016)

0 引言

据统计，由人为因素造成的交通事故占比高达90%，是造成道路交通事故最主要的原因[1]。但是调查数据表明，通过主动转向变道防碰撞，能够降低近40%的追尾事故的发生[2-3]。因此，如何实现车辆自主安全的、可靠的跟踪变道轨迹进行避障，是降低交通事故的发生率，实现车辆智能化的关键问题。

目前，国内外对汽车主动避障技术的研究首先由上层控制考虑，基于车-车间的位置关系动态求解车辆在当前采样时刻的理想控制参数[4-5]；再由下层控制从上述算法中确定的车辆目标减速度等参数考虑，实现对制动、转向等下层执行机械部件的精确控制[6-7]。在横向控制领域，Zhang等[6]提出了一种考虑驾驶员转向特性的主动后转向车辆路径跟踪控制方法，基于驾驶员模型参数辨识，建立了MPC控制器设计的驾驶员模型和车辆模型，设计全局目标函数以优化驾驶员-车辆系统的整体性能，显著提高了系统性能。Li等[7]基于转向决策序列构造了预测期内轮胎状态刚度的变化趋势，提出了一种调整轮胎状态刚度的方法来解决线性化过程中的抖动问题，设计了线性时变模型预测控制器，显著提高车辆在极端条件下的稳定性。吉岩等[8]提出了基于驾驶员转向过程中的预瞄及滚动优化行为的控制方法，并基于veDYNA进行了验证。然而，上述研究普遍基于线性模型进行避障轨迹跟踪控制器设计，且未考虑路面附着系数变化导致的非线性动力学耦合关系。当车辆处于中高速或紧急工况时，侧向加速度较大，若此时路面附着系数变化会加剧轮胎侧偏特性对车辆动力学的影响，系统将呈现强非线性。此外，目前广泛采用的模型预测控制算法需要在每个采样时刻对模型进行动态优化求解，这对运算实时性即非线性模型构造时的复杂度同样提出了更高的要求。因此，需要针对变道过程中路面附着系数变化带来的模型非线性问题以及滚动优化算法对于实时性的要求，设计避障轨迹跟踪算法。

针对上述问题，本文建立了整车动力学模型、驾驶员模型和主动转向系统模型，提出了考虑路面附着系数动态变化的变道过程非线性模型预测轨迹跟踪控制策略，针对变道过程中路面附着系数变化带来的模型非线性问题以及滚动优化算法对于实时性的要求，构建了非线性变道轨迹跟踪模型及其滚动时域优化求解方法，并通过硬件在环试验对本文提出的算法在高附着路面和低附着路面下的有效性进行了验证。

本文的主要贡献在于：

1) 针对横向避障系统中最为关键的变道轨迹跟踪问题，提出了考虑路面附着系数变化的变道过程非线性模型预测轨迹跟踪控制策略设计方法。

2) 针对变道过程中由于路面附着系数变化带来的模型非线性问题以及滚动优化算法对于实时性的要求，构建了非线性变道轨迹跟踪模型，并提出了滚动时域优化求解方法。

1 动力学建模

本文主要对汽车在执行轨迹跟踪任务时的系统动力学特性进行研究。在整车动力学层面，将整车简化为二自由度的车体模型[9-10]，其运动微分方程为：

(1)

主动避撞过程中的轨迹跟踪功能的实现主要依赖转向系统。主动转向模型包括转向盘与转向轴、双行星齿轮系、齿轮齿条和转向电机四个部分[11-12]。通过双行星齿轮系可在驾驶员输入转角的基础上添加附加转角，不仅可以在无人驾驶模式下实现自动转向，而且可以在有人驾驶时为驾驶员提供附加转角。其中，转向轴与转向盘模型系统的动力学方程为：

(2)

式中:Ka为转矩传感器扭杆刚度系数；Ja为转向盘的转动惯量；θs1为转向盘转角；Ba为转向盘的阻尼系数；θs2为输入太阳轮转角；Te为转矩传感器输出转矩；Tb为驾驶员输入转矩;fa为转向轴与转向盘的库仑摩擦力常数。

通过对双行星齿轮的各部分的力矩传递特点分析和运动特点分析[13]，可以得到下面的运动学关系式：

(3)

对齿轮齿条进行动力学分析，得到如下表达式：

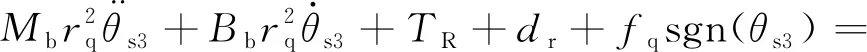
Td2+GamTa

(4)

式中:TR为等效到转向柱上的轮胎回正力矩；dr为等效到转向柱上的路面随机干扰力矩；fq为转向柱上的库仑摩擦力常数。

转向电机模型如式所示[14]：

(5)

式中:La为转向电机电感；ia为转向电机电流；Ra为转向电机电阻；Ua为转向电机两端电压；Ea为转向电机反电动势；Ke1为转向电机反电动势常数；ωa为转向电机转速，Tam为转向电机电磁转矩；Bam为转向电机阻尼系数；Jam为转向电机的转动惯量；fam为转向电机转子处库仑摩擦力常数；TL为转向电机负载转矩；Gam为转向电机减速机构减速比；θam为转向电机转角;Kt为电磁转矩常数。

2 考虑路面附着系数变化的变道过程轨迹跟踪控制

本节首先针对变道过程中由于路面附着系数动态变化带来的模型非线性问题以及滚动优化算法对于实时性的要求，构建了非线性变道轨迹跟踪模型及其滚动时域优化求解方法。在此基础之上，提出了非线性模型预测控制变道轨迹跟踪控制策略。

2.1 问题描述

在无人驾驶汽车跟踪规划轨迹的时候，通常以下述的方式进行跟踪控制：在给定的直角坐标系中，跟踪车辆需要由一个已知给定的初始状态出发，其中已知给定的初始状态可以存在于轨迹之上或存在于轨迹之外[15-16]。无人驾驶汽车的轨迹跟踪过程可通过图1来表示，理想轨迹由一条光滑的曲线给出，该轨迹意为一条几何曲线f(xr(t))，其中自变量xr是时间t的函数，该曲线方程是时间t的隐函数。

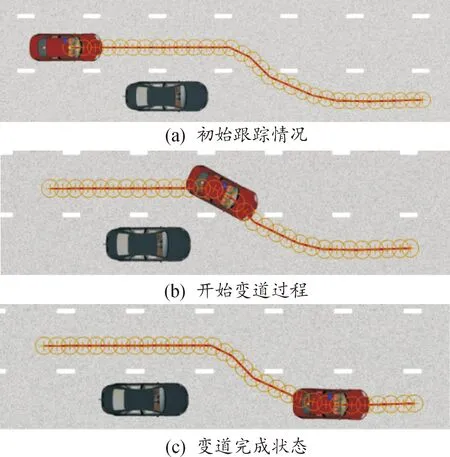
图1 变道状态过程示意图

基于上述分析，得到考虑车辆行驶区域的路面特征、路面摩擦因数以及车辆位置和内部状态的跟踪轨迹流程，如图2所示。利用MPC控制器对规划出来的轨迹分割各个数据点进行依次跟踪，并且采用循环优化的方式实现整个路径的跟踪[17]。

图2 轨迹跟踪流程框图

在上述轨迹跟踪控制的过程中，控制器需要根据理想轨迹与实际轨迹间的偏差，计算当前理想前轮转角，根据Pure Pursuit算法，轨迹偏差与理想前轮转角间的函数关系如式所示。

(6)

式中:δi为理想前轮转角；L为前后轴距；e为实际轨迹与理想轨迹间的误差；vx为车辆纵向速度；kv为调整系数。

然而，路面附着系数的不同，会导致该函数关系呈现非线性特性，需要根据路面附着系数的变化对控制策略进行修正，从而使被控车辆能够更好的跟踪理想轨迹。

2.2 考虑路面附着系数的轨迹跟踪目标及约束

对于非线性系统轨迹跟踪求解问题，一般采用如下的离散模型[18]：

ξ(t+1)=f(ξ(t),u(t))

ξ(t)∈Χ,u(t)∈Γ

(7)

式中：f(·,·)表示为系统的状态转移函数；ξ为ns维状态变量；u为mc维控制变量；Χ为状态变量约束；Γ为控制变量约束。

要实现在轨迹跟踪过程中考虑路面附着系数的影响，首先要实现对路面附着系数的实时动态估计。综合考虑计算实时性和估计准确度，基于卡尔曼滤波算法构建轨迹跟踪过程中的路面附着系数估计器，如式所示：

xf(k)=Afxf(k-1)+Bfuf(k)+wf(k)

zf(k)=Hfxf(k)+yf(k)

(8)

式中：xf(k)为k时刻的路面附着系数估计模型的状态量；uf(k)为控制量；wf(k)为过程噪声；zf(k)为k时刻路面附着系数的观测值；yf(k)为测量噪声；Af、Bf、Hf为系统参数。

为了消除和削弱测试过程中的异常观测方差对路面附着系数参数估计的影响，同时考虑到在增加自适应环节后对滚动优化环节算力带来的要求，设状态一步预测向量的误差方程为：

(9)

观测向量的误差方程为：

(10)

构造如下极值原则：

(11)

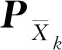
得到自适应附着系数估计器，如式(12)所示：

(12)

下面，基于模型预测控制策略设计考虑路面附着系数的轨迹跟踪控制器。设定f(0,0)=0为系统的控制目标，可见该点同时也是系统的一个稳定点。此时对于任意的时域N的优化目标可表示为式(13)。

JN(ξ(t),zf(k),U(t))=

(13)

式中：U(t)=[u(t),…,u(t+N-1)]T是在时域N内的控制量输入序列，ξ(t)是在输入向量序列U(t)作用下状态向量轨迹，l(·,·)表示对理想值的跟踪性能优劣，P(·)表示终端约束。

为了使每个时刻都能够使该优化目标得到可行解，需要在优化目标中加入松弛因子，如式(14)所示：

J(ξ(t),zf(k),u(t-1),ΔU(t))=

(14)

式中：ρ为权重系数；ε为松弛因子。

将预测时域内的输出量偏差表示为：

(15)

通过矩阵运算，可以将优化目标调整为：

J(ξ(t),zf(k),u(t-1),ΔU(t))=

[ΔU(t)T,ε]THt[ΔU(t)T,ε]+

Gt[ΔU(t)T,ε]+Pt

(16)

2.3 模型预测轨迹跟踪控制策略

相比基本模型预测控制算法，非线性模型预测控制策略采用了精度更高的非线性模型，能够有效地克服变道过程的不确定性、非线性和并联性，并能方便地处理变道过程模型被控变量中的各种约束[19]。基于非线性模型预测控制的变道轨迹跟踪控制策略，如图3所示。

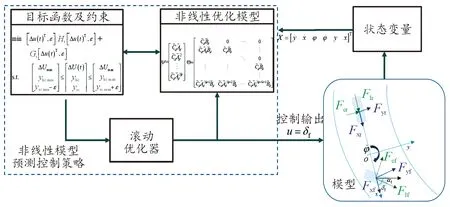
图3 非线性模型预测控制的变道轨迹跟踪控制策略示意图

非线性模型预测控制的优化模型本身即为非线性模型[20]，其优化目标、约束如式所示：

(17)

ξk+1,t=f(ξk,t,zfk,t,uk,t),k=t,…,N-1

(18)

ξk,t∈Χ,k=t+1,…,t+N-1

(19)

uk,t∈Γ,k=t,…,t+N-1

(20)

ξt,t=ξ(t)

(21)

ξN,t∈Χfin

(22)

(23)

3 试验分析

为验证本文所提出算法的有效性及准确性，建立硬件在环测试平台，如图4所示。为保证硬件在环仿真过程的实时性，基于Matlab/Simulink以及CarSim建立的控制算法模型及道路环境模型运行于NI PXI平台。

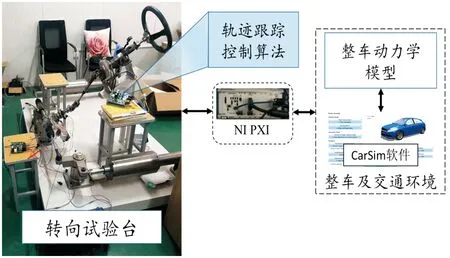
图4 试验环境示意图

3.1 跟踪轨迹仿真分析

分析不同测试车速下的理想路径跟踪情况，并将控制结果与自适应MPC进行对比，如图5所示。如果在跟踪时产生的误差较大，那么证明在跟踪控制的时候不能够很好地进行跟踪。通过图5分析可得，相比自适应MPC算法，本文提出的非线性MPC算法可降低路径跟踪误差14.35%，且非线性MPC算法可快速消除跟踪误差。

图5 轨迹跟踪曲线

进一步对比分析低附着系数下不同测试车速下的理想路径跟踪情况，如图6所示。如果在跟踪时产生的误差较大，那么证明在跟踪控制的时候不能够很好地进行跟踪，从而不能够按照期望完成轨迹跟踪控制。通过图6分析可得，相比自适应MPC算法，本文提出的非线性MPC算法可降低路径跟踪误差11.25%，且非线性MPC算法可快速消除跟踪误差。

图6 低附着系数(0.3)时的轨迹跟踪曲线

3.2 横摆角速度仿真分析

对比分析不同测试车速下的横摆角速度指标，如图7所示。较小的横摆角速度能够使汽车在行驶过程中更加稳定，如果横摆角速度过高的话会导致汽车产生侧滑或者侧翻。分析可得，相比自适应MPC算法，本文提出的非线性MPC算法可降低跟踪误差24.35%。

图7 轨迹跟踪过程中横摆角速度曲线

对比分析不同测试车速下的横摆角速度指标，如图8所示。较小的横摆角速度能够使汽车在行驶过程中更加稳定，如果横摆角速度过高的话会导致汽车产生侧滑或者侧翻。分析可得，相比自适应MPC算法，本文提出的非线性MPC算法可降低跟踪误差21.21%。

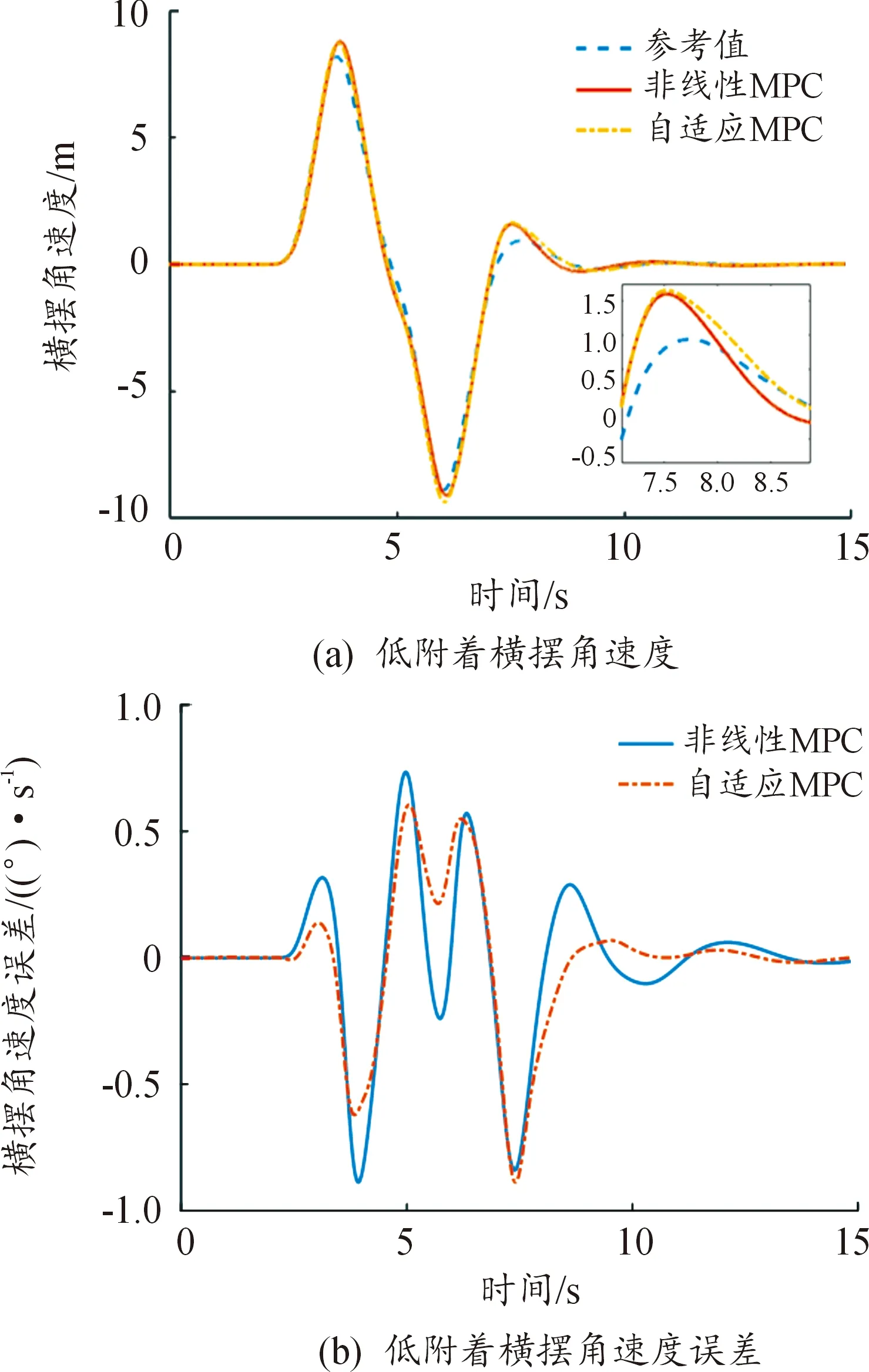
图8 低附着系数(0.3)时的横摆角速度曲线

3.3 侧向加速度仿真分析

对比分析不同测试车速下的横摆角速度指标，如图9所示。如果汽车行驶时侧向加速度过大会导致汽车在行驶过程中出现失稳的现象，因此汽车在进行变道的过程中，越小的侧向加速度汽车在行驶过程中越稳定。通过图9可得，在30 km/h低速运行的情况下，相比自适应MPC算法，本文提出的非线性MPC算法可降低波动19.67%，说明非线性MPC控制器的稳定性更好。

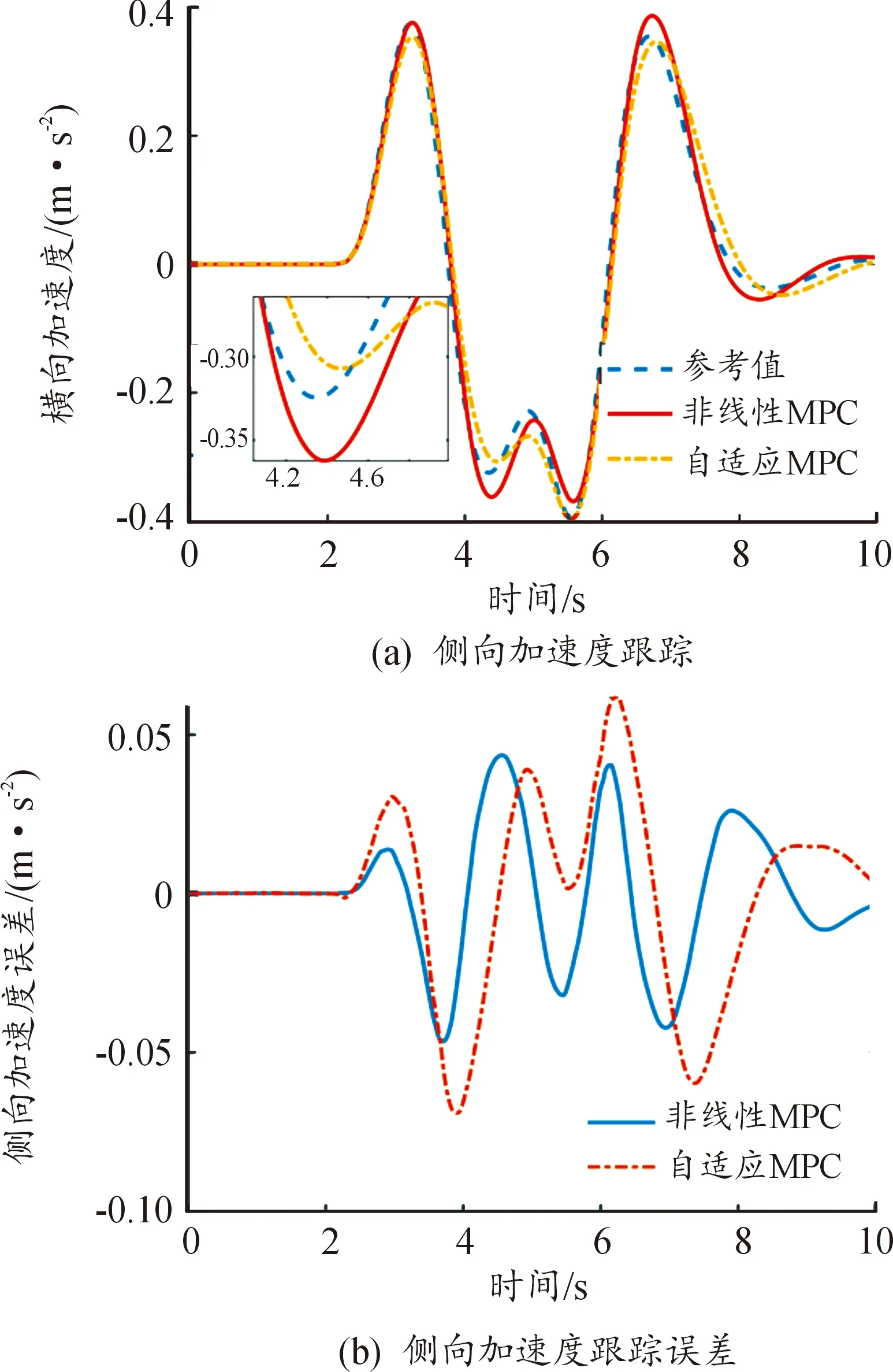
图9 轨迹跟踪过程中侧向加速度曲线

同样的，进一步对比分析低附着系数下不同测试车速下的理想路径跟踪情况，如图10所示，测试路面附着系数为0.3。对比分析不同测试车速下的横摆角速度指标，如图10所示。如果汽车行驶时侧向加速度过大会导致汽车在行驶过程中出现失稳的现象，因此汽车在变道过程中，越小的侧向加速度汽车在行驶过程中越稳定。通过图10可得，在30 km/h低速运行的情况下，相比自适应MPC算法，本文提出的非线性MPC算法可降低波动12.54%，说明非线性MPC控制器的稳定性更好。

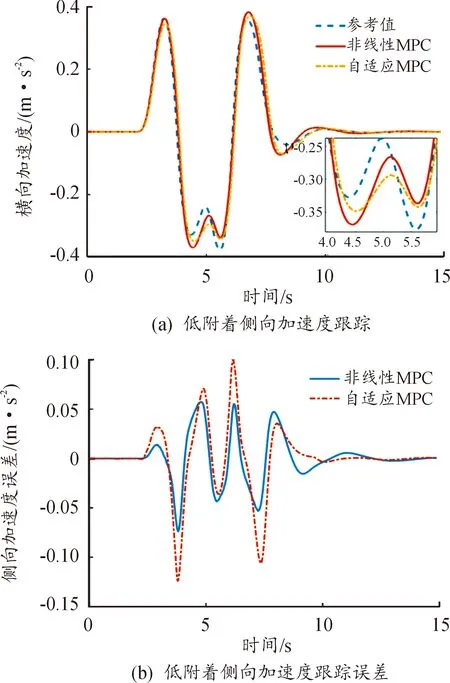
图10 低附着系数(0.3)时的侧向加速度曲线

4 结论

以汽车主动变道轨迹跟踪系统为对象，研究了汽车主动变道系统的结构和工作原理，并建立了模型。考虑路面附着系数对轨迹跟踪过程带来的影响，设计了变道过程非线性模型预测轨迹跟踪控制。仿真分析表明：与自适应模型预测控制器相比，本文提出控制策略得到的跟踪误差更小，具有更好的跟踪控制效果。