砂土粒径变化对桩体动力响应影响的试验分析

金丹丹, 赵 俣, 王炳辉, 李晓文

(1. 江苏大学 土木工程与力学学院, 江苏 镇江 212013; 2. 江苏科技大学 土木工程与建筑学院, 江苏 镇江 212100)

桩基础是一种常用的深基础形式,被广泛地应用于土木工程领域中．它具有承载力大、稳定性好、沉降值小等特点．桩通常依赖桩周土体发挥作用,因此桩-土动力相互作用问题已成为岩土工程研究的重要课题之一．目前已开展较多的桩基础抗震性能研究，地震荷载作用下桩体破坏机制分析就是基于桩土相互作用体系开展的[1]．另外,工程中较为常见的强夯等冲击荷载对桩基产生的振动问题同样属于桩-土动力相互作用问题的范畴[2]．桩基础在动荷载作用时受到荷载形式和大小、桩身自重和几何尺寸以及桩周土体特性等多方面因素的影响．因此,开展桩土相互作用体系中桩体的动力响应研究具有重要的理论意义和工程应用价值．目前研究桩基动力相互作用问题的方法主要有数值法和试验法．许四法等[3]为研究桩基埋深对桩身变形的影响,利用室内模型试验和有限元软件对此进行分析,结果表明桩基埋深对桩身变形有较大影响,桩基埋深较浅时表现出刚性桩特性,增加埋深可减小桩身变形．李丹阳等[4]采用ABAQUS有限元计算程序,建立轨道结构-路基-地基相互作用三维有限元模型,探讨列车移动荷载作用下桩身直径等参数对桩基振动的影响,研究发现桩体振动主频随桩长和桩身直径的增加呈先增大后减小的变化趋势．唐亮等[5]研究桩模量和桩径等对桩基地震响应的影响规律,研究结果表明:桩的侧向位移随着桩基模量和桩底连接刚度增加而减小;当保持桩的抗弯刚度不变时,桩的弯矩和位移随着桩径的增大而显著增加．刘涉川等[6]研究了可液化地基中劲芯复合桩的地震响应,通过参数分析探究了桩径、桩长和剪切模量等因素对可液化土-复合桩-上部结构地震响应的影响规律,并提出复合桩的抗震性能随桩径和桩长的增大而增大的结论．柳飞等[7]通过对比不同长径比条件下单桩竖向承载力和桩端阻力粒径效应的不同,研究侧摩阻力对桩基承载力离心模型试验中粒径效应的影响,研究表明单桩竖向承载力的粒径效应比桩端阻力的粒径效应显著．

目前现阶段大部分文献多从桩体本身属性出发,或考虑改变土的性质来研究桩体动力响应[8-14],而考虑桩体尺寸与砂土粒径的比值对桩体动力响应影响的研究尚鲜见报道．为此,笔者拟设计冲击荷载作用下桩-土动力相互作用的模型试验,模拟在冲击荷载作用下桩-土动力相互作用响应,分析冲击荷载作用下砂土粒径对桩体动力响应的影响．试验设计中主要针对不同桩径、砂土粒径及不同冲击荷载作用下的工况进行分析．

1 试验仪器及试验方案

1.1 试验仪器

本试验中采用自行研制的小型冲击桩-土相互作用试验测试装置,该测试装置主要由冲击系统、箱轨系统和数据采集系统组成,如图1所示．

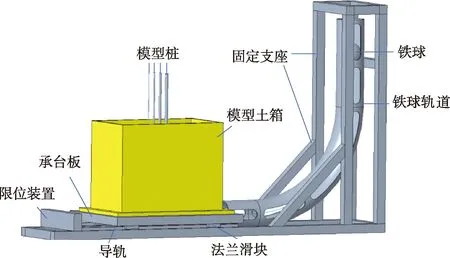
图1 小型冲击桩-土相互作用试验装置模型图

箱轨系统包括模型土箱、模型桩、铝制限位装置、铝制导轨、缓震胶垫和法兰滑块．冲击系统包括铁球、固定支座和铁球轨道．有机玻璃材质模型土箱内部尺寸(长×宽×高)为600 mm×350 mm×500 mm,壁厚为20 mm．模型土箱最大承重为300 kg．承台板材料为亚克力,台面尺寸(长×宽)为800 mm×600 mm,作为模型土箱的承台底板．铁球直径为140 mm,质量为11 kg．将桩底固定在模型土箱底部,用以反映在真实场地中桩底嵌入岩层的情况．试验所用不锈钢材质模型桩基本参数如下:桩体直径分别为5、10、15和20 mm,弹性模量为210 GPa,泊松比为0.3,密度为7.85 g·cm-3,高度为800 mm．

1.2 冲击荷载试验原理

冲击荷载试验原理是基于机械能守恒定律．铁球下落过程中与轨道间存在摩擦力,同时受铁球与箱体冲击发生变形的影响,铁球从轨道上部下落的重力势能只有部分转化为模型土箱运动的动能．机械能守恒定律表达式为

kmgh=Mv2/2,

(1)

式中:m为铁球质量,取11 kg;g为重力加速度,取值10 m·s-2;h为铁球下落高度,m;M为模型土箱和箱中所盛土的总质量,kg;v为模型土箱运动速度,m·s-1;k为势能转换系数,取经验值0.9．这是由于铁球自由下落过程中,其重力势能有所损耗,其中损耗能包括摩擦损耗、热量损耗和撞击损耗等．该处势能转换为模型土箱动能的转换效率取经验值为90%,即运动过程中有10%能量损耗.

1.3 试验材料及试样制备

试验中选用福建标准砂作为模型土,测得砂土基本物理参数如下:颗粒密度ρ=2.69 g·cm-3,最大孔隙比emax=1.063,最小孔隙比emin=0.520,相对密实度Dr=50%．本试验中各粒径范围砂的照片如图2所示．

图2 各粒径范围砂的照片

模型地基土分6次填入模型土箱中,按照相对密实度为50%将模型地基土压实,试样干密度为

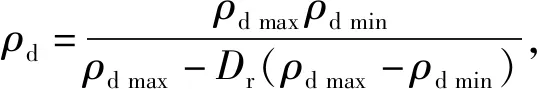
(2)

式中:ρd为试样干密度,g·cm-3;ρd max和ρd min分别为试样最大和最小干密度,g·cm-3．

根据式(2)计算出相对密实度为50%时,各粒径范围砂的干密度和用量如表1所示．表1中,总质量指的是模型土箱中高度为300 mm砂土的质量,而每次填入的砂土质量称为每次质量．

表1 不同粒径范围砂的干密度和用量

笔者针对不同砂土粒径范围(粒径范围分别为0.10～0.25、0.25～0.50、0.50～1.00和1.00～2.00 mm)和桩径(桩径分别为5、10、15和20 mm)下的桩-土相互作用冲击试验．限于本文篇幅,笔者仅对埋深为300 mm的桩体试验工况进行了分析说明．

试验量测的数据为模型桩桩顶的加速度、模型桩的应变和土体加速度．传感器分别为压电式加速度传感器(YD-182M型)和电阻应变片(BX120-3AA应变计)．由于传感器外形小巧,灵敏高,因而对整体模型结构几乎无影响．在埋置土层中的模型桩上,从桩底部向上每隔75 mm粘贴一对应变片,以观测模型桩在冲击振动过程中的应变变化情况．在模型桩的桩顶及不同深度位置的土层中布置了加速度传感器,用以分析在冲击振动过程中桩顶的加速度变化和不同位置土层的加速度响应．加速度传感器和应变片的布置示意图如图3所示．图3中,等距离布置在模型土箱底部的各个模型桩之间的距离为70 mm．

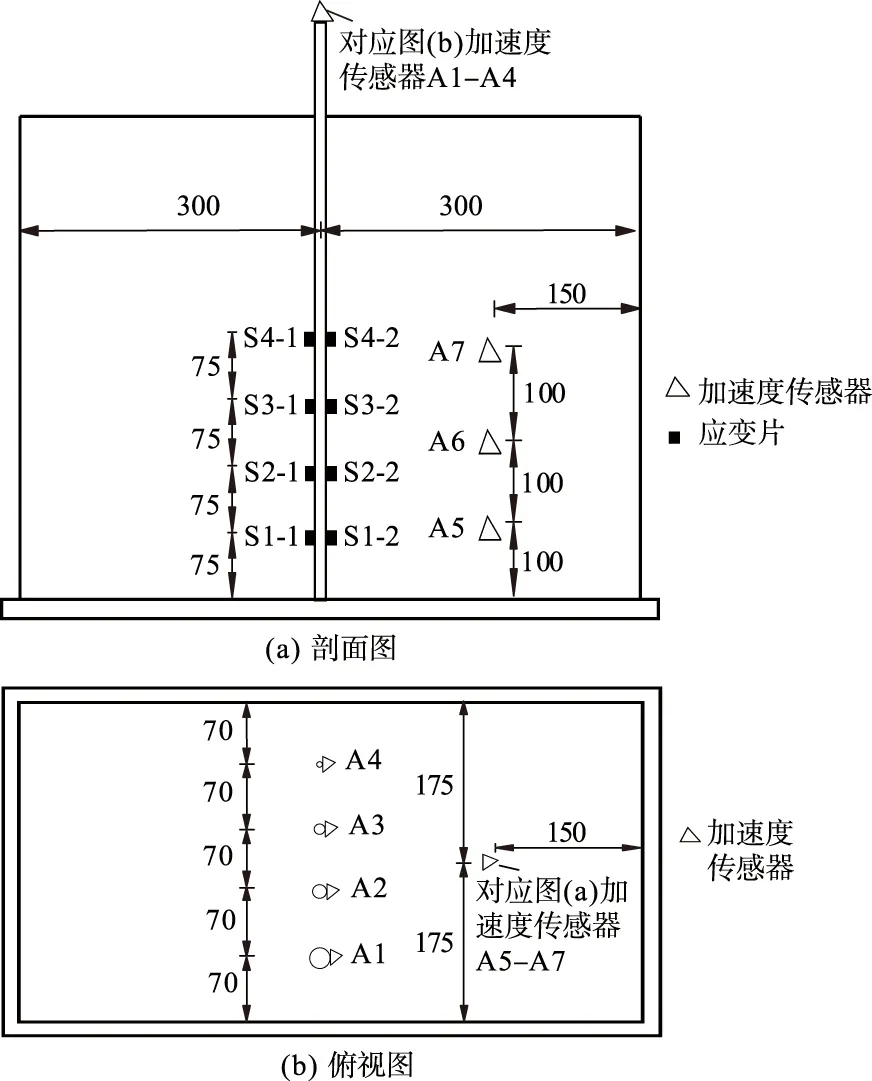
图3 传感器布置示意图(单位: mm)

2 试验结果分析

2.1 径径比值取值方法

本研究中的径径比值d桩/d砂定义为模型桩的桩径d桩与砂土颗粒平均粒径d砂的比值．不同粒径范围下径径比值随模型桩的桩径变化曲线如图4所示.

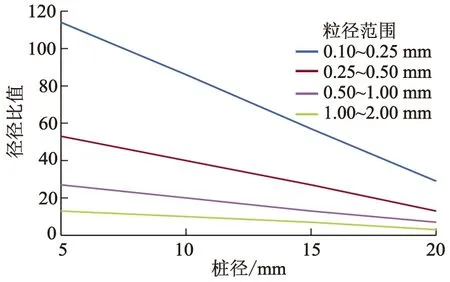
图4 不同粒径范围下径径比值随桩径变化曲线

2.2 桩顶加速度时域分析

图5为模型土箱不装土时桩径为20 mm桩体的桩顶加速度时程图，施加的冲击荷载与装土时相同．图6和图7为不同砂土粒径范围下桩径分别为20 mm和15 mm桩体的桩顶加速度时程图．限于篇幅,只给出了桩径分别为15 mm和20 mm的时程图,其余桩径时程图与其变化规律基本一致．由图5和图6a可知,装土时桩体加速度幅值较未装土时明显减小,减小约50%．

图5 桩径为20 mm时桩顶加速度时程图(未装土)

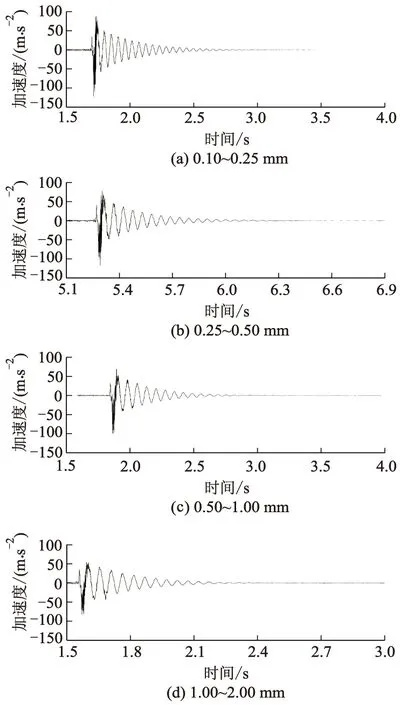
图6 不同粒径下桩径为20 mm时桩顶加速度时程图

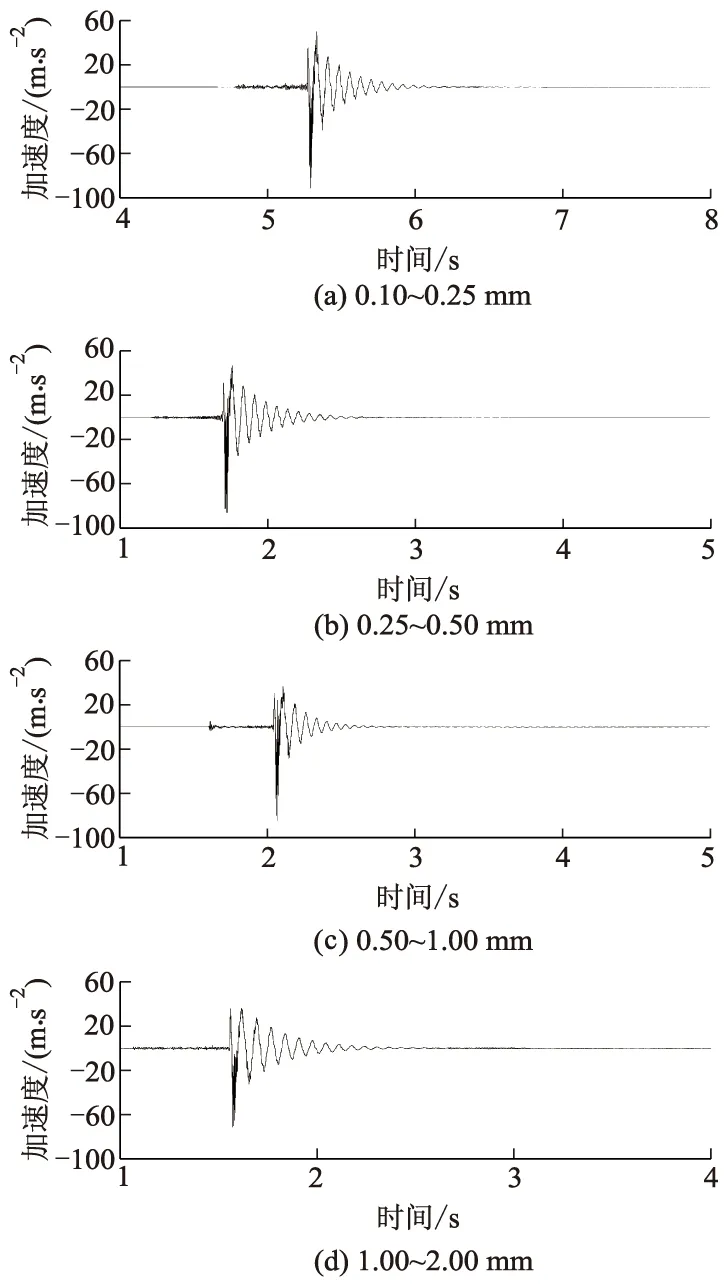
图7 不同粒径下桩径为15 mm时桩顶加速度时程图

由图6、7可知:在冲击荷载作用前期,桩顶加速度达到峰值,随后加速度幅值随时间增大而逐渐衰减;随着砂土粒径增大,桩体振动各阶段加速度幅值明显减小,加速度衰减时间有小幅减小,其中砂土粒径为0.10～0.25 mm时,桩顶加速度衰减时间为1.2 s,由开始振动至静止经历的衰减时长最长．其中衰减时长定义为从桩体产生加速度开始至加速度衰减至0的时间取值．各桩的桩顶加速度呈现出相似规律．这是因为随着砂土粒径范围的增大,桩与土的接触面积增大,桩体抵抗变形的能力增强,桩在粒径较大土体中加速度较小．

表2为大粒径(1.00～2.00 mm)下不同径径比值时桩顶加速度的衰减时间及加速度峰值汇总．图8为不同粒径范围下桩顶的加速度峰值随径径比值变化的曲线．

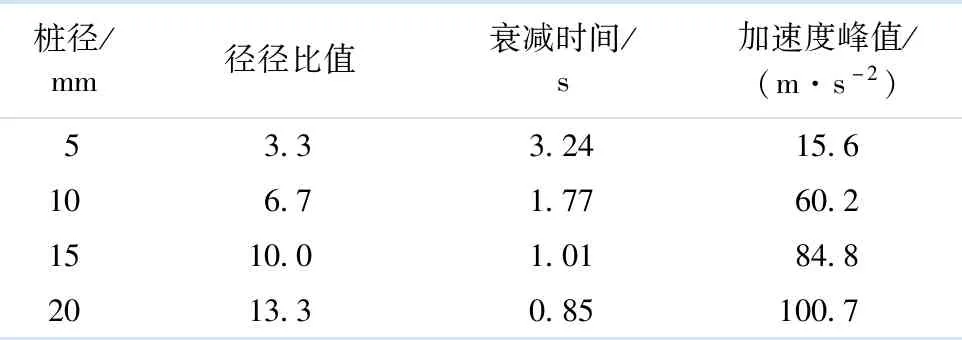
表2 大粒径下不同径径比值时桩顶加速度衰减时间及加速度峰值汇总

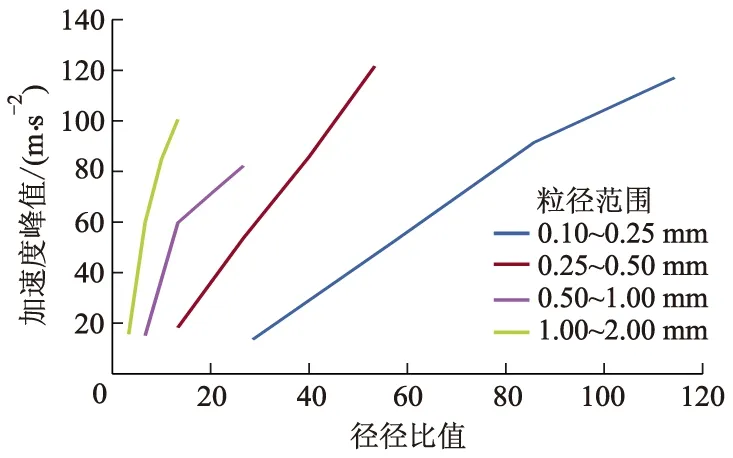
图8 桩顶加速度峰值变化曲线

由表2和图8可知:不同的粒径范围下桩顶加速度的峰值均随径径比值的增大而增大;大粒径范围(1.00～2.00 mm)下(图8中最左侧趋势线)较其他粒径范围(图8中右侧3条趋势线)情形而言，加速度峰值随径径比值增大的变化趋势线具有更大的斜率，即大粒径范围下，桩顶加速度对径径比值的变化更为敏感.

2.3 桩顶加速度频域分析

图9和图10为不同粒径范围下桩径分别为15 mm和20 mm桩体的桩顶振动加速度响应频域曲线．

图9 桩径为15 mm时不同粒径范围下桩顶振动加速度响应频域曲线

图10 桩径为20 mm时不同粒径范围下桩顶振动加速度响应频域曲线

由图9、10可知:不同粒径范围下,桩顶加速度的低频响应丰富,桩径为15、20 mm时的频率分布形式基本相同,加速度傅里叶谱幅值在频率为10～20 Hz达到了峰值;在相同的桩径下,随着砂土平均粒径增大,加速度傅里叶谱幅值随着粒径的增大而增大,粒径范围最大(1.00～2.00 mm)时,加速度傅里叶谱幅值达到最大值;同一频率区间内,随着砂土平均粒径的增大,加速度频谱的谱宽逐渐变窄．

2.4 桩身应变反应分析

试验测量桩身应变的位置在距桩底15 cm处,该位置处于桩的中心位置,能够较好地反映桩身的弯曲应变规律．图11和图12为桩径分别为15、20 mm时不同粒径范围的桩身弯曲应变时程图,其余桩径的桩身应变时程图与其变化规律基本一致．由图12可知:在不同粒径范围的桩身弯曲应变时程曲线形状大致相同,即受到冲击荷载后桩身弯曲应变迅速达到峰值,而后桩身弯曲应变反而逐渐衰减．

比较图11、12可知,桩径不变时,桩身弯曲应变随着砂土粒径增大而减小,桩身弯曲应变衰减变快．可见,在粒径为0.10～0.25 mm时,桩身变形最大,振动时间最长．

图13为不同粒径范围下桩身应变峰值随径径比值变化的曲线．由图13可知:桩身应变峰值随径径比值增大而减小;桩体在细砂(0.10～0.25 mm)中的变形明显大于其他粒径范围,即同一径径比值下的应变峰值随粒径增大而减小．可见,可通过改变砂土粒径(径径比值)来控制桩体应变．

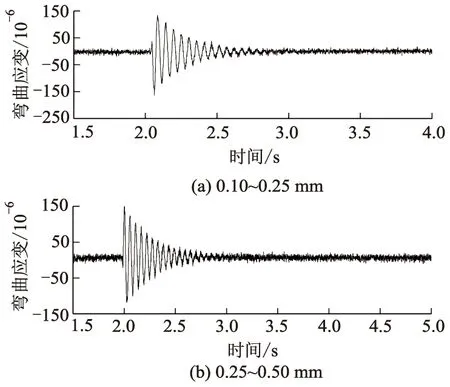
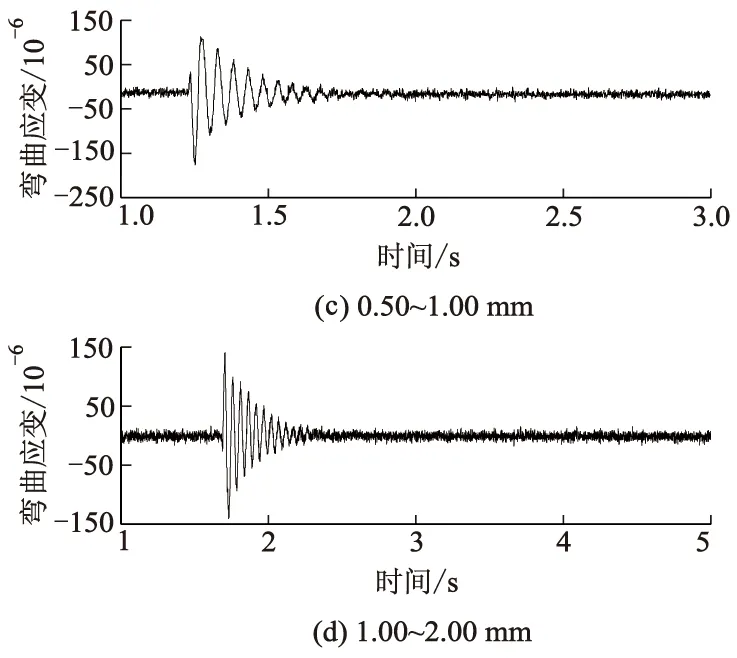
图12 距桩底15 cm处,桩径为20 mm的桩身应变时程图

图13 不同粒径范围下应变峰值随径径比值变化的曲线

3 结 论

1) 随着砂土粒径的增大,桩顶加速度幅值明显减小,桩体振动衰减时间有小幅变短．较其他粒径范围情形而言，大粒径范围(1.00～2.00 mm)下加速度峰值随径径比值增大的变化趋势线具有更大的斜率，即大粒径范围下，桩顶加速度对径径比值的变化更为敏感.

2) 在加速度频域范围内,同一桩径下,不同粒径范围的低频响应较丰富,随着砂土平均粒径的变化,傅里叶谱峰值也有不同程度的变化,但谱峰对应的频率变化不大．

3) 同一桩径下,随着砂土粒径的增大,桩身弯曲应变减小,桩身应变衰减变快,砂土粒径为0.10～0.25 mm时桩体恢复原始状态所需的时间最长．因此,砂土粒径是影响桩身应变的重要因素．